腹板倾斜角度对连续－刚构组合梁桥剪力滞效应的影响

冯 电，王浩之，谢文昌

(长沙理工大学桥梁与结构工程学院，湖南 长沙 410004)

目前大跨度梁式桥普遍采用长悬臂宽箱截面，以减轻自重和方便施工。这种截面剪力滞效应不容忽视。相对其它荷载而言，大跨度梁桥恒载产生的内力占总设计内力的80%～90%［1］，笔者抓住恒载效应这个主要因素分析了不同腹板倾斜角度对宽箱梁纵向应力和剪力滞效应的影响。长期以来，有大量学者对影响箱梁应力和剪力滞的梁高比、横隔板、结构横坡、顶底板以及腹板厚度等几何因素进行了研究，2010年Kumar［2］以箱梁的几何尺寸作为研究参数，建立了矩形和梯形截面的不同高跨比的几何非线性空间有限元模型，对恒载作用下的预应力混凝土箱梁剪力滞进行了分析，同年，Zou［3］等建立了44 片采用FRP 混凝土桥面板简支梁空间有限元模型，对FRP 混凝土桥面板的剪力滞进行了系统的参数分析。在国内，曹国辉等对影响薄壁箱梁的几何参数进行了系统的研究［4］，其中也涉及到了腹板倾斜角度对剪力滞效应的影响，但其针对的是等截面连续梁桥，截面为单箱单室，其结论对单箱多室的连续－ 钢构梁桥是否适应我们不得而知。张玉平等［5］通过改变顶底板、腹板厚度，对斜拉桥主梁剪力滞进行了几何参数分析，文献［6］对宽箱梁连续－刚构组合梁桥的剪力滞进行参数分析，其研究的参数主要包括宽跨比、翼板的宽度以及腹板的厚度。张杨永［7］在文献［6］的基础上研究了宽高比、跨径的布置对连续刚构桥剪力滞效应的影响。由于连续—刚构梁桥受多向约束效应的影响，空间受力复杂，使得其在成桥后顶底板出现不同程度的开裂，尤其是在零号块。因此，为了提高安全储备，准确分析连续—刚构组合梁桥的剪力滞效应是很有必要的。笔者以湘府路湘江大桥为背景，通过改变腹板倾斜角度，分析了腹板倾斜角度对连续—刚构组合梁桥关键截面剪力滞效应的影响，并得出可借鉴的结论。

1 工程背景

长沙市湘府路湘江大桥为南二环和南三环之间的唯一一座过江通道，主桥孔跨布置(见图1)为65 m+5 ×120 m+65 m，双向六车道，为连续—刚构组合体系，即Z3、Z4 号墩与主梁进行固结，而其它主墩与主梁之间的连接方式为铰接，主梁采用三向预应力变高度混凝土箱梁，截面为斜腹板(与底板成103°)单箱三室截面(见图2)，采用C55 混凝土，箱梁节段施工分0 号现浇段、1～13 号现浇段、边跨现浇段以及合拢段。其中0 号块长12.0 m，1～13号节段长度分别为3.5 m、4.0 m、4.5 m，次边跨、次中跨、中跨合拢段长2.0 m，采用导梁法施工。最重的悬臂浇筑段为1 号节段，其重量为3 964.4 kN。支点处梁高700 cm，跨中和边墩处梁高为300 cm，梁底曲线按二次抛物线变化，箱梁顶结构宽3 220 cm，箱梁底宽随梁高变化，由主墩处的1 938.6 cm 变化至跨中的2 120 cm。箱梁外侧悬臂长为500 cm，端部厚18 cm，根部厚65 cm。顶板厚度为28 cm，底板厚度由30 cm 变化至150 cm。腹板由支点至跨中分三段变化，厚度变化为50～85 cm。

图1 主桥立面图(单位:m)

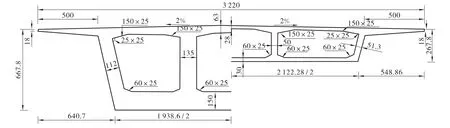
图2 横截面布置图(单位:cm)

2 有限元模型的建立

由于长沙市湘府路湘江大桥采用的是单箱三室箱形梁的结构形式，而箱梁受弯扭组合、剪力滞以及畸变等因素的影响受力情况比较复杂，因此，三维杆系模型无法完全准确模拟箱梁的受力情况，尤其是零号块。为了准确得到宽箱梁的空间受力情况，在杆系模型的的基础上，建立了局部分析的三维实体模型。

2.1 全桥杆系模型的建立

利用Midas Civil 分别建立了腹板倾斜角度为90°、103°(设计值)、116°、130°的全桥有限元杆系模型，其余尺寸与设计值一致。腹板倾斜角度的改变采用顶板宽度的变化来完成。为了准确得出腹板倾斜角度对箱梁应力和剪力滞的影响规律，在本桥模拟过程中只考虑桥梁自重载和二期恒载的作用(见表1)，全桥共划分了231 个节点和230 个单元(见图3)。

表1 二期恒载 (kN·m －1)

图3 湘府路大桥全桥有限元模型图

2.2 空间局部实体模型的建立

为了较为准确的分析跨中和墩梁固结处截面的应力分布情况，将湘府路大桥全桥的一部分(如图4)分离出来(包括了零号块和跨中部分)，利用Midas FEA 建立了这一部分的三维实体模型(包括4种不同的角度)，由圣维南原理可知，零号块和跨中结构的应力只与其附近范围内的应力状态有关，而远离的区域对其影响较小，一般可以忽略不计。为了避免应力集中，将其附近的4 个梁段也一并建出，并在两端加边界条件。力和位移的边界条件从Midas Civil 整体分析当中提取。由于箱梁截面比较复杂以及为避免某些单元在计算时卡死等现象，在网格划分时，采用Midas FEA 中的自动实体网格划分，划分长度人为的取为0.25 m。本模型的网格划分如图5所示。

图4 局部分析梁段

图5 局部分析模型

3 计算结果与分析

图6 不同腹板倾斜角度纵向应力云图

图7 墩梁固结部箱梁截面顶板纵向应力分布曲线与剪力滞系数曲线

图8 墩梁固结部箱梁截面底板纵向应力分布曲线与剪力滞系数曲线

图6为不同腹板倾斜角度下局部分析模型纵向应力云图，为了了解不同腹板倾斜角度下连续—刚构组合体系梁桥在恒载工况下关键截面的正应力以及剪力滞效应的变化情况，将关键截面纵向应力以及剪力滞系数分别绘制于各图，见图7～图10。其中图7、图8分别为墩梁固结处截面顶板和底板的正应力和剪力滞系数分布图，其横轴分别表示顶、底板的宽度，竖轴分别表示正应力值和剪力滞系数。图9、图10分别为跨中截面顶底板纵向应力和剪力滞系数的分布曲线，其横轴和竖轴意义同图7、图8。

由图7～图10可知，腹板倾斜角度的变化对不同截面顶、底板正应力和剪力滞效应影响程度不同。在墩梁固结部位和主跨L/2 处截面，腹板倾斜角度对顶板纵向应力影响较大，有些计算节点(不同模型的相同节点)的应力差值达到了1 MPa，对底板而言，其影响相对比较小(见图7a～图10a);腹板倾斜角度的变化对墩梁固结处截面顶、底板的剪力滞系数差值比较大，其最大差值达到10%(见图7b、图8b)，对于主跨L/2 处截面顶、底板腹板影响比较小，其剪力滞系数分布曲线基本是重合的(见图9b、图10b)。

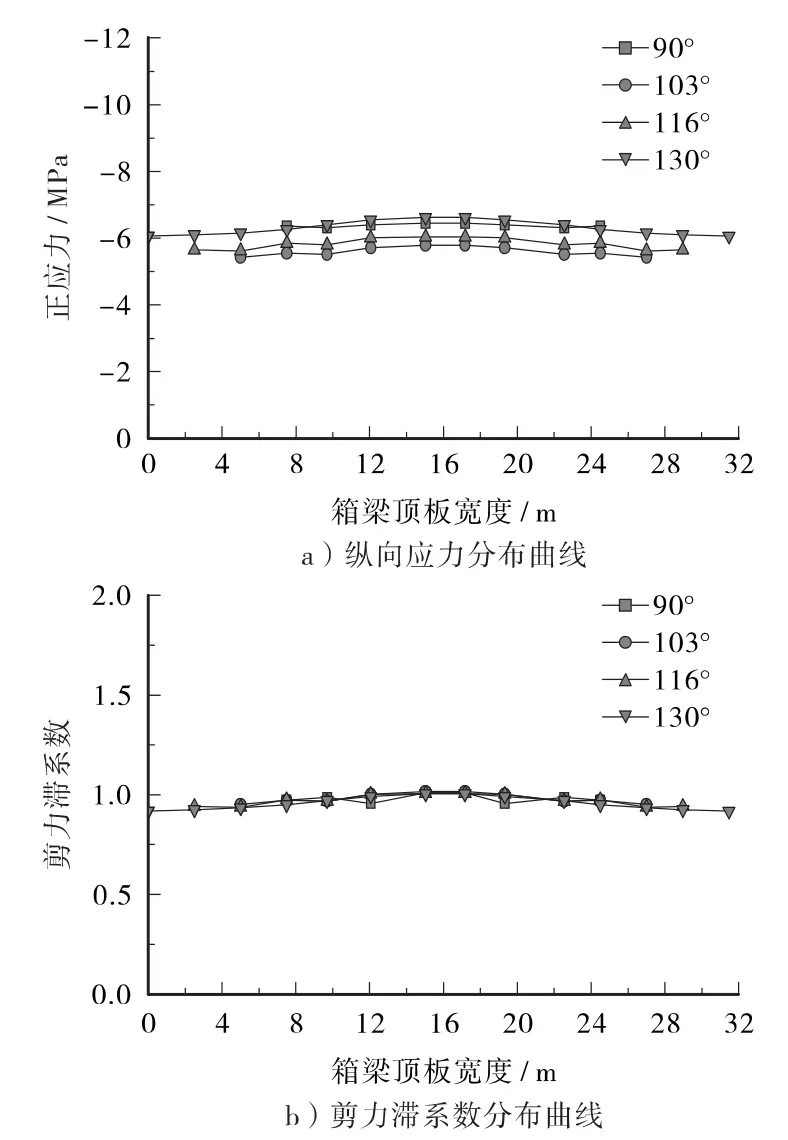
图9 主跨L/2 箱梁截面顶板纵向应力分布曲线与剪力滞系数曲线

图10 主跨L/2 箱梁截面底板纵向应力分布曲线与剪力滞系数曲线

4 主要结论

本文应用Midas Civil 和Midas FEA 建立了湘府路湘江大桥成桥阶段的全桥杆系模型以及三维局部实体模型，分析了不同腹板倾斜角度对连续—刚构组合梁桥关键截面纵向应力和剪力滞效应的影响，得出了以下结论:

1)腹板倾斜角度的变化对顶板的纵向应力影响比较大，对底板的影响相对较小。

2)腹板倾斜角度对连续—刚构组合梁桥墩梁固结处顶、底板剪力滞效应影响比较大，而对主跨L/2处截面顶、底板的影响较小，其剪力滞系数分布曲线基本是重合的。

3)由于实际结构与理想模型存在一定的差别，所以分析结果只能从整体上反映腹板倾斜角度对正应力和剪力滞效应的影响。

［1］李立峰，邵旭东，程翔云，等.变截面长悬臂宽箱梁桥翼缘有效宽度研究［J］.重庆交通学院学报，2004(2):1 －5.

［2］Kumar M.Influence of box-geometry onshear lag in RC box-girder bridges［J］.IndianConcrete Journal，2010，84(1):15－20.

［3］Bin Zou，An Chen，Julio F.Davalos，Hani A.Salim.Evaluation of effective flange width by shear lag model for orthotropic FRP bridge decks［J］.Composite Structures，2010.

［4］曹国辉，方 志，周先雁，等.影响薄壁箱梁剪力滞系数的几何参数分析［J］.中外公路，2003(1):39 －41.

［5］张玉平，李传习.顶板、底板和斜腹板厚度对斜拉桥箱梁剪力滞效应的影响［J］.长沙交通学院学报，2008(2):23 －28.

［6］何立平，张 涛.宽箱梁连续刚构桥剪力滞效应研究［J］.西部交通科技，2010(S1):82 －86.

［7］张杨永.连续刚构箱梁桥剪力滞效应的参数分析［J］.公路工程，2008(4):58 －60，66.