含DG的基于改进遗传算法的配电网重构
2014-05-28羿应棋
羿应棋
(三峡大学,湖北 宜昌 443000)
1 引言
分布式电源[1](Distributed Generation,DG)作为集中供电方式的一种补充,在充分利用可再生能源及减少环境污染等方面将发挥重要的作用,被誉为21世纪电力发展的关键技术。
配电网重构作为配电网优化运行的一种手段,在网络结构变化的情况下,可用来消除过载、降低网损,以及平衡各馈线的负荷,实现配电网可靠经济地运行网络重构是一个复杂的大规模非线性整数组合优化过程,在引入DG后,配电网络的拓扑结构会发生显著变化[1,2],因此研究含配电网的重构是非常重要和有意义的。
国内外关于配电网重构的研究较多,主要围绕重构算法展开。就目前而言,比较流行的一类重构算法是人工智能算法,其中主要包括模拟退火法(SA)[3]、禁忌搜寻法(TS)[4]、专家系统法(ES)[5]、蚁群优化算法 (ACO)[6]、免 疫 算 法 (IA)[7]、人 工 神 经 网 络(ANN)[8]和遗传算法(GA)[9]然而考虑 DG 对重构的影响的研究目前并不多见。
本文考虑了DG对配电网重构相关方面的影响,在正常运行情况下,以网络损耗为目标函数,采用改进的遗传算法编码策略,避免了在GA运行过程中产出大量不可行解从而导致计算效率较低,收敛特性较差。
2 DG对配电网重构的影响
按重构时系统的状态,可将配电网络分为事故重构和运行重构在DG大量接入配电网以后,将对配电网的重构策略带来深刻影响:一是遇到故障时,需要通过开关重置隔离故障,在不影响系统正常运行的情况下,形成有意识的孤岛[1]继续给部分用户供电,提高供电可靠性;二是在正常运行的情况下,为减少网损,提高经济性,对配电网进行重构时又应尽量避免孤岛的发生这是因为在系统与GA均带电时,突然的解列和下次并网都会给GA带来一定程度的冲击然而在正常运行状况下,出现的无意识GA孤岛(亦称非计划孤岛)将会产生诸多不利影响,如:会引起孤岛内频率和电压的变化,以及系统功率的不平衡,难以保证电能质量;由于非计划孤岛的范围不确定,会对维修人员运行人员及公众的安全造成威胁;形成孤岛运行后,与主系统配合不当,会引起不必要的停电损失因此,出于用电安全和用电质量的考虑,在正常运行时,应防止GA的非计划孤岛运行。
3 含DG的配电网重构数学模型
3.1 目标函数
配电网系统中一般有联络开关和分段开关两种类型,重构的主要任务是确定配电网中需要闭合的联络开关和需要打开的分段开关,以使最终的系统网损最小,因此本文选取配电网总线损最小作为目标函数,可以表示为:

由于在系统正常运行时各节点电压均在其额定值附近波动,其标幺值近似为1.0,所以本文在计算时各节点的电压标幺值均取为1.0,即目标函数中V*k的值为1.0,则系统的目标函数可简化为:
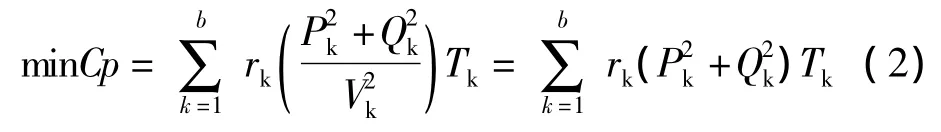
式中,b为支路数;Pk、Qk为支路k末端流过的有功功率和无功功率;rk为支路k的等效电阻。Tk为支路k上的开关状态,Tk=0表示开,Tk=1表示关。
3.2 约束条件
在进行配电网重构过程中,需要考虑如下约束条件根据配电网自身运行的特点,配电网络重构还必须满足以下约束条件。
(1)潮流约束

式中,Pi、Qi分别为节点i注入有功功率和无功功率的不平衡量;n为节点数;Vi、Vj分别为节点i和节点j电压的幅值;Gij、Bij分别为节点导纳阵的第i行、第j列元素的实部和虚部;δij为节点i、j电压的相角差。
(2)电压约束

式中,Vmini、Vmaxi分别为节点i电压幅值的上、下限。
(3)容量约束

式中,Sk为支路k的功率;Smaxk为支路k的功率上限。
(4)辐射状运行约束

式中,gl为当前的网络结构;Gl为所有允许的辐射状网络结构。为了保证配电网的辐射状运行,在开关的开/合过程中必须考虑如何限制形成所谓的环和孤岛问题。
此外,系统中开关动作的次数或数量过多,对一个配电网的运行及开关的使用寿命也是不经济的,所以需尽量减少开关的动作次数和数量。
4 改进遗传算法在含DG的配电网重构中的应用
遗传算法(GA)具有并行计算特性与自适应搜索能力,并且可以在一个大规模、多极值点且具有不确定性的解空间中进行全局优化搜索。所以,近些年来遗传算法已经广泛的应用于电力系统的配电网重构中了。
4.1 改进遗传算法的编码策略
传统GA将网络中开关的状态用0和1表示每个开关占据染色体的1位,0代表分闸状态,1代表合闸状态,各支路状态组合在一起就形成了一条染色体,染色体的长度为网络中开关的数目。但这种编码方法没有考虑到配电网结构的具体情况,在GA的运行过程中会产生大量的不可行解,严重影响了GA的计算效率。
改进遗传算法在编码过程中主要考虑了以下两个方面的改进因素:
第一:由于配电网在运行过程中不能形成环和孤岛,其中孤岛包括节点孤岛和电源孤岛,所以在配电网中一般要保证与电源相连的支路必须保持连通,而仅有唯一一条支路供电的节点,其供电支路也必须保持连通。所以根据以上规定在遗传算法编码过程中可以将这些必须保持连通的支路所对应的位从染色体中消除。经过上述简化处理,染色体长度可以大大缩短,从而使搜索空间可行解的比例提高。
第二:在配电网中一联络开关对应一环路,在编码过程中可以将构成同一环路的开关放在在同一基因块内、相邻开关在染色体中相邻的染色体编码策略,这样采用交叉操作只进行对应基因块的交换,而将变异和逆转操作限制在基因块内的遗传操作策略,则只有变异操作可能产生不可行解,但可以通过特殊操作将不可行解消除。
4.2 产生初始种群
初始种群的产生步骤为:首先根据编码规则,随机产生一个编码向量;然后判断编码向量所确定的网络结构是否满足配电网辐射状运行约束,若满足要求,则将其选为初始群体的染色体;最后重复以上步骤,直至产生初始种群数量P。
4.3 改进遗传算法的基因操作
(1)交叉操作
GA的交叉操作是指把2个父辈染色体中的部分结构交换重组而生成新个体的操作。对于一个16节点,具有3个环路的配电网,可以先以环为单位将染色体分为3块,每次交叉操作只将对应块的基因进行交换。首先,产生一个1~3之间的随机数,通过随机数来确定需要进行交换的基因块,如产生的随机数为2,则将父辈染色体中的第2个基因块进行交换。如:
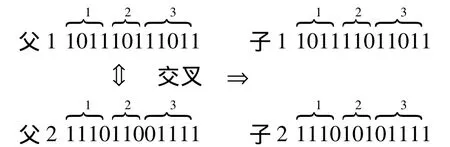
(2)变异操作
变异操作就是把某些基因座上的基因值取反。首先选定一基因块,然后在确定的基因块中随机选定一位基因将其值取反。进行变异操作后将产生不可行解,需要将产生的不可行解消除。如变异操作将1变为0,则将基因块内变异位前为0的一个位置变为1;如变异操作将0变为1,则将其后一位基因(在同一基因块内)变为0;从而保证变异操作没有不可行解产生。如:

(3)逆转操作
逆转操作为变异操作的一种特殊形式,其操作为任意选定的一个基因块,然后将基因块中的基因值以逆转概率逆向排序,逆转操作在基因块中进行无不可行解产生。如:

通过以上改进的交叉、变异操作,与传统遗传算法相比可以大幅度的提高GA的搜索效率以及收敛速度。
4.4 终止判据
由于当种群均值与种群中最优解的值保持一致超过代时,则可以认为算法已经收敛,因此可以将上述条件作为收敛判据,即满足该条件时,则过程结束,输出最优解,若不满足则继续迭代。
5 算例分析
本文研究含DG的配电网重构,对IEEE 3母线16节点配电系统进行了改进,各支路的连接情况如图1所示,研究中各支路的阻抗以及负荷如表1所示。
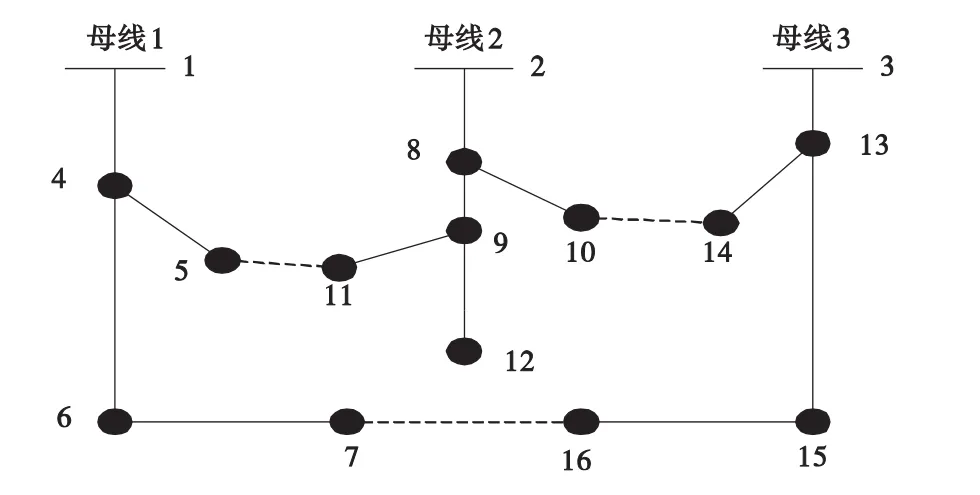
图1 IEEE 3母线16节点系统结构图
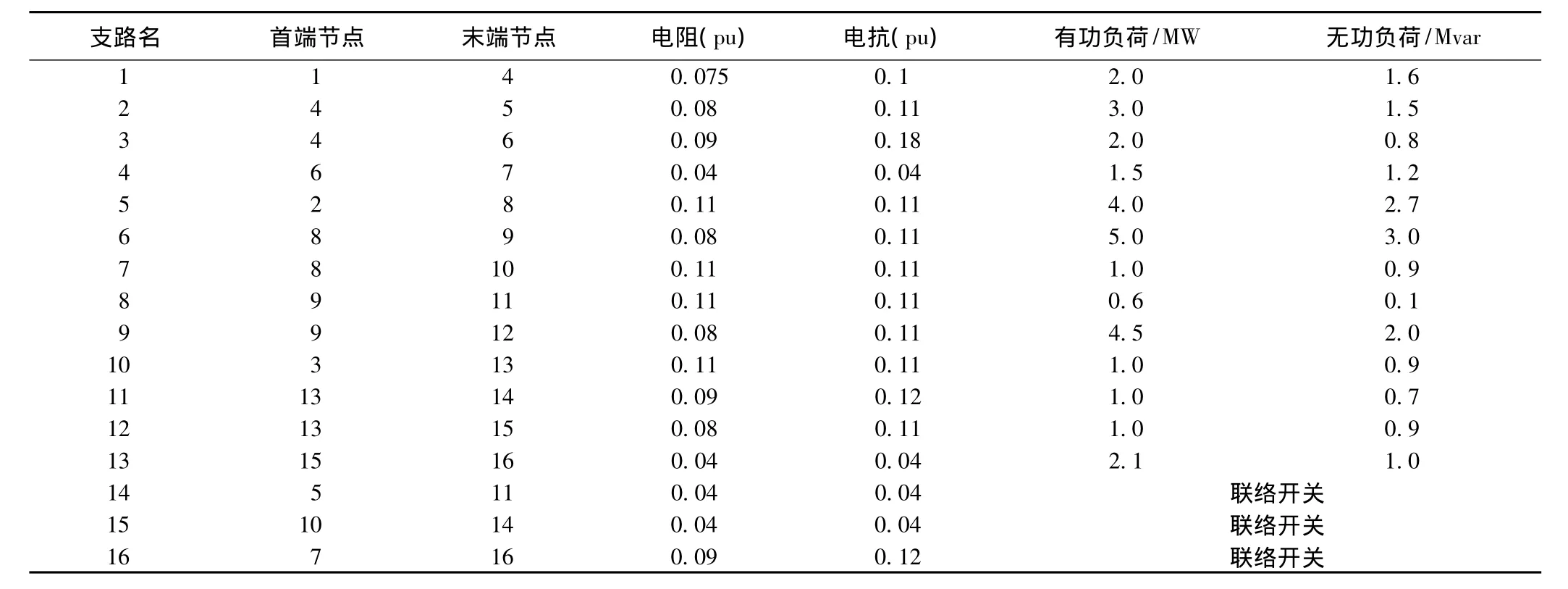
表1 IEEE 3母线16节点系统参数表
该系统的总负荷为:(28.7+j17.3),系统基准容量为100,额定电压为10kV,其中节点6和12节点分别作为DG的接入点。
采用近似的潮流计算法及改进GA法,利用Matlab语言编制了配电网重构的优化程序,对图1设计了5种重构方案,包括含有DG和不含DG两种情况。其中,种群数量 P=20,交叉概率 Pc=0.9,变异概率Pm=0.1,逆转概率Pl=0.5,终止判据中N=2。
(1)不计及DG。
(2)计及单个DG,在节点12注入容量为的DG。
(3)注入不同容量的DG,在节点12注入容量为(2.0+j 0.5)的DG。其收敛特性图如图2所示。
(4)在不同节点注入DG,在节点6注入容量为(1.0+j 0.5)MV·A的DG。
(5)计及多个DG,分别在节点12与节点6注入容量(1.0+j 0.5)MV·A的DG。
对于以上5种方案进行了分析比较,各开关状态与网络损耗如表2所示。

图2 改进遗传算法收敛特性图
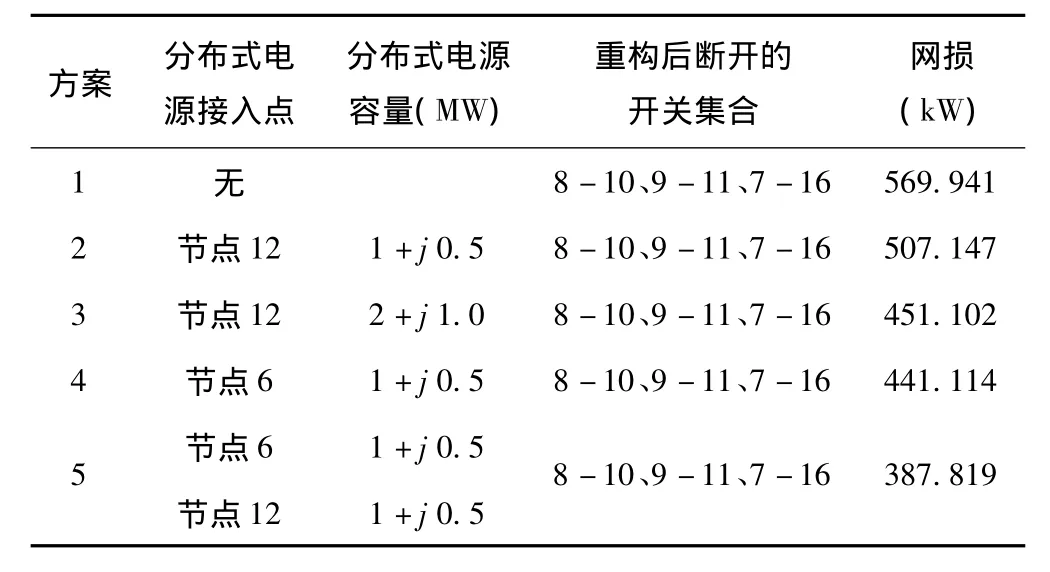
表2 各方案的重构结果
分析以上方案设置及计算结果,可知:
(1)与未接入DG相比,DG接入配电网后的各种方案,在开关设置合理时,能够减小配电网络的有功损耗,这说明的注入对降低网损起到了积极作用。
(2)比较方案2,方案3,方案5,发现DG并网后的网络损耗随并网位置及容量的不同而变化。
(3)在接入配电网总容量相同的情况下,分散DG接入对降低网损的效果更为明显。
(4)多DG接入更能发挥平衡负荷作用,改善了网络运行结构,也降低了系统的网络损耗,从而使系统最优化运行。
(5)由方案3的改进GA的收敛特性图可以看出,在进行到9代时已接近收敛,其收敛速度较快。
6 结论
(1)DG接入配电网在一定程度上对降低配电网络损耗有积极作用,同DG的容量及位置不同,对配电网的影响也不同,规划时寻求合理的DG接入方案对配电网的运行及DG效益的发挥有重要意义。
(2)通过改进的编码的方式能够很好的避免了传统遗传算法在运算过程中产生大量的不可行解,从而提高了算法的搜索效率以及收敛速度。
[1]IEEE Std 1547.Standard for interconnecting distributed resources with electric power systems[C]//IEEE Standards 23 - 26 Coordinating Committee 21,2003:3 -12.
[2]韦钢,吴伟力,胡丹云.分布式电源及其并网时对电网的影响[J].高电压技术,2007,33(1):36 -40.
[3]Hong-Chan Chang,Cheng-Chien Kuo.Network reconfiguration in distribution systems using simulated annealing[J].Electric Power Systems Research,1994,29(3):227 -238.
[4]Thakur T.Application of Tabu-search algorithm for network reconfiguration in radial distribution system[C]//International Conference on Power Electronics,Drives and Energy Systems,2006:1 -4.
[5]Aoki K,Kuwabara H,Satoh T,et al.An efficient algorithm for loadbalancing of transformers and feeders by switch operation in large scale distribution systems[J].IEEE Transactions on Power Delivery,1988,3(4):1865 -1872.
[6]Xiong N,Cheng HZ,Yao LZ.Switch group based Tabu search algorithm for distribution network reconfiguration[C]//Third International Conference on ElectricUtility Deregulation and Restructuring and Power Technologies,2008:820 -822.
[7]Lin CH,Chen CS,Wu CJ.Feeder reconfiguration for distribution system contingencies with immune algorithm[C]//IEEE Porto Power Tech Conference,2001(3):6 -12.
[8]KIMH,KOY,JUNG K H.Artificial neural-network based feeder reconfiguration for loss reduction in distribution systems[J].IEEE Transactions on Power Delivery,1993,8(3):1356 -1366.
[9]Nara K,Shiose A,Kitagawa M.Implementation of genetic algorithm for distribution systems loss minimum re-configuration[J].IEEE Transactions on Power Systems,1992,7(3):1041 -1050.
[10]徐兴华,刘伟.配电网重构的研究与展望[J].山东电力高等专科学校学报,2000,7(3):23 -30.
[11]张大海,江世芳,赵建国.配电网重构研究的现状与展望[J].电力自动化设备,2002,8(2):55 -60.
[12]毕鹏翔,刘健,张文元.配电网络重构的改进支路交换法[J].中国电机工程学报,2001,21(8):98 -103.
[13]吴本悦,赵登福,刘云,等.一种新的配电网络重构最优流模式算法[J].西安交通大学学报,1999,33(4):22 -24.
