区间不确定集鲁棒优化的含风电系统无功电压控制

杨雨薇，温智慧，徐晟

(1.国网湖南省电力公司培训中心，湖南 长沙 410131;2.国网长沙供电公司，湖南 长沙410000)

1 引言

随着风电场并网容量的增加，由于输出功率与风速变化日益密切，含风电场的整个系统的有功功率和无功功率将产生波动［1］。同时电压稳定问题日益受到重视，出现了风电场随风速增加导致母线电压崩溃的现象和系统运行方式变化导致母线电压波动［2］致使风电机组停机的情况。因此，为了保证风电场接入后系统仍安全稳定运行，必须降低全网有功损耗且提高系统电压水平，优化全网无功分布，解决变化风速所带来的无功电压控制问题。

无功电压控制是指在系统结构参数以及负荷情况给定，且满足所有约束条件的前提下，使系统某一个或多个指标(如全网有功损耗最小、电压质量最优、年费用最少等)达到最优的非线性规划问题［3］。含风电系统无功电压控制问题涉及风速的不确定性，是一个含有随机参数的、离散的、带约束非线性组合优化问题。

在研究含风电系统无功电压控制问题时，较少文献选取随机性的风速作为随机变量。普遍以风电场在恒功率因数运行情况下求得其并网点处无功补偿容量，在满足风电场无功补偿的前提下，建立以全网的有功网损最小为目标函数的无功电压控制模型并求得最优解［4］。现有的文献中提出风电场无功的随机变化影响平均电压水平和风电场甚至局部区域电网的潮流分布［5］，着眼于风电场并网运行引起的电压稳定和风电场内部功率损耗的问题，以风力发电机模型较准确地描述了其有功和无功之间的关系，并且考虑了风速的变化对风力发电机出力的影响［4－6］，而对于风电场接入电网后整个系统的无功电压控制问题未进行探讨［7］。通过将具有随机性的风电机组输出功率划分可能发生的场景，考虑场景发生的概率并引入一种基于场景发生概率的无功优化综合指标，该指标综合考虑网损和静态电压稳定裕度两部分，提出一种基于该指标的配网无功优化模型［8］。将风电场作为出力呈间歇性的发电来源之一，可以通过粒子群优化算法解决风电接入系统的无功电压控制问题，确保可再生能源成功接入电网［6］。文献［9］对风速进行蒙特卡罗仿真，建立了包含分布式发电的配电网无功电压控制模型。文献［10］以双馈型风电机组为研究对象，建立以风电无功功率、并联电容器投运组数为优化变量，以电压偏差最小和有功网损最小为目标的无功电压控制模型。

但以上大都采用确定性规划方法，未能计入风电出力随机性。因此，假设风速服从 Weibull分布［8，9］，以输电线路的功率传输极限、常规机组的出力约束为主要约束条件。然而对风电场的随机性需要考虑不确定性参数的概率分布，但是其分布函数往往很难得到准确表达。

鲁棒优化是从计算复杂性的角度研究不确定优化模型鲁棒最优解的数学方法［11］，也是一种建模方法，通过计算工具来解决模型中含有不确定数据或者仅仅知道其属于某一个不确定区域的优化问题［14］。本文提出了用鲁棒优化理论建立一个含风速不确定性的计算全网损耗最优的数学优化模型，该模型不需要知道风速的随机分布函数，采用区间不确定集来表示风速的不确定性，运用优化对偶理论进行化简，使得模型中的不确定量转化为确定的形式，从而便于求解优化结果。

2 接入风电场节点的无功出力处理

2.1 风电场输出功率计算

由于风速具有波动性，风电场输出有功则具有随机性。得到风电机组输出功率与变化风速之间的关系，即式(1):

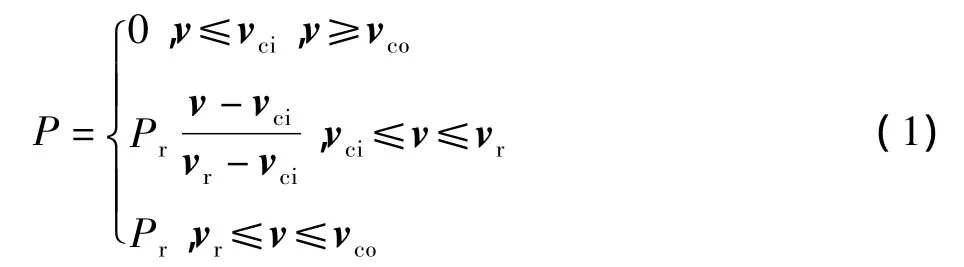
其中，Pr为风机额定输出功率;vci为风机切入风速，大于此值并且小于额定风速时风电机组处于欠额定运行状态，对应的有功输出介于零和额定值之间，具体值与风速大小有关;vr为额定风速，风电机组处于额定运行状态;vco为切出风速，大于此值时风电机组停机退出运行，输出功率为零。

2.2 接入风电场节点的无功功率

一般风电场的输出功率为所有风电机组功率之和。假定风电场以恒定功率因素运行，风电场带并联电容器运行。当风速已知，有功确定，风电场以某一功率因数运行，风电场出口的无功功率［4］为:

其中φ为风电场的功率因数角。由于风力发电机通常是异步发电机，所以φ为负值，P是风电场有功出力。故接入风电场节点的无功功率为:

其中，QC为风电场无功补偿容量。

从上面的关系式可以看出接入风电场节点的无功功率在数值上等于风电场出口无功功率与风电场无功补偿容量之间差值。

3 区间不确定集合下鲁棒优化模型

3.1 鲁棒优化基本模型

鲁棒优化与随机规划不同之处在于不需要已知不确定参数的随机分布，而是假设不确定参数属于一个有界的不确定集合。鲁棒优化解决内部结构含有不确定情况的问题时，对于数学规划问题而言，一种是约束条件中参数的不确定性，一种是目标函数中参数的不确定性［13，14］。

一般的鲁棒优化模型如下:

这里x为决策变量，ξ为不确定的量，U就是一个不确定集［13］。

线性规划定义如下:

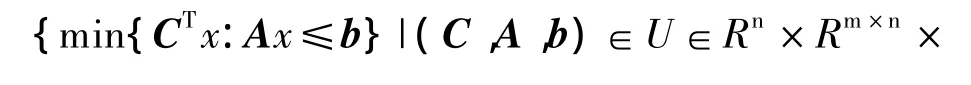
记 A={ai，a2，…，am}T，b={b1，b2，…，bm}T其中ai为约束矩阵A的第i行，则式(5)可写为如下形式

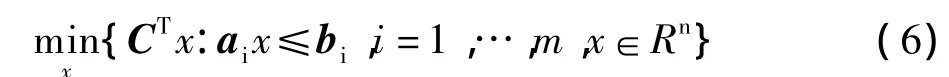
假设 a1∈U1，a2∈U2，…，am∈Um，其 Ui，i=1，…，m为不确定集合，则式(6)对应的鲁棒优化模型如下:

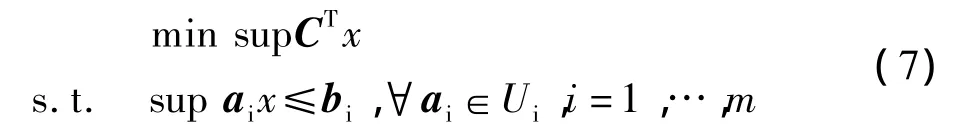
优化模型(7)中的 aix≤bi，∀ai∈Ui，i=1，…，m可等价于求解以下问题:

3.2 区间不确定集

鲁棒优化在处理时的关键问题是不确定集合U的确定，以及如何在给定U的情况下对复杂模型的化简［11－14］。不确定集合U可以取椭圆不确定集或区间不确定集。考虑到实际计算的可操作性，本文采用区间不确定集且其具有下面的结构:

式(9)中的e表示元素为1的列向量，ξ－和¯ξ是给定的量。在具体的鲁棒线性优化模型中ξ表示的是不确定量的扰动范围。

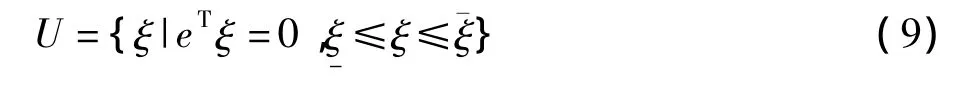
4 求解含风电系统无功电压控制数学模型

4.1 含风电系统无功电压控制

系统无功电压控制是在满足系统运行约束的条件下，稳定节点电压并使系统的有功网损最小，优化风电场无功补偿容量及系统无功分布。其数学模型为:

(1)目标函数:

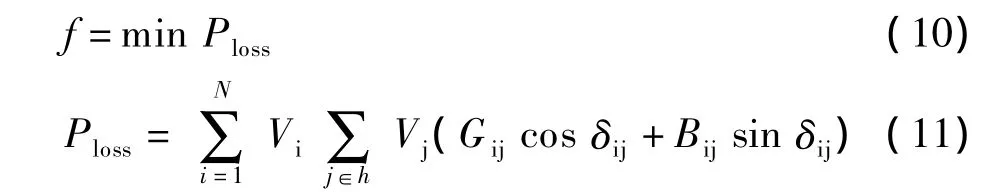
Ploss为系统有功网损;

(2)等式约束:

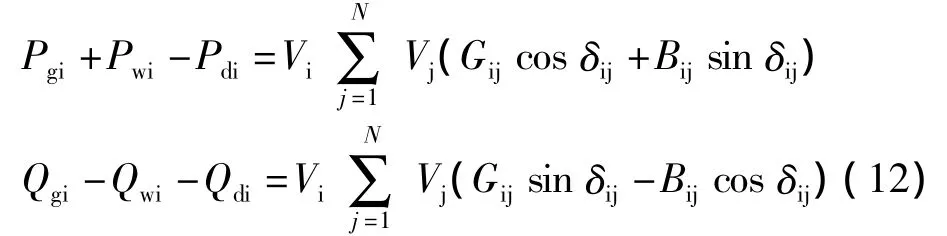
式中:N为电网节点总数;Pgi，Pdi分别为节点的有功注入和有功负荷;Qgi，Qdi分别为节点i的无功注入及无功负荷;Pwi为风电场发出有功功率;Qwi为风电场吸收无功;Vi，Vj，Gij，Bij，ξij分别为节点 i和 j的节点电压，节点i和j之间的电导、电纳及电压相角差。

(3)不等式约束:式中:Vi，QGi表示节点的电压和发电机节点的无功。

4.2 含风电场电力系统无功电压控制模型

在含风电场的电力系统中，以求得系统有功网损最小作为优化目标，将节点电压上下限、发电机无功出力上下限为不等式约束，把系统的无功功率平衡方程作为等式约束［16－17］。则前面的含风电场电力系统无功电压控制模型可表示为:

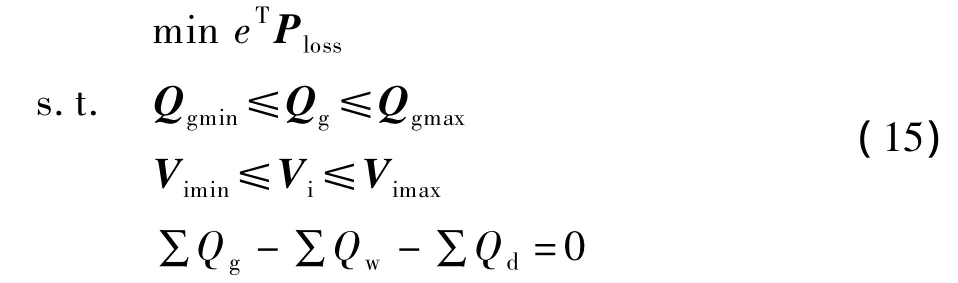
Ploss为含风电场的电力系统有功功率损耗向量;eT为与Ploss同维且所有元素为1的列向量;Qg为常规发电机组的无功功率向量;Qgmin和Qgmax分别为常规发电机组无功出力的上下限向量;Qd为负荷的无功功率列向量，取正值;Qw为风电场的吸收无功功率列向量;Vi为节点电压向量;Vimin和Vimax为节点电压的上下限向量。

4.3 系统的电压/无功线性化关系

设含风电系统共n个节点，nPQ个PQ节点，风电场看作PQ节点，nPV个PV节点，一个平衡节点。在极坐标下，牛顿－拉夫逊潮流计算方程［15］得:

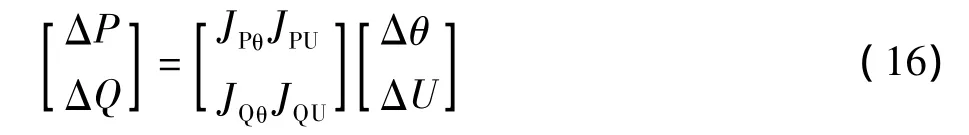
式中:ΔP为节点注入有功的微增列向量，有n－1个元素;ΔQ为节点注入无功的微增列向量，有nPQ个元素;Δθ为节点电压相角变化列向量，有n－1个元素;ΔU为节点电压幅值变化列向量，有nPQ个元素。是极坐标下的潮流方程Jacobi矩阵，其中JPθ为 ∂P/∂θ子阵;JPU为 ∂P/∂θ子阵;JQθ为 ∂Q/∂θ子阵;JQU为∂Q/∂U子阵。考虑到电压幅值与无功功率强耦合，在电压控制与稳定分析中常常不计有功的影响，只考虑无功和电压的关系。令有功注入保持不变，即ΔP=0，得

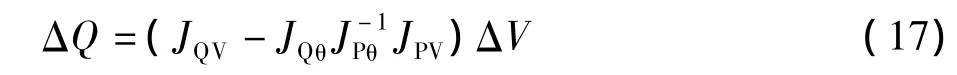
令(JQV－ JQθJ－1PθJPV)=JR，得 ΔQ=JRΔV。因此，得到系统的电压/无功线性化关系模型:

式中:J=J－1R为电压/无功灵敏度矩阵，体现系统节点电压与无功变化之间的关系。

4.4 区间不确定集下鲁棒优化模型

结合式(4)，需变换优化模型(15)中的节点电压不等式约束。则将(15)中的节点电压不等式约束化为:

δ根据具体对电压水平的要求而定，例如5%，10%。本文中选取5%。

即

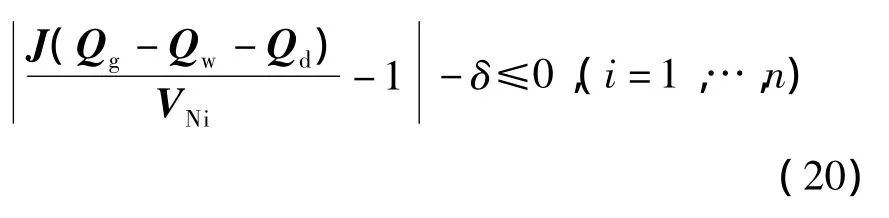
对所有支路而言，均需要满足(20)，只是式(20)左边部分数值大小不同。选择其中最大值所在的支路，如该支路也满足(20)，则所有支路均满足，所以不等式约束可写为:0，(i=1，…，n)

则将(15)变换为区间不确定集下鲁棒优化模型的形式:

其中，系统含 n 个节点，Qgi、Qwi、Qdi分别代表系统中第i个节点上的常规机组无功出力，风电场、负荷吸收无功功率。

U={ξ|eTξ=0，ξ－≤ξ≤¯ξ}

其中¯v为风电场接入地点的风速估计值;ξ为根据实际风况选定的风速扰动区间。

5 区间不确定集下鲁棒优化模型转变

由于约束条件中含有不确定参数，使得模型难于求解，于是目标为将模型(21)转化为含有确定量的形式。另外，因为等式约束在优化模型中不易处理，于是考虑将等式约束代入到不等式约束中。

令约束条件中式(21－b)中的－J/VNi=H，是一个L×(n－1)维的矩阵，则 H用列向量的形式表示V=(V1，V2，…，Vn－1)，则有

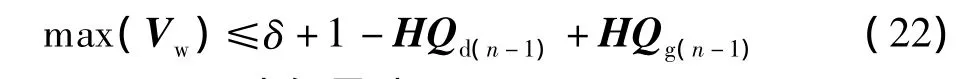
Qg(n－1)用列向量表示 Qgn=(Qg1，Qg2…Qgi…Qg(n－1))，根据无功功率平衡约束

于是可以得到:

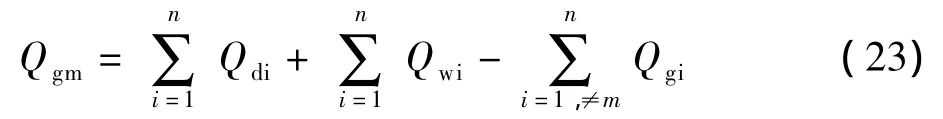
Qgm是第m个节点处的常规发电机组无功出力。考虑风电场接入系统中一个节点的情况，因此Qwi。于是有:

将式(24)代入式(22)则有

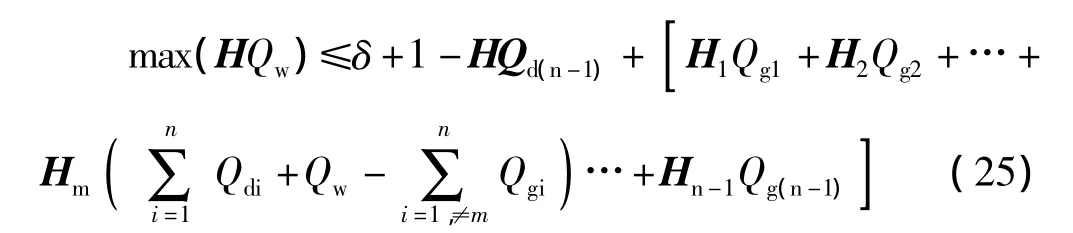
于是式子(22)最后变成下面的形式

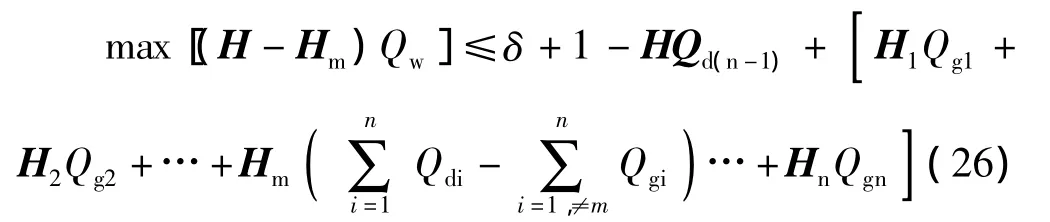
根据优化对偶定理，有

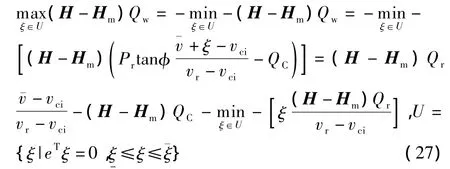
于是(26)转化成下面的形式

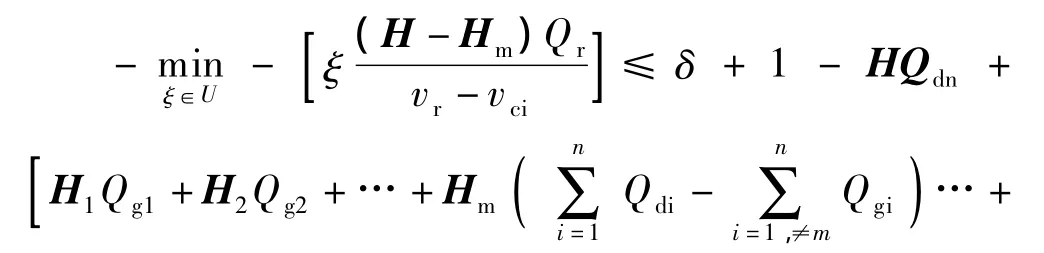
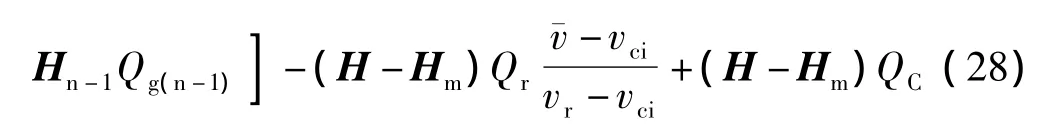
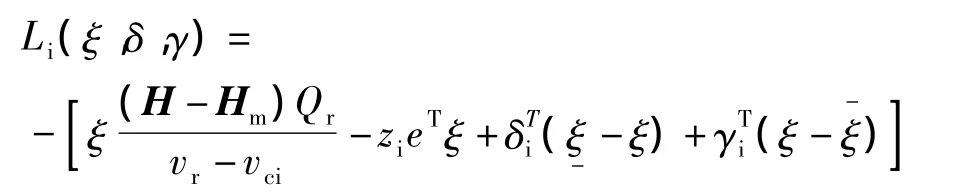
令▽ξLi(ξ，δ，γ)=，根据对偶定理:进一步得到:此时模型约束条件部分可以写成:

通过转化，可以从(29)看到模型已经化为一般的线性规划模型，于是借助软件MATLAB编写相关程序来求解满足约束条件下的含风电场的电力系统网损最小值以及系统平均电压水平。

6 算例与分析

为验证所提出的模型和算法的准确性，以风电场接入IEEE30节点系统进行仿真。利用Matlab7.0实现编程和计算。参与优化的各常规机组的无功出力上下限值如表1所示。

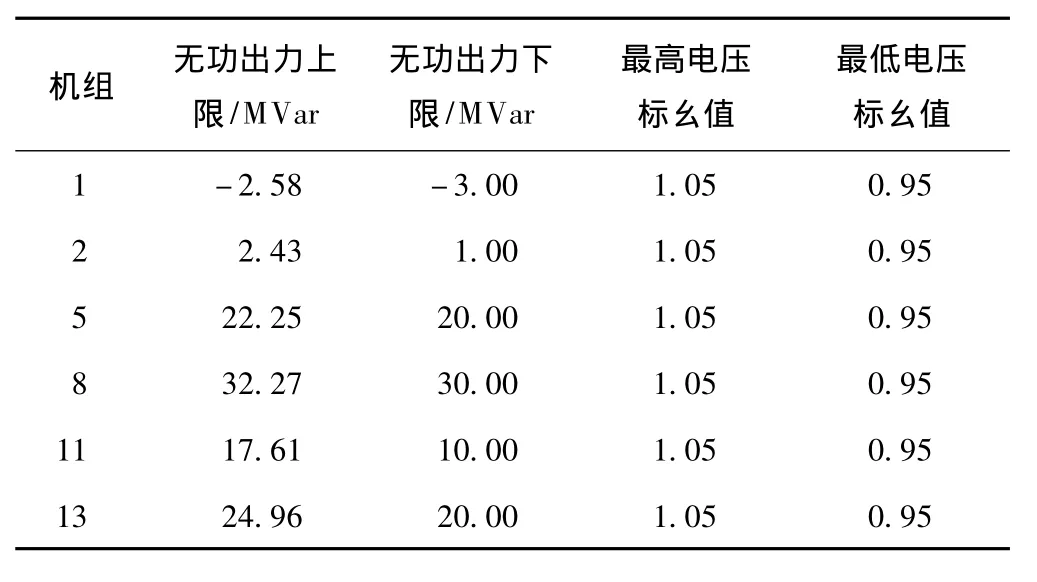
表1 IEEE30节点系统常规发电机组的无功出力上下限(MVar)

该系统的最大无功负荷为126.2MVar。为对比风电场从不同节点接入系统，不同的风速扰动范围、风机参数下求得的含风电场系统有功损耗最小值，分别选取风电场从节点16、18、20、25和30接入系统，设计了以下3个方案:

方案一:考虑风电场出力的随机性，在不同的扰动范围下，计算各个节点接入风机的系统网损，取额定风速15m/s，切入风速5m/s，切出风速25m/s，风速的估计值为10m/s，扰动范围为m/s，计算结果如表2所示。

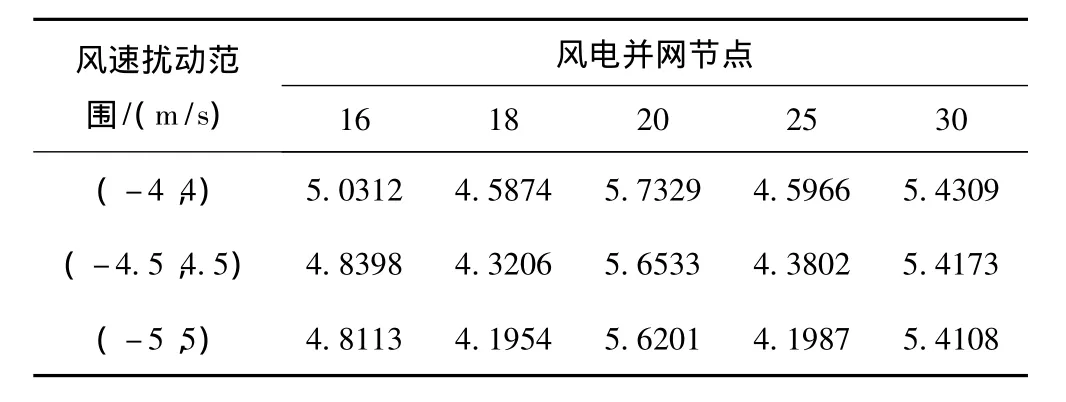
表2 方案1含风电场电力系统的系统网损结果(MVar)

方案二:取额定风速、切入风速和切出风速分别为13m/s、5m/s和 24m/s，风速的估计值为 10m/s，扰动范围为m/s，结果如表3所示。

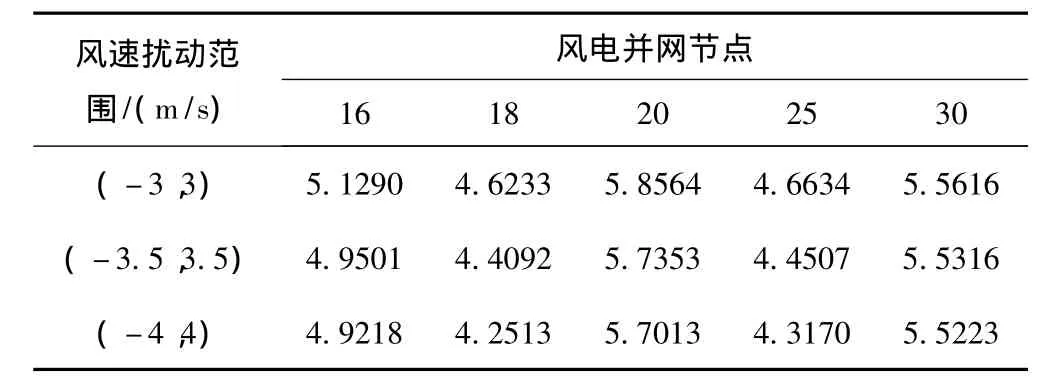
表3 方案2含风电场电力系统的有功网损结果(MVar)

方案三:不考虑风电场的随机性，计算风电场接入9节点的系统有功损耗以及系统平均电压，风机参数同上的取值，计算结果如表4、表5所示。

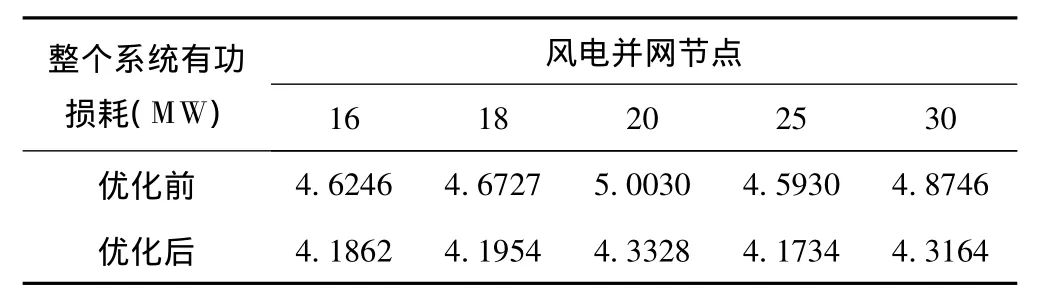
表4 方案3含风电系统的系统有功损耗结果

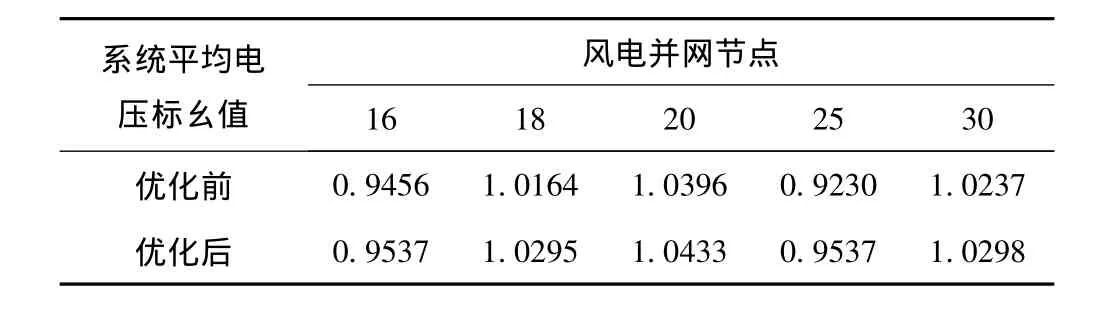
表5 方案3含风电系统的系统平均电压标幺值结果

由表4可以看出系统有功网损由优化前的4.6727MW降为优化后的4.1954MW，减少了0.4773MW(20%)。由表5可以看出，系统平均电压水平由1.0164(p.u.)提高到1.0295(p.u.)也有所提高。可以看出在不同的节点接入风电场，网损最小值有着明显的不同，这对于风电场规划人员的选址有着重要的参考意义。另外，从上表的变化趋势可以看出随着风速扰动范围的增大，系统总有功损耗是逐渐减小的，说明风速的变化范围越大，即风机的出力变化也比较大，则对系统运行方式的要求提高，即对其鲁棒性的要求也随之提高。

7 结论

本文采用鲁棒优化方法不需要知道风速的概率分布，而是将风速的不确定性以区间不确定集表示，通过对偶定理简化模型为一般线性模型，构建风电系统无功电压控制数学模型。通过分析IEEE30节点算例仿真结果表明风速的不确定性对风电系统无功分布有显著影响。风电场接入系统的不同节点以及风速的不同波动范围，不同风机参数等因素都影响全网有功损耗和电压水平。运用区间不确定集下鲁棒优化方法有效解决风电随机性使电网无功分布和电压水平改变的问题，降低系统有功损耗，提高电压水平，保证风电并网后系统的经济运行。

［1］Falck C J，Hatziargyriou N，Gruelund A S，et al.Methods and models for evaluating the impact of decentralized generation［C］.CIGRE38 －301，Paris，1998.

［2］张勇军，翟伟芳，林建熙.分布式发电并网的网损影响评价指标研究［J］.电力系统保护与控制，2011，39(13):134 －137.

［3］张勇军，翟伟芳，林建熙.分布式发电并网的网损影响评价指标研究［J］.电力系统保护与控制，2011，39(13):134 －137.

［4］胡敏，周任军，杨洪明，等.考虑风力发电的系统无功优化模型和算法［J］.长沙理工大学学报(自然科学版)，2009，6(1):43 －48.

［5］LI Ling，ZENG Xiangjun，ZHANG Ping.“Wind Farms Reactive Power Optimization Using Genetic/Tabu Hybrid Algorithm”，Proceedings of the IEEE Power System Technology，2002，26(8)Page(s):8 －11.

［6］程杉，陈民铀，黄薏宸.含分布式发电的配电网多目标无功优化策略研究［J］.电力系统保护与控制，2013，41(10):45 －50.

［7］陈树勇，申洪，张洋，等.基于遗传算法的风电场无功补偿及控制方法的研究［J］.中国电机工程学报，2005，25(8):1 －6.

［8］陈海焱，陈金富，段献忠.含风电机组的配网无功优化［J］.中国电机工程学报，2008，28(7):40 －45.

［9］魏希文，邱晓燕，李兴源，等.含风电场的电网多目标无功优化［J］.电力系统保护与控制，2010，38(17):107 －111.

［10］段建东，杨杉.基于改进差分进化法的含双馈型风电场的配电网无功优化［J］.电力自动化设备，2013(11).

［11］邓鹏华，刘颖，毕义明，等.鲁棒线性优化问题研究综述［J］，控制与决策，2009，24(8):1121 －1125.

［12］丁玉凤，文劲宇.基于改进PSO算法的电力系统无功优化研究［J］.电力系统保护与控制，2005，33(6):20 －24.

［13］王函韵，胡哗，朱卫东，等.信息不确定性对电网无功优化的影响［J］.中国电机工程学报，2005，25(13):24 －28.

［15］曾令全，王立娟.基于电压灵敏度的分布式发电最大渗透率的研究［J］.华东电力，2013，41(6):1175 －1179.

［16］周冬旭，李晓明.面向电力市场的含风电机组配电网无功优化模型及其求解算法［J］.电力自动化设备，2013，33(4):24 －29.

［17］Yuwei Yang，Renjun Zhou，Xiao Hong Ran.Robust Optimization with Box Set for Reactive Power Optimization in Wind Power Integrated System［C］.2012 IEEE Power and Energy Society General Meeting.San Diego，CA，2012:1 －6.