间断激励函数Hopfield神经网络解的存在性

潘玉峰

（晋中学院数学学院，山西 晋中 030600）

间断激励函数Hopfield神经网络解的存在性

潘玉峰

（晋中学院数学学院，山西 晋中 030600）

不考虑网络激励函数的有界性与单调性，本文对间断激励函数的神经网络进行了研究．通过Leray-Schauder选择定理和广义的Lyapunov方法，得到一个能够保证网络的解存在性的充分条件．

Hopfield神经网络；间断激励函数；Leray-Schauder选择定理

1 预备知识

设Rn为n维欧氏空间，Pf(c)（Rn）（Pk(c)（Rn））为Rn的非空闭凸（非空紧凸）子集的集合．设多值函数F∶T=［0,ω］→Pf（Rn）是可测的，如果对所有x∈Rn的-值函数t→d（x,F（t））=i nf｛‖x-υ‖∶υF（t ）｝是可测的．

设E⊂Rn．如果任意x∈E，存在非空的F（x）⊂Rn，则说映射x→F（x）是由E到Rn的集值映射；对x0∈E，如果任意开集N⊂F（x0），存在x0的开集M使得F（M）⊂N，就说集值映射F在x0处是上半连续的．

以下为Leray-Schauder选择定理：

引理1.1如果是一个巴拿赫空间C⊆X非空凸集，0∈C，G∶C→Pkc（C）为从有界集到相对紧集的丄半连续的集值映射，则下面结论有一条成立：

（1）集合Γ=｛x∈C∶x∈λG（x），λ∈（0,1）｝无界；

（2）G（·）有一个不动点，即存在x∈C使得x∈G（x）．

考虑以下H opf i el d神经网络模型：

其中，D=diag（d1,d2,…,dn）为对角矩阵，且di＞0，i=1,2,…,n.表示系统的自制系数；A=（aij）n×n表示连接权矩阵，aii＜0；g（x）=（g1（x1）,g2（x2）,…,gn（xn））为对角函数，表示网络输入输出的激励函数；I（t）=（I1（t1）,I2（t2）,…,In（t））T为以ω周期的向量函数，表示网络的外部输入．

在这里假设I（t）在T=［0,+∞］上连续．对激励函数满足以下假设：

（H1）gi在R的任意有限区间内至多有有限个间断点ρk，在ρk处gi存在左右极限gi（）与gi（），且

（H2）存在非负常数k1,k2使得

对系统（1.1），由于其激励函数是间断的，有必要在这里对间断右端的方程的解做出解释．

定义如下：

定义2.1方程x∶［0,b）→Rn，b∈［0,+∞）是系统（1.1）在［0,b）上的解，如果：

（1）x在［0,b）上绝对连续；

（2）存在一个可测函数γ=（γ1,γ2,…,γn）T∶［0,b）→Rn，使得t∈［0,b）时，几乎处处（a.e.）有γ（t）∈K［g（x（t）］），且

对任何满足（2）的方程叫做与解x相关的输出解．由于解满足微分包含

因此，在此定义下，可以说解x为系统（1.1）的Fi l l i pov解．

定义2.2定义在［0,+∞）上，具有初值x（0）=x0的系统（1.1）解称作以ω为周期的周期解，如果x（t+ω）= x（t），t＞0．

若V∶Rn→R，且满足（i）在Rn内相关；（i i）x≠0时V（x）＞0，仅当x=0时V（0）=0；（i i i）V（x）径向无界，即‖x‖→+∞时V（x）→+∞时；则说是C相关的．

引理2.2如果V（x）∶Rn→R是C-相关的，x（t）∶［0,+∞）→Rn在［0,+∞）的任何紧集中绝对连续，则x（t）与V（x（t））∶［0,+∞）→R在t∈［0,+∞）→R上几乎处处可导，且

2 解的存在性

这一部分，主要研究了系统（1.1）解的存在与周期解的存在性．先证明了系统（1.1）在上至少存在一个解，只有在此基础上，才能对周期解的存在性与稳定性进行进一步的讨论．首先来看解的存在性．

定理2.1如果假设（H 1）与（H 2）成立，则对任意初值x（0）=x0，系统（1.1）在［0,+∞）上至少存在一个解．

证由于x（t）→Dx（t）+AK［ g（x］）+I（t）为丄半连续的集值映射，且值域非空紧凸，局部解的存在性能够得到保证．I（t）为以ω为周期，且在［0,+∞）上连续，从而I（t）有界，即存在M＞0，使得‖I（t）‖≤M．对t∈［0,+∞）几乎处处有

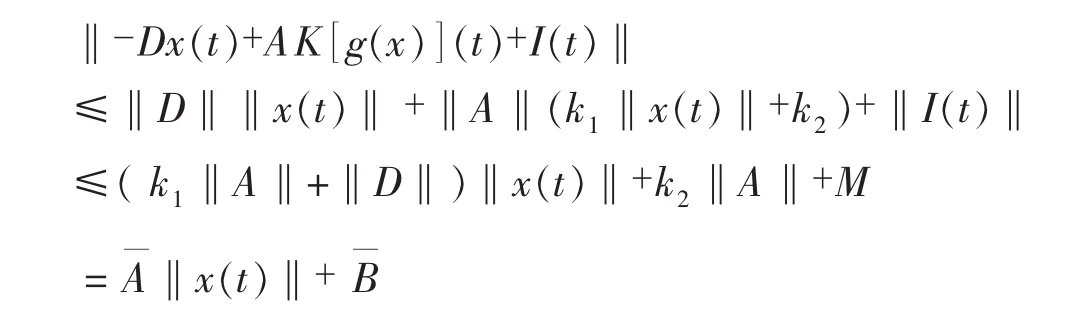
根据Gronwal l-Bellman不等式可以得到

由延拓定理，此定理得以证明．

3 结论

这篇论文，证明了Hopfield神经网络解的存在性，其中网络的激励函数可以是无界或非单调的.这比先前以激励函数为单调或有界为前提的研究有所突破．

［1］J.P.A ubin,A .C elliana.differentialInclusions［M ］.B erlin：Spring-V erlag,1984.

［2］J.P.A ubin,H .Frankow ska.Set-valued A nalysis［M ］.B oston：B irkauser,1990.

［3］J.P.A ubin.Viability Theory［M ］.Boston：B irkauser,1991.

［4］F.H .C larke.O ptim ization and nonsm ooth A nalysis［M ］.N ew Y ork：W iley,1983.

［5］Q . D ong, K . Matsui, X . Huang. Existence and stability of periodic solutions for H opfield neural netw orks equations with periodic input［J］.N onlinearA nal.2002（49）：417～479.

［6］J.D ugundji,A .G ranas,Fixed PointTheory,in:M onografie M atem atyczne,vol.123,PW N ,1982.

［7］A .F. Filipov.D ifferential E quations W ith D iscontinuous R ight-H and Side ［M ］. B oston：M athem atic and its A pplications（SovietSeries）,K luw erA cadem ic,1988.

［8］M . Forti, P. Nistri. Global convergence of neural netw orks with discontinuous neuron activations, IE E E Trans ［J］. C ircuits Syst.2003，50（11）：1421～1435.

（编辑 郭继荣）

O175.1

A

1673-1808（2014）03-0020-02

2014-03-22

潘玉峰（1979-），男，山西静乐人，晋中学院数学学院，讲师，硕士，研究方向：非线性分析.