一种基于混沌理论的数字图像置乱新算法

何 冰

(渭南师范学院物理与电气工程学院,陕西渭南 714099)

一种基于混沌理论的数字图像置乱新算法

何 冰

(渭南师范学院物理与电气工程学院,陕西渭南 714099)

提出一种基于混沌理论的数字图像置乱新算法.首先将混沌序列按照从小到大的顺序进行排列,然后对排序后的每个元素对应的编号以集合序列的形式记录下来,形成密钥流.最后按密钥流形成的索引值对相应位置上的像素进行位置置乱,并将位置置乱后的两相邻的像素值进行异或运算得到最后的加密图像.实验结果表明:该算法具有良好的置乱效果,使置乱后的图像相邻像素的相关性更小,提高了抗非法攻击的能力,增加了图像的安全性.

混沌理论;混沌序列;安全性

0 引言

数字图像置乱是指信源端借助数学或其他领域的技术,对一幅有意义的数字图像做数学变换使之变成一幅错乱无序的图像后再进行传输;在传输的过程中,即使非法截获者获得了图像也无法从错乱无序的图像中得到原始图像信息.而在信宿端,可以利用解密密钥恢复原始图像.目前数字图像置乱算法主要有:曲线变换、猫脸变换[1]、希尔伯特曲线[2]、格雷码变换[3]、混沌序列加密等.而现有的加密算法在一定程度上都存在一定的局限性.在参考文献[1]中作者将灰度图像在空间域上进行置乱操作,获得了良好的实验效果,但此算法因图像在信宿端的还原操作需要依靠后续的无损处理结果,使得该算法对于图像的压缩以及信息隐藏都有自身不利的一面.参考文献[4]中置乱涉及海量的密钥计算,同时该算法的时间复杂度较高,经过多次迭代运算后才能达到较优的置乱结果.此外,以上这些加密算法都是对灰度图像中像素点的位置进行了重新排列,但该图像本身的像素值并未发生改变,因此经过置乱的灰度图像的直方图也就保持了原始灰度图像直方图的特性.为了增强灰度图像在置乱后的隐秘性和安全性,提出了一种利用混沌序列置乱新算法.首先对混沌序列按照从小到大的顺序进行排列,然后将排序时每个元素对应的编号以集合序列的形式记录下来,形成密钥流.最后按密钥流形成的索引值对相应位置上的像素进行位置置乱,并将位置置乱后的两相邻像素值进行异或运算得到最后的加密图像.本文设计的新算法使得灰度图像的直方图在经过处理之后分布特征更像高斯白噪声,这样增强了图像在网络传输过程中的安全性能.

1 混沌学理论的图像置乱

Logistic映射从数学角度来看是一个非常简单的混沌映射,其数学表达公式如下:

约束条件为:0＜u≤4,xn∈[0,1].

其中:u称为Logistic控制系数.当u确定后,由任意初值x0∈[0,1],可迭代出一个确定的序列x0,x1, x2,…,xn,对于不同的u值,式(1)将呈现不同的特性,随着参数u的变化,混沌系统将不断地经历倍周期分叉,最终达到混沌.当u→4时,系统稳定点的周期达到无限长时进入混沌状态.

2 新算法设计步骤

2.1 新算法正变换

令原始灰度图像I的大小为M×N(实验中图像为Lena图像,大小为256×256).

Step1:将原始灰度Lena图像I进行Z字形扫描(如图1)形成一维向量R(i),i∈(1,2,3,…,M×N).这样一方面起到降维作用,另一方面二维数据变换成一维数据后便于后续置乱算法操作.

Step2:选取合适的参数μ和初值x0作为Logistic映射的密钥,根据原始图像的大小生成一维混沌序列L,L={x1,x2,x3,…,xM×N}.

Step3:对一维混沌序列L按照从小到大的顺序排列,同时记录其排列的索引值得到索引集合T.

Step4:将一维向量R(i)按照索引集合的顺序重新排列生成新的一维向量.

Step7:依次将每个元素与V(i-1)相异或,得到S(i).按照换位规则将之进行交叉换位得到V(i). V(i)即为置乱后的一维向量,根据实际需要可以将V(i)自适应的恢复成大小为m×n的图像.

2.2 新算法逆变换

新算法逆变换是图像置乱算法的逆过程,具体步骤如下:

Step1:首先将V(i)进行自换位操作,换位操作与图2相同.即第1位与第8位互换,第2位与第7位互换,第5位与第6位互换,第4位与第3位互换,换位后得到S(i),然后将S(i)与V(i-1)相异或,得到R′(i).

Step2:依次对V(i-1)做同样的操作,即先对其交叉换位,然后与其前一元素的灰度值相异或得到R′(i-1).

Step3:最后对V(1)进行自换位,得到S(1),然后将其与255相异或得到R′(1).

Step4:依据解密密钥,即使用参数μ和初值x0,根据Logistic映射数学表达公式生成一维混沌序列L,L ={x1,x2,x3,…,xM×N}.

Step5:对一维混沌序列L按照从小到大的顺序排列,同时记录其排列的索引值得到索引集合T.

Step6:将一维向量R′(i)按照索引集合的顺序重新归位生成新的一维向量R(i).

Step7:将生成的R(i)(i∈{1,2,3,…,M×N})进行Z字形扫描归位得到大小为m×n的恢复图像.

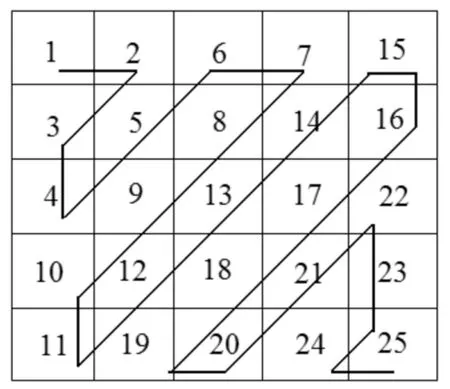
图1 Z字形扫描过程

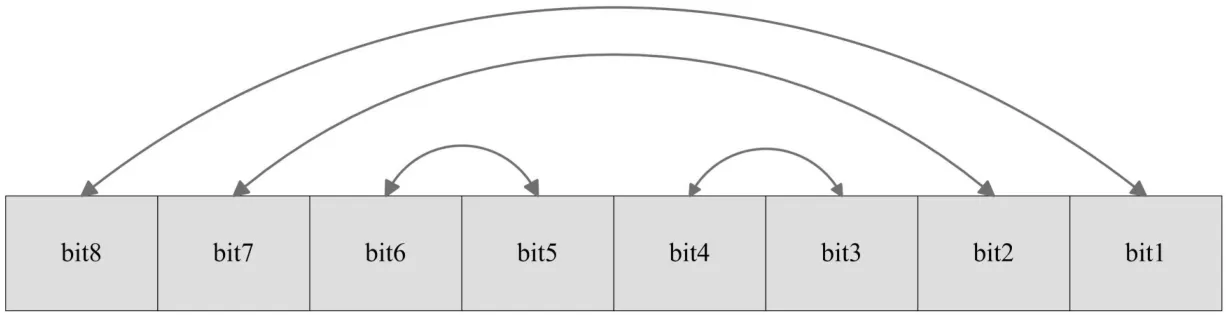
图2 序列交叉换位示意图

3 Matlab实验结果分析

新算法实验结果主要分为两个实验进行:图3给出原始图像和原始图像对应的直方图(实验1).图4给出了新算法及新算法对应的直方图与仿射变换算法的结果(实验2).

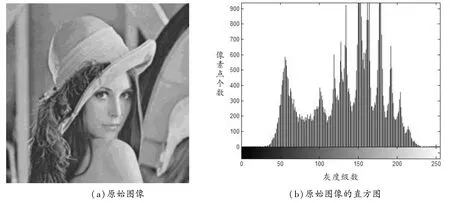
图3 原始图像及其直方图

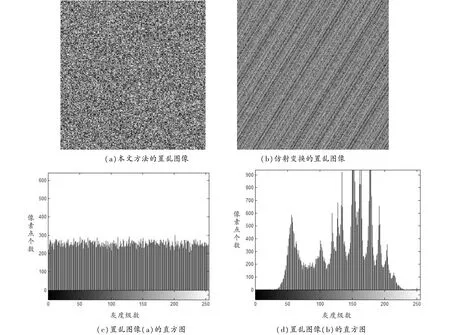
图4 置乱图像及其直方图结果对比

图4显示,与仿射变换置乱方法相比,本文置乱新算法使得图像的纹理更加均匀、像素级分布更接近高斯白噪声,从人眼的视觉系统看不出涉及到宿主图像的关键信息特征,因此此算法是最优的.而在另外一个角度,仿射变换算法与宿主图像的直方图完全相同,恶意攻击者可借此获得宿主图像的直方图等重要信息,这也是所有基于位置变换方法的一个共有的缺点.而本文新算法的直方图与原图像的直方图相比,发生了明显的变化,而且更接近白噪声.

设两幅图像灰度直方图分别为h1(k),h2(k),k=0,1,…,G-1,则定义直方图的相似度为:

对于一幅无任何杂质的纯噪声图像,其直方图分布应该是均匀的,即h1(i)=h2(j),i,j=0,1,…, G-1.根据式(2),比较仿真变换置乱和本文置乱新算法与白噪声图像灰度直方图的相似度,如表1.

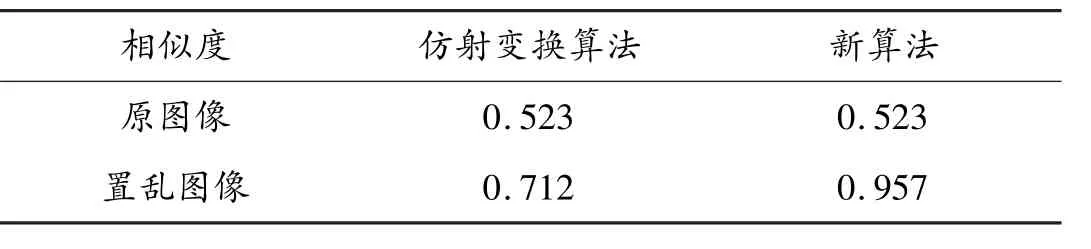
表1 仿射变换算法、新算法的高斯噪声直方图相似度

4 结语

本文提出了一种基于混沌数学理论的图像置乱新算法.实验结果证明,算法实现过程简单,适合图像在网络传输中的隐藏操作,具有较好的实用价值和应用前景.

[1]丁玮,闫伟齐,齐东旭.基于Arnold变换的数字图像置乱技术[J].计算机辅助设计与图形学学报,2001,13(4):338-341.

[2]林雪辉,蔡利栋.基于Hilbert曲线的数字图像置乱方法研究[J].中国体视学与图像分析,2004,9(4):224-227.

[3]王广超,罗来鹏.一种广义Gray及其在数字图像置乱中的应用[J].华东交通大学学报,2012,5(3):23-26.

[4]柏森,曹长修,曹龙汉.基于骑士巡游变换的数字图象细节隐藏技术[J].中国图象图形学报,2001,6(11):1096-1100.

[5]张爱华,江中勤.基于Logistic映射的混沌图像加密算法的改进[J].南京邮电大学学报,2009,29(4):5-9.

[6]丁玮,齐东旭.数字图像变换及信息隐藏与伪装技术[J].计算机学报,1998,21(9):839-843.

[7]何冰.基于仿射变换的图像置乱改进新算法[J].计算机与数字工程,2011,(3):122-124.

[8]袁玲,康宝生.基于Logistic混沌序列和位交换的图像置乱算法[J].计算机应用,2009,10(2):8-10.

【责任编辑 牛怀岗】

A New Digital Image Scrambling Algorithm Basic on Chaos Theory

HE Bing
(School of Physics and Electronic Engineering,Weinan Normal University,Weinan 714099,China)

By using the Logistic mapping sequence of non-periodic,random,non-repetitive,not convergence but bounded these special properties,an improved digital image scrambling encryption algorithm based on chaos theory is proposed.Firstly the order of Logistic chaotic sequence is ranked from small to large,then the code that corresponds to each element is recorded by group sequence,which called key stream.Finally the corresponding pixel position is scrambled by index value which is formed by key stream.Meanwhile,the encrypted image is formed by XOR operation of two pixel values.The simulation results show that the proposed method has good scrambling effect,which makes the correlation of neighboring pixels of encrypted image become smaller,enhances the ability of the anti-illegal attacks and improves the security of the image.

chaos theory;chaotic sequence;image security

TP309

A

1009-5128(2014)07-0016-04

2014-01-07

陕西省军民融合研究基金项目:水印技术在中小企业版权保护中的应用(13JMR16)

何冰(1982—),男,陕西合阳人,渭南师范学院物理与电气工程学院讲师,工学硕士,主要从事图像处理、信息隐藏、数字水印研究.