利用动态规划模型优化天然气产销调度问题

张宁丽 马燕 张相芬 徐晓钟

(上海师范大学信息与机电工程学院,上海 200234)

利用动态规划模型优化天然气产销调度问题

张宁丽 马燕 张相芬 徐晓钟

(上海师范大学信息与机电工程学院,上海 200234)

在不确定条件下,如何优化天然气产销调度使得产销平衡,是天然气公司急待解决的问题。天然气的购买和销售是一个多阶段动态过程,所以将动态规划理论应用其中,建立以天然气公司最大收益为目标的动态规划模型,并进行时间复杂度分析。结果表明,动态规划算法能从时间与空间角度实现天然气的合理调度;与线性求解过程相比,动态规划算法对具有最优解的实际问题的求解更加灵活,且计算量小,结果更可靠,为天然气产销优化调度提供了新的解决方法。

天然气 产销平衡 动态规划 最大收益 线性规划 时间复杂度

0 引言

在天然气产业中,天然气公司的主要任务是购买和销售天然气。但是由于其购进和销售的价格各不相同,如何在综合考虑天然气的购气成本、售气收入以及其他的基础设备损耗等一些不确定因素的条件下,实现天然气的有效购买与分配,达到天然气公司的最大收益,是目前天然气产业急待解决的问题[1]。天然气的生产与销售是一个连续的过程,同时上游油气企业为保证气田的供气稳定性,一般依据“照付不议”合同对天然气公司供气,以保证天然气的供销平衡[2]。在这种情况下,可以建立线性规划模型[3],利用单纯形法求解。但由于其产地与销售地点相距较远,市场的需求具有波动性,所以存在时间与空间上的不均匀性。

为了实现天然气的合理调度,本文将动态规划理论应用于天然气产销优化配置的研究中,建立动态规划模型,求出天然气的最优配置,为天然气的进一步研究提供参考。

1 动态规划模型的建立及求解思路

1.1 基本假设

①假设天然气公司从各个气源的购气费用与购气量呈正比例关系,其向各用户销售天然气所获得的售气收入与售气量也呈正比例关系,即:

式中:ci为天然气公司从气源i购进单位天然气的价格;Q1i为一段时期内,天然气公司从气源i购进的天然气量;Ci为一段时期内,天然气公司从气源i购进Q1i天然气的总费用;sj为天然气公司向用户j销售单位天然气的价格;Q2j为一段时期内,天然气公司向用户j销售的天然气的总量;Sj为一段时期内,天然气公司向用户j销售Q2j天然气的总收入。

②假定向第j个用户销售一定量的天然气时,天然气管道的运行费用和压气站的运行费用考虑为一个常数Cj。

③在目标函数中不考虑管道、压气站的人工和设备维修费用,因为这些费用通常与管网的运行方案无关,对天然气公司的销售收益不会有影响[4]。模型中没有考虑天然气的储气部分,所以假设天然气的产销是平衡的。

1.2 建立动态规划模型

天然气产销运行包括天然气的生产、购买和销售,所以在建立的动态规划模型中应包括气源、天然气公司和用户三个参与者[5]。在一定时间段内,可以从N个气源购进天然气,根据“照付不议”合同,在产销平衡的基础上,将所购进的天然气全部销售给M个用户,其中包括M1个可中断用户和M2个不可中断用户(M1+M2=M)。气源、天然气公司和用户之间的供求关系如图1所示。

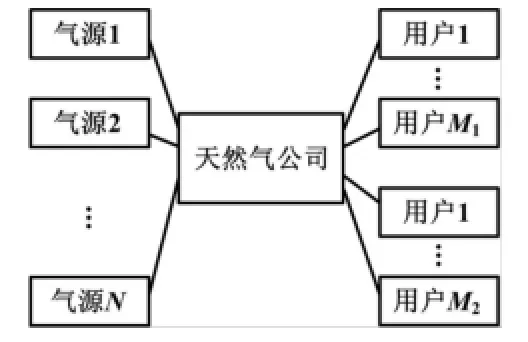
图1 气源、天然气公司和用户三者关系图Fig.1 Relationships among gas sources,gas company and users

一般情况下,天然气产销运行的周期为一年,在供气周期的每一个调度时段,天然气公司需要在空间上对市场内不同的用户进行最优分配,以达到销售利益的最大化[6]。为使模型简单可行,同时也为保证模型的独立性,避免季节变化等因素的干扰,本文将天然气产销运行的周期进一步细化为一个月。在每个月内,以天然气公司在该阶段现有的天然气总量Qj作为状态变量,以用户个数划分阶段,具体如下[7]。

①阶段变量j。本文根据用户个数划分阶段,在该时段中有多少天然气用户,就将产销运行过程划分为多少个阶段,则有j=1,2,…,M。

②状态变量Qj。以该阶段内天然气公司现有的总的天然气量作为状态变量,假设在运行初期,天然气公司从各个气源购买的天然气总量为Q,并假定Q1=Q。

③决策变量Q2j。以天然气公司向各个用户销售的天然气总量作为决策变量,则:

式中:Q2j为第j个阶段,天然气公司向用户j销售的总的天然气量;Q2ij为第j个阶段,天然气公司向各个用户j销售的属于气源i的天然气量。

④状态转移方程:Qj+1=Qj-Q2j,即第(j+1)阶段天然气公司拥有的天然气总量Qj+1等于第j个阶段初期天然气公司拥有的天然气总量Qj与第j个阶段公司向第j个用户销售的天然气总量Q2j之差,则有QM+1=0,具体转移过程如图2所示,其中ri(Q2j)为效益函数。

图2 各阶段天然气分配量以及效益函数图Fig.2 Distribution amount of natural gas and benefit function at each stage

⑤效益函数ri(Q2j)。效益函数ri(Q2j)表示在第j个阶段,天然气公司向用户j销售Q2j的天然气时获得的收益。

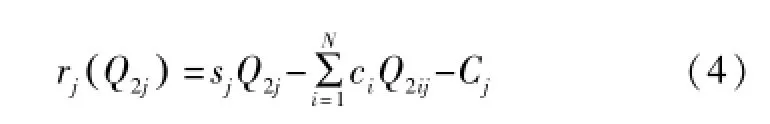
则最终目标函数为:

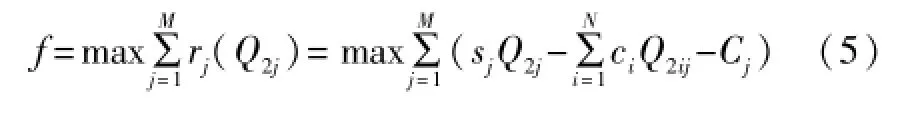
1.3 约束条件

由于每个气田和用户具有一定的供气和购气限制,所以天然气公司在天然气的购买与销售过程中应该满足以下约束条件[8]。

①在一段时期内,天然气公司向M个用户销售的属于气源i的天然气总量应该满足:

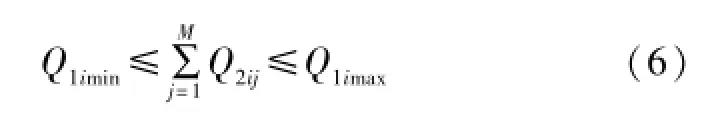
②在第j个阶段,天然气公司向用户j销售的天然气量应该满足用户的用气要求,即:

③各个时间段内,在产销平衡的条件下,M个用户的总用气量应与从N个气源购买的天然气量相等,即:

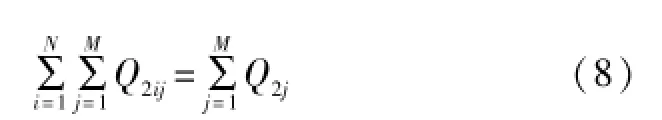
④在一段时间内,用户j总购气总量应与从N个购买的天然气的总和相等,即:

⑤各个变量的非负性约束:

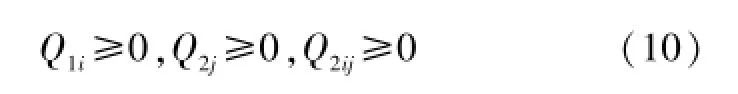
1.4 模型的求解

根据动态规划最优原理,可得基本方程[9]:

状态转移方程为:Qj+1=Qj-Q2j,逆向递推可以求得最优决策序列(Q21,Q22,…,Q2M)和公司最大收益f1(Q1)。

天然气动态规划模型的逆序算法步骤如下。

①设定初始值,取j=M+1,fM+1(QM+1)=0,Q1=Q;

②逆向递推,综合以上约束条件,依次取j=M, M-1,…,1。

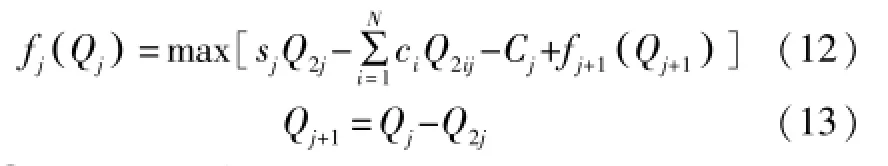
③根据初始条件fM+1(QM+1)=0,先求出第M个阶段的最优决策和最大收益,然后代入式(12),求出第(M-1)个阶段的最优决策。依次类推,求出每个阶段的最优决策和最大收益,直至求得f1(Q1),便可得到整段时期的最大收益。

1.5 算法的复杂度分析

动态规划时间复杂度=状态总数×每个状态转移的状态数×每次状态转移的时间

对应于文中所建立的产销平衡的天然气动态规划模型,根据用户个数,将模型划分为M个阶段,所以状态总数为M。每进行一次状态转移,确定一个用户的应购入量,所以每个状态转移的状态数为1。每次状态转移需要确定该用户从天然气公司购买的属于各个气源的天然气量,模型中共有N个气源,因此,每次状态转移需要的时间为N,因此该算法的时间复杂度为O(MN)。

根据所得到的目标函数和约束条件可知,该模型也是一个线性规划模型,可以利用单纯形法来求解。因此,对比于线性规划,本文采用的动态规划法真正起到了去除"冗余"和降维的作用[10]。

2 实例计算及结果分析

以图3所示的输气管网为例,这是一个包含两个气源(A,B)、两个用户(D,E)和天然气公司C的输气管网。下面制定计划期为一个月的管网最优输配气方案。

图3 天然气输送管网示意图Fig.3 Schematic diagram of natural gas transportation pipeline network

已知条件:从气源i购买天然气价格ci,气源i可以提供的天然气最小量为Q1imin,最大量为Q1imax,气源数据如表1所示。

表1 气源数据Tab.1 Data of gas sources

天然气公司向用户j出售天然气价格sj、用户j可以购买的天然气最小量Q2jmin、最大量Q1imax,每个用户购买天然气时压气站和管道所产生的固定损耗Cj,用户数据如表2所示。

表2 用户数据Tab.2 Data of users

根据用户个数,将求解过程划分为两个阶段,由此可得动态规划基本方程为:

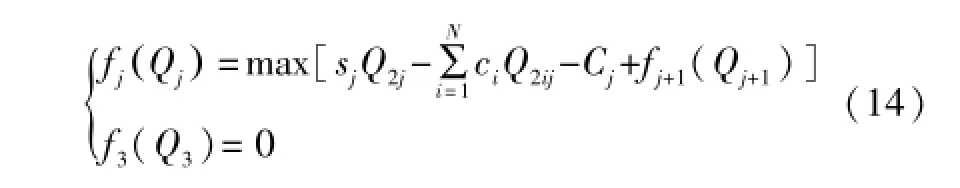
约束条件为:

第一阶段:

第二阶段:

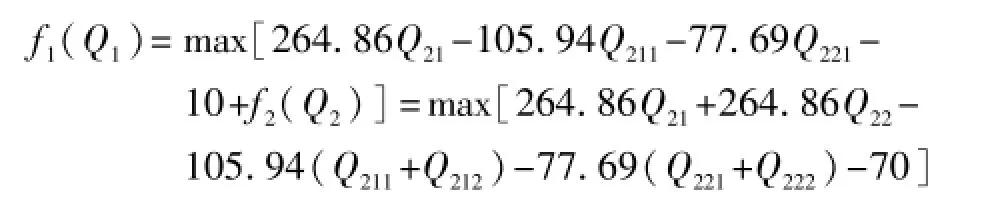
根据已知的约束条件,可得各个阶段的最大收益和最优决策:f1(Q1)=13 212.93、Q21=14.781、Q211=14.781 [Q221=0、f2(Q2)=12 853.93、Q21=71.217、Q211=14.717、Q221=56.5。

对比两种求解过程,本文所用动态规划求解算法更具灵活性,其充分考虑了变量在计算过程中不确定的因素,且计算量更小、结果与实际状况更吻合。

结果分析如下。

①由于气源B的气价低于A的气价,在满足约束条件的前提下,应尽量购买气源B的天然气,这与实际情况相符。

②对比于单纯形法,利用动态规划求解时,不但能够得到全局的最优配置,而且可以得到每个阶段的最优配置。由最终结果可知:用户D是一个可中断用户,若实际需求有变化,可以适当地调整用户D和用户E的天然气分配量,使模型更具灵活性。

3 结束语

本文针对天然气管网不稳定运行的特点,将动态规划运用于天然气产销运行优化调度的研究中。试验证明,动态规划法为我们去解决“在哪些条件下才能达到整体最优”的问题提供了有效的途径,尤其对于求解有上下限约束条件问题特别有效。为了简化模型,文中未考虑压气站和储气库部分。模型中所选的运行周期为一个月,这样可以使模型具有一定的独立性,不必考虑季节变化对其造成的影响。现实中的天然气管网模型是非常复杂的,要受到各种因素的制约,在此本文仅考虑相对简化情形,为相关的计算提供一个参考的平台。

[1] 彭赟,成金华,王小林,等.基于多目标动态规划的天然气产销运行优化调度[J].经济纵横论,2012(8):128-131,184.

[2] 周章程,陈国群.天然气长输管道管输价格模型[J].油气储运, 2004,23(11):44-46.

[3] 裘哲勇.燃气输配的数学模型[J].数学的实践与认识,2004, 34(12):1-7.

[4] 蒋维,陈开,钟晓,等.基于动态规划的资源受限随机工序调度[J].计算机工程,2008,34(16):19-21.

[5] 李波.天然气管网系统输配气运行方案优化[J].石油规划设计,2001,12(6):22-25.

[6] Bopp A E.An optimization model for planning natural gas purchases, transportation,storage and deliverability[C]∥Omega,International Journal of Management Science,1996,24(5):511-522.

[7] Hamedi M,Farahani R Z,Husseini M M.A distribution planning model for natural gas supply chain:a case study[J].Energy Policy,2009(37): 799-812.

[8] 唐德善,周之豪,许连成.动态规划法在复杂水资源系统分析中的应用[J].运筹与管理,1993(3):48-53.

[9] 孙素云.基于动态规划的多链路出口路径选择算法[J].计算机工程,2010,36(9):117-119.

[10] 李书波,仙立东.运筹学在燃气输配系统中的应用[J].系统工程理论与实践,1997(6):135-138.

Optimizing the Production and Marketing Dispatching of Nature Gas by using Dynamic Programming Model

How to optimize the production and marketing dispatching of natural gas and make the balance of production and sales under uncertainty is a pressing problem for the natural gas company.As the purchase and sales of natural gas is a dynamic process with multiple stages,so the dynamic programming theory is applied to solve this problem.The dynamic programming model with target of maximum benefit of the natural gas company is established,and the analysis of time complexity is conducted.The result shows that the reasonable dispatching of natural gas can be implemented from both time and space angles by this dynamic programming algorithm.Comparing with linear programming algorithm,the algorithm proposed is more flexible,more reliable,and with less calculation amount for solving practical problems and getting optimal solution,it provides new approach for the optimal production and marketing dispatching of natural gas.

Natural gas Balance of production and sales Dynamic programming Maximum benefit Linear programming Time complexity

TE832

A

上海市部分地方院校能力建设基金资助项目(编号:11510502400)。

修改稿收到日期:2014-02-07。

张宁丽(1990-),女,现为上海师范大学计算机软件与理论专业在读硕士研究生;主要从事天然气的最优调度研究。