基于模糊控制的抛射机器人位置校准研究

孔德松 高宏力 张洁 赵彬 黄晓蓉 杨松

(西南交通大学机械工程学院,四川 成都 610031)

基于模糊控制的抛射机器人位置校准研究

孔德松 高宏力 张洁 赵彬 黄晓蓉 杨松

(西南交通大学机械工程学院,四川 成都 610031)

针对抛射机器人距离目标位置较远,在位置校准过程中容易出现目标位置判断不准、校准速度慢等问题,提出了定距离的位置校准方式。在选用高精度激光扫描仪提高位置判断精度的基础上,构建了精准的数学模型,同时在算法中加入了模糊控制。试验结果表明,该装置位置校准效果理想,符合机器人的抛射需求。

位置校准 抛射机器人 激光扫描仪 模糊控制 模糊算法

0 引言

机器人诞生于20世纪,发展非常迅速,现已应用到生产、生活的各个方面,能够替代人工完成精度更高、可靠性更强的任务和目标。

抛射机器人的研制在军事和民用中都具有非常重要的意义,但是由于抛射受到抛射距离和初速度以及空气阻力多个参数的影响,使其算法极其复杂[1]。鉴于此,抛射机器人大多选用的是定位置或者定距离的抛射方式,即在经过计算和现场试验后,得到在固定距离下抛射的最优初速度和抛射角,达到精确抛射的目的。但定位置的抛射方式大大限制了机器人的自由度和运动空间。当采用定距离抛射方式时,由于抛射方向需要严格对准目标位置,机器人位置的校准就成为了抛射能否成功的关键。对此,本文在位置监测中应用了激光扫描仪,可以针对当前位置进行非常有效和快捷的分析;在控制过程中,加入了模糊控制器,采用模糊控制不仅对被控制对象参数变化适应性强,同时使电机运行更加平稳,保证了控制精度的要求和实时性[2]。

1 总体设计

设计要求:抛射机器人需要在距离为5 m的位置向高度为3.5 m、直径为0.5 m的圆形抛射平台进行物体抛射,抛射平台立柱直径为0.1 m,机器人释放物体的高度为0.5 m。理想抛射目标位置为到达抛射平台的圆心。抛射方式采用弹射方式,即在抛射手臂上安装弹簧,在位置校准完成后,控制气阀进行物体释放。

在经过精密计算和多次重复性试验后,得到在距离为5 m的位置上,以10 m/s的初速度和71°抛射角抛射时,物体能够精确到达抛射点,并具有较好的接触角度,不会发生侧滑等情况。

为了能够使机器人更协调有效地进行角度和距离调整,底盘采用四个全向轮设计。相邻两个全向轮的夹角为90°,通过四个全向轮转动方向和差速的配合,可以进行顺时针和逆时针的原地旋转以及任意方向直线运动[3]。

1.1 系统工作原理

抛射机器人系统以倍福嵌入式PC(CX1030)为控制核心,由激光扫描仪(劳易测ROD4)、倍福模拟量输出模块(EL4004)和直流电机构成。

激光扫描仪通过串口与嵌入式PC进行通信,能够高速实时上传扫描数据,经过嵌入式PC的分析和运算,控制EL4004模块输出0～10 V电压,通过桥式驱动电路驱动直流电机的配合运行,达到控制机器人运动的目的。

1.2 激光扫描仪应用规划

德国劳易测ROD4激光扫描仪利用内置电机旋转能够对前方190°范围的目标进行高速扫描,扫描射线间隔为0.36°,可以实时返回前方障碍物的距离值。扫描频率可控,返回数据为ASCII码,共528组[4],扫描规则如图1所示。

图1 激光扫描仪扫描规则示意图Fig.1 Schematic diagram of the scanning rules of laser scanner

在距离调整过程中,理想条件下可以对采集到的528个数据进行分析,其中数值最小的一组即为距离抛射台的实际距离。若数据不够明显,则可使机器人进行180°原地旋转,再次检测。在距离值确定后锁定当前扫描线,运用机器人底盘的四个全向轮的差速配合,并以当前扫描线的指向为运动方向,直线前进或后退到达距离为5 m的位置处。

在角度调整的过程中,扇形的弧长计算公式如式(1)所示:

式中:l为扇形的弧长;n为扇形的中心角;R为扇形的半径。

2 模糊控制策略

模糊控制是建立在模糊推理基础上的基于模糊规则的非线性控制,它直接使用模糊语言模拟人的直觉或经验进行控制。基于模糊控制的算法对环境参数变化的适应性较强,而且具有较好的鲁棒性和良好的抗干扰能力[5]。

典型的模糊控制器由模糊化、模糊推理和解模糊三部分构成,它们都建立在知识库的基础上。

2.1 算法实现

抛射机器人位置校准所采用的是单输入、单输出的模糊控制方式,输入变量为激光扫描仪采集的角度和距离信号;输出变量为抛射机器人转动的角度、机器人前后移动距离。

2.1.1 输入量设置

①根据激光雷达的检测结果,机器人距离抛射平台s的隶属模糊子集定义为{远(F)、偏远(SF)、中(M)、偏近(SN)、近(N)},其隶属度函数图形如图2(a)所示。

②在位置移动到距离5 m时,根据激光扫描仪检测到数据的分布情况,定义角度信息的模糊子集如下: {左(L)、偏左(SL)、中(M)、偏右(SR)、右(R)},其隶属度函数图形如图2(b)所示。

图2 模糊控制的输入隶属函数Fig.2 Membership function of fuzzy control input

2.1.2 输出量设置

①距离调整。抛射机器人运用激光扫描仪测得的距离最小值,对机器人的距离情况进行分析和运算后,通过改变电压值来控制四个电机的前后移动方向和速度,达到点动的运动方式。行进距离的模糊子集定义如下:{后退(B)、稍微后退(SB)、中(M)、稍微前进(SF)、前进(F)}。隶属度函数如图3(a)所示。

②角度调整。由于抛射机器人底盘采用四轮夹角90°,可以对其转动任意角度。为了使角度调整更为可控并有效提高精度,将每次转角范围限制为[-π/18,π/18],其模糊子集定义如下:{左转(TL)、稍微左转(STL)、中(M)、稍微右转(STR)、右转(TR)}。转动角度隶属函数图如图3(b)所示。

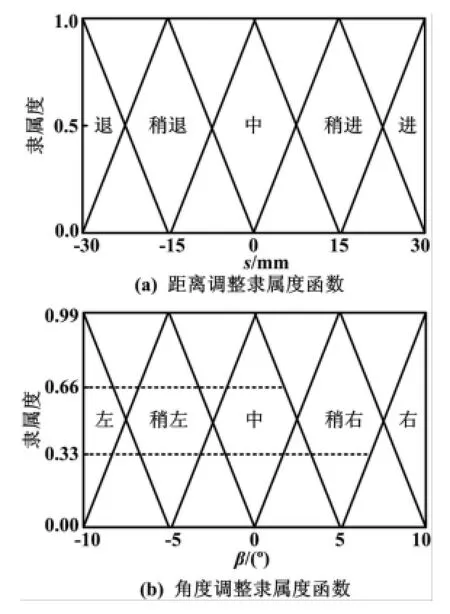
图3 模糊控制输出隶属函数Fig.3 Membership function of fuzzy control output

2.2 模糊规则的建立

模糊规则是模糊控制的关键部分,模糊算法实际上是根据模糊规则进行设计的,是采用一系列的基于专家知识的语言来描述的。专家知识常用“IF THEN”的规则进行使用,而且这些规则非常容易通过模糊逻辑条件语句进行实现[6]。举例说明:规则1,如果角度偏左,则需稍微右转;规则2,如果距离偏远,则需稍微前进。

2.3 解模糊

解模糊又称清晰化、反模糊化,是模糊控制中的关键部分,即把模糊量转换成精确量。清晰化的原因是由于模糊控制规则输出的是模糊量,而实际控制中,被控对象需要的是精确量[7]。本文采用面积重心法进行解模糊。在面积重心法中,非模糊量输出为模糊多边形面积的重心。以激光扫描仪所测得的点位为270为例,由图2(b)和图3(b)可得到如图4所示的模糊多边形。

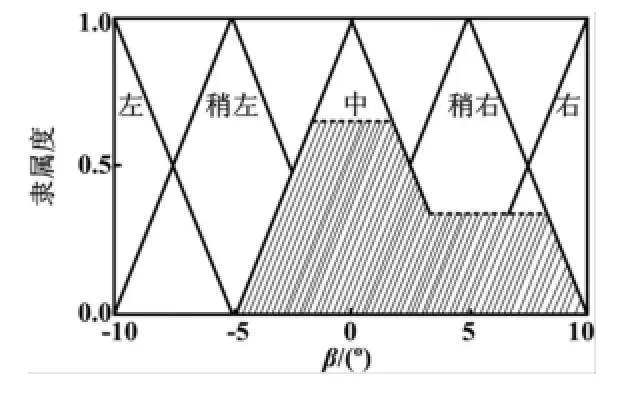
图4 面积重心法解模糊图Fig.4 Centroid defuzzification method

精确化计算公式为:

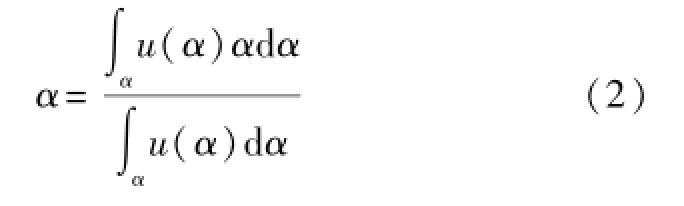
式中:α为转角的角度数;u(α)为隶属度函数。

将阴影图形分成两个三角形、一个长方形和两个梯形分别进行计算,得到α=1.81°,从而得到在扫描点为270时需要右转1.81°。扫描点数270～265所对应的5个扫描线的角度为5×0.36°=1.8°,所对应的角度相差仅为0.01°,误差较小,可以满足抛射机器人的角度调整。

模糊控制器所得出的角度调整和位置移动信号,经嵌入式PC分析后,能对直流电机进行有效的供电调节,达到定角度转动的目的。

3 系统的软件设计

抛射机器人的调节控制的软件流程图如图5所示。

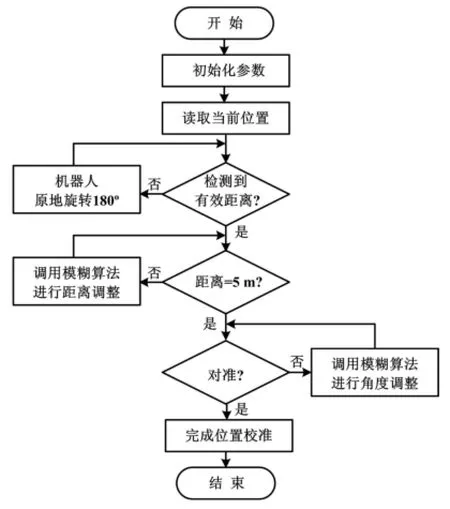
图5 控制流程图Fig.5 Control flow

首先,开机设定每个参数的初始值,将模糊控制规则存储于嵌入式PC的寄存器中,利用串口将采集到的激光扫描仪信息进行分析并判断其所对应的模糊论域;调用模糊算法求得模糊输出量,并经过尺度变换,通过模拟量输出模块EL4004输出0～10 V电压控制控制电机,实现机器人的运动。

4 现场应用情况

由于本文研究的侧重点在于抛射机器人的位置校准,故在模型实体设计时只制作了应用全向轮的机器人底盘。试验选择相对空旷的场地,并人工排除了其他障碍物的影响。

在试验过程中,对激光雷达数据进行了实时存储。

由于激光雷达的数据量非常庞大,故以500 ms为选取周期进行典型数据的选取,其他位置进行插值处理。激光雷达在位置校准过程中的数据变化曲线如图6所示。

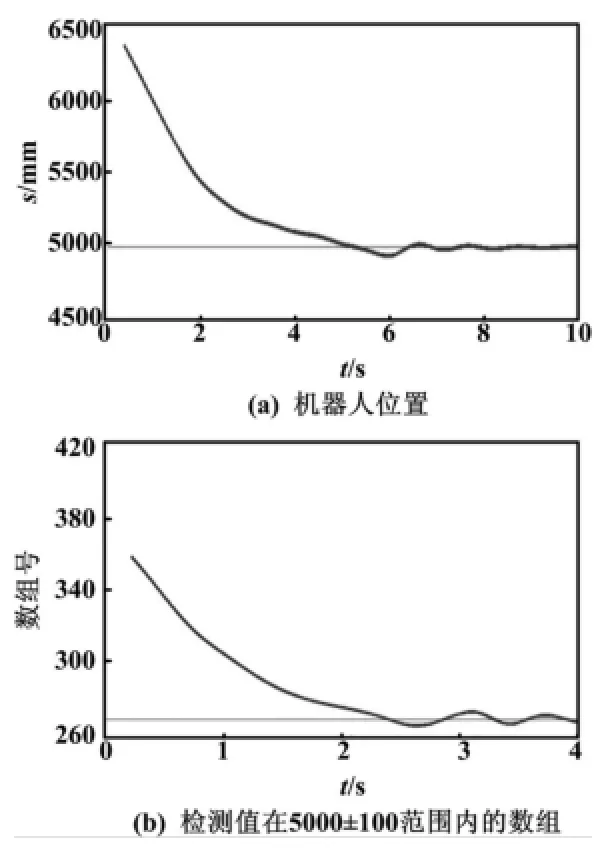
图6 激光雷达数据变化曲线Fig.6 Data changes curves of laser scanner

5 结束语

本设计以嵌入式PC为核心控制器,并以激光扫描仪作为状态调整传感器,加入了模糊控制策略。试验结果表明,机器人能够较为快速地完成位置校准操作,虽然在角度调整过程中有轻微的震荡,但是由于抛射平台的直径为0.5 m,能够允许的误差较大,故位置校准的研制能够很好地抛射机器人的位置校准要求。

[1] 李武刚.阻力系数和物体质量对斜抛运动影响的数值分析[J].广西师范学院学报:自然科学版,2006,23(2):112-114.

[2] 张永胜,高宏力,刘庆杰.基于模糊控制理论的同步带恒张力控制系统[J].机械设计与制造,2012(6):15-17.

[3] 陈旭东,孔令成,刘尊彭.基于全向轮的机器人移动机构运动分析与控制设计[J].测控技术,2012,31(1):48-56.

[4] 刘训非,张首峰.模糊控制技术在智能吸尘器自动充电中的应用[J].电气传动,2012(12):52-55.

[5] 李莲,李立.基于模糊控制的LED路灯控制系统的理论研究[J].照明工程学报,2012(8):80-83.

[6] 付宜利,顾晓宇,王树国.基于模糊控制的自主机器人路径规划策略研究[J].机器人,2004,26(6):548-552.

Research on the Position Calibration Based on Fuzzy Control for Projectile Robot

Normally,the projectile robot is located far from the position of target,in position calibration process,inaccurate judgment of the target position occurs often,and the calibration speed is slow,thus the position calibration method with given distance is proposed.By selecting high precision laser scanner to enhance the accuracy of position judgment,the accurate mathematical model is built;in addition,fuzzy control is added in the algorithm.The experimental result shows that the device offers good position calibration effect,and meets projectile demand for robots.

Position calibration Projectile robot Laser scanner Fuzzy control Fuzzy algorithm

TP249

A

国家自然科学基金资助项目(编号:51275426);

中央高校基本研究业务费专项基金资助项目(编号:SWJTU09CX019)。

修改稿收到日期:2014-02-10。

孔德松(1989-),男,现为西南交通大学测试计量技术及仪器专业在读硕士研究生;主要从事自动控制及信号处理方面的研究。