基于OCA客观聚类的RBF神经网络的研究

黄 静，张 江

（浙江理工大学信息学院，杭州310018）

基于OCA客观聚类的RBF神经网络的研究

黄 静，张 江

（浙江理工大学信息学院，杭州310018）

影响RBF神经网络性能的关键因素是基函数中心的选取，而目前尚没有可靠的方法选取RBF神经网络的中心。基于GMDH理论的OCA客观聚类具有能够自动确定最优聚类个数的优点。将OCA聚类应用于RBF神经网络中，用以自适应确定隐节点数目和各径向基函数中心，克服了传统RBF网络不能客观确定隐节点数目的缺点。实验仿真结果表明，基于OCA客观聚类的RBF神经网络具有自适应性、正确率高和训练速度快的优点。

RBF神经网络；OCA客观聚类；隐节点数目；基函数中心

0 引 言

RBF神经网络首先由Broomhead和Lowe提出。由于其具有结构简单、学习速度快、能够逼近任意非线性函数的优点，因此广泛应用于模式识别、非线性函数逼近等有实时性要求的领域［1］。已有研究表明，影响RBF网络性能的关键因素是基函数中心的选取，而一般RBF网络所利用的非线性激活函数形式对网络性能的影响并非至关重要。目前，确定RBF网络中心的方法主要有：随机选择法、自组织学习法和正交最小二乘法（OLS）等［1-2］。随机选择法选择中心，可能会出现两个中心非常接近的情况，解线性方程组时出现奇异矩阵，导致解的结果不可靠。因此，随机选择法只适用于给定样本数据具有代表性的问题。通过自组织学习进行聚类，选取聚类中心作为RBF中心，常用的方法有K-均值聚类、最近邻聚类和模糊聚类等，但都必须先给出聚类个数。正交最小二乘（OLS）方法源于线性回归模型，是一种应用较多的方法，但是不能进行迭代训练。

乌克兰科学院Ivakhnenko A G提出了基于自组织数据挖掘思想GMDH（数据分组处理方法）的OCA客观聚类［3］。OCA客观聚类能够自适应地确定聚类个数，RBF通过取各类样本的平均值作为相应隐节点的数据中心。因此，基于GMDH的RBF神经网络不需要给出聚类个数，并且能够进行迭代训练。本文通过对膨胀土分类实验的仿真，验证了基于OCA客观聚类的RBF神经网络性能。

1 RBF神经网络

RBF神经网络是一种常用的前馈网络，拥有很强的非线性拟合能力，可以映射任意复杂的非线性关系，而且学习速度快，结构简单。Poggio和Girosi已经证明，RBF网络是连续函数的最佳逼近。RBF网络采用局部激励函数，很大程度上克服了BP神经网络训练过程很长、容易陷入局部极小值的缺点［4］。RBF神经网络包括三层：输入层、隐层和输出层［5］。输入层由一些感知单元组成，它们将网络与外部环境连接起来。RBF网络仅有一个隐层，它执行从输入空间到隐藏空间之间进行非线性变换。输出层是线性的，为作用于输入层的激活信号提供响应。

如图1所示，输入层有N个节点，输入层节点个数等于样本维数。隐层有P个节点，各隐节点的基函数的形式为：

图1 RBF神经网络结构

基函数φ为非线性函数，训练数据点Xp是φ的中心。基函数以输入空间的点X与中心Xp的距离作为函数的自变量，一般选用Gauss函数：

Y=（y1，y2，…，yl）T为网络输出，采用线性激活函数。当输入训练集中地某个样本Xp时，对应的期望dp就是教师信号。将训练集样本逐一输入，从而确定网络隐层到输出层之间的P个权值。

2 OCA客观聚类

基于GMDH理论的OCA客观聚类具有能够自动确定聚类个数的优点。已有研究表明，OCA能对模糊对象给出更精确地近似或随机过程的预测给出更好的结果［6］。OCA算法首先计算样本两两之间的距离，构成偶极子。将偶极子分成包含相同样本数的两个子集A和B。同样的方式在剩余样本中，得到子集C和D，作为检测集。然后，对子集A和B进行聚类，利用一致性准则得到最优方案。如果最优方案多于一个，利用检测集C和D确定唯一的最优方案［7-10］。假设有n个样本｛x1，x2，…，xn｝，样本维数为m，OCA聚类具体步骤如下：

a）构造子集A、B、C和D。

b）对子集A和B进行聚类。

首先，按先后顺序对子集A和B中样本点进行编号，如表1所示，每对偶极子所对应的子集A和B中两个样本点编号相同，即编号都为（1，2，…，p）。把子集A和B中对应的每列称为一类，此时子集A和B中有k=p类。

表1 子集A和B样本点编号

然后，把子集A和B聚成k-1类。具体方法如下：计算子集A中任意两个编号样本之间的距离，将距离最小的两个编号归为一类（这两列将拥有两个相同的编号），假设编号1和编号2距离最小，如表2所示。

表2 编号1，2归为一类

同样的方法，将子集B聚成k-1类。将子集A和B中对应每列进行比较，相同列的数目记为Δp。使用一致性准则：ε1=（p-Δp）/p，求出ε1的值。特别指出，若类中不止一个样本点，其它类中任意一个样本点只要和该类中其中一个样本点的距离最小，便认为这两个类距离最小。重复上述步骤，把子集A和B聚成k-2类，k-3类，……，2类，计算相应的εi值。

统计k-1，k-2，…，2类中ε=0的类数目，记为count，它们成为最优聚类方案的候选方案。显然当count=1时，唯一的候选方案即为最优聚类方案。当count＞1时，就要用到检测集C和D了。

c）对子检测集C和D进行聚类。

聚类过程同步骤b）一样。考察步骤b）的几种候选方案，看哪种方案的ε在检测集C和D上最小。这个唯一的聚类方案，便是要找的最优聚类方案。

从上述过程可以看出，OCA客观聚类能够客观地确定聚类个数，得出最优方案，而不需要有先验知识。

3 基于OCA客观聚类的RBF神经网络

由于OCA聚类能够客观正确地对样本进行聚类，从而获取最佳基函数数据中心。采用OCA聚类的RBF神经网络实现步骤如下：

a）确定RBF神经网络的训练样本、测试样本、输出层节点数目。样本的维数作为输入层节点数目；

b）用OCA聚类方法对训练样本进行聚类，得出分类个数，作为隐节点数目；

c）分别计算每类的数据中心，即平均值，作为相应隐节点的基函数数据中心；

d）利用训练样本训练隐层到输出层的权值；

e）利用测试样本对网络进行测试。

进行工程建设，首先必须正确区分膨胀土的胀缩等级。膨胀土的胀缩等级分为强、中、弱。影响因素有五项：黏粒含量、粉粒含量、液限、塑限和缩性指数。BP网络可以解决该问题，然而它存在内部结构黑箱化、收敛速度慢等缺点。下面使用基于OCA客观聚类的RBF神经网络解决该问题。

采集了23个安康胀土样本［11］，其中训练样本14个（如表3所示），测试样本9个（如表4所示）。

表3 训练样本

表4 测试样本

第一步：确定样本输入层节点数目为样本维数5。输出层节点数目为1，有3个取值：‘0’‘0.5’‘1’，分别代表弱、中、强。其中0.3以下表示‘弱’，0.3～0.7表示‘中’，0.7以上表示‘强’。

第二步：对所有样本进行归一化处理。令

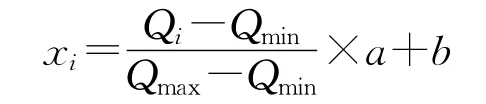
其中，Qi表示样本第i维分量，Qmin和Qmax分别表示样本第i维分量的最小值和最大值。取a=0.9，b=（1-a）/2=0.05。归一化后，保留两位小数。

第三步：对归一化后的训练样本用OCA算法进行聚类。构造偶极子如表5所示。

表5 初始偶极子

由表5可以看出，序号为6的偶极子两样本之间的距离明显大于其它偶极子之间的距离，将其舍去，使其不参与下一步的聚类。

子集A和B聚类后的准则值为：

5类时：ε=0.667；

4类时：ε=0；

3类时：ε=1；

2类时：ε=0。

检测集C和D聚类后准则值为：

5类时：ε=0.667；

4类时：ε=0.833；

3类时：ε=1；

2类时：ε=1。

在聚成4类和2类时，比较子集C和D上的准则值，取较小的准则值所对应的类数。故最优方案为：分成4类，聚类结果，如下：

第一类：1 6 7 13；

第二类：0 5 8 9；

第三类：4 11；

第四类：2 12。

故RBF的隐节点数目自动确定为4。可以看出，最优分类方案结果中没有错误的分类，即每一类都代表一个等级。计算最优聚类方案中各类的平均值，将各类的平均值作为RBF基函数的数据中心。然后利用Gauss函数计算隐层各节点输出。

第四步：使用递推最小二乘训练隐层到输出层的权值。误差限设为0.2，即当误差小于0.2时，训练结束。训练20次，平均训练次数为27，而使用BP神经网络训练，训练次数要几百甚至上千次。

使用训练好的网络对测试样本分类的结果如表6所示。

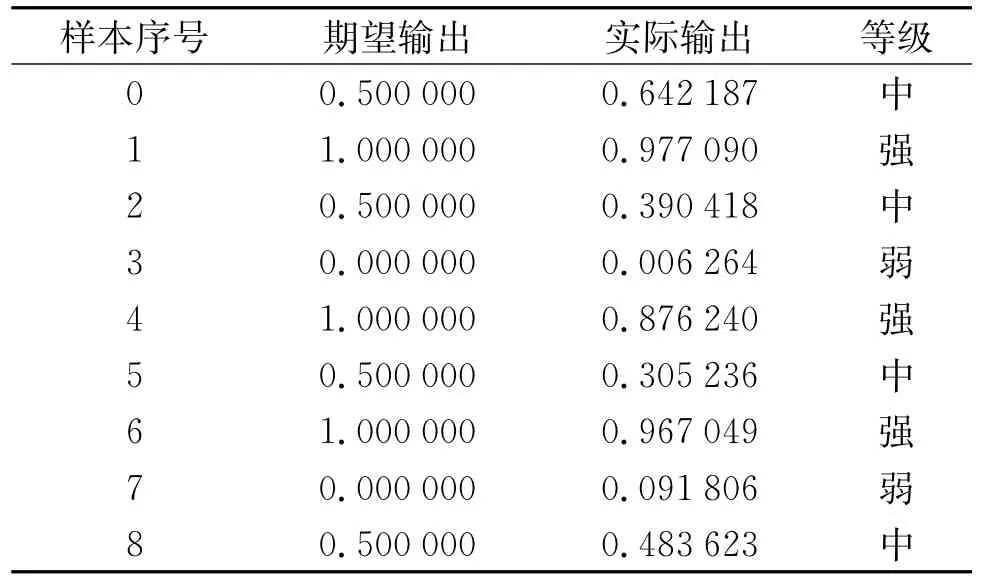
表6 测试样本分类结果

从上述可以看出，预测结果完全正确。基于OCA客观聚类的RBF神经网络不仅能够自适应客观地获取最佳基函数中心，并且训练速度快，正确率高。

4 结 论

本文针对影响RBF神经网络性能的关键因素是基函数中心的选取的研究，分析了当前基函数中心选取的各种方法的优缺点。由于OCA客观聚类具有自适应确定最优聚类个数的优点，通过分析RBF神经网络的结构，将OCA聚类应用于RBF神经网络中，用于自适应确定隐节点数目和基函数数据中心，克服了传统RBF神经网络不能客观确定隐节点中心的缺点。最后，本文通过膨胀土分类问题验证了该算法的性能，仿真结果表明了基于OCA客观聚类的RBF神经网络不仅具有自适应性，而且拥有训练速度快和正确高的优点。鉴于这些优点，基于OCA聚类的RBF神经网络在模式识别、数据挖掘和自动控制等领域必将有广阔的应用前景。

［1］施 彦，韩立群，廉小亲.神经网络设计方法与实例分析［M］.北京：北京邮电大学出版社，2009：83-85.

［2］赵清林，郭艳兵，梅 强，等.确定RBF神经网络中心点的方法综述［J］.广东自动化信息工程，2002（2）：13-15，27.

［3］Ivakhnenko A G，Mueller J A.Parametric and nonparametric selection procedures in experimental systems analysis［J］.Systems Analysis Modelling Simulation，1992，9（5）：157-175.

［4］刘 永，张立毅.BP和RBF神经网络的实现及其性能比较［J］.电子测量技术，2007，30（4）：77-80.

［5］Haykin.神经网络原理［M］.叶世伟等，译.北京：机械工业出版社，2004：256.

［6］He CZ，Xu X Z.Combination of forecasts using self-organizing algorithms［J］.Journal of Forecasting，2005，24（4）：269-278.

［7］Ivakhnenko A G，Petukhova S A，Yudin V M.Objective selection of optimal clusterization of a data sample during compensation of non-robust random interference［J］.Journal of Automation and Information Sciences，1993，26（3）：45-56.

［8］赵珩君.基于OCA的客户细分研究［J］.情报杂志，2009（1）：8-10.

［9］贺昌政.自组织数据挖掘与经济预警［M］.北京：科学出版社，2005：52-79.

［10］贺昌政，张九龙，林 嫔.基于数据分组处理方法的聚类分析模型［J］.系统工程学报，2008，23（2）：222-237.

［11］吕海波，宁世朝，赵艳林，等.SOFM神经网络在膨胀土分类中的应用［J］.土工基础，2006，20（4）：90-93.

Research on RBF Neural Network Based on OCA Objective Clustering

HUANG Jing，ZHANGJiang
（The School of Information Science and Technology，Zhejiang Sci-Tech University，Hangzhou 310018，China）

The key factor influencing RBF neural network performance is the selection of basis function center.Currently，there is no reliable method for selecting the center of RBF neural network.OCA objective clustering based on GMDH theory has the advantage of automatically determining the optimal clustering number.This research overcomes the disadvantage of traditional RBF network that it cannot objectively determine the number of hidden nodes by using OCA clustering in RBF neural network to determine the number of hidden nodes and the center of each radial basis function.The result of experimental simulation shows that RBF neural network based on OCA objective clustering has such advantages as adaptivity，high accuracy and fast training speed.

RBF neural network；OCA objective clustering；number of hidden nodes；basis function center

TP183

A

（责任编辑：陈和榜）

1673-3851（2014）01-0071-04

2013-09-12

浙江省自然科学基金资助项目（LY12F03012）

黄 静（1965-），女，杭州人，教授，博士，主要从事图像处理方面的研究。

张 江，E-mail：462098626@qq.com