透视投影下基于轨迹基的非刚体三维结构恢复研究

王 晶，包晓敏，汪亚明

（浙江理工大学信息学院，杭州310018）

透视投影下基于轨迹基的非刚体三维结构恢复研究

王 晶，包晓敏，汪亚明

（浙江理工大学信息学院，杭州310018）

基于预定义轨迹基重建的非刚体运动重建算法通常采用因式分解方法，该方法在仿射摄像机模型下恢复物体的结构信息和运动信息，未考虑深度信息，从而使算法在深度变化明显时具有较大重建误差甚至呈现病态。在基于预定义轨迹基的非刚体运动重建算法中引入一种线性迭代过程，使图像深度信息得以恢复，从而使算法在透视投影模型下可以适用。人体运动重建结果表明，提出的方法是可行和有效的。

非刚体；轨迹基；深度信息；透视投影；仿射模型

0 引 言

在计算机视觉领域中，从图像序列中恢复物体的结构信息和运动信息是一个重难点，尤其是对于非刚体物体的恢复。在过去的20年中，大量的方法被不断提出，其中，由于因式分解法具有较好的稳定性和精确性，已经被广泛应用于各个领域。

Tomasi等［1］首次提出了因式分解法，该方法运用奇异值分解（SVD）方法，在秩约束的条件下，将由图像二维特征点组成的测量矩阵直接分解为旋转矩阵和结构矩阵。他们提出的方法比较适合应用在正交投影模型下，Poelman等［2］随后将该法分别推广到透视和弱透视投影模型下。Breger等［3］将非刚体看作是刚性形状基（shape base）的线性加权组合，基于该思想，他们首次将因式分解法应用于非刚体的三维重建。Xiao等［4］引进了基约束来解决结果的歧义性。基于三维空间中特征点的时间平滑性，Akhter等［5］之后又提出了一种基于轨迹基的非刚体结构和运动恢复的算法，即将特征点的运动轨迹看作是一系列轨迹基（trajectory base）的线性加权组合。大多数的因式分解方法都是基于在仿射摄像机模型下恢复物体的结构信息和运动信息的。这种模型是对真实透视投影模型的零阶近似（弱透视）模型或一阶近似（透视）模型，该假设只有在深度变化和物体的尺寸相对于物体到摄像机的距离比较小的时候才可成立。这就意味着在恢复过程中会丢失大量的深度信息。

针对这一问题，本文在轨迹空间中，将因式分解法和线性迭代方法相结合，根据弱透视投影与透视投影之间的近似关系，通过对矩阵进行加权，运用迭代算法计算出深度信息，最终用弱透视投影模型下的结果来近似得到在真实透视投影模型下的重建结果，从而实现在透视投影模型下非刚体的结构和运动恢复。

1 仿射模型下的非刚体结构

1.1 非刚体的因式分解

在形态空间中，运动结构恢复（structure from motion）的问题可描述为：给定F帧图像序列的P个特征点｛xij｜i=1，…，F，j=1，…，P｝组成的矩阵W2F×P，恢复出物体三维结构矩阵S和旋转矩阵R。

研究通常假设非刚体模型是K个刚体形状基的近似加权线性组合，即

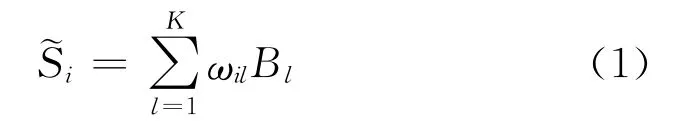
式（1）中，ωil为加权系数，Bl为形态基，K为形态基个数。当K=1，ωil=1时，则对应刚体结构的情况。

在仿射模型中，即非刚体的深度变化远小于它到摄像机的距离，对第i帧图像，有如下关系

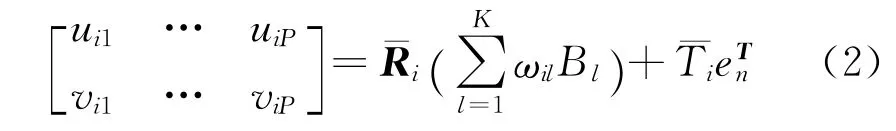
对每幅图像特征点进行坐标变换，可以使图像特征点坐标的原点位于该幅图像点集的质心，这样可以消除掉式（2）中的平移向量，则上式可以简化为

则非刚体的测量矩阵~W2F×P可以表示为

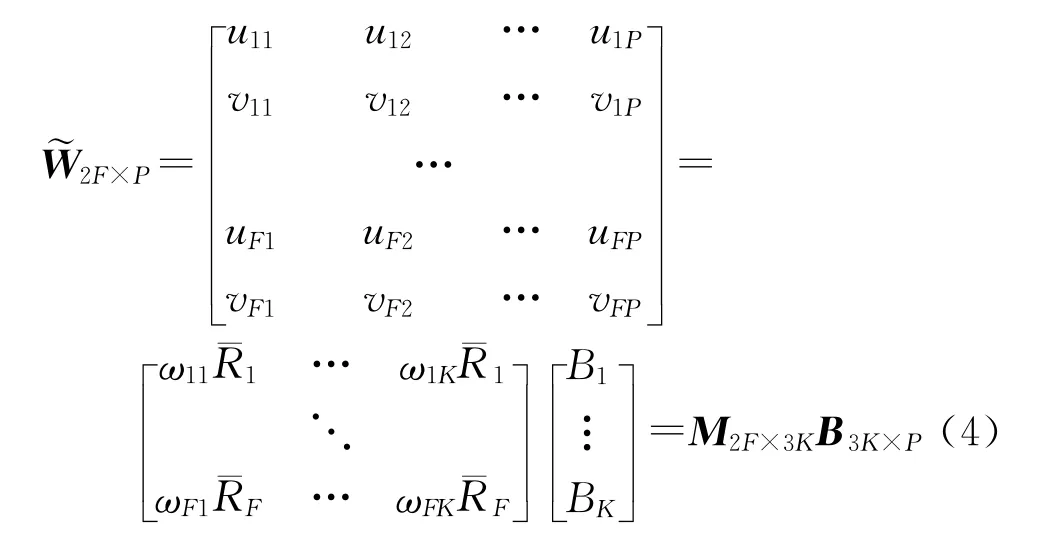
式（4）中，M2F×3K表示非刚体的运动矩阵，B3K×P表示形状矩阵。

1.2 轨迹空间中的非刚体因式分解

根据轨迹基和形态基的对偶性定理［6］，即轨迹基系数就是形态基，而轨迹基则是形态基的系数，本文采用预定义的普通离散小波变换（discrete wavelet transform，DWT）基。所以结构矩阵可以表示为一个包含轨迹基和轨迹基系数的乘积的反向投影矩阵，即

则式（4）可被分解为

为了计算校正矩阵Q，考虑矩阵Λ：

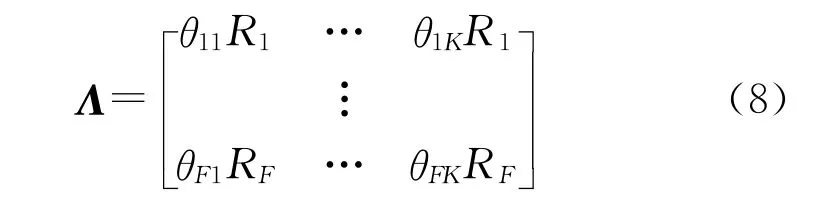
由式（8）可知，无需得到Q的整个矩阵，只需求出前三列向量即可，不妨定义Q｜｜为Q的前三列向量。结合式（7）和（8），可得

式（9）表明：当Q｜｜已知时，摄像机的投影矩阵可以计算得出，则摄像机的旋转矩阵也就可以计算出来，乘以预定义的轨迹基Θ3F×3K便可以恢复出矩阵Λ，即

为了计算Q｜｜，使用摄像机投影矩阵Ri的正交约束条件，类似于文献［1］中的方法。对于每张图像i，都满足正交约束条件［9］。

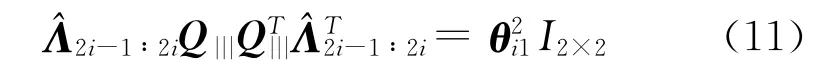
2 透视投影下的非刚体结构恢复

采用因式分解法得到的非刚体三维结构信息，大都是基于仿射摄像机模型的。且在实验过程中，采用简化摄像机模型，设所有特征点的质心均处于图像的几何中心，因此已忽略了非刚体结构的深度信息，这样会造成较大的误差。本文根据弱透视投影和透视投影之间的关系，采用线性迭代的方法，对弱透视投影模型下的恢复结果进行线性迭代，得出深度信息，来逼近真实透视投影模型下的结果。

2.1 迭代法简介

迭代是数值分析中，从一个初始估计出发寻找一系列近似解来解决问题的过程，为实现这一过程所使用的方法统称为迭代法［10］。其基本思想如下：

对于给定的线性方程组Ax=b⇔x=Mx+g，取初始向量x（0）∈Rn，构造如下单步定常线性迭代公式：

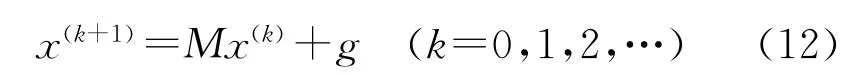
以此来产生近似向量序列x（1），x（2），…。当k充分大时，x（k）≈x*（x*为线性方程组的解）。

2.2 深度信息的获得

假设摄像机已标定，则在透视投影模型下，空间点Xi的投影点是xi，他们的关系如下：

式（13）中，mi是一非零系数，xi=［uivi1］是图像特征点的齐次坐标，R=［］T为3 ×3旋转矩阵，T=［txtytz］为3×3平移向量。

根据式（13），求得：

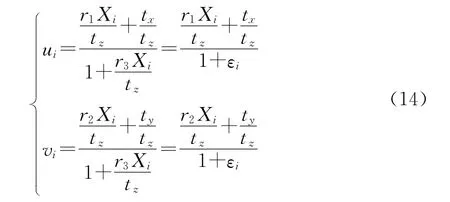
假设物体的深度和尺寸变化相对于其到摄像机的距离很小，则弱透视投影就是透视投影的零阶近似，即εi=0。令λi=1+εi，便可得到弱透视与透视投影的关系如式（15）：

图1为透视投影模型及其近似模型的比较。

根据该关系，可对式（4）进行加权，即：

首先初始化λij=1（i=1，2，…，F；j=1，2，…，P），根据式（16）和式（12）更新测量矩阵W，对测量矩阵进行线性迭代，可以求出迭代系数λij，然后重复该法直至λij收敛（即本次求得λij的值与上次求得的λij值达到误差允许的范围），最终近似恢复出透视投影模型下的结构和运动信息。

图1中，x0，xW，xP和x分别表示特征点P在正交投影、弱透视投影、平行透视投影和透视投影模型下的投影点，G表示被恢复物体的质心。

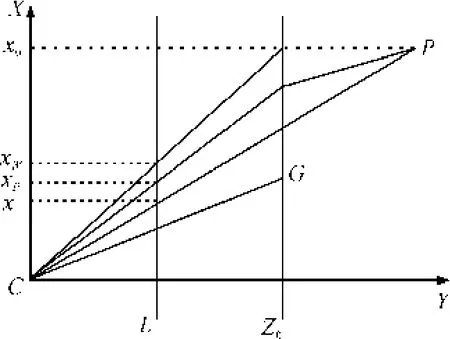
图1 透视投影模型及其近似模型比较

3 实验结果及分析

实验采用了1 102帧drink的真实图像特征点序列来对以上算法进行试验，每帧图像提取41个特征点。本实验采用简化摄像机模型，假设所有特征点的质心均处于图像的几何中心，并且摄像机的各个内置参数在整个摄影过程中均保持不变。实验中，轨迹基数目K都取为12。本文使用的数据来源于http：//cvlab.lums.edu.pk/nrsfm。

以下是任选三幅图像的实验结果。“·”是真实结构特征点，“*”是通过算法恢复出来的点。

由图2可直观地看出本文的算法较之前的算法有更好的效果，误差有了明显的改善。其中在手臂部位还有较明显的误差，存在不足，需要进一步针对这一问题展开讨论。

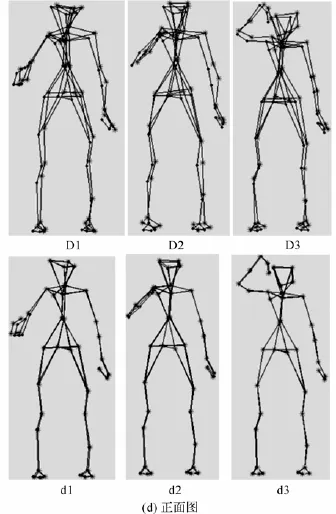
图2 3帧图像的实验结果

为了定量地分析和比较本算法的性能，根据反投影误差［10］，表1给出了先前方法和与本文方法的重建结果的误差对比结果。

反投影误差定义如下：

其中，W为原始测量矩阵，Wr为恢复结果的反投影测量矩阵。

表1 结构恢复误差分析比较

4 结 语

本文在基于轨迹基的因式分解的基础上，介绍了一种线性迭代方法。根据弱透视投影与透视投影的关系，对分解矩阵进行加权。通过迭代法计算出投影深度，从而减小误差。对真实的图像序列特征点进行实验，具有较好的结果。本文只是通过迭代法来近似透视投影模型下的结果，为确保重建算法的精确性和适用性，需进一步研究直接在透视投影模型下三维结构的恢复算法。

［1］Tomasi C，Kanade T.Shape and motion from image streams：a factorization method［J］.International Journal of Computer Vision，1992，9（2）：137-154.

［2］Poelman C，Kanade T.A paraperspective factorization method for shapeand motion recovery［J］.IEEE Trans Pattern Anal Mach Intell，1997，19（3）：206-218.

［3］Bregler C，Hertzmann A，Biermann H.Recovering non-rigid 3Dshapefrom image stream［C］//IEEE Conference on Computer Vision and Pattern Recognition，2000，2：690-696.

［4］Xiao J，Chai J，Kanade T.A closed-form solution to non-rigid shape andmotion recovery［J］.International Journal of Computer Vision，2006，67：573-587.

［5］Akher I，Sheikh Y，Khan S，et al.Nonrigid structure from motionin traiectory space［C］//Neural Information Processing Systems，2008：1534-1541.

［6］Akhter I，Sheikh Y，Khan S.Trajectory space：a dual representationfor nonrigid structure from motion［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（7）：1442-1456.

［7］孙国强.基于图像序列的非刚性物体三维结构及运动恢复［D］.长青：吉林大学，2010.

［8］Torresani L，Hertzmann A，Bregler C.Nonrigid structure from-motion：estimating shape and motion with hierarchical priors［C］//IEEE Trans.Pattern Analysis and Machine Intelligence，2008，30（5）：878-892.

［9］Akhter I，Sheikh Y，Khan S.In defense of orthonormality constraints for nonrigid structure from motion［C］//IEEE Computer Vision and Pattern Recognition（CVPR），Miami FL，June 2009：1534-1541.

［10］李庆扬，王能超，易大义.数值分析［M］.武汉：华中科技大学出版社，1986：145-150.

［11］倪晓庆.织物的三维动态仿真研究［D］.杭州：浙江理工大学，2012.

Research on Recovery of Three-dimensional Structure of Non-rigid Body Based on Trajectory Basis under Perspective Projection

WANG Jing，BAO Xiao-min，WANG Ya-ming
（The School of Information Science and Technology，Zhejiang Sci-Tech University，Hangzhou 310018，China）

To improve the stability of motion restructuring algorithm of non-rigid body，people put forward a restructuring method based on predefined trajectory basis.However，this method is still based on the affine model which does not consider depth information，thus making the algorithm have big restructuring error and even show ill condition when depth changes greatly.In allusion to this problem，this paper introduces a linear iteration process for motion restructuring algorithm of non-rigid body based on predefined trajectory basis，thus recovering image depth information and making the algorithm applicable under perspective projection model.The analysis on human motion restructuring result shows that the method put forward in this paper is feasible and effective.

non-rigid body；trajectory basis；depth information；perspective projection；affine model

TP391.4

A

（责任编辑：陈和榜）

1673-3851（2014）01-0040-05

2013-09-05

国家自然科学基金（61272311，61070063）

王 晶（1988-），女，河南辉县人，研究方向为图像处理。

包晓敏，E-mail：zjhzbxm@gmail.com