基于HHT的磨床磨削颤振特征量提取方法

陈建华，陈换过，吴 飞，张廷秀

（浙江理工大学机械与自动控制学院，杭州310018）

基于HHT的磨床磨削颤振特征量提取方法

陈建华，陈换过，吴 飞，张廷秀

（浙江理工大学机械与自动控制学院，杭州310018）

针对数控磨床磨削加工过程中的颤振现象，提出一种基于希尔伯特-黄变换的磨削颤振特征量提取方法。采用经验模式分解，将信号分解成具有不同特征时间尺度的固有模态函数分量，筛选合适的分量，提取其颤振特征量-实时方差和瞬时能量，并将其作为判断磨削发生颤振的依据。模拟仿真结果表明：基于希尔伯特-黄变换提取的磨削颤振特征量，可以作为颤振发生的判断依据。

磨削颤振；希尔伯特-黄变换；颤振特征量；瞬时能量

0 引 言

磨削加工过程中的磨削颤振是磨床主机故障的主要表现形式之一。如果在颤振孕育过程中，不能对其识别，进而采取相应的抑制措施，颤振将迅速发展加剧，会对磨削加工过程造成严重影响，因此寻求能够有效识别磨削颤振的方法就成为解决磨削加工质量的首要问题。

已有研究［1-2］表明，磨床从平稳磨削到颤振发生需要经历一段过渡磨削时期，此过渡时期的信号中包含了丰富的磨削状态信息，对于磨削颤振检测具有独特的价值。磨削颤振过渡过程的输出信号是非平稳信号，信号的频率和幅值均随时间变化，信号特征重复再现性差。针对这种磨削颤振过渡过程的特点，有必要寻求一种有效的信号特征提取和颤振检测方法。许多学者对加工过程中颤振预测都进行了研究，Bedinga等［3］采用小波包分解方法构造颤振检测特征向量，采用支持向量机对颤振进行预测；于英华等［4］以方差和互相关系数构造颤振特征量，并应用仿真进行验证；文献［5］采用小波变换的方法对颤振进行预测。文献［3-5］从不同程度上对颤振进行了预测，但都没有摆脱Fourier分析的局限，对非平稳信号的处理效果不佳。

希尔伯特-黄变换（Hilbert-Huang transform，HHT）是近年来出现的处理非线性非平稳信号的一种自适应方法［6］。该方法主要由经验模式分解（empirical mode decomposition，EMD）和希尔伯特变换（Hilbert-transform，HT）组成。EMD基于信号自身的局部特征时间为尺度，把原始信号分解为若干固有模态函数（intrinsic mode function，IMF），HT对EMD分解得到的基本分量进行相应的谱分析，可得到时频平面上的能量分布谱图，非常适合处理非线性、非平稳信号。

鉴于HHT技术在处理非平稳信号的出色表现，将其引入至磨床磨削颤振的特征提取过程，通过对磨削振动信号进行EMD分解，获得具有不同特征时间尺度的IMF，筛选合适的分量，在此基础上分析实时方差和瞬时能量随时间变化的特性，并结合颤振发生的机理，分析各分量产生的原因，提取颤振发生的征兆特征。

1 HHT基本理论

1.1 固有模态函数

IMF是学者Huang等总结瞬时频率有意义的单分量信号应满足条件的基础上提出的新概念，基于IMF的局部特性，使得函数的任何一点瞬时频率都有意义。而IMF必须符合下面两个条件［6］：a）在整个数据集上，其极值点个数和过零点的数目相等或最多相差一个；b）在任意点，由局部极大值构成的上包络线和由局部极小值构成的下包络线的均值必须为零，即信号关于时间轴局部对称。

IMF反映了信号内部固有的波动性，在它的每个周期上，仅仅包含一个波动模态，不存在多个模态重叠的现象，各IMF分量是平稳信号，具有非线性特征。

1.2 经验模式分解

EMD是将非线性、非平稳信号由高频到低频分解成有限多个IMF分量的过程，也是将信号稳定化的过程，且每个IMF包含的频率分辨率也随原始信号变化而变化，是一种自适应的多分辨率的信号处理方法。

对任意时间序列x（t），EMD可将其分解为具有不同特征时间尺度的IMF［6］，如下式所示：

其中rn（t）为振动信号趋势分量（Residual，Res），代表信号的平稳趋势，是单调函数或均值函数；c1（t）、c2（t）、c3（t）、…、ci（t）为各阶IMF分量，包含从高频段到低频段的不同信号成分。

1.3 希尔伯特-黄变换

对式（1）中的各个ci（t）作Hilbert变换得：

式中，P为柯西主值。

ci（t）和yi（t）可以合成解析函数z（t）

2 磨削振动信号特征提取方法

2.1 固有模态函数的选择

EMD分解后的IMF分量必然会存在一些伪固有模态函数。由EMD方法的正交性，可知固有模态函数是对信号的一种近似正交的表达，所以有效的固有模态函数与原始信号就会具有很好的相关性，而由于环境、噪声等产生的伪固有模态函数与原始信号的相关性较差。因此，可将固有模态函数和原始信号的相关性作为一个指标，来剔除虚假的固有模态函数，并将其作为残差的一部分。本文通过固有模态函数选择算法选择IMF：

a）对原始信号及各IMF进行归一化处理；

b）计算各个IMF和原始信号的相关系数，定义为ηi，其中i=1，...，n；

c）取固定阀值λ，对IMF进行筛选，通常λ可取最大相关系数的一个比值，即：

式（4）中，η为一个大于1.0的常数，通常取η= 10.0；

d）依次计算ηi及λ的大小（i=1，…，n），若ηi≥λ，保留第i个固有模态函数分量ci，否则将ci作为残差的一部分，即rn=rn+ci。

2.2 方差特征提取方法

磨削颤振在不同的发展阶段，信号方差是不同的，磨削颤振阶段方差明显大于平稳阶段方差。设采样信号的时间序列为｛xt｝，t=1，2，3，…，N，均值为，则方差的估值为：

然而上述公式难以用于在线分析与监视，因为只有在全部的N个采样值获得后方能计算。本文用如下的计算方法克服这一困难。

式中，R为｛Xt｝的均方值。

现在用估值计算：

写成展开的形式：

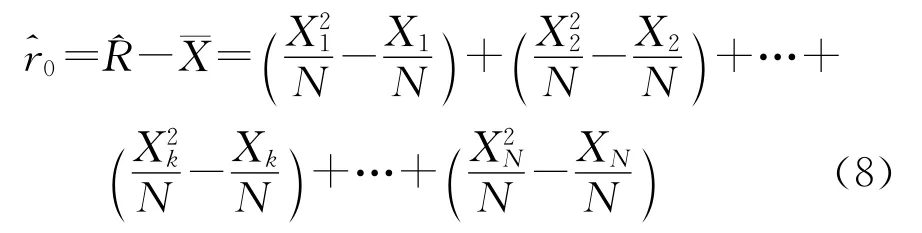
采用上式，每采样一点，则可以计算一点，但采样点数应该事先规定。可以根据式（8）实时地观察磨削振动信号的方差变化，亦可以分析已经得到的振动信号，观察振动信号的变化趋势。

2.3 瞬时能量分布特征提取方法

信号的能量可以由Hilbert变换求得［7］。根据Hilbert变换的定义，式（3）表示的振动信号的某一阶固有模态函数zi（t）的瞬时能量分布为

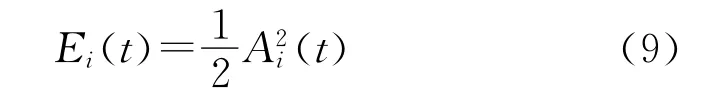
根据前面提出的固有模态函数的选择方法，筛选与原始信号有较大相关性的固有模态函数，排除贡献较小的趋势项，得到振动信号x（t）的主要频带的瞬时能量分布：

式中，E（t）表示系统在任意时刻t的主要频带瞬时能量的大小，描述了系统在不同时刻的能量转移和波动的历程，实时地反映出系统内部结构状态变化情况，同时能够反映出系统故障发生的时刻、故障状态及故障的演变规律。

3 基于HHT的磨削颤振特征量提取

为了研究磨床磨削过程中的振动现象，提取磨削过程中颤振的特征量，针对磨削过程中振动信号在时域、频域的特点，利用Matlab的Simulink模块对颤振信号进行模拟［8］。对模拟颤振信号进行EMD分解，筛选出与原始颤振信号相关性较大的IMF分量，对其进行相应的方差计算和瞬时能量计算，得到信号的发展趋势。

图1为平稳振动信号和颤振信号的时域波形及实时方差图。对此磨削颤振信号进行EMD分解，可将其分解为由高频段到低频段的11个IMF分量及趋势分量Res。由前面提及的固有模态函数筛选的方法，前三阶IMF分量与原始信号的相关性较好，因此前三阶的IMF分量为主要分析对象。

图1 稳态信号和颤振信号的实时方差图

对比图1所示的两种振动状态，可以明显看出当机床发生磨削颤振时，振动信号的幅值明显增大，对应的方差也开始大幅度增高，其中颤振信号的方差在采样时间足够长的情况下，将不会出现在末端发散的现象。由此可看出，信号的实时方差可以很好地显示磨床的颤振幅值变化。

在实际磨削过程中，由于材料的不均匀等影响，很可能造成信号局部发生突然增大的现象，如图2所示。对此局部发生突变的信号分析处理后，可见方差在磨削信号发生突变的位置也相应地发生了变化，而后又逐渐变小，可以反映出信号的发展变化趋势。

图2 局部突变信号及其方差图

所以方差能很好地反映出磨削振动信号的变化情况，但是仅以方差作为颤振的判断依据则容易引起误判。因此引入另外一种磨削颤振特征量，联合方差同时作为判断颤振的依据，就可相应地提高颤振判断的准确性。

对平稳振动信号和颤振信号进行EMD处理，筛选后应用式（9）计算其主要频带的瞬时能量，如图3所示。

图3 稳态信号及颤振信号的瞬时能量变化

对比图3所示的两种振动状态可以明显看出，当机床发生磨削颤振时，系统将出现异常的状态，导致系统的主要频带瞬时能量发生变化，可描述系统在不同时刻的能量转移和波动情况，进而实时地反应出系统故障发生的时刻及演变规律。

由上述分析可知：基于HHT的实时方差和瞬时能量变化，都可以作为判断颤振发生的一种依据，方差和瞬时能量组成的向量就可以作为后续颤振预报识别系统所需的特征向量。

4 结 论

本文针对磨削过程中的颤振的信号特征，提出了采取HHT的方法，对磨削振动信号进行分解，筛选出与原始信号相关性较大的IMF分量，对其进行相应的分析、处理，提取了反映磨床磨削颤振的特征量：实时方差和瞬时能量变化量，并应用仿真信号进行了验证，期望为后续的颤振预测、判断和抑制提供理论基础。

［1］吴 雅.机床切削系统的颤振及其控制［M］.北京：科学出版社，1993：20-41.

［2］王立刚，刘习军，贾启芬，等.机床颤振的若干研究和进展［J］.机床与液压，2004（11）：1-5.

［3］Bediaga I，Munoa J，Hernandez J，et al.An automatic spindle speed selection strategy to obtain stability in high-speed milling［J］.International Journal of Machine Tools and Manufacture，2009，49（5）：384-394.

［4］于英华，于兴强，徐平.以方差和互相关系数判别切削颤振的仿真研究［J］.设计与研究，2007（5）：25-30.

［5］Gonzalez-Brambila O，Rubio E，Hauregui J C.Chattering detection in cylindrical grinding processes using the wavelet transform［J］.International Journal of Machine Tools and Manufacture，2006，46（15）：1934-1938.

［6］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and no stationary time series analysis［J］.Proceedings of the Royal Society of London：Series A，1998，454：903-995.

［7］曹冲锋.基于EMD的机械振动分析与诊断方法研究［D］.杭州：浙江大学，2009.

［8］Yao Zhehe，Mei Deqing，Chen Zichen，et al.On-line chatter detection and identification based on wavelet and support vector machine［J］.Journal of Materials Processing Technology，2010，210（5）：713-719.

Extraction Method of Grinding Flutter Characteristic Quantity of Grinder Based on HHT

CHEN Jian-hua，CHEN Huan-guo，WU Fei，ZHANG Ting-xiu
（School of Mechanical Engineering and Automation，Zhejiang Sci-Tech University，Hangzhou 310018，China）

In order to research the flutter phenomenon in the grinding process of numerically controlled grinder，this paper puts forward an extraction method of grinding flutter characteristic quantity based on HHT，decomposes signals into intrinsic mode function components with different characteristic time scales with empirical mode decomposition，screens the appropriate component，extracts its flutter characteristic quantity-real-time variance and instantaneous energy and uses it as the basis for judging grinding flutter.The result of analog simulation shows that grinding flutter characteristic quantity extracted based on HHT can be used as basis for judging the occurrence of flutter.

grinding flutter；HHT；flutter characteristic quantity；instantaneous energy

TG580.21

A

（责任编辑：张祖尧）

1673-3851（2014）01-0016-04

2013-05-08

浙江省自然科学基金重点项目（LZ13E050003）；浙江省重点科技创新团队（2010R500OS）

陈建华（1987-），男，河南安阳人，硕士研究生，主要从事机械动力学方面的研究。