多目标0-1规划问题的蝙蝠算法
2014-05-24李枝勇马良张惠珍上海理工大学管理学院上海200093
李枝勇,马良,张惠珍(上海理工大学管理学院,上海200093)
多目标0-1规划问题的蝙蝠算法
李枝勇,马良,张惠珍
(上海理工大学管理学院,上海200093)
如何获取多目标问题更多的Pareto最优解具有十分重要的意义。在重新定义蝙蝠位置和速度更新公式的基础上,提出了一种用于求解多目标0-1规划问题的改进的蝙蝠算法。通过测试函数进行仿真实验,结果表明:与遗传算法、蚁群算法、元胞蚁群算法和粒子群算法相比,所提出的算法能够为多目标0-1规划问题找到更多的Pareto解,体现了蝙蝠算法在解决该问题上的有效性和优越性。
智能优化;组合优化;多目标0-1规划问题;蝙蝠算法
在很多实际问题中,往往难以用一个指标来衡量和判断一个方案的优劣,而是需要用多个目标。与单目标问题不同的是,多目标优化问题有着多种提法和模型。多目标0-1规划问题是一个经典的难题,已被归入所谓的NP⁃难问题,是否存在有效算法尚不可知。目前已有的精确算法都是指数级的,对于现实中的问题,特别是当问题规模较大时,根本无法使用传统的优化方法和技术来求解,而对于多目标的0-1规划来说,由于增加了目标函数的个数,使问题的求解复杂度进一步加大。本文主要讨论多目标0-1线性规划问题。
蝙蝠算法[2](bat algorithm,BA)是X.S.Yang于2010年提出的一种新型启发式算法,它模拟的是微型蝙蝠的回声定位原理。自该算法提出以来,已有学者将该算法应用于优化问题[2~5],他们的研究成果表明:在解决实际问题中,蝙蝠算法比粒子群算法、遗传算法和和声算法具有更大的潜能。
本文首先介绍了蝙蝠算法在迭代寻优过程中的核心方程,接着根据多目标0-1规划问题的特点,重新定义蝙蝠速度和位置的更新公式,提出了求解多目标0-1规划问题的蝙蝠算法,最后,对4个测试算例进行仿真实验,并将其计算结果与遗传算法、蚁群算法、元胞蚁群算法和粒子群算法的计算结果进行比较,比较结果不但验证了本文所提算法的有效性,而且体现出了在解决多目标0-1规划问题上,所提算法比上述算法具有更好的优越性。
1 基本蝙蝠算法
假设在一个d维搜索空间中,第i只蝙蝠在第t代蝙蝠的位置为速度为,脉冲频率为Fi,且当前蝙蝠种群最好的位置为x∗,则关于和的更新方程为
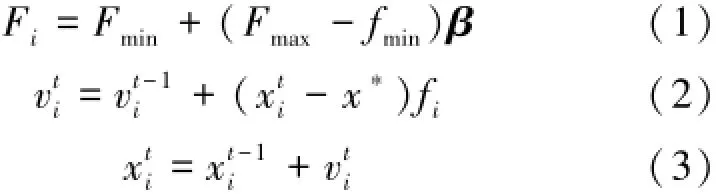
式中:β∈[0,1]是一随机向量,Fmax和Fmin分别为脉冲频率的最大值和最小值,其各个元素均服从均匀分布。
上述更新方程是针对全局搜索的,对于局部搜索,可以首先从现有的最优解集中随机选择出一个当前最好解xold,然后在其附近就近产生每只蝙蝠新待定的位置,如式(4)所示:

式中:ε∈[-1,1]是一个任意的数字,At=是所有蝙蝠在该时间步骤里的平均响度。
为保证算法在全局搜索和局部搜索之间达成一种良好的平衡关系,要求脉冲发射的响度Ai和速率ri要随着迭代过程的进行而有所更新。通常情况下,响度会逐渐降低,脉冲的发射速率会逐渐增加。具体的实现方式如式(5)和式(6)所示:

式中:α和γ是常量。对于任何0<α<1和γ>0,当t→∞时,有:→0,→。
2 求解多目标0-1规划问题的蝙蝠算法
考虑如下形式的多目标0-1规划问题:

式中:x为决策变量,Z为目标向量,记D为决策变量的可行域。
在具体求解时,采用罚函数的方法,将约束条件转化到目标函数中,将问题转化为无约束形式。
通常情况下,类似于单目标优化的最优解在多目标优化中是不存在的,只存在Pareto最优解,而且大都具有很多个Pareto最优解[1]。其含义为:记当前Pareto最优解为x0,则不存在任何其他解x,使得Zi(x)≥Zi(x0),i=1,2,…,k,其中,至少有一个不等式严格成立。
定义:假设p和q是群体中任意2个不同的个体,若称p支配q,则必须满足以下2个条件:
1)∀m∈{1,2,…,k} ,Ζm(p)≥Ζm(q),即对所有的子目标,p不比q差;
2)∃l∈{1,2,…,k} ,Zl(p)>Zl(q),即至少存在一个子目标,使得p比q好。这里,p为支配的,q为被支配的,可以表示成p≻q。
由于基本蝙蝠算法是用来求解连续域的函数优化问题,所以要将基本蝙蝠算法进行离散化地改进才能求解离散问题。为了将寻优领域控制在0和1 2个整数之间,这里对蝙蝠算法的(2)~(4)进行重新定义:

式中:round指四舍五入取整,xor和or分别指逻辑运算符的异或和或,xold为从当前Pareto最优解集中随机产生的一个解,n指种群个数,d指维数。
下面给出求解多目标0-1规划问题的蝙蝠算法的基本步骤:
1)初始化。蝙蝠种群大小为n,初始种群中第i只蝙蝠位置x(i),速度v(i),脉冲发射速率R(i),脉冲响度A(i),脉冲频率F(i),个体目标函数集Zix i()(),i=1,2,…,n,确定当前Pa⁃reto最优解集。
2)判断是否满足算法结束条件,如果满足,则转9),否则转3)。
3)利用式(1)、(8)、(9)产生一个新的解xnew,并更新速度和位置。
4)if rand>R i()
从当前最优解集中随机选择一个解xold,并利用式(10)得到一个局部解xnew;
endif
5)计算个体目标函数集Zixnew()new。
6)if rand〈A i()&Ζixnew()new〉
Zix i()()
x i()=xnew
Zix i()()=Zixnew()new
通过式(5)减小A i(),式(6)增大R i();
endif
7)更新当前Pareto最优解集。如果xnew支配当前Pareto最优解集的一个或几个解,则将被xnew支配的所有解移出当前Pareto最优解集,而将xnew移入当前Pareto最优解集;如果xnew与当前Pareto最优解集不存在任何支配关系,则直接加入到当前Pareto最优解集中;其他情况则保持当前Pareto最优解集不变。
8)转2)。
9)输入所求的Pareto最优解集。
从算法的流程可以看出,所提算法的时间复杂度大小取决于Pareto最优解集的构造和产生办法。本文选取的是排除法,其时间复杂度为:O kN()。故所提算法的时间复杂度为:O dknN()。其中,d为变量的维数,k为目标函数个数,n为群体个数,N为Pareto最优解集的容量。需要指出的是:下文中,由于所求问题的规模较小,所以并没有给出其具体值,所以在运行过程中,N的值是动态变化的。
3 数值实验
为了验证本算法的性能,分别与遗传算法、蚁群算法[1]、元胞蚁群算法[6]、蜂群算法[7]和粒子群算法[8]进行试验比较,采用文献[9]中4个多目标0-1规划问题进行测试。参数设置为:蝙蝠个数为20,Fmax=1,Fmin=0,α=γ=0.9,初始频率和初始速度均为0,脉冲的响度和发射速率从[0,1]随机产生。环境为Win7系统下的MATLAB 7.8(R2009a).计算结果见表1~表5。
算例1:

试验结果见表1。
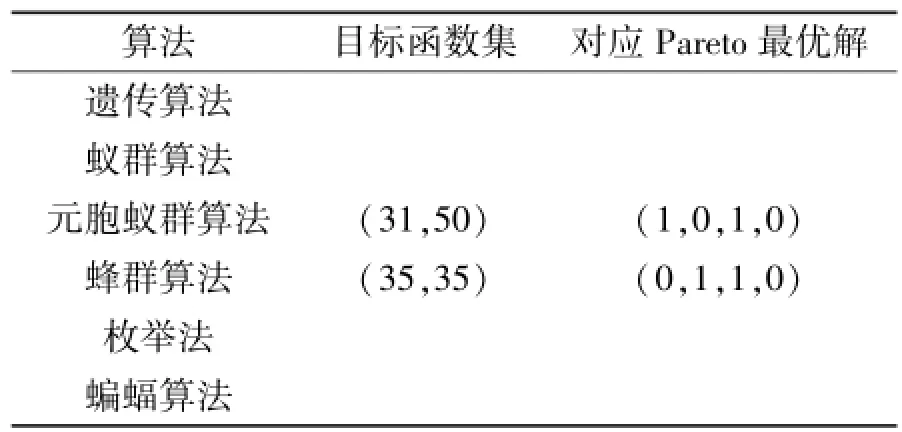
表1 测试1的结果比较Table 1 Comparing resu lts of test 1
算例2:

试验结果见表2。
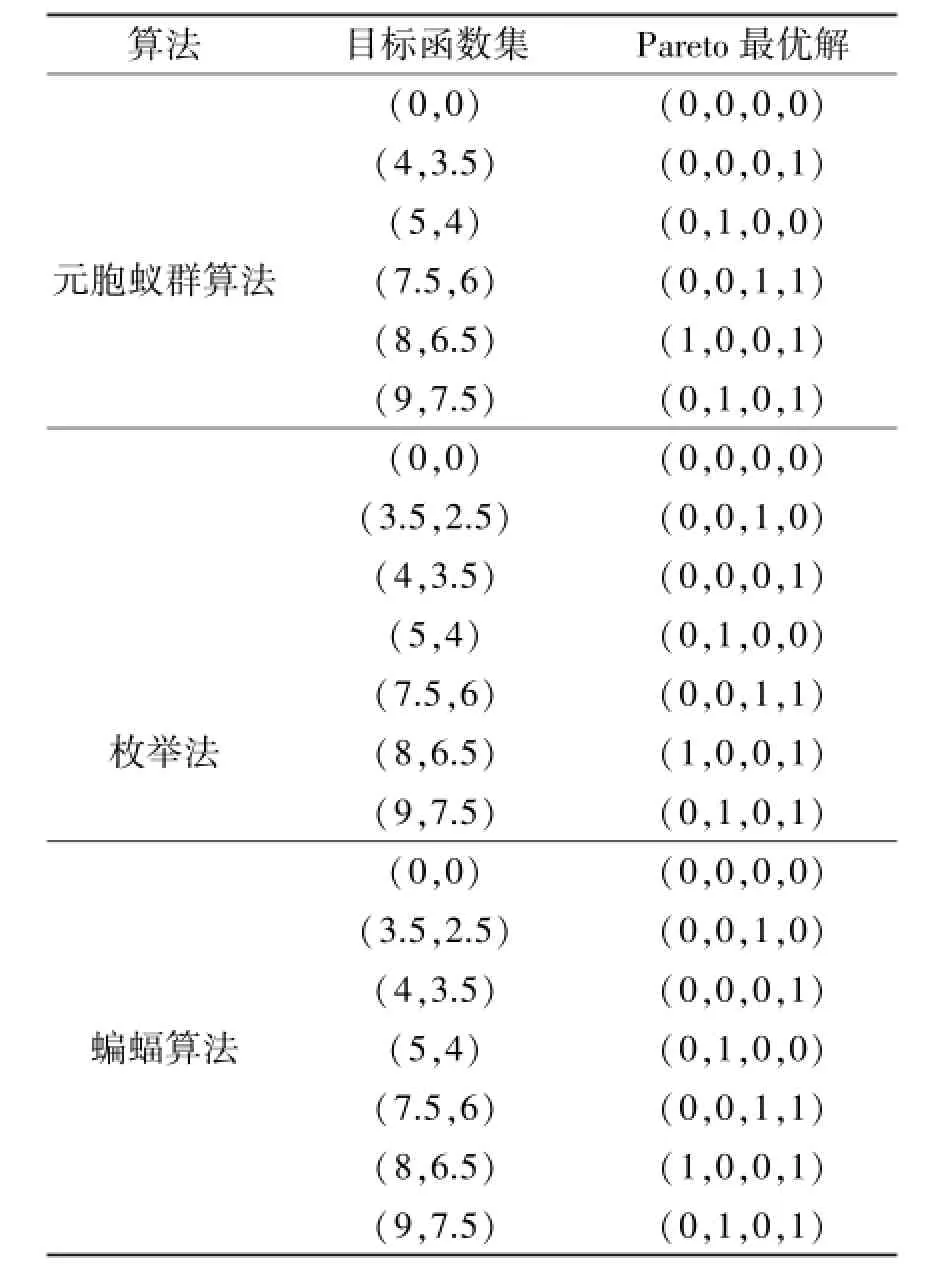
表2 测试2的结果比较Table 2 Com paring resu lts of test 2
算例3:

用蝙蝠算法解得Pareto最优解见表3。对比结果分析见表4。

表3 测试3的结果Tab le 3 Result of test 3

表4 测试3的结果比较Table 4 Com paring resu lts of test 3
算例4:

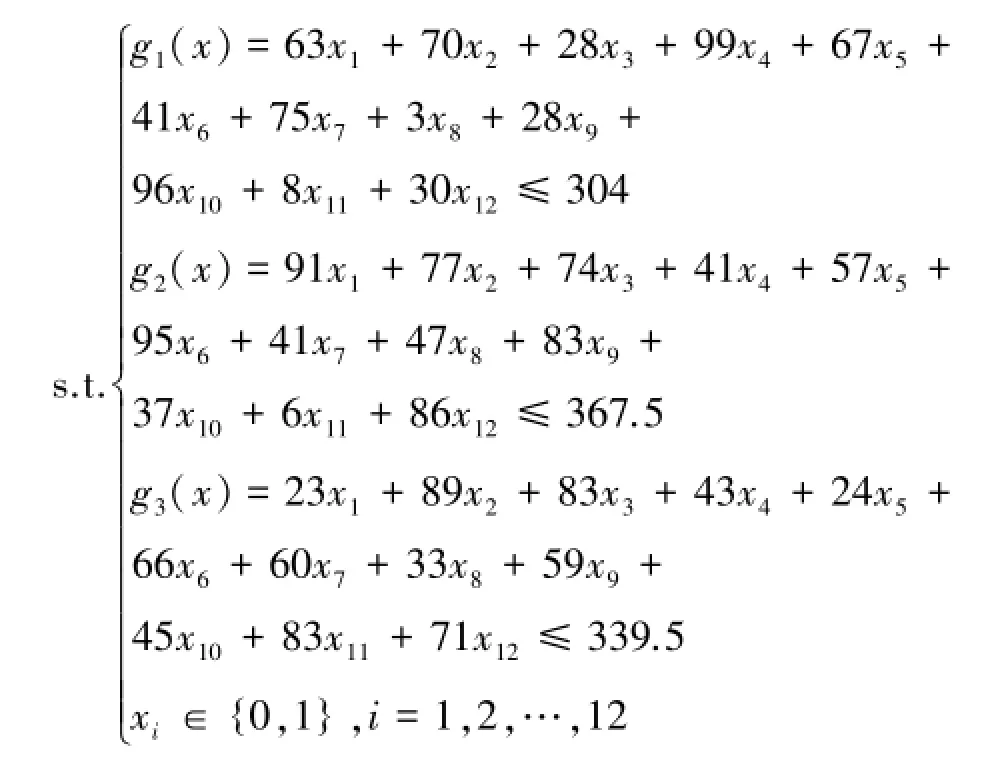
试验结果见表5。

表5 测试4的结果比较Table 5 Com paring results of test 4
通过观察和分析上述4个算例的测试结果,不难发现:文中所提出的算法能够找到上述4个算例的所有Pareto最优解,而遗传算法、蚁群算法、元胞蚁群算法、蜂群算法和粒子群算法却不能保证找到上述4个算例的所有Pareto最优解,从而突出了文章所提出的算法性能的优越性。
4 结束语
蝙蝠算法是一种元启发式算法,启发于微型蝙蝠利用回声定位功能寻找食物、避开障碍物这一特殊现象。从实验结果来看,它比目前应用广泛的蚁群算法、蜂群算法、遗传算法、元胞蚁群算法和粒子群算法具有更好的适应性。文章所提的算法是对多目标规划问题的一种新的尝试,更多的工作尚待于进一步展开,诸如将其应用扩展到多目标整数规划中去,以及其他的经典组合优化问题中去,从而丰富蝙蝠算法的应用领域。
[1]马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008:185⁃189.
[2]YANG X S.A new metaheuristic bat⁃inspired algorithm[M]//Nature inspired cooperative strategies for optimiza⁃tion(NICSO 2010).Berlin Heidelberg:Springer,2010:65⁃74.
[3]YANG X S.Bat algorithm for multi⁃objective optim isation[J].International Journal of Bio⁃Inspired Computation,2011,3(5):267⁃274.
[4]YANG X S,GANDOMI A H.Bat algorithm:a novel ap⁃proach for global engineering optimization[J].Engineering Computation,2012,29(5):267⁃289.
[5]GANDOMIA H,YANG X S,ALAVIA H,et al.Bat algo⁃rithm for constrained optimization tasks[J].Neural Compu⁃ting and Applications,2013,22(6):1239⁃1255.
[6]刘勇,马良,许秋艳.多目标0⁃1规划问题的元胞蚁群优化算法[J].系统工程,2009,27(2):119⁃122.LIU Yong,MA Liang,XU Qiuyan.Solving multi⁃objective 0⁃1 programming by cellular ant algorithm[J].Systems En⁃gineering,2009,27(2):119⁃122.
[7]韩燕燕,马良,赵小强.多目标0⁃1规划问题的蜂群算法[J].运筹与管理,2012,21(2):23⁃26.HAN Yanyan,MA Liang,ZHAO Xiaoqiang.Bee colony al⁃gorithm for the multi⁃objective 0⁃1 programming problem[J].Operations Research and Management Science,2012,21(2):23⁃26.
[8]孙滢,高岳林.一种求解多目标0⁃1规划问题的自适应粒子群算法[J].计算机应用与软件,2009,26(12):71⁃73.SUN Ying,GAO Yuelin.An adaptive particle swarm optimi⁃zation algorithm for solvingmulti⁃objective 0⁃1 programming problem[J].Computer Application and Software,2009,26(12):71⁃73.
[9]杨玲玲,马良,张惠珍.多目标0⁃1规划的混沌优化算法[J].计算机应用研究,2012,29(12):4486⁃4488.YANG Lingling,MA Liang,ZHANG Huizhen.Chaotic opti⁃m ization algorithm formulti⁃objective 0⁃1 programm ing prob⁃lem[J].Application Research of Computers,2012,29(12):4486⁃4488.

李枝勇,男,1986年生,硕士研究生,主要研究方向为智能优化、系统工程。发表学术论文9篇。

马良,男,1964年生,教授,博士生导师,主要研究方向为智能优化、系统工程。先后承担完成包括国家自然科学基金在内的各类科研项目20多项,发表论文300余篇,出版专著1部,主编教材2部。
Bat algorithm for themulti⁃objective 0-1 programm ing problem
LIZhiyong,MA Liang,ZHANG Huizhen
(School of Management,University of Shanghai for Science and Technology,Shanghai200093,China)
Obtainingmore Pareto solutions is very important for the multi⁃objective problem.This paper presented an improved bat algorithm for solving themulti⁃objective 0-1 programming problem with linear constrains.The pro⁃posed algorithm,which is based on redefining the updating formulas of the velocity and position aboutevery bat,is implemented through several tests.The algorithm is compared with a genetic algorithm,an ant colony optimization algorithm,a cellular ant colony algorithm and a particle swarm optimization algorithm.The comparisons showed that the proposed algorithm can getmore Pareto solutions and bemuch more effective to solve such problems.
intelligent optimization;combinatorial optimization;multi⁃objective 0-1 programming problem;batal⁃gorithm
TP301.6;N945
A
1673⁃4785(2014)06⁃0672⁃05
李枝勇,马良,张惠珍.多目标0-1规划问题的蝙蝠算法[J].智能系统学报,2014,9(6):672⁃676.
英文引用格式:LI Zhiyong,M A Liang,ZHANG Huizhen.Bat algorithm for the multi⁃objective 0-1 programm ing problem[J].CAAI Transactions on Intelligent System s,2014,9(6):672⁃676.
10.3969/j.issn.1673⁃4785.201310038
http://www.cnki.net/kcms/doi/10.3969/j.issn.1673⁃4785.201310038.htm l
2013⁃09⁃12.
日期:2014⁃09⁃30.
上海市一流学科建设基金资助项目(S1201YLXK);上海高校青年教师培养资助计划资助项目(slg12010);高等学校博士学科点专项科研基金联合资助课题资助项目(20123120120005);上海市教育委员会科研创新基金资助项目(14YZ090);上海市研究生创新基金资助项目(JWCXSL1202);上海理工大学博士科研启动基金资助项目(1D⁃10⁃303⁃002).
李枝勇.Email:lizhiyong.2180869@163.com.
