基于改进遗传算法的电力系统动态无功优化研究

黄容容 魏金成 陈 勇

（西华大学电气工程学院，成都 610039）

电力系统动态无功优化分析是对调度周期内的系统进行实时无功优化，通过调节发电机组的出力、改变变压器的分接头、确定合理 的无功 补偿 容量和合理的无功 补偿 地点等措施来保证系统的电压水平，最大限度的减少系统的网损，提高供电的经济性[1]。

针对电力系统动态无功优化问题自身的复杂性：在系统运行过程中，控制设备运行状态的改变都将引起电网无功功率的重新分配，从而使系统的有功网损也发生相应的变化。必须要寻找一种全局优化算法来对整个电力系统进行全局优化。多年来，国内外的许多学者针对电力系统无功优化的问题，提出了大量的优化算法，诸如粒子群算法[2]、TS 算法、量子进化算法、内点法、模拟退火算法及遗传算法[3]。遗传算法鲁棒性能强，收敛速度与问题的规模无关且具有广泛的适应性，省去了传统优化方法求解过程中的复杂的数学运算。本文将遗传算法应用于电力系统无功优化的求解，对基本遗传算法作出相应的改进，以达到能够快速准确的求出优化最优解。

1 动态无功优化的数学模型

电力系统动态无功优化通常是依照控制设备的动作次数约束将负荷预测得到的梯形图分成几个大时段，只有在各个大时段之间控制设备才能动作。这就与控制设备动作次数有限形成了严重的矛盾。控制设备在时间和空间上均存在强烈的耦合关系。综合考虑动作次数和准确性两方面的因素，本文将系统的日负荷曲线按小时分成24 段，近似认为每段负荷保持不变，这样就将动态优化转化成静态无功优化进行求解，得到全天动态无功优化模型[4]。

动态优化的目标函数：

等式约束条件：

不等式约束条件：

式中，V=[V1，V2，…，V24]T为24 个时段内各母线电压构成的矩阵；Vt为第t个时段内的NB维母线电压构成的行矢量；C=[C1，C2，…，C24]T为24 个时段内的所有电容器组构成的矩阵；Ct为第t个时段内的p维补偿容量值构成的行矢量；T=[T1，T2，…，T24]T为24 个时段内各有载变压器的分接头档位构成的矩阵；T为第t个时段内的q维档位值构成的行矢量；QG,t为第t个时段内发电机发出无功构成的行矢量；SC为全天之内所有电容器组的动作总次数；p为系统中电容器的总组数；ST为全天之内所有的有载变压器的分接头的动作总次数；q为系统中有载变压器的总台数。

2 应用于无功优化的遗传算法改进

为了遗传算法更加适合应用于电力系统无功优化分析，本文做了相应的改进。

2.1 编码的改进

根据无功优化控制变量的连续和离散都有的特点，本文采用混合编码方式。发电机的机端电压为连续变量，对其采用实数编码，实数编码精度高，便于大范围搜索，同时实数编码在运算过程中不存在解码操作，具有很高的计算精度。有载变压器的分接头和无功补偿装置的投切组数均属于离散变量，对其采用整数编码[5]。两类变量均在其自身允许范围内进行取值。

综上所述，控制变量的编码可以用下式表示：

式中，Tt表示有载变压器的分接头档位；VG表示发电机的机端电压；QC表示无功补偿器的容量；i表示所有发电机节点；j表示可调变压器的数目；k表示所有的无功补偿节点数。

采用上述混合编码方式，使编码的长度与变量的个数保持一致，不仅很好地克服了二进制编码串长的缺点，而且很好地保留了实数和整数编码的优点，进一步提高了遗传算法在电力系统无功优化中的实用性。

2.2 适应度函数的改进

根据不同的评价要求，遗传算法适应度函数的设计具有多样性，为了提高无功优化中遗传算法的优化的速度和计算结果的精度，在进化的不同阶段采取不同的适应函数。

在遗传进化的早期阶段，算法主要是对整体目标的最优区域进行搜索，适应度函数可以设计为

当算法进行到一定阶段之后，主要目标是寻求目标函数在满足约束条件下的最优解，因此，这一阶段要淘汰那些不满足约束条件的个体，表现在适应度函数上就是要增大那些不满足约束条件个体的惩罚因子，适应度函数可以设计为

通过上述分阶段适应度函数进行搜索运算，不断能够提高运算的速度，使最优解的精度也得到很大的提高。

2.3 收敛判据的改进

遗传算法的收敛准则在优化过程也是至关重要的，如果仅仅以遗传代数作为收敛判据，代数设定过小，就会陷入局部最优而得不到预想的全局最优解；遗传代数设定太大，那么当最优解在设置的最大遗传代数之前出现时，就不能保证算法快速收敛而浪费计算时间。针对上述情况，采用最优解最少保持代数np和最大遗传代数m相结合的收敛准则，在预先设定的最大遗传代数范围内，搜索全局最优解，并且当最优解在以后的np次迭代过程保持不变，则输出该最优解，退出优化过程；如果在m代内没有搜索到最优解，则就输出此时的次优解。两种方法的有效结合，既保证了优化过程的全局性，又克服了单一准则的不足。改进遗传算法求解无功优化问题如图1所示。

图1 改进遗传算法求解无功优化问题流程图

3 仿真分析

3.1 算法的验证

为了对改进算法的正确性进行验证，采用IEEE30节点系统进行仿真。将仿真结果同基本遗传算法进行比较。

IEEE30节点系统包括6台发电机（1,2,5,8,11，13），4台可调变压器（4-12，6-9，6-10，28-27），2个无功补偿节点（10,24），其基本参数可参考文献[22]，种群规模取成50，遗传代数的最大值取为100。基本算法的参数为：pc=0.65，pm=0.095；本文参数为pc0=0.85，pcstep=0.0015，pcmin=0.08；最优个体的保留代数设置为np=8。变压器的变比上下限均选为0.90～1.10，调节档位为1.0±6×2.5%，共分成13档，限制每次的实际调节档数小于等于3。发电机机端电压的上下限取为0.90～1.10p.u.，其他节点取电压的上下限为0.95～1.05p.u.，除1为平衡节点外，其他发电机节点规定为PV节点，剩余节点规定为PQ节点。

本文为了优化时有足够的无功备用容量，增加了3 个（15，26，30）无功补偿节点，取节点1 为平衡节点，系统有功负荷总和为2.834pu，无功负荷的总和为1.262，SB=100MVA。由于算法具有随机性，对两种算法均进行10 次运算，取各自最好的结果进行对比。

两种算法优化结果的比较见表1。

表1 两种算法结果比较(p.u.)

从表1可知，改进遗传算法的有功损耗以及有功损耗降低率都有所提升，计算速度提高了两倍多，验证了本文改进遗传算法的切实可行性。

3.2 动态无功优化实例分析

1）负荷曲线的分段

成都大邑县电业局2013年3月2日的负荷预测值，利用积分中值定理将负荷预测曲线按一天24h进行分段，将分段负荷曲线进行归一化处理，得到如图2所示的柱状图，并以IEEE30节点系统的给定负荷作为基准负荷，形成IEEE30节点系统的全天动态无功优化模型。

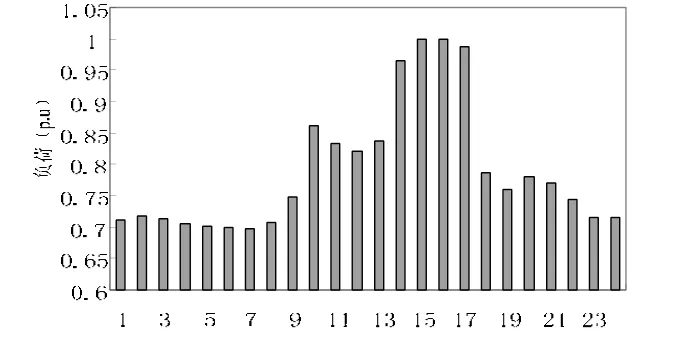
图2 归一化分段负荷曲线

2）动态无功优化仿真分析

利用改进的遗传算法对分段负荷曲线的全天24段分别进行静态无功优化计算，计算出各控制变量的值，结合各控制变量的动作次数约束分配动作时刻。

本文以15 号节点选出最大的5 个时刻为例来动态演示控制设备的动作时刻变化。如图3所示。

图3（a）所示是利用改进的遗传算法对每一段进行静态无功优化计算，求得每一段的无功补偿容量和控制设备的动作值，考虑控制设备的动作次数 约束，初步确定的控制设备的动作时刻表。

图3（b）所示是在保证第一段最优的情况下，对后续时段分别进行动态优化，根据各时段控制设备的差值重新调整动作时刻表。

图3（c）所示是为了满足电力系统在大负荷是有充足的无功补偿量，采用负荷因子对动作时刻表进行调整，重新分配控制设备动作时刻表，达到从整体上对系统进行优化。

对比图3（a）和图3（b），电容器组的动作时刻发生了重置，但图3（b）采用的是在等权重的前提下保证每段网损尽量最小的方法。由于差值变化很小，在负荷很大时无功补偿不足，而在负荷较小时无功补偿又过剩。为了避免这一缺陷，满足实际电网运行的要求，本文引入负荷因子，比较图3（b）和图3（c），在负荷达到最大值的16时，图3（c）分配控制设备动作权限，更贴近实际运行的要求。

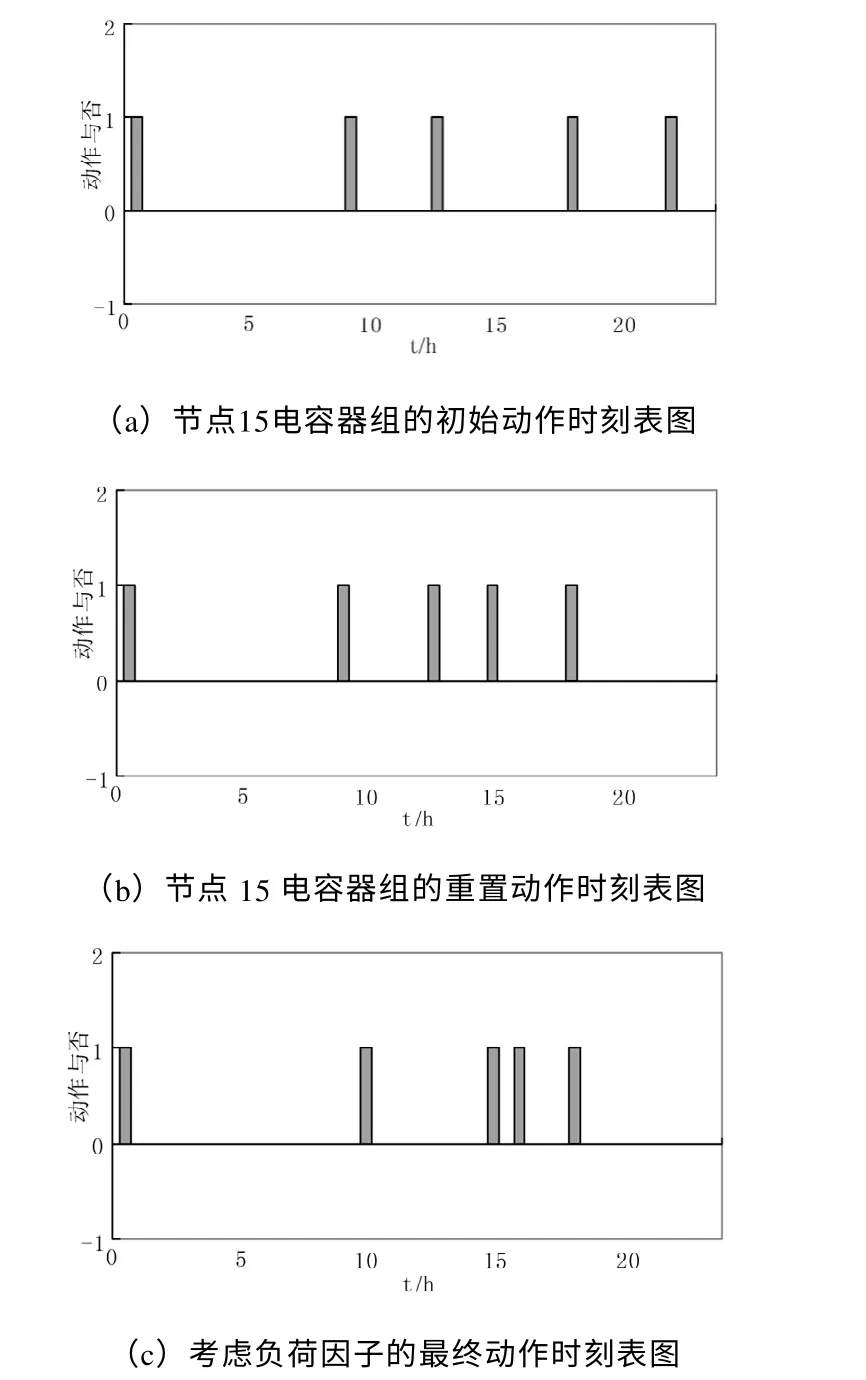
图3 节点15 电容器组的动作时刻表图

电力系统动态无功优化分析的前提是保证系统的电压水平。如图4所示，给出了发电机机端电压的变化值。

从上面的图中可以发现，发电机均在 0.9～1.10p.u 之间，满足电压合格率的要求。

如表2所示给出了动态无功优化的网损变化及各时段控制设备的动作数。该动态优化的方法在每时段降低网损的效果明显，有效地将控制设备动作次数离散化且减少了控制设备的动作次数。

通过对控制设备动作时刻表和发电机机端电压的分析，验证本文的算法能够满足电网动态无功优化的要求，很好地提高了电压合格率，合理分配动作设备动作时刻，能够满足实时电网优化的要求。 差在0.5Hz时，补偿后的电压和电流的偏差已经基本允许范围，若误差再大则不能满足正常运行的要求，可以得出范围为±0.5Hz。

图4 发电机机端电压曲线图

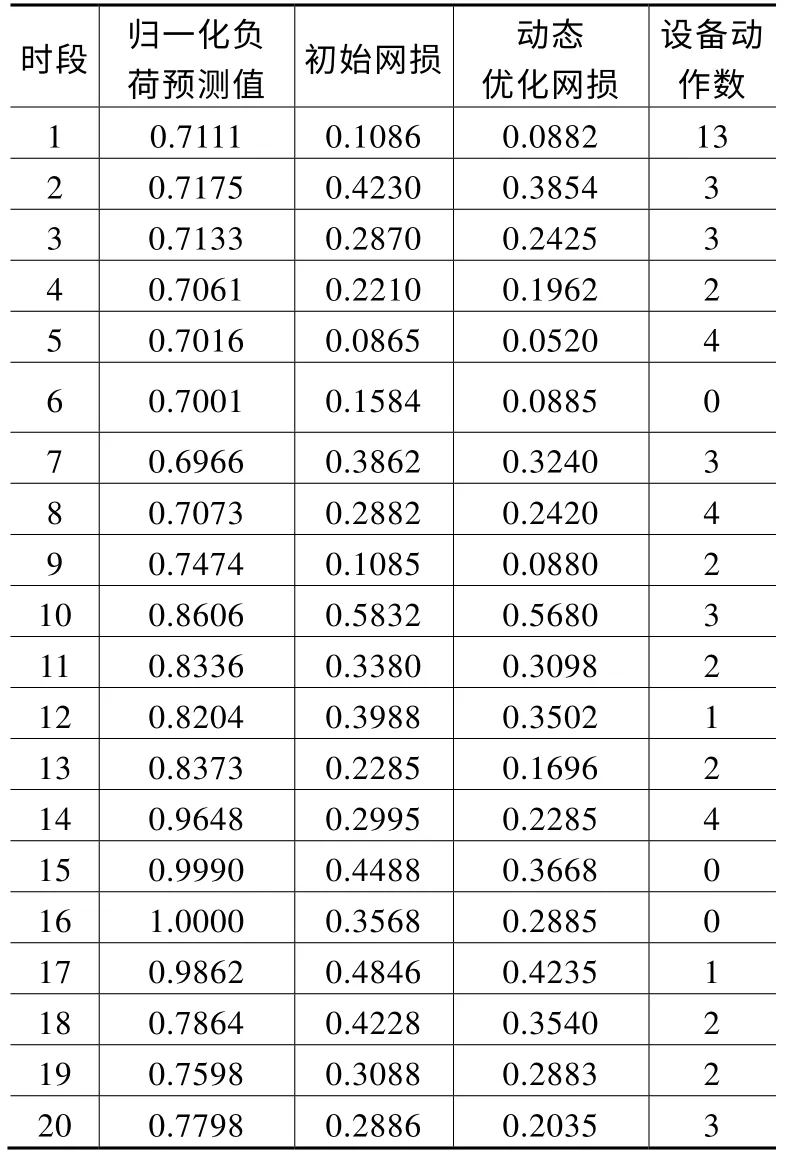
表2 网损变化及设备动作次数

4 结论

本文结合有源滤波的思路，提出了一种新型的铁磁谐振防治措施，在系统的易发生铁磁饱和的器件进行实时的监控，对能够引起饱和的大电流进行有源滤波，使得谐振电路不能形成，在理论上，可以有效防治铁磁谐振过电压的产生。使得谐振中必备的铁心铁磁饱和的运行状态进行控制，使之工作在正常的工作状态，在理论上，本方案是最好的，通过仿真我们也可以看出，我们对补偿的精度要求是十分高的，在相位上的精度是±10°，在频率上式±0.5Hz。所以我们需要进一步根据该思路进行进一步的探索，使得我们的方案在硬件上能够实现。同时本文利用ATP 仿真，验证该消谐措施的正确性和存在的问题进行了仿真预判。

根据本课题的特点，还有不少问题有待进一步研究：

1）我们还需要做更多的物理模拟仿真实验，得到更多的现场数据对我们提出的方案进行佐证。这样我们对铁磁谐振的分析才更有说服力。

2）有仿真可以看出，基于有源滤波的主动补偿消谐的新思路存在的问题，其补偿的精度要求十分高，要是补偿控制没达到要求，防治效果可能适得其反。

[1] 解广润.电力系统过电压[M]. 北京:水利电力出版社,1985.

[2] 平绍勋.电力系统内部过电压保护及其实例分析[M].北京:中国电力出版社,2004.

[3] 陈维贤.内部过电压基础[M].北京:北京电力工业出版社,1981.

[4] 胡成.配电网的铁磁谐振机理和消谐措施的研究[D].西南交通大学硕士毕业论文,2010.

[5] 周小梅.配电网铁磁谐振抑制措施的研究与分析[D].华北电力大学硕士毕业论文,2008.

[6] 许志龙,黄建华,王大忠.10kV 电网TV 铁磁谐振过电压数字仿真及研究[J].电力自动化设备,2001(2).

[7] 周浩,余宇红,张利庭,等.自动跟踪补偿消弧线圈装置的原理和应用[J].电网技术,2005(11).

[8] ZHANG H,XU Y Q,WANG Z P. Research on a new extinction coil operation mode for resonant earthed neutral system.2006 International Conference on Power System Technology.

[9] LI L S,JIANG L P. Study on line detection and fault location with automatic track arc suppression coil device[C]. 2006 International Conference on Power System Technology.

[10] 曾祥君,许瑶,陈博,等.中性点不接地配电网电容电流实时测量新方法[J]. 电力系统自动化学报,2009(2).

[11] 曾祥君,刘张磊,马洪江,等. 配电网电容电流实时测量技术[J].电力系统自动化,2008,32(3).

[12] WEI X X,JI Y CH,WANG J Z,MU X M. Study on new type orthogonal arc-suppression coil of ground fault protection. 2006 International Conference on Power System Technology.