一类单自由度齿轮系统动力学特性分析

史建文，王 楠，李晓蕾

（兰州交通大学数理学院，甘肃兰州730070）

一类单自由度齿轮系统动力学特性分析

史建文，王 楠，李晓蕾

（兰州交通大学数理学院，甘肃兰州730070）

摘要：建立了考虑齿侧间隙、时变啮合刚度等因素下的单自由度齿轮系统非线性动力学模型，采用变步长Runge-Kutta法对系统运动微分方程进行数值求解.结合系统的分岔图、Lyapunov指数图、相图、庞加莱映射图、时间相应图，分析系统随阻尼比变化时的动力学特性和啮合刚度对系统的影响，得到系统的混沌运动形成过程.结果表明，随着阻尼比变化，系统表现出丰富的动力学特性，同时啮合刚度影响系统的分岔点位置.

关键词：非线性动力学；分岔；齿轮；阻尼比；啮合刚度

齿轮传动是现在使用非常广泛的一种传动装置，研究齿轮系统的动力学特性具有重要的理论价值和工程意义.目前，国内外学者已经做了大量的研究工作，Kahraman等［1］建立考虑误差激励、齿侧间隙的单级齿轮系统动力学模型，研究系统的混沌响应和次谐响应.王三民等［2］考虑时变刚度、轮齿间隙和摩擦，建立了单自由度直齿轮传动系统动力学模型，并研究摩擦对系统动力学行为的影响.王立华等［3］利用庞加莱映射、相平面研究包含时变啮合刚度和间隙的单自由度齿轮传动系统动力学模型.随着齿轮系统理论知识不断发展、完善，近年来大量学者把齿轮的工程背景考虑在内，建立许多具有工程意义的模型［4］.大部分的研究都是借助数值方法探讨系统分叉、混沌等现象的存在.本文以单自由度齿轮副非线性动力学模型为研究对象，采用数值模拟方法，研究阻尼比和啮合刚度对系统动力学特性的影响.

1 齿轮副非线性动力学模型及其运动微分方程

仅考虑轮齿的扭转振动，忽略支承系统的弹性变形以及传动轴的横向和轴向弹性变形等因素，采用集中质量法建立了如图1所示的齿轮副非线性模型［5］.

图1中θ1、θ2为主、被动齿轮的扭转振动位移；I1、I2为主、被动齿轮的转动惯量；Rb1、Rb2为主、被动齿轮的基圆半径；cg为齿轮副的啮合阻尼；e（t）为齿轮副的啮合综合误差；k（t）为齿轮副的啮合综合刚度；T1、T2为作用在主、被动齿轮上的转矩.

根据牛顿第二定律，可得到系统的运动微分方程：

为了消除刚体位移并将系统进行无量纲化处理，引入齿轮啮合线上的相对位移作为广义坐标：

将方程（3）转化为状态方程：

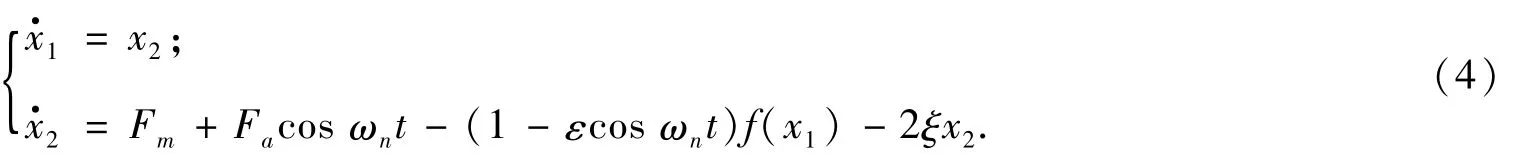
Fa为齿轮传动的外部激励幅值，ε为齿轮啮合刚度.Fm为齿轮传动的等效外部激励，动载荷为P＝（1-εcf（x1））.

2 非线性特性数值仿真分析

2.1 阻尼比对系统的影响

选取参数ε＝0.1，Fm＝0.05，Fa＝0.1，ωn＝1.5，初值x1＝0，x2＝0，齿侧间隙＝0.5.系统随阻尼比ξ变化的分岔图和Lyapunov指数图如图2～3.

图2～3可以看出，阻尼比ξ∈［0.056 1，0.25］时，Lyapunov指数为负，系统处于周期状态，当时系统运动为稳定的周期一运动，当ξ＝0.137 1时系统运动经倍化分岔为二周期运动，当ξ＝0.077 2时二周期变为四周期运动，ξ＝0.058 7时四周期变为八周期运动.此后，随着ξ的增大，当ξ∈［0.030 5，0.056 1］时，Lyapunov指数为正，系统经倍化分岔进入混沌状态.ξ∈［0.000 7，0.030 5］时，Lyapunov指数为负，系统由混沌退化为三周期运动，ξ＝0.017 1时经倍化分岔由三周期变为六周期运动.当ξ∈［0，0.000 7］时，Lyapunov指数为正，系统又进入混沌状态.图4～8为阻尼比ξ取不同值时的相图、庞加莱截面图和时间相应图.

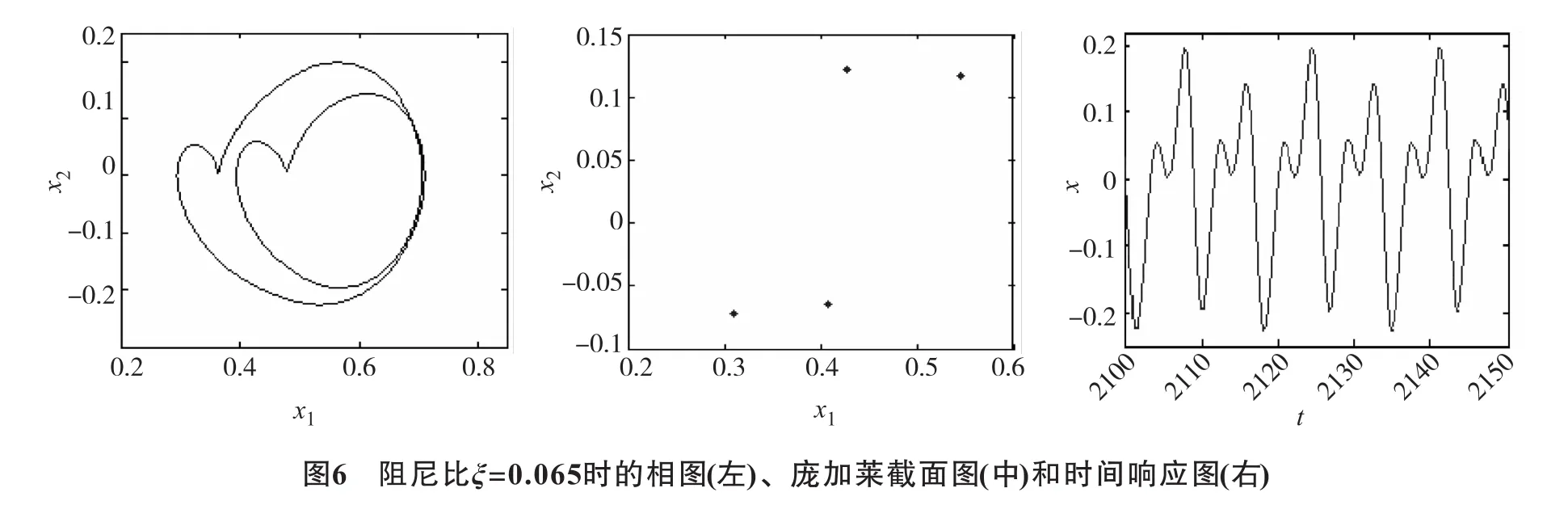
2.2 刚度对系统的影响

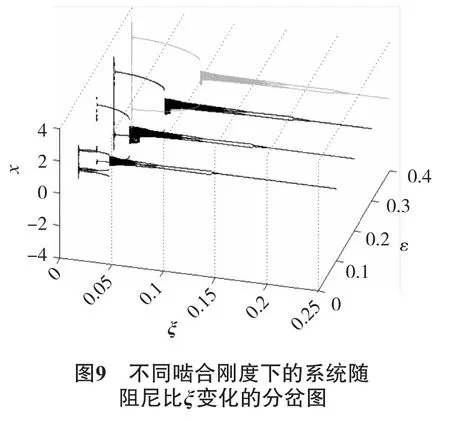
其他参数保持不变，分别取啮合刚度ε＝0.1、0.2、0.3和0.4，分别画出了系统随阻尼比变化的分岔图，将4个分岔图放在同一坐标系下，如图9所示.当ε＝0.1时，系统分岔点为阻尼比ξ＝0.137 1，随着啮合刚度ε逐渐增大，当ε＝0.4时，系统分岔点变为ξ＝0.218 2.同时.随着ε逐渐增大，混沌区域越来越大.因此，在其他参数值不变的情况下，啮合刚度ε越大，系统的分岔点也就越大，系统表现出更加丰富的动力学行为.

3 结语

利用变步长Runge-Kutta法对单自由度齿轮系统运动微分方程进行数值求解，给出系统随参数变化的分岔图，结合Lyapunov指数图、相图、庞加莱映射图以及时间相应图，分析系统随阻尼比变化时复杂的动力学行为.同时，在其余参数保持不变时，随着啮合刚度逐渐变大，系统分岔点越来越大，混沌区域越来越大，因此，在其他参数值不变的情况下，啮合刚度ε越大系统的分岔点变大，系统表现出更加丰富的动力学行为.

参考文献：

［1］KAHRAMA N A，SINGH R.Non-linear dynamics of a spur gear pair［J］.

Journal of Sound and Vibration，1990，142（1）：49-75.

［2］王三民，沈允文，董海军.含摩擦和间隙直齿轮副的混沌与分岔研究［J］.机械工程学报，2002，38（9）：8-11.

［3］王立华，李润方，林腾蛟，等.齿轮系统时变刚度和间隙非线性振动特性研究［J］.中国机械工程，2003，14（13）：1143-1146.

［4］JOANNA M，MARTIN H，EDDIE W R.Mathematical models of gear rattle in roots blower vacuum pumps［J］.Journal of Sound and Vibration，2007，308（3／4／5）：431-440.

［5］苏程.单级齿轮传动系统非线性动力学特性分析［J］.兰州理工大学学报，2012，38（1）：32-36.

（责任编辑 梁志茂）

中图分类号：TH132.41

文献标志码：A

文章编号：1672-8513（2014）06-0447-04

收稿日期：2014-02-10.

作者简介：史建文（1985-），男，硕士研究生.主要研究方向：微分方程及应用动力系统.

Analysis of the nonlinear dynamic characteristics of a single-degree-of-freedom spur gear pair system

SHI Jian-wen，WANG Nan，LI Xiao-lei
（School of Mathematics，Physics and Software Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China）

Abstract：A nonlinear dynamic model for a spur gear pair system was established wherein the backlash and mesh stiffness were considered.The nonlinearsingle degree-of-freedom equations were solved by employing the variable step-size Runge-Kutta integration method.The nonlinear dynamic characteristics of the system were discussed concerning different damping ratios based on bifurcation diagrams，Lyapunov exponents andphase portraits，Poincare maps，the time response figure，and mesh stiffness′s effect on the system.The result has showed that along with the changed damping ratio，the system has showed abundant dynamic characteristics，and its mesh stiffness has affected the location of the bifurcation point of the system.

Keywords：nonlinear dynamic；bifurcation；chaos；gear；damping ratio；mesh stiffness