基于强度折减法的三维边坡失稳判据

周元辅，邓建辉，崔玉龙，郑洪春，陈 滔

（1.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065；2.四川大学 水利水电学院，成都 610065）

1 引 言

自从强度折减法运用于边坡稳定分析以来，边坡失稳判据一直是一个争议性的问题。强度折减法最先在二维边坡稳定分析中使用，因此，最初的失稳判据都是基于二维边坡。赵尚毅等[1]提出将非线性有限元计算不收敛作为失稳判据，并将以此判据得到的计算结果与传统极限平衡法相比误差较小，从而得到有限元计算不收敛为失稳判据的合理性。因为导致数值计算的不收敛的原因较多，比如：网格、边界条件或存在奇异点等，所以有学者提出了以位移突变[2－4]作为失稳判据的依据，即坡顶的水平位移增量和强度折减系数的增量变化趋势。然而栾茂田等[5]则提出了以广义塑性应变及塑性开展区作为边坡失稳的评判依据。万少石等[6]对4种判据进行对比分析，发现其相互之间的误差在2%以内。但也有学者认为，塑性区贯通作为边坡稳定判据是一种不够合理的判据[7－9]。位移控制和塑性区贯通联合使用[10－11]就成为一种能够更加准确判断边坡稳定状态的手段。在边坡三维稳定分析中，边坡稳定判据相关研究主要集中在计算不收敛判据[12]、位移突变判据[13－15]及塑性区贯通判据[16]。

在边坡三维分析中由于数值计算模型的复杂性及存在非线性问题等因素都会导致计算不收敛，因此，计算不收敛判据在边坡三维分析中的误差将比二维分析大。联合使用位移突变和塑性区贯通判据因可以相互印证而被大多数人所接受。但在位移突变判据和塑性区贯通判据中存在以下问题：①何种位移类型（分量位移、总位移及增量位移）和折减系数的曲线更易识别突变点及选取哪些监测点才能成为特征点；②怎样减小塑性区贯通判据引起的误差。本文将依托珍珠坝边坡对以上两个问题展开研究。

2 工程概况

珍珠坝边坡位于金沙江右岸云南绥江县南岸乡，距下游电站坝址约 68.7 km。金沙江河道在该滑坡附近为一平面呈“Ω”型的大拐弯，大拐弯附近金沙江左岸有2条较大支流（上游为西宁河、下游为中都河），该边坡地段金沙江流向总体呈南北向。

珍珠坝边坡所在的金沙江大拐弯岸坡为典型单面山地貌，基岩地层岩性为J2s的灰白-灰绿色细砂岩与暗紫-灰绿色钙质泥岩、泥质粉砂岩互层，岩层产状：80°～105°∠13°～18°，山脊最大高程为940.8 m、江水面高程为302.8 m。大拐弯西侧为逆向坡，地形陡峻，平均坡度约50°，其中 650.0 m高程以上沿厚层砂岩发育2～3级10～20 m高的陡坎；大拐弯东侧为顺向坡，地形平缓，平均坡度约为15°（与岩层倾角相当）；大拐弯珍珠坝在金沙江左岸，岸坡为逆向坡，地形和坡度与滑坡地段西侧金沙江右岸逆向坡的特征基本一致。

3 数值模型及参数

本文主要基于FLAC3D进行数值分析，数值模型平面计算范围为 874 m×1050 m，X轴正向为NE5°，坐标范围为 0～874 m；Y轴正向为SE95°，坐标范围为0～1050 m；Z轴为垂直向，坐标与海拔高程相同，范围自高差75 m至地表；坐标平面原点在计算范围的左下角（见图1）。

珍珠坝滑坡的特殊性表现是在河床部位有明确的剪出口。因此，在计算分析时，将滑坡体分为滑体、滑带及滑床。计算考虑了3种主要的地质材料，即滑体、滑带和滑床（基岩）。主要计算参数见表1。计算模型图 1共划分节点为 349608个，单元为329724个。约束边界条件均为位移边界条件，即在x=0.0 m和x=874.0 m边界上施加X向位移约束；在y=0.0 m和y=1050.0 m边界上施加Y向位移约束；在z=75.0 m边界上施加Z向位移约束。为了对位移突变判据分析一共布置了12个监测点，监测点布置图见图1。

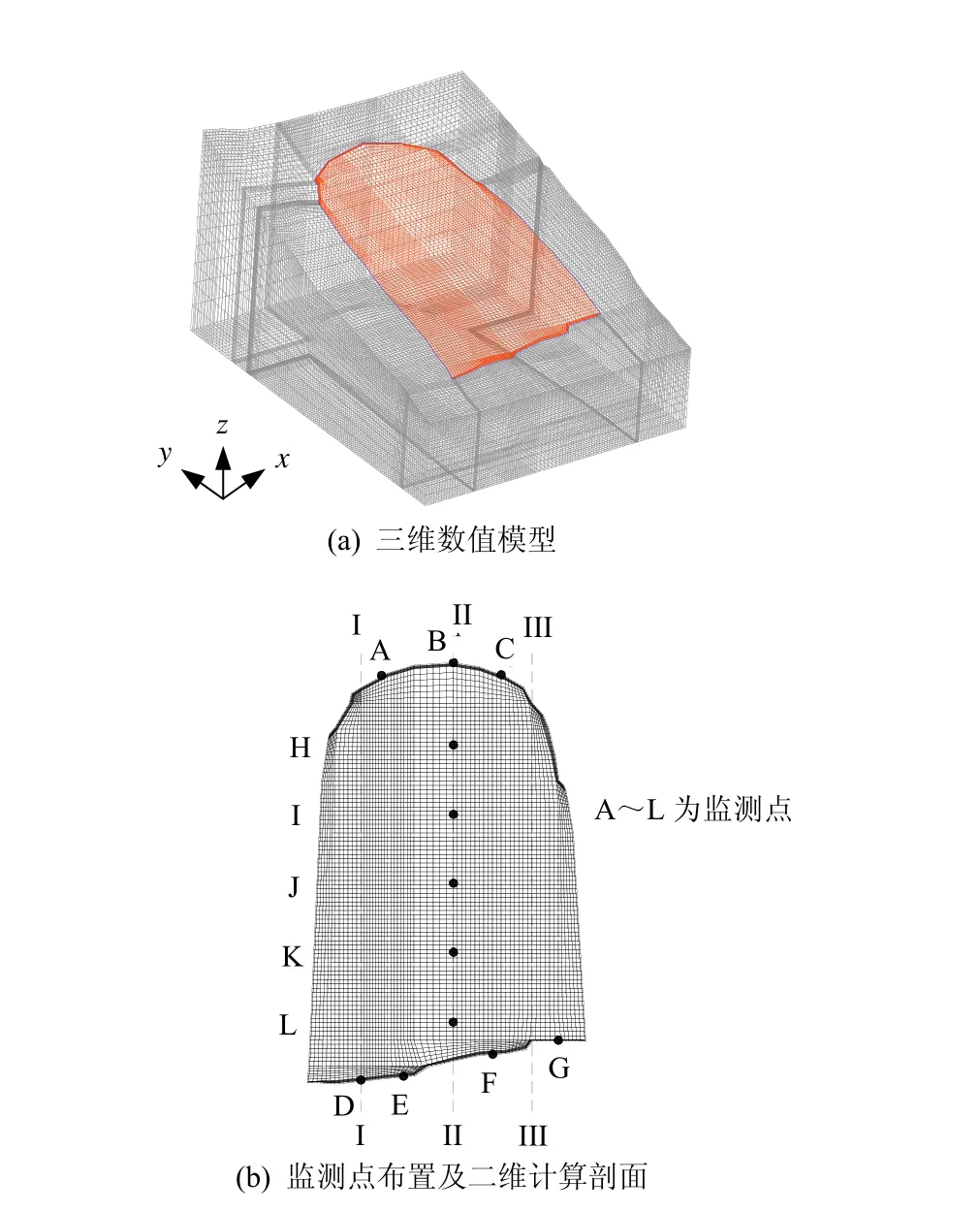
图1 三维数值模型、监测点布置及二维计算剖面位置Fig.1 3D numerical model,distribution of monitoring points and locations of sections for 2D calculation

计算主要分两步进行，第1步计算滑床、滑体和滑带在重力作用下的弹性变形和应力，作为初始状态；第2步先将弹性变形清零，第1步计算的应力作为初始应力。根据强度折减法原理和不同的折减系数所对应的计算参数，重复第2步计算过程直至求得安全系数。因为，此处主要关心滑带塑性区发展，所以此处仅将滑带的材料属性变为弹塑性，模拟变形和破坏发展过程。滑带使用理想弹塑性本构模型、Mohr-Coulomb屈服准则；滑体和滑床使用线弹性模型。安全系数 Fs的实际计算过程是基于式（1）所示的强度折减概念，其他计算参数不进行强度折减：

式中：RF为强度折减系数。

4 位移突变判据分析

本次数值计算强度折减系数从1.00开始按照增量为0.05递增进行计算。从图2～4可以看出，边坡坡顶监测点A～C的X、Y、Z方向的位移均出现有明显的位移突变，而坡脚监测点D～G的X、Y、Z方向的位移相对于坡顶则没有出现明显突变。在总位移和强度折减系数关系曲线（见图 5）中可以看出，坡顶和坡脚位移随强度折减系数的增大的变化规律更加明显。坡顶监测点在强度折减系数为1.25处具有明显的突变点，而坡脚监测点不但没有明显位变点，而且几乎是几条平行的曲线。从总位移增量与折减系数关系曲线（见图 6）可以看出，坡顶监测点位移变化与总位移变化趋势基本一致；而从坡脚也可以看出，当折减系数为1.25时有突变出现，但没有坡顶位移变化明显。从上面分析可以看出，用总位移增量与折减系数关系曲线可以较好地识别出位移突变点。

图2 监测点A～G的X方向位移与强度折减系数关系曲线Fig.2 Curves of X-displacement with strength reduction factors at observation points A-G

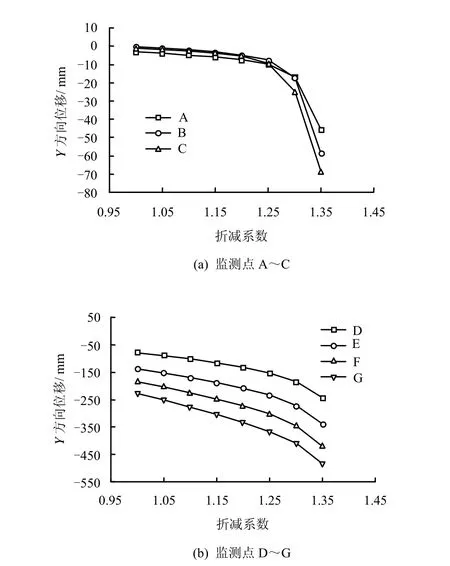
图3 监测点A～G的Y方向位移与强度折减系数关系曲线Fig.3 Curves of Y-displacement with strength reduction factors at observation points A-G

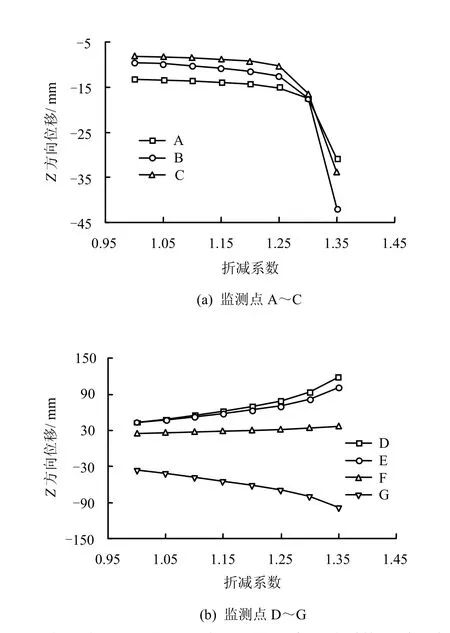
图4 监测点A～G的Z方向位移与强度折减系数关系曲线Fig.4 Curves of Z-displacement with strength reduction factors at observation points A-G

图5 监测点A～G的总位移与强度折减系数关系曲线Fig.5 Curves of total displacement with strength reduction factors at observation points A-G

虽然上述分析表明，坡顶可能成为位移突变特征点的位置，但还不能肯定特征点一定会出现在坡顶。为了分析沿坡顶到坡脚方向不同部位位移随折减系数的变化趋势，根据上述分析，采用总位移增量和折减系数的关系曲线（见图 7）分析特征点位置。从图可以看出，监测点总位移从坡顶到坡脚逐渐增大，位移突变点在曲线上的显现逐渐模糊。同时，从图6可知，在边坡同一横剖面附近比，如监测点A～C、D～G的总位移增量随折减系数变化规律基本一致。因此可以判定，用位移突变判据分析三维边坡稳定时特征点选取在坡顶较为合理。这与通过二维分析得出的位移突变判据基本一致，但为防止误判，建议多取几个监测点以相互印证。

5 塑性区贯通判据分析

塑性区贯通判据认为，塑性区贯通时的折减系数为安全系数。经计算珍珠坝边坡在折减系数为1.35时塑性区全部贯通，即整个滑带均处于塑性状态。根据文献[7－9]，滑带贯通时的折减系数作为安全系数是存在误差的。因此，本文提出以塑性区的贯通率和折减系数的关系来判断三维边坡的临界状态。塑性区贯通率η的定义如下：

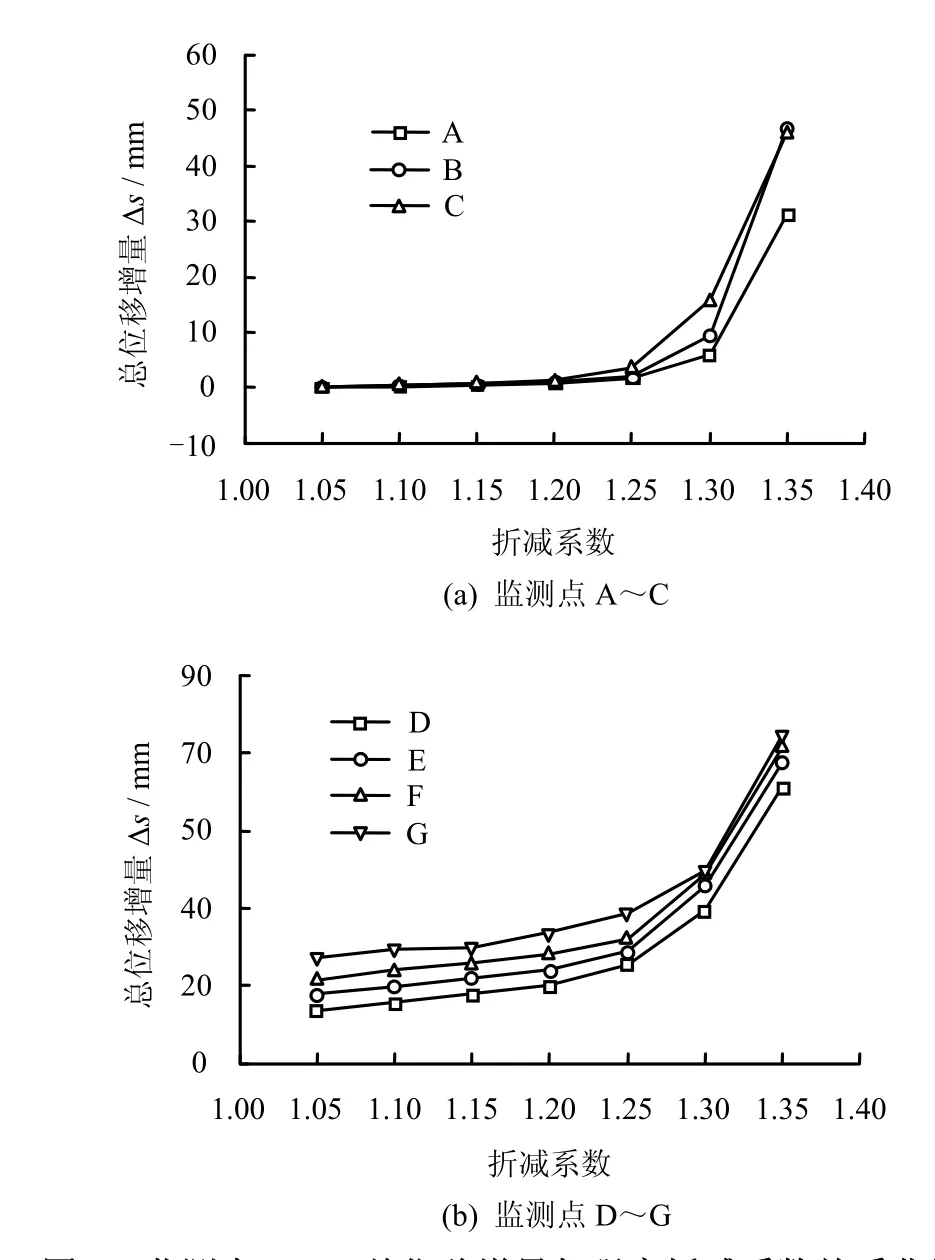
图6 监测点A～G总位移增量与强度折减系数关系曲线Fig.6 Curves of increments of total displacement with strength reduction factors at observation points A-G

图7 监测点B,H～L总位移增量与强度折减系数关系曲线Fig.7 Curves of increments of total displacement with strength reduction factors at observation points B,H-L

式中：η为塑性区贯通率；Vpl、Vtotal分别为塑性区体积和滑带体积；Spl、Stotal分别为塑性区面积和滑带面积。

从图 8(a)可以看出，塑性区的贯通率随折减系数增大而增大，但在折减系数大于1.20以后变化较小。因此，对折减系数在1.10～1.20之间的塑性区贯通率做进一步分析。折减系数从1.10开始按照增量为0.02依次增加，得到塑性区贯通率和折减系数的曲线见8(b)。从该图可以看出，突变点出现在折减系数为1.16处。用塑性区贯通率增量和折减系数的关系曲线（见图 9）可以看出，塑性区贯通率增量突变点出现在折减系数为1.16处。此时塑性区主要分布在边界附近，塑性区贯通率为0.97左右。在这种情况下，整个塑性区已经基本贯通。在边坡边界附近有未处于塑性状态的岩土体出现，主要是由于在边界附近的滑体较薄，但并不代表此时滑坡不是处于危险状态。在现实情况中，滑坡滑动时边界上的部分岩土体也不会处于塑性状态。由于塑性区贯通率增量与折减系数关系曲线中的突变现象较塑性区贯通率与折减系数关系曲线明显。因此，采用塑性区贯通率增量突变作为三维边坡临界状态的判断更加符合实际且具有实用价值。

图8 塑性区贯通率与强度折减系数关系曲线(ANSYS)Fig.8 Curves of penetration rate of plastic zone with strength reduction factors(ANSYS)

图9 塑性区贯通率增量与强度折减系数关系曲线(ANSYS)Fig.9 Curves of increments of penetration rate of plastic zone with strength reduction factors(ANSYS)

6 讨 论

上述分析结果是采用FLAC3D计算，为了验证塑性区贯通判据的可靠性，本文以有限元为理论基础的 ANSYS软件进行对比分析。计算模型采用FLAC3D计算的同一模型。由于ANSYS软件中无Mohr-Coulomb准则（简称 M-C），只有 Drucker-Prager准则（简称 D-P），此处根据文献[17]将ANSYS中的外角点外接D-P与M-C等面积圆D-P等效可以求得相对应的参数，即令表2中的 α1=α2，κ1=κ2就可求得与FLAC3D强度折减过程中的参数等效的 D-P准则计算参数（见表 3）。计算过程与FLAC计算过程一致。

表2 M-C与D-P准则换算公式Table 2 Conversion formulas between criterion M-C and D-P

表3 M-C与D-P准则换算参数Table 3 Conversion parameters between criterion M-C and D-P

图10为FLAC3D与ANSYS同一等效参数下计算的贯通率随强度折减系数增大的趋势图。由此可以看出，二者计算结果趋势基本一致。当强度折减系数大于1.15时变化较小，且此时塑性区贯通率在0.95以上。图11为强度折减系数在1.10～1.20之间的塑性区贯通率增量随强度折减系数变化的趋势图。从该图可以看出，当强度折减系数为1.16时，FLAC与ANSYS计算结果均出现了突变点。从强度折减系数为1.16时的塑性区分布图（见图12）可以看出，此时塑性区在整个滑带基本贯通。因此，用塑性区贯通率增量判据可得该滑坡安全系数均为1.16，由此可以证明该判据是可靠的。

图10 塑性区贯通率比较（ANSYS和FLAC法）Fig.10 Comparison of penetration rate of plastic zone between ANSYS and FLAC

图11 塑性区贯通率增量比较（ANSYS和FLAC法）Fig.11 Comparison of increments of penetration rate of plastic zone between ANSYS and FLAC

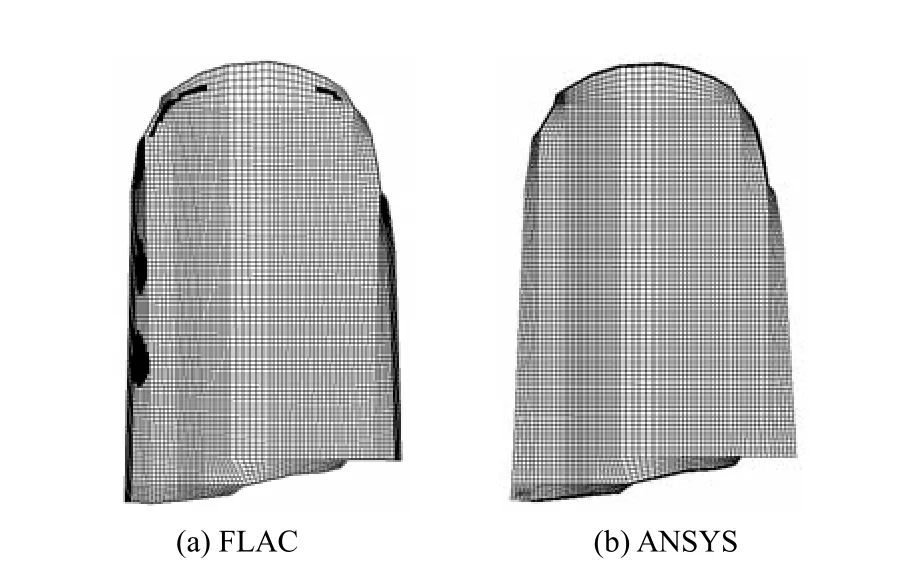
图12 强度折减系数为1.16时的塑性区分布图Fig.12 Distribution of plastic zone when strength reduction factor is 1.16

传统的极限平衡法计算安全系数由来已久，也已广泛运用于边坡稳定分析中。因此，本文又选取了3个剖面（剖面位置分布见图1）进行了二维极限平衡分析，计算结果与三维计算结果对比见表4。从表4中二维安全系数可以看出，滑带左侧安全系数较中部和右侧大，这与三维计算结果（图12）一致。若将二维计算中安全系数最小值作为整个滑坡的安全系数，3种方法计算所得安全系数基本一致为1.24。三维计算中采用监测点总位移增量突变判据、塑性区全部贯通判据及塑性区贯通率增量突变判据时的安全系数分别为1.25、1.35及1.16。塑性区贯通判据所得的安全系数最大、比塑性区贯通率增量突变判据大 16.4%，极限平衡法所得的安全系数比塑性区贯通率增量突变判据大6.9%，总位移增量突变判据所得安全系数居中，比塑性区贯通率增量突变判据大7.8%。三维强度折减法的3种判据所得安全系数有一定的区别，主要是因为3种判据代表不同的临界状态。当整个滑带塑性区贯通时边坡可能已经处于滑动的初期，因此，在这种情况下所得安全系数最大，实际上边坡此时处于相当危险的状态；然而塑性区贯通率增量突变时滑坡基本处于临界状态，应该是处于一种更为接近真实的临界状态，因此，在这种情况下所得安全系数最小；总位移增量突变判据所得临界状态是介于前两种状态之间，因此，其安全系数也介于前二者之间。由此可以看出，根据塑性区全部贯通所得的安全系数明显偏大，采用塑性区贯通率所得的安全系数与位移增量突变所得安全系数较为接近。综上所述，总位移增量突变判据与塑性区贯通率增量突变判据在基于强度折减法的三维稳定分析中是可行的、可靠的。

由于本文是在基于滑带已知的情况下，提出了塑性区贯通率及其增量判据。如果不能获得滑带位置但知道滑坡范围时，采用位移突变判据较为实用。采用强度折减法的三维边坡稳定分析时，如果在滑带已知的情况下，由于塑性区贯通率增量突变的物理意义明确，也不需要事先选择位移特征点，建议使用塑性区贯通率增量突变作为边坡临界条件的判断依据。这两种判据应根据具体情况有选择地使用。

表4 极限平衡法与强度折减法计算的安全系数对比Table 4 Comparison of safety factors between limit equilibrium method and strength reduction method

7 结 论

（1）基于强度折减法的三维边坡稳定分析时，位移突变判据应采用总位移增量-强度折减系数曲线。因为在该曲线上较分量位移-折减系数关系曲线和总位移-折减系数关系曲线更加易于得到突变点，且位移突变特征点应选在边坡坡顶的滑体上较为合理。

（2）采用塑性区贯通率增量和强度折减系数曲线上的突变点来判定三维边坡临界状态较塑性区贯通判据更为合理。

（3）在三维边坡稳定分析采用强度折减法时，在滑带明确的情况下建议采用塑性区贯通率增量突变判据；在滑带未知的情况下建议采用位移增量突变判据。

[1]赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座 II：有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2): 332－336.ZHAO Shang-yi,ZHENG Ying-ren,ZHANG Yu-fang.Study of slope failure criterion in strength reduction finite element method[J].Rock and Soil Mechanics,2005,26(2): 332－336.

[2]迟世春,关立军.基于强度折减的拉格朗日差分方法分析土坡稳定性[J].岩土工程学报,2004,26(1): 42－46.CHI Shi-chun,GUAN Li-jun.Slope stability analysis by Lagrangian difference method based on shear strength reduction[J].Chinese Journal of Geotechnical Engineering,2004,26(1): 42－46.

[3]张培文,陈祖煜.弹性模量和泊松比对边坡稳定安全系数的影响[J].岩土力学,2006,27(2): 299－303.ZHANG Pei-wen,CHEN Zu-yu.Influences of soil elastic modulus and Poisson’s ratio on slope stability[J].Rock and Soil Mechanics,2006,27(2): 299－303.

[4]徐卫亚,肖武.基于强度折减和重度增加的边坡破坏判据研究[J].岩土力学,2007,28(3): 505－511.XU Wei-ya,XIAO Wu.Study of slope failure criterion based on strength reduction and gravity increase method[J].Rock and Soil Mechanics,2007,28(3): 505－511.

[5]栾茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3): 1－8.LUAN Mao-tian,WU Ya-jun,NIAN Ting-kai.A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J].Journal of Disaster Prevention and Mitigation Engineering,2003,23(3): 1－8.

[6]万少石,年廷凯,蒋景彩,等.边坡稳定强度折减有限元分析中的若干问题讨论[J].岩土力学,2010,31(7):2283－2288,2316.WAN Shao-shi,NIAN Ting-kai,JIANG Jing-cai,et al.Discussion on several issues in slope stability analysis based on shear strength reduction finite element methods(SSR-FEM)[J].Rock and Soil Mechanics,2010,31(7):2283－2288,2316.

[7]李红,宫必宁,陈琰.有限元强度折减法边坡失稳判据[J].水利与建筑工程学报,2007,5(1): 79－82.LI Hong,GONG Bi-ning,CHEN Yan.Study on criteria for evaluating stability of slope with FEM based on shear strength reduction methods[J].Journal of Water Resources and Architectural Engineering,2007,5(1):79－82.

[8]林杭,曹平,李江腾,等.边坡临界失稳状态的判定标准[J].煤炭学报,2008,33(6): 643－647.LIN Hang,CAO Ping,LI Jiang-teng,et a1.Analysis of the standards for critical failure state of slope[J].Journal of China Coal Society,2008,33(6): 643－647.

[9]龙绪健,黄晓燕,张春宇,等.有限元强度折减法中的刚度退化及边坡失稳判据[J].岩土工程学报,2008,30(12): 1910－1914.LONG Xu-jian,HUANG Xiao-yan,ZHANG Chun-yu,et al.Stiffness reduction and slope failure criterion in strength reduction finite element method[J].Chinese Journal of Geotechnical Engineering,2008,30(12): 1910－1914.

[10]王俊杰,马伟,张慧萍.基于强度折减有限元的非均质土坡失稳判据分析[J].河南理工大学学报(自然科学版),2013,32(1): 89－92.WANG Jun-jie,MA Wei,ZAHNG Hui-ping.Analysis of instability criterions for inhomogeneous slope based on strength reduction finite element method[J].Journal of Henan Polytechnic University(Natural Science),2013,32(1): 89－92.

[11]刘金龙,栾茂田,赵少飞,等.关于强度折减有限元方法中边坡失稳判据的讨论[J].岩土力学,2005,26(8):1345－1348.LIU Jin-long,LUAN Mao-tian,ZHAO Shao-fei,et al.Discussion on criteria for evaluating stability of slope in elastoplastic FEM based on shear strength reduction technique[J].Rock and Soil Mechanics,2005,26(8):1345－1348.

[12]马建勋,赖志生,蔡庆娥,等.基于强度折减法的边坡稳定性三维有限元分析[J].岩石力学与工程学报,2004,23(16): 2690－2693.MA Jian-xun,LAI Zhi-sheng,CAI Qing-e,et al.3D FEM analysis of slope stability based on strength reduction method[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(16): 2690－2693.

[13]陈昌禄,邵生俊,郑万坤,等.黄土高边坡的三维动力稳定性分析——以固原九龙山边坡为例[J].岩土力学,2010,31(1): 229－232,252.CHEN Chang-lu,SHAO Sheng-jun,ZHENG Wan-kun,et al.Three dimensional dynamic stability analysis of high loess slope taking the Jiulongshan slope for example[J].Rock and Soil Mechanics,2010,31(1): 229－232,252.

[14]曹云,肖武.基于强度折减和重度增加法的三维边坡稳定性分析[J].煤田地质与勘探,2010,38(3): 46－50.CAO Yun,XIAO Wu.Application of strength reduction and gravity increase method in three dimensional slope stability analysis[J].Coal Geology &Exploration,2010,38(3): 46－50.

[15]马云峰,师刚.位移突变判据在两河口水电站庆大河左岸岩质边坡三维分析中的应用[J].水利与建筑工程学报,2009,7(1): 117－119.MA Yun-feng,SHI Gang.Application of displacement mutation criteria in three-dimensional analysis on rock slope in left bank of Qingda river[J].Journal of Water Resources and Architectural Engineering,2009,7(1):117－119.

[16]陈菲,邓建辉.岩坡稳定的三维强度折减法分析[J].岩石力学与工程学报,2006,25(12): 2546－2551.CHEN Fei,DENG Jian-hui.Three-dimensional stability analysis of rock slope with strength reduction method[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(12): 2546－2551.

[17]赵尚毅,郑颖人,刘明维,等.基于Drucker-Prager准则的边坡安全系数定义及其转换[J].岩石力学与工程学报,2006,25(增刊1): 2730－2734.ZHAO Shang-yi,ZHENG Ying-ren,LIU Ming-wei,et al.Definition and transformation of slope safety factor based on Drucker-Prager criterion[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(Supp.1): 2730－2734.