基于元胞自动机模型的人员疏散仿真系统设计
2014-05-16常君明刘继清许中元
常君明,刘继清,刘 敏,许中元,沈 整
(江汉大学 数学与计算机科学学院,湖北 武汉 430056)
0 引言
随着经济与社会的高速发展,城市化进程的提速,城市人口密度越来越高,特别是公共场所人流量大、人员密集且成分复杂,潜藏着很大的安全隐患。一旦出现火灾、地震、恐怖活动等紧急状态,如果疏散不力,极易引发群死群伤等严重后果[1]。近年来,公共场所的安全疏散问题日益突出并逐步受到重视[2]。
国际国内许多机构和大专院校都在寻找解决这一问题的方法。随着计算机技术的发展,对人员安全疏散问题的研究逐步由传统的大规模演习和调查统计转向计算机仿真分析研究[3]。笔者分析了紧急情况下人员疏散的主要影响因素,提出了应急系统人员疏散处理策略,设计了基于出口距离最近的随机元胞自动机的人员疏散模型。为了更接近现实,改进和优化了人员疏散仿真算法,较好地仿真了出口个数、出口位置、出口宽度、人员数、障碍物数、疏散速度、疏散时间等因素相互之间的关系,为建筑结构设计、最大人员饱和数设定提供了参考。
1 系统仿真模型关键因素分析
1.1 人员行走消耗
在疏散过程中,人员不停地行走,个人的体力会下降,当人的体力下降到一定程度时,认定该人员将无法疏散出去。本程序中,通过记录人员行走的步数n来确定人员的体力。人所能行走的步数上限N由人为给出(通过现实生活中人员体能的取样统计获得)。
1.2 人员冲突
冲突在人员疏散中是一个很重要的影响因素。人员在移动过程中,由于人员过于拥挤或竞争,可能会导致人员之间的相互碰撞甚至践踏,文中称之为发生冲突。当发生火灾等危急情况时,人员常常会失去正常的行为规范,当空间人员密度很大时,冲突就不可避免了。竞争行为人员属性中的体力值一项[4],每经过一次冲突就会急剧减少,如果人员的体力值减少为0,就判断为个体极端拥挤危险甚至死亡。
1.3 位置吸引力
在建立当前人员的候选目标元胞时,排除了无效或不存在的元胞,在此基础上进行概率的排序来生成候选的元胞序列,这样降低了算法的难度,提高了程序执行效率。位于坐标为(i,j)的相应位置元胞的位置吸引力计算公式为[5]
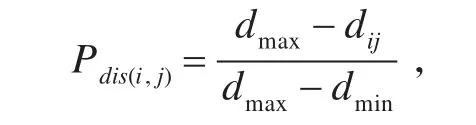
其中 Pdis(i,j)表示候选元胞中坐标为(i,j)的元胞位置吸引力概率,dmax表示候选元胞中距离出口最远的元胞与出口之间的距离,dmin表示候选元胞中距离出口最近的元胞与出口之间的距离,dij表示候选元胞中坐标为(i,j)的元胞与出口之间的距离。在候选元胞中,距离疏散出口越近的元胞,其位置吸引力概率越大,反之距离疏散出口越远,其位置吸引力概率越小。
位置与出口之间的距离算法为
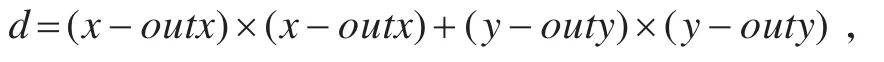
由于在程序运行中,只要判断d的大小,不需要确切知道d的具体的值,所以在计算的过程中,不对d进行开方,节省计算时间。
1.4 方向吸引力
系统采用Moore型邻域[6],元胞的可移动半径为周围的一个网格,如图1所示。紧急情况下,人员会选择最短路径走向出口,根据从自己相邻的8个网格的状态选择一个作为自己下一位置。如果人员保持原来位置不移动,表示没有当前运动方向,方向值为0。因此人员的运动方向可取值为0~8范围内的9个值。同时,人员紧急情况下对建筑物空间的熟悉程度与盲从的矛盾心理也必须充分考虑[7]。人员在进行下一步疏散行为前都有一个当前的运动方向取值。当前运动方向取值是根据前一个时间步长人员移动产生的方向趋势而确定的[5]。假设人员在t时刻的位置为Lt=(it,jt),则在t+1时刻元胞状态是由时刻t元胞及相邻元胞的状态决定的,人员移动单元格(i,j)的概率为[8]
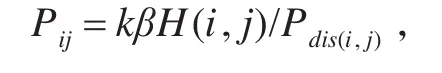
其中k为归一化系数,使相邻8个单元格的概率Pij之和为1,即ΣPij=1;β为人对建筑物空间信息的熟悉度;H(i,j)为网格状态。

图1 人员可选运动方向值Fig.1 Direction value of personnel optional movement
1.5 冲突避让规则
如图2所示的多个人员(状态值为1)同时竞争同一个空位网格(状态值为0)时的4种情况,随机选取一个元胞进入该空位网格,其他元胞则退回原地。被随机数“遣回”原地的元胞需要判断是否有机会进入其他空位网格,也就是说令该元胞重新选择路线行走,直到所有占位状态值为1的元胞都找到自己唯一的下一时刻的目标网格。此时,完成了元胞状态的第一次更新,保存数据重复以上步骤就可得到人员疏散全过程的网格占位情况[9-10]。

图2 多个人员竞争同一个目标的4种情形Fig.2 Four situations for multiple persons competing for the same target
1.6 建筑物结构排斥力
在人员疏散过程中,人员总是有意识无意识地与建筑物墙壁或障碍物保持一定的距离。疏散系统中需要考虑排斥力的作用,可用行走概率来体现这种作用力。
2 系统程序设计
2.1 疏散算法实现
笔者设计了基于出口距离最近的随机元胞自动机的人员疏散模型。为了更接近现实,改进和优化了人员疏散仿真算法,除考虑到人员疏散中常用的位置吸引力、方向吸引力、绕行规则、冲突避让规则、环境熟悉程度等因素外,还充分考虑疏散过程中人员冲突造成的相互影响,提出人群系统结构的突变情况以及对人员移动权因子分析。人机交互设计有出口个数、出口位置、出口宽度、人员数、障碍物数等。算法流程如图3所示。
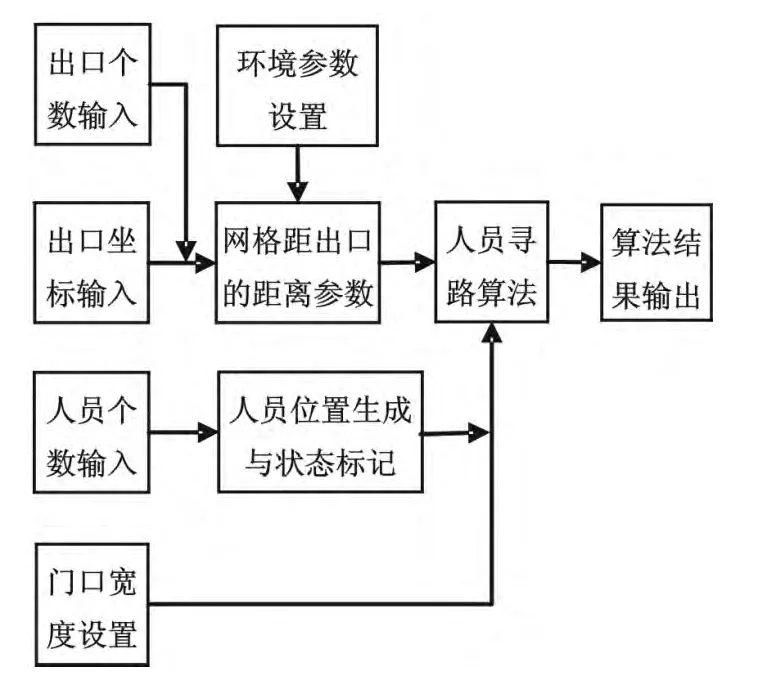
图3 疏散算法流程图Fig.3 Flowchat of evacuation algorithm
2.2 系统建模
元胞空间的研究目前集中在一维和二维空间;二维元胞自动机通常有Von.Neumann型、Moore型及Moore扩展型3个经典模型。在本程序中釆用的是Moore型。对建筑物平面空间进行均匀的网格划分,每个网格对应一个元胞。根据密集人流中典型的人员空间分配标准,每个元胞应当对应0.5 m×0.5 m的空间。则确定任一元胞A(i,j)的中心坐标 (x,y)为

基于所有人员的位置都是同步变更的模拟规则,规定每个时间步长里每个人员只能移动一个网格。那么,根据正常情况下人的行走速度是0.5 m/s的标准,以及每个元胞对应的空间是0.5 m×0.5 m的前提条件,每个时间步长耗时就应当是0.5 m/(0.5 m·s-1)=1 s。
3 系统仿真实验结果分析
系统设计有良好的人机交互界面,可以进行出口个数与位置的设置、网格属性的设置、建筑物结构设计、人员个数设置、人员随机分布等。可视化了人员疏散的动态过程、机构显示、突变点显示,效果如图4所示。
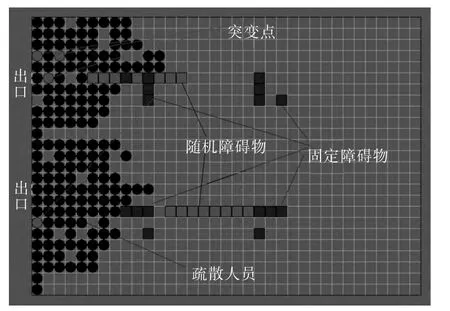
图4 系统可视化仿真过程Fig.4 Visual simulation process of system
由表1数据分析可知,当人数和障碍物一定,出口数增加时,首先会影响疏散时间,使得疏散时间变短;当出口为4个时,疏散时间减少到1个出口疏散时间的40%。其次,随着出口数增多,突变点数会急剧下降。当出口数为1时,会有大量的突变点产生,这代表出口数很少时会有大量的拥挤现象,造成人员受伤。而出口数为4时,突变点锐减至0,说明增加出口数,不仅可以缩短疏散时间,更可以减少人员受伤。
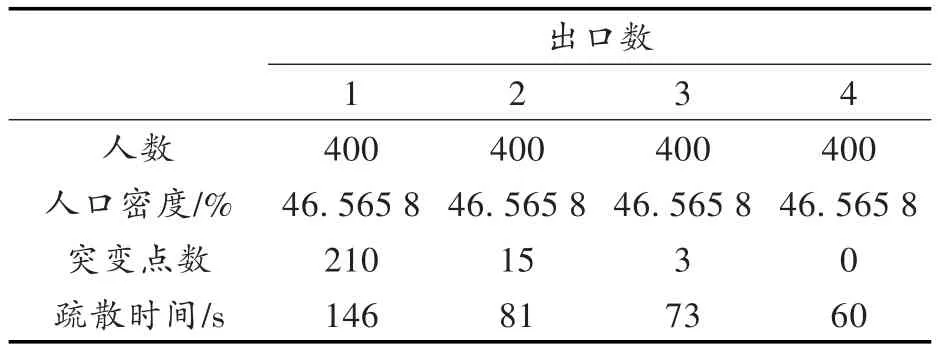
表1 人数相同、出口数不同的疏散时间和突变点统计Tab.1 Statistics of evacuation time and abrupt points with certain persons and uncertain exits
由表2数据分析可知,当出口数和障碍物一定,建筑物中容纳的人数增多时,疏散时间变大。更关键的是突变点正在急剧变大,这意味着建筑物中容纳的人员过多时,就会发生严重拥挤。因此,为了保证紧急情况下人员安全疏散,就必须限制建筑物的人数。在表2数据环境下,系统的饱和人数为350~400人。
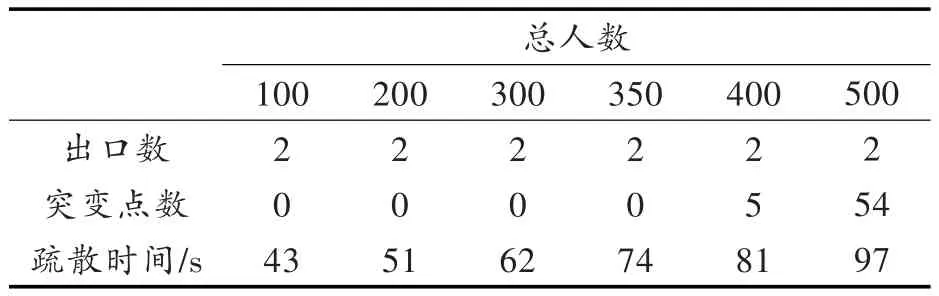
表2 出口数相同、总人数不同的疏散时间和突变点统计Tab.2 Statistics of evacuation time and abrupt points with certain exits and uncertain persons
4 结语
在Visual C++软件环境下编写了疏散过程的系统程序,设计有出口个数、出口位置、出口宽度、人员数、障碍物数等参数的良好人机界面。实验表明,系统有效仿真了出口数、人口密度、障碍物密度、突变点等参数对人员疏散效率的影响。仿真结果对设置饱和安全人数、建筑物结构设计、临时搭建提供了参考。
(References)
[1]陶平,张小英.中庭式建筑紧急情况下人员安全疏散性能研究[J].中国安全科学学报,2009,19(6):41-46.
[2]肖双喜,周星火,李向阳,等.拥挤人群疏散数学模型的研究现状探讨[J].中国安全生产科学技术,2007,3(2):107-110.
[3]方正,陈大宏,张铮,等.建筑物火灾人员疏散的计算机仿真[J].计算机仿真,2001,18(2):49-52.
[4]崔喜红,李强.大型公共场所人员疏散模型研究:考虑个体特性和从众行为[J].自然灾害学报,2005,14(6):133-140.
[5]周淑秋,孟俊仙,刘真.大型建筑物人员疏散仿真系统及实现[J].计算机仿真,2009,26(6):191-194.
[6]王长缨,周明全,张思玉.基于规则学习的林火蔓延元胞自动机模型[J].福建林学院学报,2006,26(3):229-234.
[7]关超,袁文燕.基于元胞自动机的弱视条件下群体疏散的仿真研究[J].中国安全科学学报,2008,18(12):41-49.
[8]蒋桂梅.基于元胞自动机的疏散系统的设计与分析[J].现代计算机:专业版,2009(12):78-80,83.
[9]陶平,张小英,马恒亮.基于元胞自动机模型的人员疏散仿真研究[J].计算机仿真,2009,26(10):319-322.
[10]陈锦昌,詹伟杰,姜立军.基于2.5维元胞自动机的人员疏散模型[J].工程图学学报,2009(5):170-176.
