基于改进遗传算法的四旋翼无人机参数辨识

曾玉龙，赵龙,，周建华

1. 北京航空航天大学 数字导航中心，北京 100191

2. 北京航空航天大学 飞行器控制一体化技术重点实验室，北京 100191

基于改进遗传算法的四旋翼无人机参数辨识

曾玉龙1，赵龙1,2，周建华1

1. 北京航空航天大学 数字导航中心，北京 100191

2. 北京航空航天大学 飞行器控制一体化技术重点实验室，北京 100191

为克服传统遗传算法在参数辨识过程中收敛速度慢的问题，提出了一种基于改进遗传算法的四悬翼无人机参数辨识方法。该方法引入梯度算子为遗传进化提供指示性的方向，利用遗传算法的全局搜索性保证算法的全局收敛，并根据简化四旋翼无人机数学模型设计了优化函数。利用四悬翼无人机实飞数据进行了实验测试，实验结果验证了本文方法的有效性和快速收敛性。

四旋翼无人机；刚体模型；参数辨识；遗传算法；梯度算子

目前，无人机已然在灾区救援、物资运输、军事侦察等诸多领域得到了广泛的应用，无人机的控制问题也越来越受到学界的重视。四旋翼无人直升机，以其飞行的灵活机动性以及垂直起降功能在无人机研究领域占有重要位置。近年来，针对四旋翼无人机的研究成果也越来越丰富[1]。然而四旋翼无人机由于其模型的非线性以及各变量间的耦合性，导致建模和控制问题成为该领域的关键技术问题[2]。

四旋翼无人机是一个典型的欠驱动系统，其数学模型表现出非线性和各状态的高度耦合性[3-4]，因而经典的参数辨识方法，例如最小二乘法和极大似然法等，很难实现对模型参数的精确辨识[5]。遗传算法是解决非线性问题的一个比较常用的方法，可以实现问题的全局收敛[6]。然而遗传算法存在着进化方向过于随机，收敛速度慢的问题[7-8]。梯度校正法是实现辨识问题的又一方法，算法收敛速度相对比较快，然而算法对非线性问题可能会陷入局部极小，很难实现全局收敛。

为解决上述问题，本文在遗传算法中引入梯度算子，为遗传算法进化提供一个参考方向。应用梯度下降的思想实现遗传算法的快速收敛，同时利用遗传算法的交叉变异过程跳出局部极小，实现算法的全局收敛[9]。

1 四旋翼无人机模型建立

四旋翼无人机的结构见图1。无人机机体由4个旋翼驱动，其中互为对角线的2个旋翼为1组。2组旋翼旋转方向相反，在4个旋翼旋转速度大小相同时,2组旋翼产生的反扭力矩相互平衡，4个旋翼拉力平衡重力时可以实现飞行器的悬停；当同一组旋翼转速相同而组间转速不相同时，反扭力矩的不平衡可以使飞行器产生偏航力矩；而当同一组中的2个旋翼旋转速度不同时则会产生俯仰或是滚转力矩。

图1 四旋翼无人机结构

当忽略了四旋翼无人机的机械振动和弹性形变时，系统可以简化为1个六自由度的刚体，可以应用刚体动力学方程为四旋翼系统进行建模。然而在实际飞行时，飞行器的飞行状态会受到很多复杂因素的影响，例如飞行过程中风对飞行器的影响、飞行器向前飞时各旋翼的挥舞运动等等。为便于飞行器模型辨识过程的进行，假设飞行器的飞行状态为：1）四旋翼在基本无风的飞行，不考虑风的影响；2）四旋翼处于悬停或慢速飞行状态，忽略旋翼的挥舞运动。文献[4]和文献[10]研究了此种情形下的四旋翼建模问题。

四旋翼飞行器机体坐标系和惯性坐标系之间的转换矩阵为

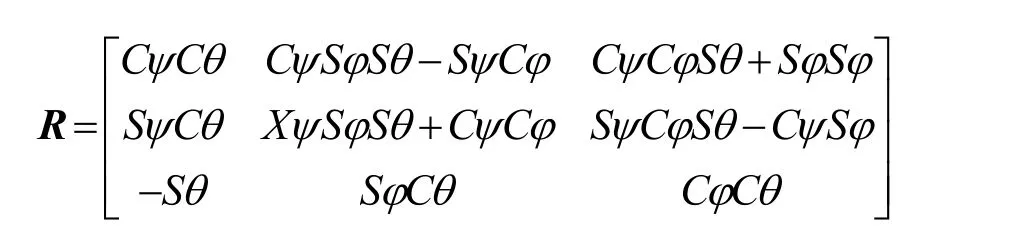
式中φ、θ和ψ分别为四旋翼的滚转角、俯仰角和航向角；符号S和C分别代表三角函数sin()和cos()。如果令η代表3个欧拉角构成的向量η=[ϕθψ]T，用ω表示机体坐标系下3个轴方向四旋翼的角速度ω=[pqr]T，则有

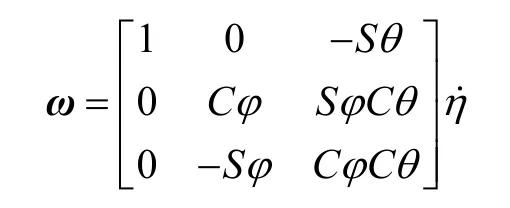
刚体运动方程可以由Newton-Euler法得到。假设四旋翼的4个旋翼产生拉力以及旋转的反扭力矩分别用下式表示

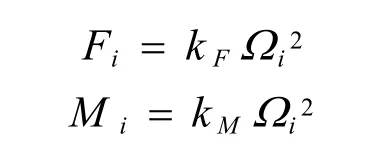
式中iΩ表示旋翼转动角速度。则刚体的平动和转动方程可以表示为

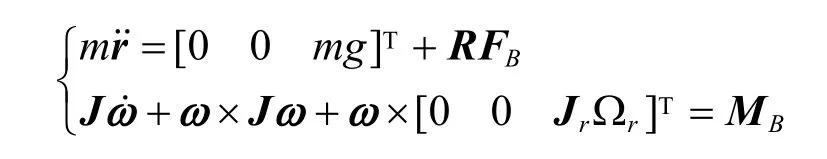
式中m表示四旋翼的质量；J表示转动惯量张量；Jr表示旋翼的转动惯量；rΩ为表征陀螺效应的相对角速度，该乘积项表征无人机4个旋翼整体的陀螺效应；FB为飞行器所受外力；MB为飞行器所受外力矩；R为坐标转换矩阵。FB和MB可表示为

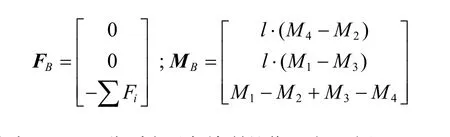
式中Fi和Mi分别表示各旋翼的作用力和力矩。

根据四旋翼结构的对称性，转动惯量张量矩阵J可以写成一个对角阵的形式。如果选取状态变量为

由于动力系统的时间常数要比电机的实现常数大得多，可以将四旋翼驱动电机的数学模型简化为如下形式[1]：

式中Vi为各旋翼电机的输入电压，K为电机常数，从而可以得到四旋翼的状态空间方程形式：

式中X为系统状态变量，其估计值可以通过惯导统得到。通过状态估计值和输入值可以实现对系统参数的辨识。

2 加入梯度算子的遗传算法

实际飞行中，四旋翼无人机数据采集主要包括输入量和输出量数据的采集，其中输出量主要由飞行器的导航系统提供。导航系统在进行数据测量过程中存在偏差，因而实际测量的状态会有一定误差，即

传统的优化函数可以表示为

为解决遗传算法收敛慢的问题，将梯度算子引入到遗传算法之中，文中近似地取优化函数为

式中N代表飞行过程中采集到的数据组数。辨识过程中利用差分近似代替微分,其表达式为式中T(k)代表飞行过程中数据的采样时间；Δt•表示差分近似的微分运算。用θ表示模型参数向量，对上式所示的优化函数取梯度可以得到新的梯度算子，即

式中：

改进遗传算法在实现时包括编码、种群初始化以及迭代进化过程3个主要部分。每一次迭代进化过程包括选择、梯度进化、交叉和变异4个主要步骤。算法流程如图2所示。

1）编码。针对四旋翼刚体模型的特点，选取1个九维双精度实向量作为染色体，采用十进制编码形式。九维向量对应刚体模型的9个待辨识定常参数{ai、k m、bj}，i=1,2,…,5，j=1、2、3。

2）种群初始化。根据选用的四旋翼无人机的类型特点以及选用电机的参数，估计各参数范围。将各参数范围综合考虑，组成1个九维矩形区域作为参数可行域。在可行域中依均匀分布随机选取若干个九维实向量作为进化算法的初始染色体组。

3）迭代进化。传统的遗传算法迭代进化过程包括选择、交叉和变异3个算子运算。为实现对遗传算法加速，文中在基本迭代运算基础上引入了梯度算子，算法过程包括选择、梯度、交叉和变异4个步骤。而且为保证算法的收敛性，算法在每代进化中保留亲代中的最优值。

a）选择算子。算法根据优化函数计算出每一代迭代运算中得到染色体组的适应度值，根据适应度值分配梯度算子和交叉算子选取亲本的概率。

b）梯度算子。根据选择算子得到的概率选择亲本，并根据梯度公式对亲本实施一步梯度计算并加入到子代染色体组中。

c）交叉算子。采用传统十进制交叉算法，选取2个亲本染色体之后对亲本进行加权融合，得到2个新染色体并加入子代染色体组中。

d）变异算子。采用传统的十进制变异算法，根据概率对选中的子代染色体加入一个随机生成的九维向量，同时保证变异后子代处于可行域内。

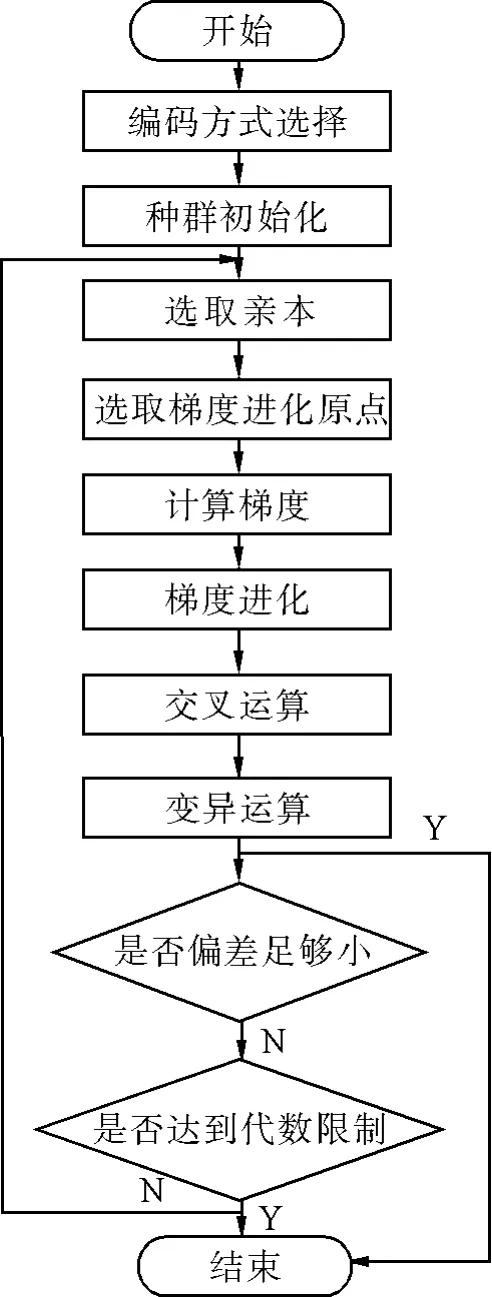
图2 改进遗传算法流程

3 仿真算例

文中利用实验四旋翼无人机的实飞数据对无人机的刚体模型参数进行辨识和验证测试。

由于待辨识参数多，且四旋翼无人机模型中姿态控制回路和位置控制回路的参数间存在一定的独立性，为简化仿真计算，将四旋翼各参数进行分组辨识。文中把待辨识参数分为俯仰回路、滚转回路、航向回路以及位置回路四个部分分别进行辨识，并取100代遗传最优值作为辨识结果。

从俯仰回路参数辨识结果中得到的俯仰回路辨识轨线与实际飞行轨线对比如图3所示。

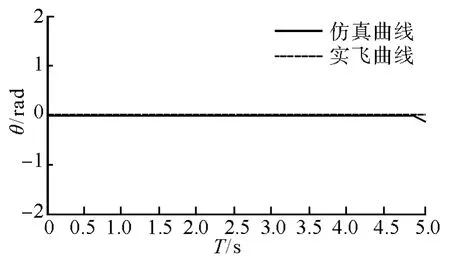
图3 俯仰回路辨识结果

从图3中可以看出，俯仰角回路的辨识结果同实际飞行结果非常接近。2组数据只是在最后一段时间出现了一定的偏差，该偏差主要是由飞行数据误差引起的。偏航角回路辨识结果对比轨线如图4所示。

图4 偏航回路辨识结果

从图4中可以看出，与俯仰回路不同，偏航回路辨识结果存在一个角度的常值误差。在辨识过程，一方面由于惯导系统的漂移会使系统出现一些误差；另一方面航向角的基准方向选取过程也存在一定误差；再者，遗传算法由于选取有限代数的进化结果作为最终辨识结果。故此，辨识结果存在一定程度的偏差。

滚转角辨识结果对比曲线如图5所示。滚转角回路的角速度辨识结果存在一个常值误差，使得角度偏差等幅增大。在本回路中，误差主要是算法的有限代结果存在的误差引起的，此外回路相关参数过小也会导致角速度辨识过程出现误差。

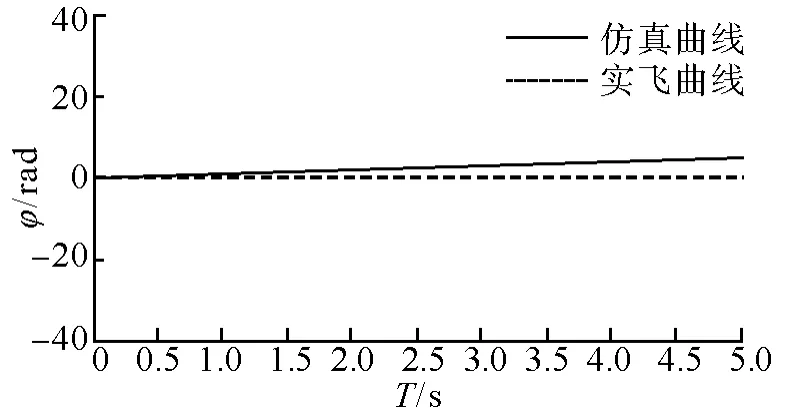
图5 滚转回路辨识结果对比

四旋翼的3个位置环对应的输入参数都只有油门输入量，3个方向具体的运动形式主要通过无人机的姿态角来具体实现。因而3个位置回路待辨识参数只有1个，即油门输入的增益值。图6为高度的辨识结果同实飞数据对比结果。

图6 高度辨识结果对比

从图6中可以看出，位置辨识结果同样存在着常值的偏差，该误差主要是由于高度测量的定位偏差引起的。此外算法的有限步取值同样也会引起辨识误差。

文中利用梯度算子对传统的遗传算法进行了改进，意在加速算法的收敛过程。为比较加入梯度算子前后辨识过程的收敛情况，在同样条件下利用传统的遗传算法对四旋翼的参数辨识问题进行了求解，分别求出了2种算法的优化函数值。改进遗传算法同传统遗传算法的收敛情况对比曲线如图7所示。

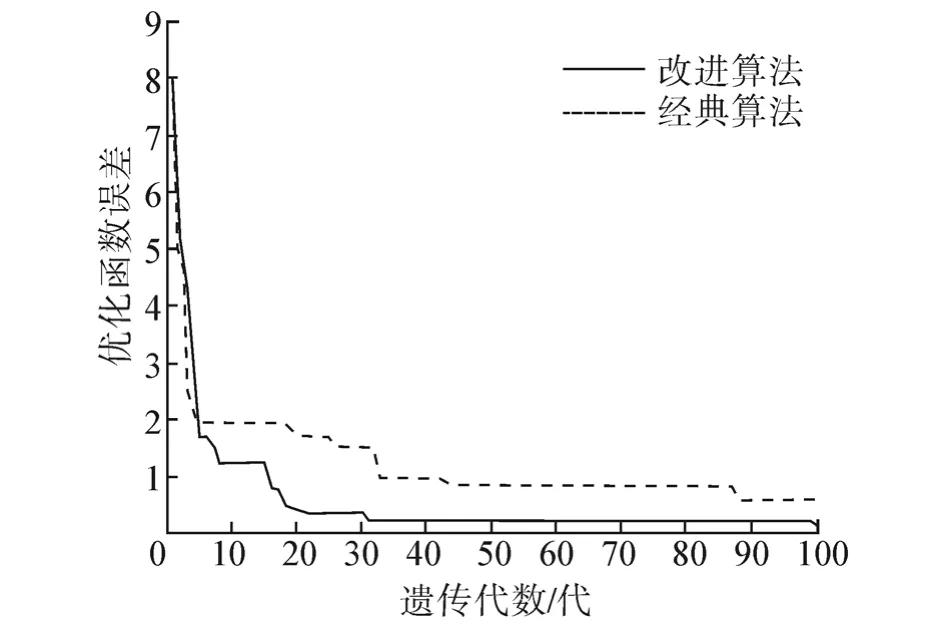
图7 改进遗传算法收敛情况对比

从图7中可以看出，在引入梯度算子后，参数误差降至初始种群5%时，进化代数由传统遗传算法的87代下降到17代。从效果上来看，改进算法收敛速度较之传统遗传算法有了一定程度的提升。

4 结束语

针对四旋翼无人机系统辨识问题，利用梯度算子对遗传算法参数辨识过程进行改进，获得了四旋翼无人机的刚体数学模型。利用实际试飞数据进行仿真测试，测试结果表明，引入梯度算子加快了遗传算法的收敛速度，增加了算法的鲁棒性。

对于文中研究的问题还需进一步完成：1）针对四旋翼模型特点对算法过程进行进一步优化，实现算法运行速度的进一步改进；2）进一步优化梯度算子的表现形式，对算法进行进一步的加速。

[1] 岳基隆. 四旋翼无人机自适应控制方法研究[D]. 长沙: 国防科学技术大学, 2010: 11-37.

[2] 吴桐, 赵健康, 杨磊. 四旋翼无人机的系统模型与辨识[J].计算机仿真, 2012, 29(8): 89-92.

[3] BOUCHOUCHA M, TADJINE M, TAYEBI A, et al. Step by step robust nonlinear PI for attitude stabilisation of a four rotor mini-aircraft[C]// 16th Mediterranean Conference on Control and Automation. Ajaccio, France, 2008: 1276-1283.

[4] WANG Tianmiao, WANG Liewu, LIANG Jianhong, et al. Autonomous control and trajectory tracking of quadrotor helicopter[J]. Computer and Modernization, 2012 (5): 251-255.

[5] 李鹏波, 胡德文, 张纪阳, 等. 系统辨识[M]. 北京: 中国水利水电出版社, 2010: 169-174.

[6] 孙增圻, 邓志东, 张再兴. 智能控制理论与技术[M]. 北京:清华大学出版社, 2011: 347-387.

[7] 金菊良, 杨晓华, 丁晶. 标准遗传算法的改进方案——加速遗传算法[J]. 系统工程理论与实践, 2001 (4): 8-13.

[8] GUO Pengfei, WANG Xuezhi, HAN Yingshi. The enhanced genetic algorithms for the optimization design[C]// 3rd International Conference on Biomedical Engineering and Informatics. Yantai, China, 2010: 2990-2994.

[9] 于志刚, 宋申民, 段广仁. 遗传算法的机理与收敛性研究[J].控制与决策, 2005, 20(9): 971-980.

[10] NAGATY A, SAEEDI S, THIBAULT C, et al. Control and navigation framewoek for quadrotor helicopters[J]. J Intel Robot Syst, 2013 (5): 251-255.

Parameter identification for quadrotor UAVs based on an improved genetic algorithm

ZENG Yulong1, ZHAO Long1,2, ZHOU Jianhua1

1. Digital Navigation Center, Beihang University, Beijing 100191, China
2. Science and Technology on Aircraft Control Laboratory, Beihang University, Beijing 100191, China

In order to work out the low convergence speed problem in the process of parameter identification in which the genetic algorithm is adopted as the main section, a new method of parameter identification process is developed for the quadrotor UAV model, which is constructed based on an improved method of the GA process. This method introduced a gradient operator into the GA process to offer a sort of direction for algorithm evolution. The global convergence of the algorithm is guaranteed by the global search property of the GA and an optimal function is designed with the simplified quadrotor model. A test with the data gained from the actual flight experiment of the quadrotor is made and results proved the effectiveness and rapid convergence property of this method.

quadrotor UAV; rigid body model; parameter identification; genetic algorithm; gradient operator

N945.14; TP23

A

1009-671X（2014）01-0001-05

10.3969/j.issn.1009-671X.20130620

2013-06-18.

国家自然科学基金资助重点项目(61039003)；国家自然科学基金资助项目（41274038）；中国航空基础科学基金资助项目(20100851018)；中国航天创新基金资助项目（CASC201102）.

曾玉龙（1988-），男，硕士研究生；赵龙（1976-）, 男，副教授，博士.

赵龙, E-mail: flylong@buaa.edu.cn.