填料密封阻塞下气体螺旋密封的数值模拟研究
2014-05-14潘华辰祝佳乐
潘华辰,祝佳乐
(杭州电子科技大学机械工程学院,浙江杭州 310018)
0 引 言
流体密封技术是保证机械设备正常运转、衡量机械设备可靠性的重要手段。因此,研究流体密封机理,探索新的实用型流体密封技术,提高机器设备密封的可靠性,不仅具有重要的理论和实际意义,还有重要的经济价值。
螺旋密封是一种非接触型流体动密封,它是近几十年发展起来的一种新型转轴密封结构。由于螺旋结构和轴套之间存在间隙,两者之间永远不会发生摩擦接触,可以在较高转速下使用且工作寿命很长[1]。但是在气体条件下,因气体粘度小,密封效果差。此外,考虑停车时的密封,气体螺旋密封往往还需要用填料密封进一步保证有效密封。在正常运行时,填料密封还在起作用,所以实际气体螺旋密封的问题是螺旋密封本身泄漏和填料密封泄漏问题的相加。在传统的螺旋密封理论文献和进一步的研究中[2-7]往往忽略了填料密封及其泄漏的因素,所以与实际情况有一定差距。
多孔介质概念用于研究填料密封问题时,主要参数是渗透率,其定义为单位压力梯度,单位动力粘度系数下的流体在介质中的渗透速度。渗透率是多孔介质本身的属性,需通过试验测定。本研究利用多孔介质概念来类比填料密封泄漏的机理,建立相应的计算模型,对填料密封和螺旋密封共同作用下的气体密封问题进行数值模拟。
1 螺旋密封结构
螺旋密封是一种利用流体动压反输的径向非接触型转轴密封。典型的螺旋密封结构[8]如图1所示。
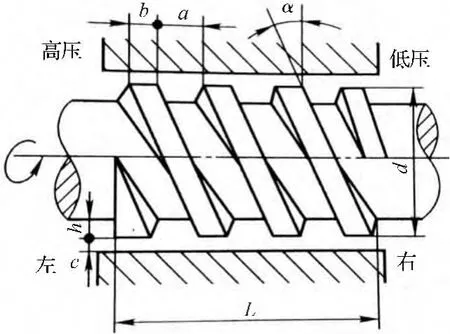
图1 螺旋密封结构
本研究采用气体密封,为获得满意的密封效果,在图1的右端添加填料密封,使填料填满整个腔体。本研究所采用的添加填料密封的具体结构如图2所示。
添加填料腔体具体结构尺寸如下:
螺旋总长L=100 mm,螺旋外径d=120.5 mm,槽深 h=0.375 mm,螺旋角 α =2.5°,槽宽 a=2 mm,头数i=4,齿宽 b=2 mm,间隙 c=0.025 mm。
填充填料的腔体:内径 D1=95 mm,外径 D2=121 mm,长度l=50 mm。
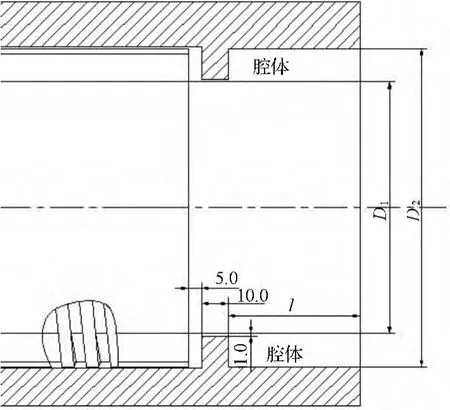
图2 腔体结构(单位:mm)
2 网格处理
本研究用Gridgen建立计算网格。螺旋结构的网格较难处理,尤其在螺旋线的两个端点上,因为相切最后边界会形成一个角,若采用六面体网格来划分的话,相邻网格的角度大,正交性差,且大大增加了网格数量,这样处理的网格质量不高,计算时间长,收敛慢,且会降低计算精度。若全部采用非结构网格来处理,虽然网格生成简单了,但计算量大、计算稳定性不够,收敛慢,计算结果可能有偏差。因此,本研究采用混合网格来处理,边界角处采用如图3所示的非结构网格来划分,而其他地方采用结构网格来处理。这样降低了网格划分的难度,减少了网格数量,缩短了计算时间,加快了收敛速度,也满足了计算精度的要求。放置填料的腔体,结构规整,适合生成六面体网格。

图3 非结构网格
因为间隙小,若间隙内网格层数少,难以真实反映边界层内的情况;若层数多,则会增加网格数量,所需计算资源大大增加。经过反复试验,间隙内5个控制点比较合适,因为间隙比较小,采用平均分布。一条螺旋线上的网格生成如图4所示,最终全部网格数量为265 088个,通过Gridgen网格检查,没有负网格的产生,网格质量较高。

图4 一条螺旋线上的网格
3 计 算
螺旋密封及填料密封介质是气体,因此它的控制方程是纳维-斯托克斯(N-S)方程。N-S通用表达式[9]如下:
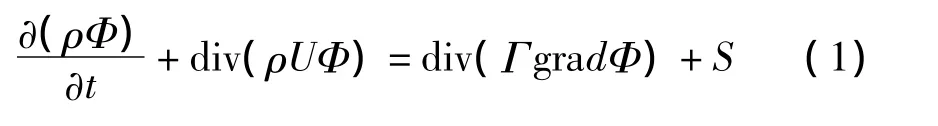
式中:ρ—流体密度;t—作用时间;第一项—瞬态相;第二项—对流相;第三项—扩散相;最后一项—源项;Φ—通用变量,包括速度分量u、v、w、温度T等变量;Г—广义扩散系数;S—广义源项。
具体到各个方程,通用式中各个符号意义如表1所示。

表1 符号具体形式
湍流模型SST(Shear Stress Transport)基于k-ω方程发展而来,该方程考虑了湍流剪切力的传输,综合了k-ω模型在近壁区计算的优点和k-ε模型在远场计算的优点,可以准确预测流体的分离特性,特别适合高精度边界层的模拟。本研究中螺旋结构与壁面之间的间隙比较小,对近壁面内的模拟要求高,所以采用SST模型来计算。SST的k方程和原始的k-ω方程中的k方程一样,而ω方程如下[10-11]:
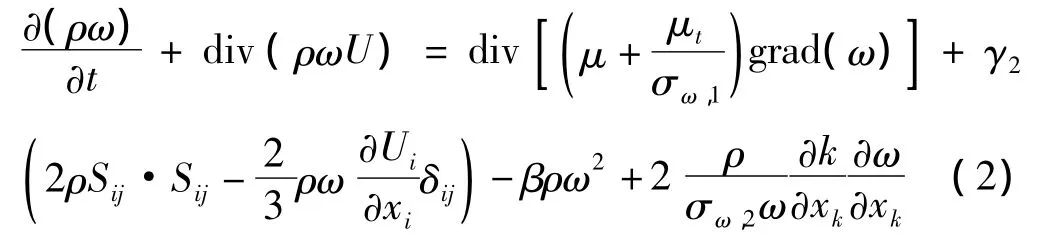
其中,默认常数一般设为:σω,1=2.0,σω,2=1/0.856,β =0.083。
多孔介质渗透率计算公式[12]为:

式中:μ—动力粘度,l—渗透距离,ΔP—压力降,v—渗透速度。
多孔介质条件下对流—扩散方程变为:

式中:γ—孔隙率,K—面积孔隙率张量。
流体一般的动量方程为:
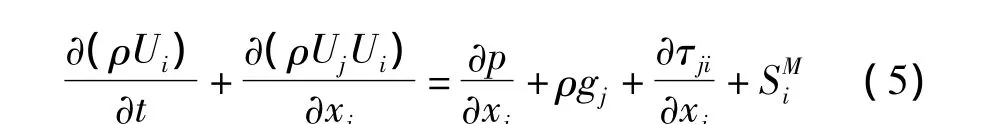

式中:CR1—线性阻力系数,CR2—二次阻力系数,—包含其他动量源项,U—表观速度。
多孔介质达西定律通用表达式为:
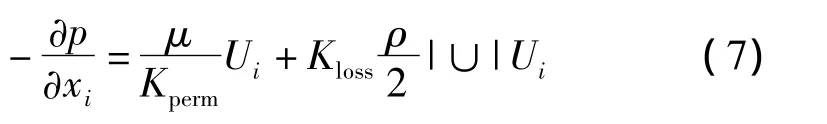
式中:μ—动力粘度,Kperm—渗透率,Kloss—经验损失系数。
比较式(6)和式(7),得:
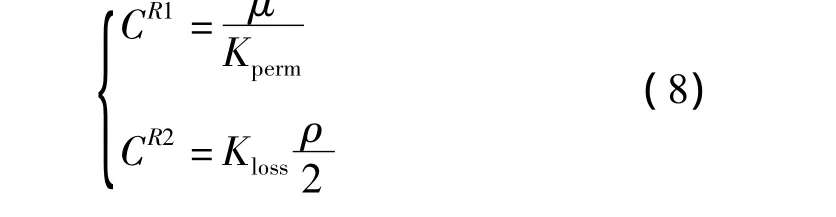
以上就是多孔介质模型计算的基础。本研究的数值计算使用CFD的通用软件“CFX13.0”,采用稳态模拟。在差分格式中,笔者选用高阶求解(High Resolution),模拟的介质选用25℃空气,暂不考虑热量传输。在边界条件设置中,螺纹与壁面间隙设置为旋转域,转速为1 450 rev/min,两端压差50 000 Pa,多孔介质区域只考虑同向性,壁面采用无滑移壁面。
4 计算结果分析
本研究对图1、图2所示参数的螺旋密封算例进行数值计算时,设定设计泄漏量为进口流量的1%,通过对填料密封的渗透率经过不断的调整,得到填料密封渗透率Kperm=7.4×10-13m2。填料内部的压力分布图如图5所示,螺旋结构和壁面之间的压力分布图如图6所示,局部间隙的速度矢量图和出口处的速度矢量图如图7、图8所示。
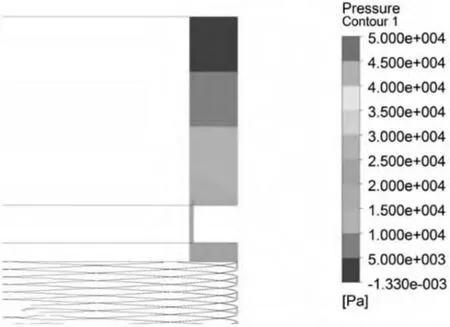
图5 压力分布图
图6 局部压力分布图
从图5、图6中可以明显看出,经过螺旋密封和填料密封,压力迅速降低,达到降压的目的。

图7 间隙处速度矢量图
图8 出口处速度矢量图
从图7、图8中可以看出,出口处的速度几乎为0,泄漏量微乎其微,起到了明显的密封作用,验证了填料密封配合螺旋密封良好的密封效果。
螺旋角α、间隙c、槽深h等对螺旋密封都有影响。笔者在上述工况条件下,设定泄漏量为进口流量的1%不变,分别对角度α和槽深间隙比n对填料密封渗透率的具体取值进行了计算。槽深间隙比n的定义为n=h/c。间隙c=0.025 mm时,相对应的角度α和槽深间隙比n在上述条件下对填料密封渗透率的具体取值如表2所示。
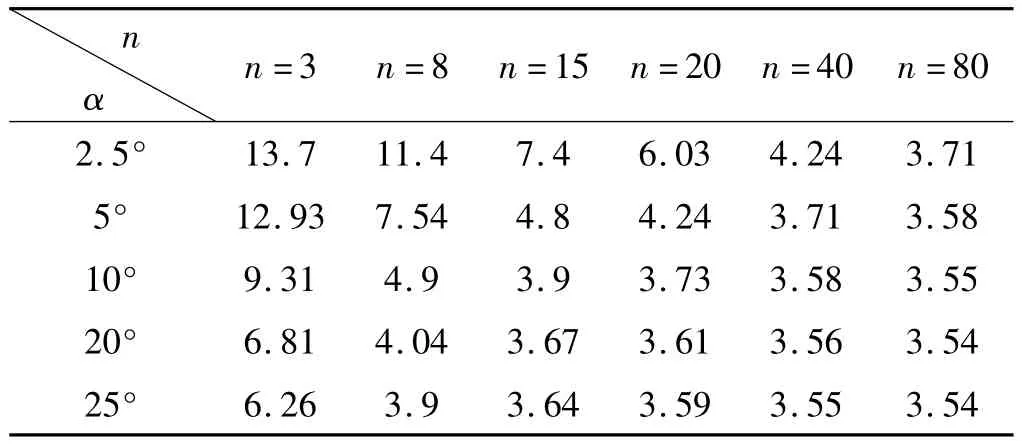
表2 填料密封渗透率
表2数据说明,在不同的结构下,螺旋密封和填料密封在整个密封过程中起到的重要程度不同。渗透率大说明对填料密封的要求低,螺旋密封起主要作用;渗透率小说明对填料密封要求高,这时填料密封起主要密封作用。比如当螺旋角为2.5°,槽深间隙比为3时,渗透率为13.7×10-13m2,这时渗透率比较大,螺旋密封起主要作用,填料密封起辅助作用。本研究对表2的取值进行了二次拟合,得到的渗透率和角度、槽深间隙比的关系如图9所示。

图9 渗透率和角度、槽深间隙比的关系
从表2、图9中可以看出,在一定压力下,填料密封的渗透率随槽深间隙比n的增大而减小,且随着n的变大,渗透率变化越来越小,当n超过一定的值时,渗透率基本没有变化,成明显的反比例关系,说明槽深的增加会使泄漏量增加,降低了可密封压力,从而需要更小的渗透率,当超过一定的n时,螺旋密封作用降低,填料密封起主要作用。从表2、图9中也可以看出,在槽深间隙比一定的情况下,随着角度的慢慢变大渗透率逐渐减小,当角度大到一定程度时,出现了类似槽深一样的情况,成反比例关系。如n=80,随着角度的变化,渗透率变化很小。
当槽深h=2 mm,角度 α=2.5°时,间隙 c对填料密封渗透率的影响如表3所示。对表3的取值,进行拟合后,得到的渗透率和间隙的关系如图10所示。
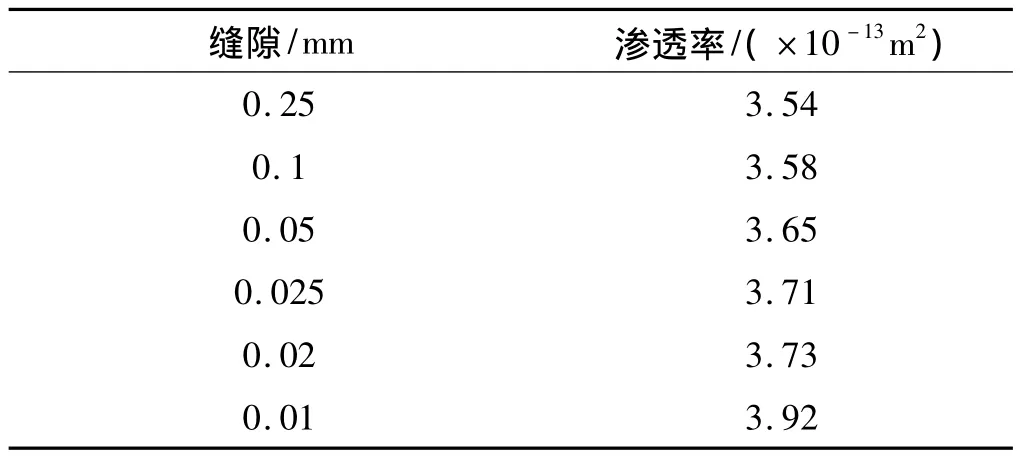
表3 渗透率取值
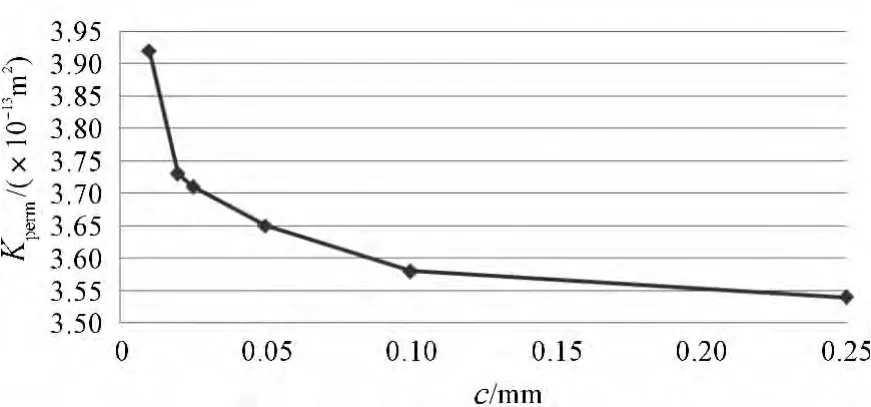
图10 渗透率和间隙的关系
从图10、表3中可以看出,间隙对填料密封的渗透率有着显著的影响。间隙减小,渗透率就随之增加。说明间隙的减小可以减小泄漏量,间隙越小泄漏量就越小,渗透率就可以随之变大,而不影响密封效果。
5 结束语
(1)本研究为填料密封作用下的螺旋密封设计提出了一种新型的密封分析方法,为填料密封作用下的螺旋密封设计提供了一定的理论基础。
(2)在给定密封泄漏率条件下,填料密封渗透率和螺旋结构存在紧密的联系,渗透率分别随着角度、间隙及间隙槽深比的增大而减小,成反比例关系。当角度、间隙及间隙槽深比增大到一定范围时,螺旋密封效果大大降低,这时填料密封在整个密封装置中起主要的密封作用。
(3)研究结果表明,填料密封配合螺旋密封,在一定的密封要求下,即使密封介质是气体也可以保证良好的密封性能。
[1] 李爱学,王者文,施 勇.螺旋密封的设计及在流体机械中的应用[J].通用机械,2010(8):72-76.
[2] HOFSETH O.Liquid seal pump with helical screw[J].Sealing Technology,2003(2):11-12.
[3] BOON E F.Hydrodynamic seal for rotating shafts[J].Chemie lngenieur-Technik,1959,31(3):202-212.
[4] 刘 杰.高压工况下车氏螺旋密封几何结构优化设计[J].机械制造,2012(7):61-63.
[5] 杨绮云,高靖宇.食品超高压设备金属密封圈失效机理及有限元[J].包装与食品机械,2013(3):34-37.
[6] 刘 杰,李 鲲,吴兆山,等.镶嵌式直线深槽流体动压型机械密封性能研究[J].流体机械,2013,41(12):16-21,26.
[7] 牛 犇,张 杰,焦 让.水润滑轴承螺旋密封性能的仿真分析[J].润滑与密封,2009(4):80-83.
[8]黄志坚.现代密封技术应用[M].北京:机械工业出版社,2008.
[9] 王福军.计算流体动力学分析 CFD软件原理与应用[M].北京:清华大学出版社,2004.
[10]刘 涵.离心泵的数值模拟及性能分析[D].杭州:杭州电子科技大学机械工程学院,2013:33-34.
[11] 丁 佳.γ型槽与螺旋槽干式气体密封性能对比研究[J].轻工机械,2012,30(3):103-105.
[12]仵彦卿.多孔介质渗流与污染物迁移数学模型[M].北京:科学出版社,2012.
