基于瞬态Ar方程的非线性涡流无损评价数值模拟

，

（1.中国工程物理研究院 总体工程研究所，绵阳 621900；2.西安交通大学 航天航空学院，西安 710049）

碳素钢等磁性材料因其良好的力学性能和耐腐蚀性被用作核电站中主要的结构材料。地震等强载荷产生的塑性变形等机械损伤可能导致结构材料断裂和失效，结构材料塑性变形等机械损伤的定量无损检测和评价是保证核电站安全的关键技术。

国内塑性变形损伤传统评价方法主要有基于金相分析、硬度压痕测试和X射线衍射法等，属于破坏性测试或无法在现场使用。国内外基于非线性涡流检测的试验研究如日本M.SHI WA基于非线性涡流信号，研究发现非线性涡流信号频谱分析后的三次谐波分量幅值随铬钼钢焊后热处理温度发生显著变化［1]。日本东北大学 T.TAKAGI和 T.UCHIMOTO研究过非线性涡流信号与石墨铸铁中白口组织（铸件内部因含渗碳体导致局部过硬的缺陷）含量以及铸铁内石墨形态特征的相关性［2－3]。

笔者之前就非线性涡流检测对碳素钢材料的塑性损伤评价开展了一些试验研究，而国内外关于非线性涡流检测的数值模拟还未见研究报道。作为非线性涡流数值模拟的一个尝试，基于Ar方程和Crank－Nicholson直接积分法首次开发了非线性涡流数值模拟程序，并且通过对比数值模拟结果与试验检测结果，证明了塑性变形导致的磁导率变化是非线性涡流检测信号变化的直接诱因，也验证了非线性涡流检测对碳素钢等磁性材料塑性变形无损定量评价的可行性。

1 瞬态Ar方程

磁准静态场（MQS）的麦克斯韦方程忽略位移电流密度项，其微分形式的基本方程组为［4]：

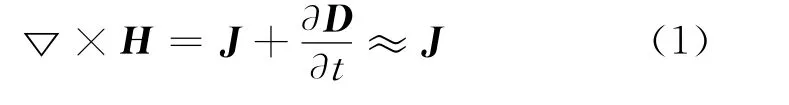
式中：H为磁场强度，A·m－1；J为电流面密度，A·m－2；E为电场强度，V·m－1；B为磁感应强度，T；D为电通密 度，C·m－2；ρ为电 荷 体 密 度，C·m－3。

由于磁场B是无源场，所以有▽·B＝0，引入一个矢量函数A（称为磁矢位）使得B＝▽×A，推导可得：

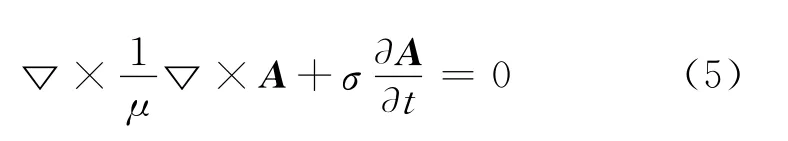
对全体分析区域进行划分，并定义各个划分区域（如图1）：

全体区域：衰减区域＋混合区域＋正常区域。

衰减区域：仅由变形矢量磁位Ar记述的区域Vr。

混合区域：Ar和仅依赖电流源的As相混合的一层有限元区域Vtr。

正常区域：由通常矢量磁位A（＝Ar＋As）记述的区域Vt。

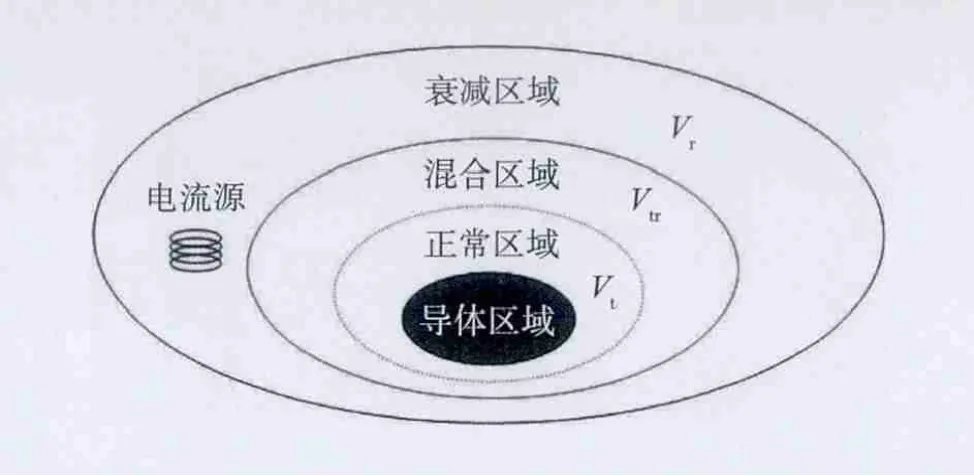
图1 分析区域划分示意图

导体区域：包含在正常区域中的导体区域。

其中总磁矢位A＝Ar＋As，Ar称为变形磁矢位，As是仅仅由电流源所产生的磁矢位。由于在分析区域内仅依赖电流源的场As和仅依赖涡电流源的场Ar是独立考虑的，所以不划分电流源的网格。

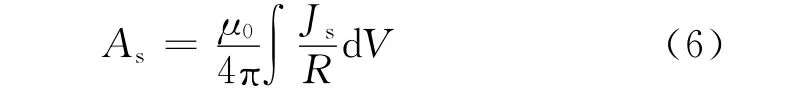
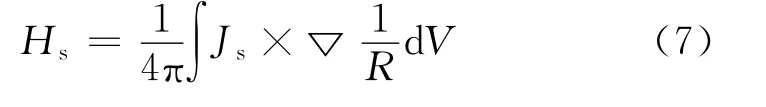
由式（1）和（5）可得在空气中：

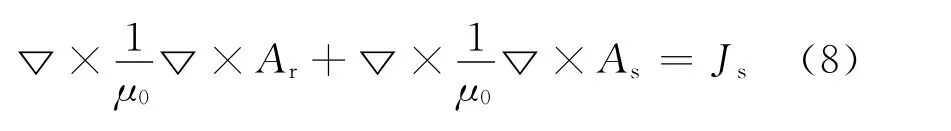
所以低频涡流场微分控制方程为：

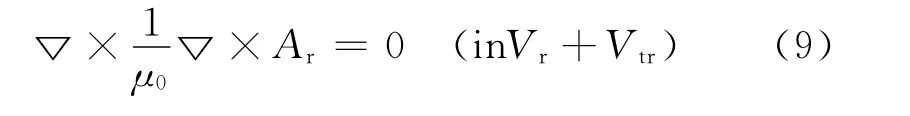
由式（5）可得在导体中：

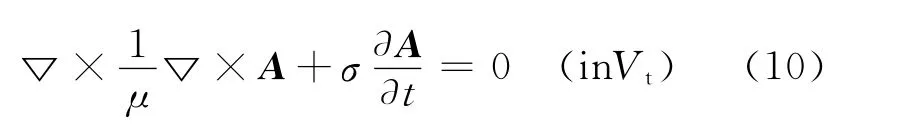
由磁场的连续性边界条件得：

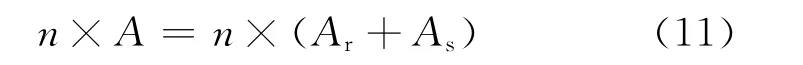
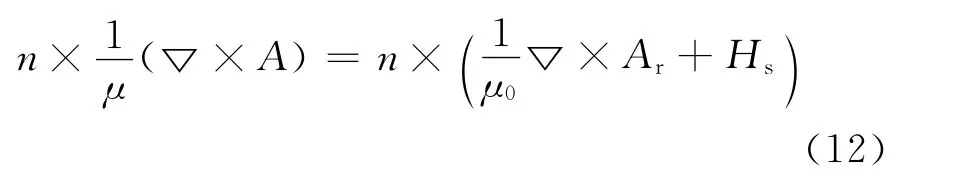
利用六面体棱边元方法对微分控制方程式（9）～（12）进行有限元离散可得伽辽金有限元方程如式（13）：

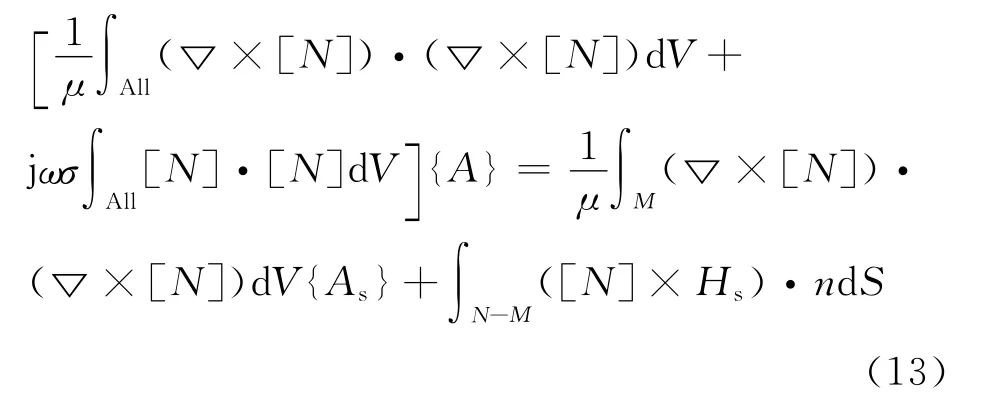
式中：［N]为矢量形状函数；n为单位法线矢量。

可简写为：

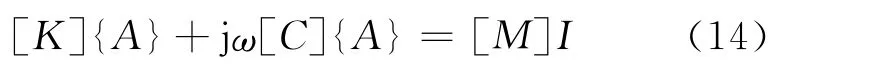
2 数值模拟程序改良与开发

将非线性涡流数值模拟作为瞬态问题而非复数问题处理，基于变形磁矢位低频涡流场控制方程式（14）可写成：

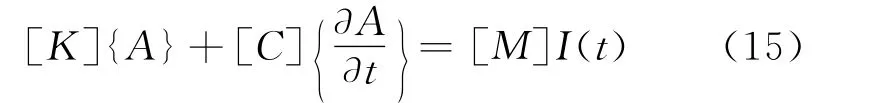
式中：［K]，［C]，［M]为全局系数矩阵；I（t）为依赖于时间函数的激励电流，采用正弦激励电流；A为矢量磁位，Wb·m－1。

对于瞬态问题，矢量磁位A关于时间的导数∂A/∂t可由关于时间步的差分（Ak－Ak－1）/Δt近似计算，其中Ak＝A（t0＋kt），k表示第k次时间步，t表示时间步长，t0表示初始时间。为了提高计算稳定性，矢量磁位A可由Crank－Nicholson直接积分法替换：

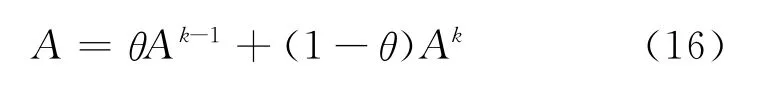
式中：0≤θ≤1为控制积分稳定性的参数。

将式（16）代入式（15），则当前步的矢量磁位A可通过式（17）计算出来。

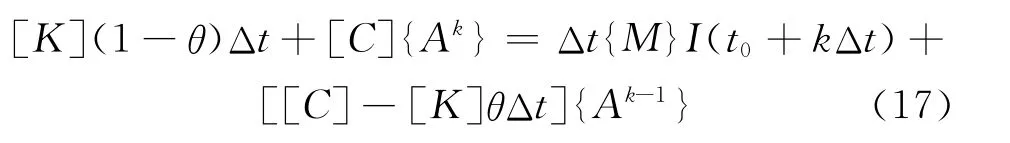
对于常规涡流法的数值模拟通常将材料的磁导率视为一定值来处理。因控制方程的刚度矩阵与单元的磁导率相关，将所有导体单元的磁导率定义为一个数组，以每个单元中心的磁感应强度作为判定参数，满足一定条件则对该单元的磁导率进行重新赋值，然后进入下一个积分时间步。直至所有积分时间步计算完成，输出所有时间步检测线圈的电压检测值。

利用定长时间步的Crank－Nicholson直接积分法改良低频涡流场的数值模拟程序，在逐步积分法的每个时间步中导入碳素钢相对磁导率μr和磁感应强度B的非线性磁化曲线，通过非线性磁化曲线对磁导率进行重新赋值，而不同于常规涡流法中将磁导率视为一个定值来处理。图2所示为所采用的碳素钢μr－B近似磁化关系曲线［5]。

将μr－B关系曲线近似分为若干个区间，通过式（17）计算出矢量磁位A，从而可以计算出磁感应强度B。如果某一积分时间步计算所得的单元中心磁感应强度B满足Bi＜B＜Bi＋1，则通过式（18）的迭代方法对该单元磁导率重新赋值：

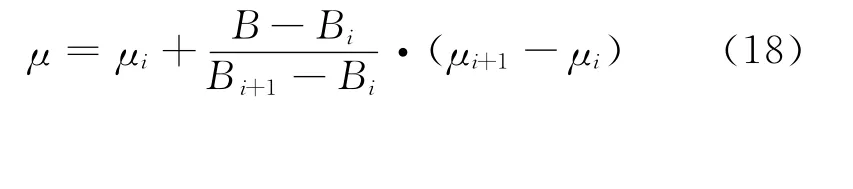
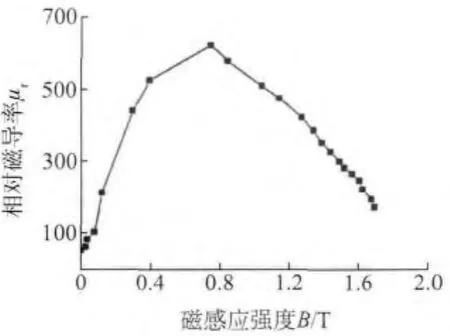
图2 碳素钢μr－B关系曲线

重新赋值后的磁导率进行单元刚度阵组装并进行下一次的积分时间步的信号计算。最后输出所有时间步的检测信号。由此，基于瞬态Ar方程并改良后的模拟程序可计算得出非线性涡流模拟信号。

3 模型算例与结果

利用定长时间步的Crank－Nicholson直接积分法改良开发的数值模拟程序，在逐步积分法的时间步中导入碳素钢的非线性磁化曲线，可获取非线性涡流的数值模拟信号。图3所示为非线性涡流法的数值计算模型，为了提高计算速度，采用有限元和棱边元方法对整个分析区域进行离散，将导体外电流源的作用等效在导体的边界上，因此线圈是不需要网格划分的，只需要对导体区域和空气区域进行网格划分。在计算模型中激励线圈和检出线圈直径15 mm，高3 mm，匝数500。

图3 非线性涡流数值计算模型

根据导入的非线性磁化曲线，采用开发的非线性涡流数值模拟程序计算得到，在任意激励频率下的非线性涡流检测信号。在激励线圈中施加一正弦电流，图4为检出线圈中得到的检测信号与正弦激励信号对比图，从图中可见检测信号不完全是一正弦信号，出现了倍频信号。

碳素钢发生塑性变形后会产生反磁致伸缩效应，材料内部微观组织发生贝氏体等相变导致磁各向异性，从而影响材料的初始磁导率等电磁特性［6－9]。根据该原理，在非线性涡流检测信号的数值模拟中通过改变图2中材料的初始磁导率（假定范围为60～85 H/m），等效模拟材料不同程度塑性变形的情况。对所得到的检测信号进行傅里叶变换的频谱分析之后得到信号的功率频谱图如图5所示，图中可见基波和高次谐波的波峰。

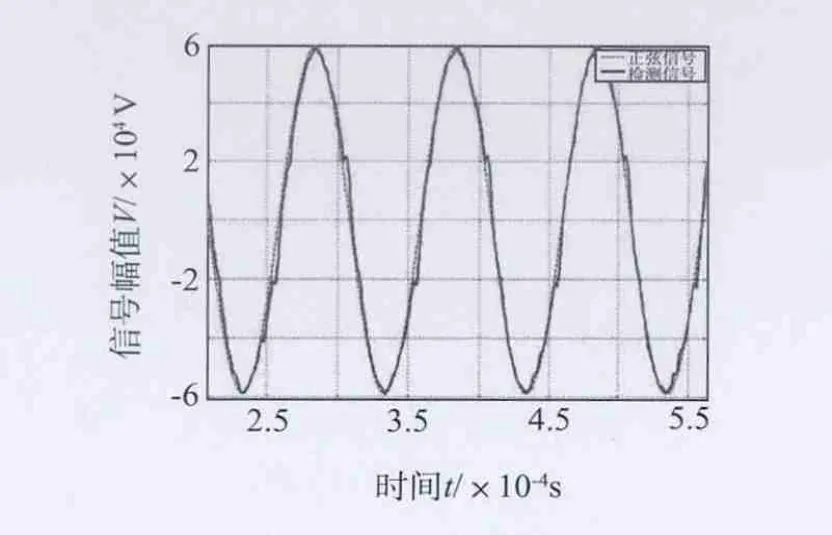
图4 非线性涡流数值模拟信号

在数值模拟中任意选取10 kHz作为激励频率，计算得到不同初始磁导率情况（即不同程度塑性变形）下材料的非线性涡流信号，提取检测信号频谱图中基波、三次谐波对应的幅值参数，可得到不同初始磁导率情况（即不同程度塑性变形）下的关系结果，如图6所示。

由以上关系结果图可发现非线性涡流模拟信号频谱图中基波幅值、三次谐波随材料的初始磁导率即塑性变形程度的增大出现下降的趋势，这一趋势与此前试验中碳素钢的检测结果是一致的。

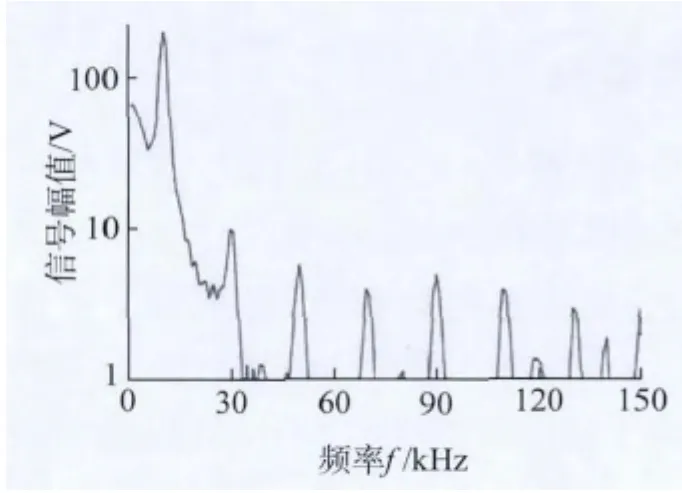
图5 非线性涡流模拟信号频谱图

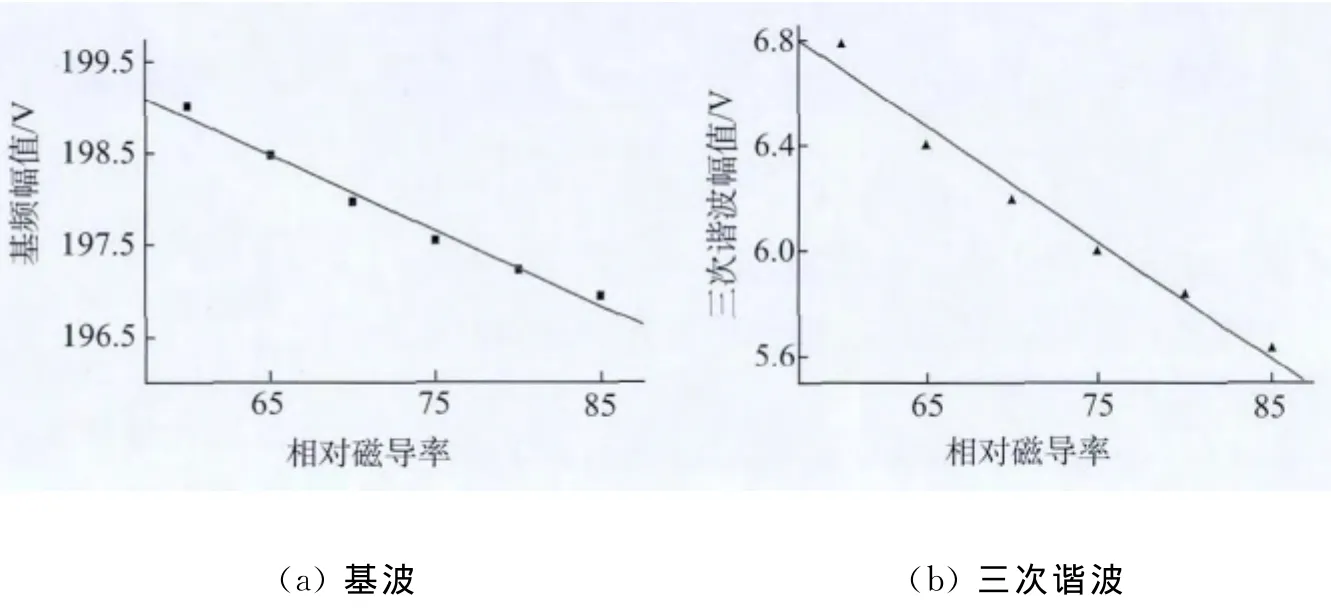
图6 基波与三次谐波幅值与塑性变形关系

4 结论

基于变形磁矢位（Ar）低频涡流场控制，采用Crank－Nicholson直接积分法改良开发了非线性涡流数值模拟程序。对一简化的磁性材料三维模型，以不同初始磁导率等效模拟材料不同程度塑性损伤，计算得到不同损伤程度下非线性涡流信号。提取信号中基波幅值和三次谐波幅值得出与塑性损伤之间关系曲线。通过对比该关系曲线与此前试验研究中碳素钢的试验检测结果是一致的，证明了塑性变形导致的磁导率变化是非线性涡流检测信号变化的直接诱因，也验证了非线性涡流检测对碳素钢等磁性材料塑性变形无损定量评价的可行性。

［1]SHIWA M，CHEN G Z，HORII Y，et al.Evaluation of PWHT temperature for Cr－Mo steel welded joint by AC magnetic signal analysis［J].Electromagnetic Nondestructive Evaluation，2006，Ⅶ：295－304.

［2]UCHIMOTO T，TAKAGI T.Characterization of matrices and graphite forms of cast irons by electromagnetic nondestructive evaluation［J].Electromagnetic Nondestructive Evaluation，2009，Ⅻ：207－214.

［3]STUPAKOV O，UCHIMOTO T，TAKAGI T，et al.Evaluation of ductile cast iron microstructure by magnetic hysteresis and barkhausen noise methods［J].E－lectromagnetic Nondestructive Evaluation，2009，Ⅻ：232－239.

［4]冯慈璋，马西奎.工程电磁场导论［M].北京：高等教育出版社，2006.

［5]何松，张辉，倪泽钧.常用钢材磁特性曲线速查手册［M].北京：机械工业出版社，2003.

［6]于庆波，李子林，韦玄，等.低碳合金钢变形奥氏体的相变研究［J].材料热处理学报，2007，28（4）：83－87.

［7]李维娟 ，李胜利 ，王方.奥氏体变形条件下低碳微合金钢中的贝氏体相变［J].金属热处理，2005，30（6）：70－73.

［8]李明，任爱，薛飞.铁磁性材料热交换管的远场涡流检测探讨［J].无损检测，2005，27（1）：6－9.

［9]周理平.涡流无损评价的理论与试验方法［J].无损检测，1996，18（7）：186－188.