三端式磁通门传感器研究

2014-05-14赵庆平姜恩华

唐山学院学报 2014年3期

赵庆平，邵芬，姜恩华

（淮北师范大学物理与电子信息学院，安徽淮北235000）

0 引言

磁通门传感器是一种应用于磁场测量的传感器。磁通门技术作为一种专业性的技术原本只应用于个别领域，且全世界仅有极少的国家掌握磁通门技术的开发。近年来，随着金属冶炼技术、计算机技术、物理学、电磁学等有关技术和学科的快速发展，使磁通门技术在弱磁场测量、抗干扰、智能化、性价比方面都得以改善，迅速普及到各个领域，如军事、航空、石油钻井、地质勘探等等。

由于磁通门技术的大力发展及广泛应用，使得对磁通门传感器的研究日趋成为磁测量方面的重要分支，本文将研究三端式磁通门探头的制作。根据已有资料、文献［1－3］，建立磁通门传感器工作原理的数学模型，从而确定影响磁通门探头性能指标的各个参数。通过改变影响这些参数的变量，制作不同的几组磁通门传感器探头，选择合适的检测电路测量，将得到的数据应用Matlab软件进行处理，再应用数学方法得到制作的磁通门的性能指标与现有的磁通门探头比较，分析其非线性度、分辨率、灵敏度和稳定性，拟为磁通门探头的设计提供参考。

1 磁通门探头的工作原理

在理想情况下，磁通门原理遵从法拉第电磁感应定律。下面通过数学模型法进行分析［4］。将线圈缠绕在骨架上，作为激磁线圈和感应线圈。线圈的匝数为M，铁芯的横截面积为S，铁芯磁导率为μ，线圈在铁芯上产生的磁场强度为H，产生的感应电势为ε。根据法拉第电磁感应定律

其中，k为常数，k＝10－8。如果铁芯和线圈保持不变，即S和M不变；铁芯在远离饱和的状态下工作时，即理想状态下，μ可以近似为一个不变的常数，则只有H的改变能够引起感应电势ε的改变。设激磁磁场频率为f，激磁磁场强度幅值为 Hm，H＝Hmcos 2πft，将其带入（1）式后得到

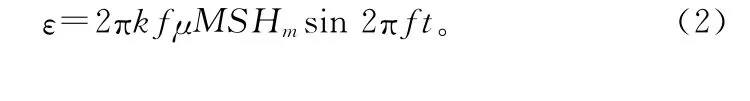
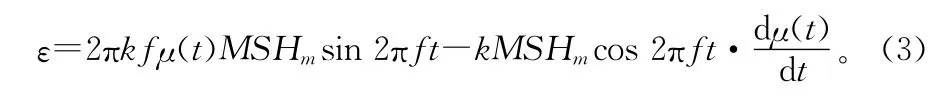
磁场强度H是随着时间周期性变化的，而磁导率μ（t）却没有正负区别，是偶函数，将μ（t）进行傅里叶级数展开得：其中，μ0m是常数分量值，μ2m，μ4m，μ6m，μ8m…则是各偶次谐波分量值。

将式（4）和式（3）联立，整理可以得到：

理想情况下，磁通门探头的数学模型就是（2）式，但因为实际上铁芯磁化曲线是非线性的，铁芯磁导率μ是随时变化的，即实际的模型公式应为：

从式（5）可以看出，当考虑了磁导率随铁芯磁场变化而产生的变化后，感应电势ε中出现了奇次谐波分量。

另外，由于环境中也存在着磁场，磁通门探头长轴比短轴长很多，所以可以看成是只感应其轴向上的磁场强度。设这一磁场强度为B，则式（3）可变化为：

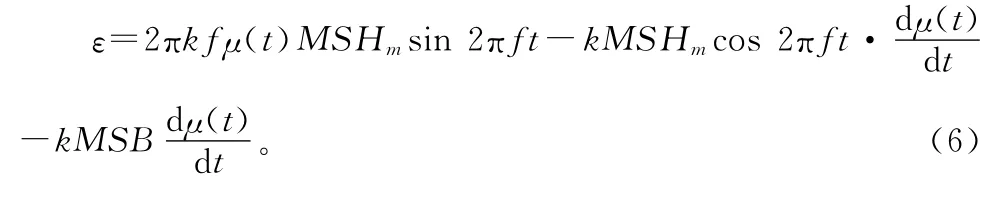
通常情况下，铁芯饱和时的磁场强度，激磁磁场的幅值Hm都要比环境磁场大很多，所以B对磁导率μ的影响很小，可忽略不计。式（6）最后一项产生的感应电势ε′为：

上式表明：激磁磁场强度变化，铁芯磁导率随之变化，感应电势ε就会产生随着周围环境磁场变化的感应电势ε′，属于偶次谐波量值。当铁芯工作在周期性的过饱和状态时，ε′将会显著地增大。显然，这一原理可被应用于测量周围环境的磁场。

2 总体方案设计

2．1 磁通门探头测磁电路方案设计

磁通门传感器要想达到测量磁场的目的，测试电路应主要包含3部分：激磁电路、传感器探头、检测电路。其原理框图如图1所示。

激磁电路选择：根据已有资料及文献［1－3］，激磁电路的频率、电压的幅值都对传感器的灵敏度和稳定性存在影响，同时，传感器探头磁芯必须工作在饱和状态下，因此对磁芯饱和角变化产生影响的波形要求稳定。所以驱动信号要求频率、相位、电压的幅值都相对稳定；测磁过程采用的有用信号是二次谐波信号，这要求电源电压中不应该含有偶次谐波信号。

图1 磁通门传感器测磁电路框图

综合以上考虑，本文激磁电路的驱动信号选用的是频率为4．7 k Hz的方波。

检测电路选择：磁通门探头将环境中的磁场转化成偶次谐波形式的磁通门信号，而检测电路则将通过功率放大、选频放大、相干检波、积分滤波一系列过程，将选择的二次谐波分量转化成模拟信号，这是一个开环系统。

2．2 磁通门探头特性测试电路方案设计

自制的传感器探头需要进行特性测试，为了尽可能避免噪声的干扰，需要在屏蔽室中进行以下的操作及测量［5－6］。

检测电路：闭环系统即是将磁通门探头的模拟输出信号反馈到探头线圈上，这样就会在探头上产生一个与原磁场方向相反的磁场，用于抵消原磁场，以保证探头工作在较弱磁场环境中。根据要求，设计测试电路如图2所示。

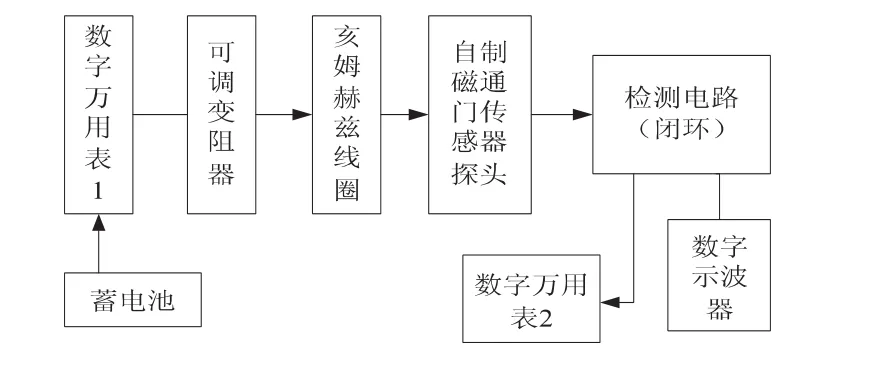
图2 磁通门传感器特性测试电路框图

图2中所示电路测量要求在尽可能减小干扰的情况下进行，所以，将探头在亥姆赫兹线圈中固定后，再将这一部分放入屏蔽桶中，与外界磁场阻隔，蓄电池选用12 V量程的即可。

3 磁通门传感器特性测试及数据处理

3．1 磁通门探头样机参数

通过以上的分析，设计并制作了5组三端式磁通门探头样机［7－8］，其参数如表1所示。

表1 自制磁通门探头参数

3．2 数据记录及Matlab处理

对于2．1节，用示波器显示所测得的输入信号波形，含有噪声的混叠信号波形，以及经过滤波处理后得到的输出信号波形，这一波形即外界环境磁场经过检测电路得到的波形。

对于2．2节，用万用表1测量电路的电流I，用万用表2测量检测电路端的电压U，记录数据，应用Matlab软件进行绘图，得到电流－电压的特性曲线，并进行最小二乘拟合，最后应用数学方法进行计算，得到自制磁通门探头的性能指标。

记录波形如下：输入的激磁信号波形如图3所示，经过磁通门探头的输出信号如图4所示，检测电路输出信号如图5所示。

图3 激磁信号

图4 探头输出信号

图5 检测电路输出信号

在屏蔽室中利用2．2节方法进行处理，测得5组数据记录如表2所示。第6组表示已有的探头数据，用以作为对照组。其中，Xi表示各组传感器探头的输入电流，量程为200 m A，Yi表示检测电路的输出电压，量程为20 V。

表2 传感器电流－电压数据

用Matlab软件进行最小二乘拟合处理，得到电压－电流特性曲线，是一条直线，各组传感器探头拟合直线的斜率分别为Ki，如表3所示。

表3 二乘拟合直线斜率

Matlab拟合后的直线如图6所示。图6中，从上往下颜色标注依次是红、蓝、黄、绿、亮青，对应探头标号是第2组、第5组、第3组、第1组、第4组；最下面一条黑色直线是已有探头成品，用于对照。

3．3 测试结果分析

非线性度：计算公式为γ＝Δy／Y，其中，Δy为实际电压值减去相对应的拟合后电压值后的最小值，Y为实际电压最大值与最小值的差。

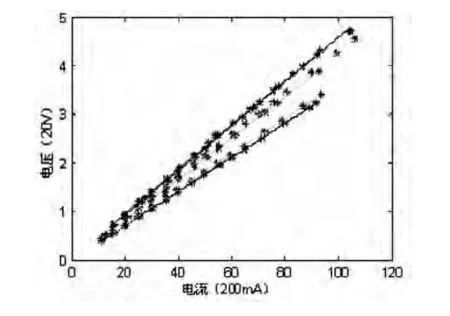
图6 Matlab最小二乘拟合图

由于非线性度测量对数据要求准确，所以采用了七位半的万用表，各组传感非线性度计算结果γ1＝0．092 3%，γ2＝0．115%，γ3＝0．092%，γ4＝0．086%，γ5＝0．115%。由此可以看出第1，3，4组自制传感器探头的实际值与拟合直线间的偏差较小一些，非线性度较好，能达到0．1%以下。

分辨率：分辨率是指传感器能检测到的最小输入增量，由于本设计的磁通门探头的分辨率较高，所以采用七位半的万用表，利用2．2节的电路测输出电压。当输入电流连续变化时，输出电压的最小变化量即为分辨率。对非线性度良好的3组进行分辨率测量，结果：第1组传感器约为6．1 n T，第3组传感器约为5．6 n T，第4组传感器约为4．2 n T。

稳定性：稳定性误差是指传感器探头在长时间工作的情况下输出电压的变化。测试时，记下传感器的输出电压的某一定点，工作一段时间，读出此时的电压值，两次电压之间的变化即为稳定性误差。工作时间为1 h，第1组传感器稳定性误差不大于50 n T，第3组传感器稳定性误差不大于30 n T，第4组传感器不大于45 n T。

灵敏度：传感器输出变化量与引起它变化的输入变化量之间的比值Δy／Δx即为灵敏度k，由于用的是同一个亥姆赫兹线圈，其系数a＝503 n T／mA，则第1组传感的灵敏度k1＝0．084 mV／nT，第2组传感器的灵敏度为k2＝0．09 mV／n T，第3组传感器灵敏度k3＝0．09 mV／n T，第4组传感器灵敏度k4＝0．073 mV／nT，第5组传感器灵敏度k＝0．091 mV／nT。

功耗：用万用表测量激磁电路输入端的电流，由于本文中所应用的电路有5块电路板，所以粗略计算时，可直接用测得的电流除以5，即为功耗。计算结果：第1组传感器功耗为32 m A／路，第3组传感器功耗为30 m A／路，第4组传感器功耗为28 m A／路。

数据综合分析：由于自制传感器的线圈采用了手工缠绕，不可能完全达到对称，所以测试结果存在一定误差。不过，整体趋势不变。对于第1组和第3组传感器，比较非线性度、稳定性可知，在铁芯横截面积、材料、激磁电源频率相同，线圈匝数变化微小的情况下，铁芯细长比小的，对其稳定度有利，对其灵敏度不利；比较第1组和第4组传感器可知，线圈的匝数增加，在磁通门探头的灵敏度增加的同时，探头的输出噪声也会增加，漏磁现象也可能更严重，稳定性及动态性能受到影响，这些都比较符合理论分析的结论。因此线圈的匝数的改变确实可以用来减小磁通门探头的噪声信号，但并不能完全消除噪声。