基于混沌蚁群算法的地震应急物流配送路径优化问题研究

刘金雨，刘亚敏，连 浩，张佳惠，王 娟

(防灾科技学院防灾仪器系，北京 101601)

近年来，我国地震频发，快捷有效开展灾后救援已成为近年来的研究重点。但目前大多数混沌蚁群算法只局限于定性分析及保障机制［1］，缺乏定量研究。本文采用混沌蚁群算法对数学模型进行求解，提高了基本蚁群算法的全局搜索能力及收敛速度。仿真试验验证了算法的可行性及有效性。

1 地震应急物流配送路径优化

1.1 问题阐述

地震救灾物资的运输需求具有突发性和局部性，因此地震救援需要考虑环境时间等因素。本文以地震救援物资运送到各个地震受灾点时间最短为目标，引入路况系数及地震救援物资紧缺系数来分别表征道路损坏程度及救援物资紧缺程度，其中路况系数与道路损坏程度成正比，地震救援物资紧缺系数与救援车辆配送效率成正比。

1.2 地震应急物流配送路径优化模型

基于混沌蚁群算法的数学模型假设如下:

1)单一的地震救灾物资配送中心作为地震应急救援车辆起点及终点。

2)每次配送中，地震救援车辆所载物资小于等于地震救援车辆的已知最大载重量，途中无装货。

3)地震受灾点的位置和需求量已知且需求量不超过地震救援车辆的最大载重量。

4)地震救援车辆平均行驶速度已知且确定。

5)地震应急运输救援车辆必须在要求时间内到达，否则，优化路径将被放弃。

基于上述假设，数学模型以配送时间最短为目标，如下:

S.T.

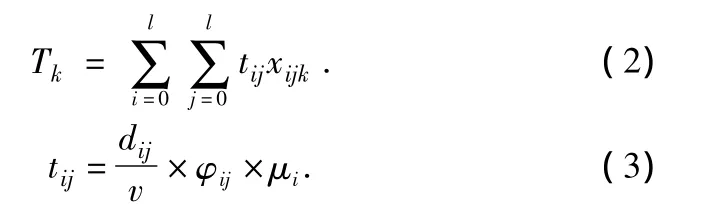
其中，地震救援车辆总数为m';地震受灾点总个数为l;i与j点之间的总距离为dij;地震救援车辆k行驶的总时长为Tk;tij为地震救援车辆从地震受灾点i到地震受灾点j行驶的总时长;gi为第i个地震受灾点的总物资需求量;地震救援车辆最大载重量限制为q;地震救援车辆编号为k;地震物资救援车辆行驶速度为v;灾后路况系数为φij;灾后医疗器械紧缺程度用系数μi表示;tjk为地震救援车辆k到达受灾点i点的总时长;最大地震受灾点配送时间为tei。

1，2，3，…，l为地震受灾点编号，0，1，…为地震救灾物资配送中心编号，定义变量xijk，yki为:

式(1)是以时间最少为目标函数的数学模型。式(2)为地震救援车辆k行驶总时长;式(3)为在加入每个地震受灾点的路况情况和物资紧缺程度后，地震救援车辆行驶经过地震受灾点i，j所需要总时长;式(4)地震救援物资总重量小于等于地震救援车辆最大载重;式(5)、式(6)和式(7)有且仅有一救援车辆经过单一地震受灾点。式(8)为第k辆车经过i转移完成第j需求点任务;式(9)为第k辆车经过j转移完成第i需求点任务。式(10)确保全部救援车辆出发点及终点为地震救灾物资配送中心。式(11)为物资到达地震受灾点时长限制。

2 混沌蚁群算法求解模型

Step1

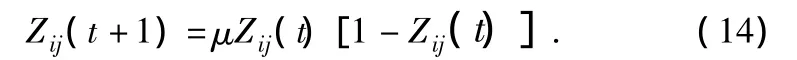
式中 μ 为控制参数，取值区间［3.56，4］［2］;信息素初始值由混沌量确定。

Step2由(15)计算蚂蚁k的转移概率。

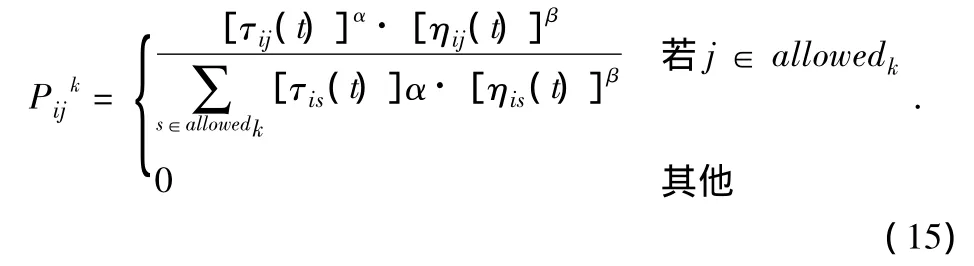
式中，allowedk=(1，2，…，n)－tabuk为蚂蚁 k当前能选择集合;tabuk(k=1，2，…，m)表示蚂蚁 k的禁忌表，ηij(t)为启发函数，一般选ηij(t)=1/dij;α为路径ij上残留信息的重要程度，β为启发信息的重要程度。

Step3根据转移概率转移到下一个救灾点j，同时将j加入tabuk中。如果车辆载重达到上限，车辆返回地震救灾物资配送中心;

Step4检查tabuk是否满。若为否，回到step 2，否则，继续step 5;

Step5计算目标函数和Tk，并记录当前最优解;

Step6

上式为信息素更新，Zij(t)是混沌变量。q1为系数。ρ表示全局信息素挥发因子(0，1)［3］。Δτij(t)表示本次周游中路径ij信息素增量。

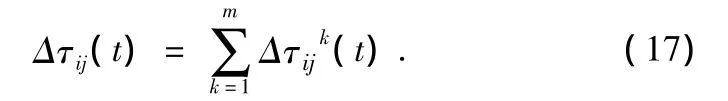
Step7若 NC ＜NCmaxNC=NC+1，清空 tabuk，回到 step 2。若 NC=NCmax，结束。

3 实验仿真

假定灾后4辆救援车向19个地震受灾点运送地震救灾物资。救援车辆最大装载重为90 t，速度为60 km/h。表1为各个地震救援路径优化实验数据。选α=1，β=5，ρ=0.6［4］，混沌变量 Zij(0)=0.5，q1=1。地震受灾点与地震救灾物资配送中心之间的距离计算如下式:

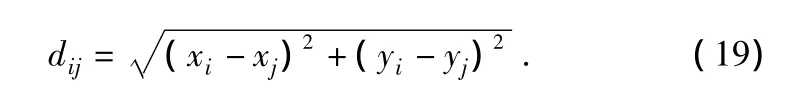
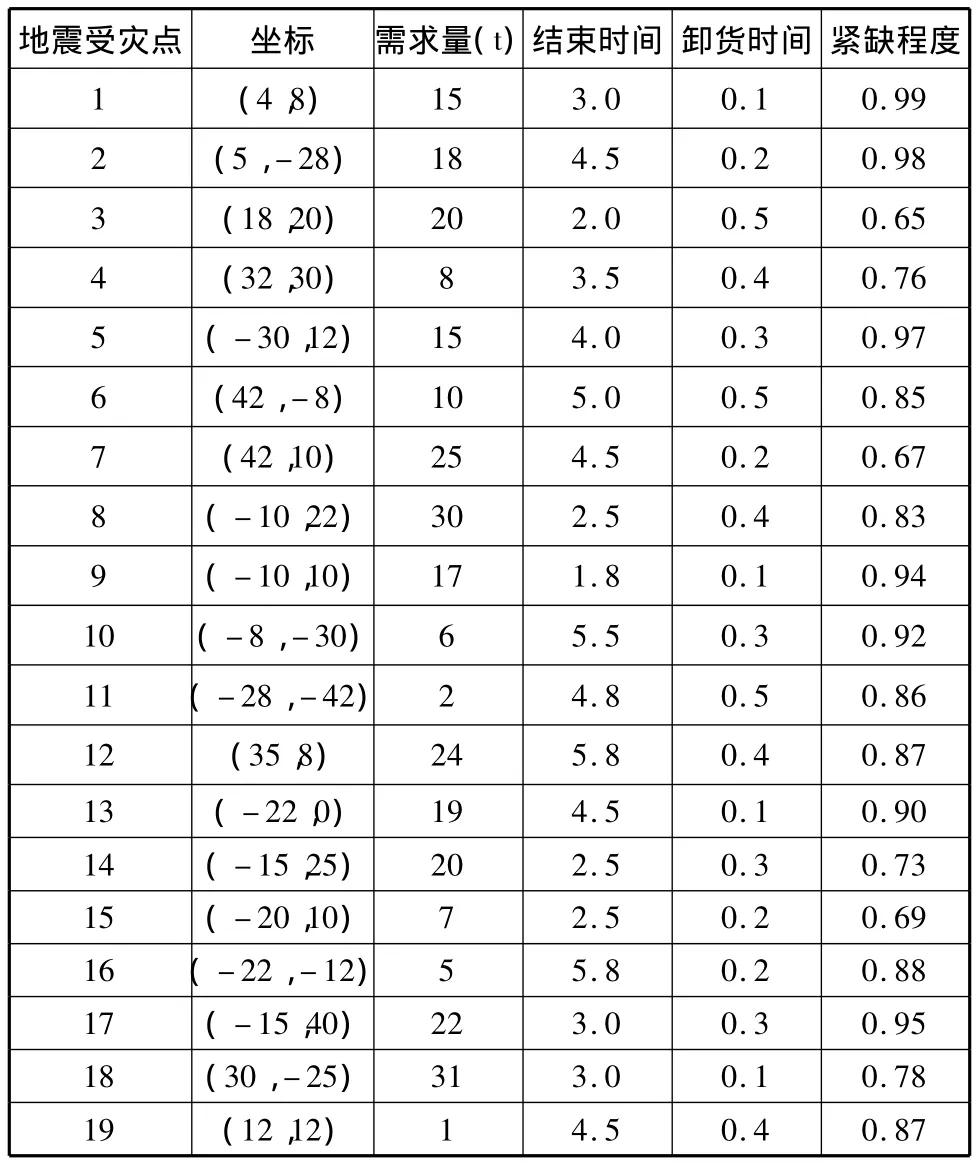
表1 实验数据

图1，图2分别给出4辆救援车基于混沌蚁群算法和基本蚁群算法的运行路线图的最优解寻优路线。由图可以看出混沌蚁群算法所需配送时间远小于基本蚁群算法所需的配送时间。这是由于引入混沌概念，增加了蚂蚁的历遍性，近而避免基本蚁群算法过早收敛及陷于局部最优的不足。

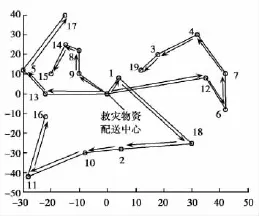
图1 混沌蚁群算法运行路线图

图2 基本蚁群算法运行路线图

6 结束语

混沌蚁群算法利用了历遍性优化搜索［6］，在地震应急物流路径优化问题上优于基本蚁群算法。本文数学模型考虑的实际条件还不是很全面，今后对于地震应急物流路径优化问题的模型建立还需要进一步的完善和充实。

［1］冯旭东，率帅.抓好应急物流配送的几项对策［J］.中国物流与采购，2003，23(3):31 －34.

［2］高尚.旅行商问题的混沌蚁群算法［J］.系统工程理论与实践，2005，8(9):100 －103.

［3］刘立东.改进蚁群优化算法的研究［D］.成都:西南交通大学，2005.

［4］叶志伟，郑肇葆.蚁群算法中参数 α，β，设置的研究——以TSP问题为例［J］.武汉大学学报(信息科学版)，2004，29(7):597 －601.

［5］Dorigo M.Ant Colony System:A Cooperative Learning Approach to the Traveling Salesman Problem［J］.IEEE Transactions on Evolutionary Computation，1997，1(1):53－66.

［6］Reimann M，Doerner K，Riehard FH.D －Ants:Savings Based Ants Divide and Conquer the Vehicle Routing Problem［J］.Computers and Operations Research，2004，31(2):563－591.