基于液压传动系统的风电并网静态电压稳定问题研究

卢鹏铭，温步瀛

（福州大学电气工程与自动化学院，福建福州 350108）

近年来，风力发电作为一种清洁能源迅速发展，而风能具有随机性和间歇性特点，使得风电的运行特性不同于常规电源，其输出的功率取决于风速的大小，具有随机性、波动性和难以控制性，且单机容量小，往往是大量风力发电机组并列运行，大量风电场的接入对电网的稳定运行带来了一定的影响[1-6]。变速型风力发电机组具有较高的运行效率，且可以调节发电机输出功率因数，在风电场中得到广泛应用，但其出力仍然是间歇、波动和难以控制的。因此，风力发电的并网稳定问题一直是风电产业进一步发展的瓶颈。基于液压传动系统的风力发电机组采用液压柔性的传动，使得一定范围内的风速变动保持风力发电机输出功率的稳定性，从根本上解决了并网的稳定性难题。

1 基于液压传动系统的风力发电建模

基于液压传动系统的风力发电机与常见的恒频恒速风力发电机构造类似，不过基于液压传动系统的风力发电系统采用液压传动系统替代了常规风力发电机中的齿轮箱传动系统[7]。图1为基于液压传动系统的风力发电机系统结构图。

基于液压传动系统的风力发电机建模主要是对其液压传动系统模型的建立，其他部件的模型与普通异步风力发电机[8-9]一样，组成部分如图1所示。

图1 基于液压传动系统的风力发电机系统结构图Fig.1 The system structure of w ind turbines based on hydraulic drive

1.1 风力机模型

风力机通过捕获风能将风能转换成机械能，风力机的机械功率仿真数学模型如式（1）所示[10]。

式中，PM为风力机输出的机械功率；V为风速；Vin、VN和Vout分别为风力机切入风速，额定风速和切出风速；R为风力机的叶片半径；λw为叶尖速比（λw=ωR/V）；ω为风力机转速；β为桨距角；CP为风力机转换效率系数。

机械转矩为：

式中，MT为风力机的机械转矩。

1.2 传动部分模型

采用液压传动的风力发电机机械传动部分一般包含轮毂、液压系统和联轴器。叶片的风能转矩传递到轮毂存在的时滞，可以用式（3）的一阶惯性模型来表示。

式中，Ml为轮毂转矩；Ts为时滞时间系数。

液压泵的流量方程为：

式中，Qp0和Qp1分别为泵的理论和泄漏流量，且Qp0=qpnp/60；qp和nP分别为液压泵的流量和转速；Qp1=Clppp；Clp为液压泵的泄漏系数；pp为液压泵内部压力。图2为液压泵环节的仿真模型框图。

图2 液压泵环节的仿真模型框图Fig.2 Block diagram of the simulation model of the hydraulic pum p parts

通过对泵的转矩Tp的调节可以实现对叶轮的转速的控制：

式中，pp、qp和ηpm分别为泵的压力、排量和机械效率。

液压泵、蓄能器和液压马达三者之间的连续性流量方程为：

式中，px、Vx和Qx分别为蓄能器内的压力、液体体积和流量；Ex为有效体积弹性模量；Qm为液压马达的实际流量。图3为蓄能器环节的仿真框图。

图3 蓄能器环节的仿真模型框图Fig.3 Block diagram of the simulation model of the accumulator

液压马达的流量方程为：

式中，Qm0和Qm1分别为液压马达的理论流量和泄漏流量，且Qm0=qmnm/60；qm和nm分别为马达流量和马达转速，Qm1=Cmppm；Cmp为液压马达的泄漏系数；pm为马达内部压力。图4为液压马达流量连续方程的仿真框图。

图4 液压马达流量连续方程的仿真模型框图Fig.4 Simulation block diagram of the hydraulic motor flow continuity equation

液压马达的轴系力矩平衡方程为：

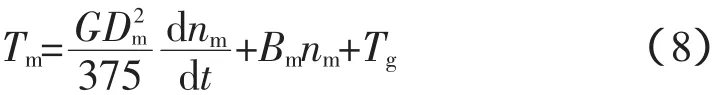
式中，GDm2、Bm和nm分别为液压马达轴系上的飞轮惯量、黏性阻尼系数和转速；Tg为传递到发电机的转矩。图5为液压马达轴系力矩平衡方程的仿真框图。

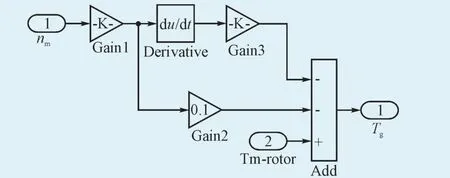
图5 液压马达轴系力矩平衡方程的仿真模型框图Fig.5 Simulation block diagram of the hydraulic motor shaft torque balance equation

2 基于液压传动系统的风力发电机仿真运行特性分析

有研究表明异步的快速响应特性会影响并网的静态和暂态电压稳定性。而目前风电场大部分的发电机组都是采用异步发电机，因此风电场的运行会对整个系统的电压稳定性造成影响[11-14]。由于异步机的快速响应特性，风速的闪变可能会影响整个系统的暂态电压稳定性。因此，本节主要分析在低风速情况和额定风速情况下，对比风速变化对普通风力发电机和基于液压传动系统的风力发电机输出的影响来研究液压传动系统的风电并网的输出功率特性。取普通风力发电机和基于液压传动风力发电机的额定风速均为13 m/s，切入和切出风速分别为3 m/s和25 m/s，额定功率均为600 kW。图6和9分别是平均风速为额定风速和低风速情况下的风速变化图，图7、8、10和11分别是这两种情况下的普通风力发电机和基于液压传动风力发电机的输出功率仿真图。

图6 30 s风速变化情况Fig.6 The w ind speed changes（30 seconds）

图7 普通异步风力发电机输出功率Fig.7 The output power of ordinary asynchronous w ind generator

图8 基于液压传动系统的风力发电机输出功率Fig.8 The output power of the w ind generator based on hydraulic system

图9 30 s风速变化情况（低风速）Fig.9 The w ind speed changes（Low w ind speed）

通过上图的对比可以看出液压传动系统作用下的风力发电机不管在低风速或者额定风速的情况下均能保持输出功率的稳定性，因此可以看出基于液压传动系统的风力发电机组在运行过程中能在风速变化情况下，保障了输出功率的稳定性。相比于低风速情况，额定风速下，风力发电机组的输出更为稳定。相比于陆上风电场，基于液压传动系统的风电的输出稳定，更适合用于近年来兴起的海上风力发电。海上风电输出风速较为稳定，平均风速高于陆地，而海上风电的投资项目主要增加了机座和海底电缆的架设，其他成本和陆上风电基本一致，液压系统的灵活和轻便，令其与其他风电机相比更易于安装，风电机内部结构的布置更加合理。同时，液压系统具有的耐用、故障率低也解决了海上风电安装和维护难度大问题。

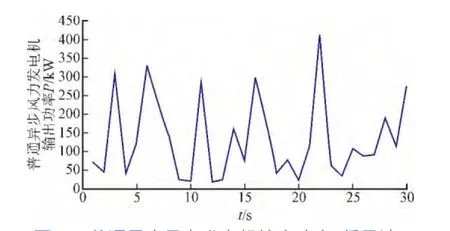
图10 普通异步风力发电机输出功率（低风速）Fig.10 The output power of ordinary asynchronous w ind generator（Low w ind speed）

图11 基于液压传动系统的风力发电机输出功率（低风速）Fig.11 The output power of the wind generator based on hydraulic system（Low w ind speed）

3 基于液压传动系统的风电并网静态电压稳定分析

电力系统对电压稳定问题的研究主要包含静态电压稳定性和暂态电压稳定性，分别研究系统受到小扰动和大扰动（故障）时的电压稳定问题。

3.1 风电场并网静态电压稳定性分析

连续潮流法是从系统初始点开始，随着按照定步长缓慢增加负荷，沿着当前曲线通过预估、校正得到下个工作点的值，直到画出完整的P-V曲线[15-16]。为了缩短计算时间和提高解的收敛性，本文采用改进的连续潮流算法，即将常规的潮流算法和连续潮流算法相结合。其基本方程为：

或

式中，f（x）为常规潮流计算方程；b和λ分别为所分析系统中各节点负荷的增长方式和增长参数，λ（0≤λ≤λcr，即负荷在临界点以内增加；λcr为临界负荷增长参数）；x为系统的状态变量（取决于待求节点电压相角、幅值及负荷的增长参数）；δ和V为分别为待求节点电压相角和幅值。将负荷带增长系统的负荷代入常规潮流计算方程得：

式中，PGi0、QGi0和PLi0、QLi0分别为节点i的有功、无功输出和有功、无功负荷；Vi和δi分别为节点i的电压幅值和相角；yij<γij为节点导纳矩阵中的第（i，j）个元素；KGi和KLi分别为发电机输出有功和负荷功率的变化率系数；ψi为节点i负荷变化的功率因数角；SB为视在功率的基准值，

连续潮流法经过预估和校正两个步骤后得出随负荷参数变化的潮流解。图12为连续潮流计算的直观原理图。

3.1.1 预估

采用线性化估计沿着修正后的连续潮流的切向量方向延伸来寻找预解，也就是对常规基本方程式（13）求偏导得到线性化的增量方程：修正后的连续潮流的切向量方向。

由于在潮流方程中引入了负荷增长系数λ，则增加了一个待求量，要满足解潮流方程的条件可以通过将切向量的第k个分量定为1或者-1，并将设定的分量称为连续分量。通过下式对切向量求解：

式中，ek为第k个元素为1，其他元素都为0的行向量。

在解得切向量的基础上进行解的预估：

式中，δ*、V*和λ*分别为δ、V和λ的预估值；σ为步长。

3.1.2 校正

将上一步求得的预估值代入引入附加方程的扩展潮流方程，并使用牛顿-拉夫逊法迭代来求得校正值。

式中，xk为待求量的第k个分量，该值已由预测值确定；η为预测值的第k个分量。

图13为牛顿-拉夫逊法连续潮流计算的程序流程图。

3.2 基于液压传动系统的风电并网静态电压稳定性分析

本文采用对3种情形下系统参数的对比研究基于液压传动系统的风电并网静态电压稳定性。情形一：对IEEE-9节点标准系统的分析；情形二：系统节点3的85 MW传统发电机Gen 3采用150台额定功率同为600 kW的基于液压传动系统的风力发电机构成的风电场替代；情形三：系统节点3的85 MW传统发电机Gen 3采用200台额定功率同为600 kW的基于液压传动系统的风力发电机构成的风电场替代。对情形二和情形三的分析均忽略风电场内部损耗，并分别从系统正常稳定运行状态和极限负荷运行状态两种不同运行方式进行研究。图14为IEEE-9标准系统接线图。系统正常运行时，情形一、二、三所对应的各节点电压值如表1所示。

通过牛顿-拉夫逊连续潮流法，对两种情况采用同比例负荷增长，步长统一取0.05，分别算得在极限负荷运行状态时的标准IEEE_9系统和接入基于液压传动系统的风电场后的系统各节点电压值和负荷裕度变化情况，如表2所示。3种情况下所对应的PV曲线如图15所示。

图13 牛顿-拉夫逊法连续潮流计算的程序流程图Fig.13 The program flow chart of New ton-Raphson continuous power flow calculation

图14 IEEE-9标准系统接线图Fig.14 The system w iring diagram of IEEE-9

通过所得出的PV曲线可以看出，在未接入液压传动的风力发电机组时，系统节点9为敏感节点，在增加负荷功率时，最先出现节点电压崩溃，而接入液压传动的风力发电机组后节点3（风电机组接入点）最先出现电压崩溃。由表1和表2的所得的数据可以看出基于液压传动系统的风电场接入系统后会引起系统负荷裕度的降低，即降低了系统的静态电压稳定性。从表1的数据可以看出正常运行状态下，接入风电场的数目越多，系统的电压水平越低，同时风电场的电压降低速度比其他节点更快，主要是因为风电场节点的电压水平取决于并网点的电压，系统阻抗比不变有功输出较大就使得风电场的电压较高。而风电场数目增加到一定数目时，由于风电机组相比于传统同步发电机，需要从系统吸收一定量的无功，当系统无功Q达到一定水平时就会引起系统整体功率因数下降，从而使得风电机组及所在系统的负荷电压下降。表2可以看出由于风电场的电压急剧下降，导致系统的负荷裕度减少，从而降低了系统的静态电压稳定性，并且并网风电的数量越多，系统电压的下降速度越快，负荷裕度越低，因此为了系统的整体稳定性，应该控制接入风电场的数目。

表1 系统正常稳定运行状态下的风电并网前后的IEEE_9节点电压值Tab.1 IEEE_9 node voltage values before and after integration w ith the power grid under normal steady state operation

表2 系统极限负荷运行状态下的基于液压传动系统的风电并网前后的IEEE_9负荷节点电压值及系统负荷裕度Tab.2 IEEE_9 load node voltage value and the system load margin before and after integration of w ind power w ith the power grid under the lim ited load operation mode

图15 系统PV曲线图Fig.15 The system PV curve

4 结论

本文针对基于液压传动系统的风力发电系统进行并网静态电压稳定性研究，由所得的结果可以看出液压传动的风力发电机能在风速变化的情况下，保持输出的稳定性，大大提高了风电并网时输出功率的稳定性，但是由于采用异步风力发电机并网时会影响系统的静态电压稳定性。因此，应该控制采用异步发电机的基于液压传动系统的风力发电机的并网数量。

[1] 国家电网公司.各区域电网装机容量[EB/OL].http://www.sgcc.corn.cn.2013-03-10.

[2] Global Wind Energy Council.GWEC releases global wind 2007 Report[EB/OL].http://www.gwec.net.2008-04-01.

[3] 孙涛，王伟胜，戴慧珠.风力发电引起的电压波动和闪变[J].电网技术，2003，27（12）：62-66.SUN Tao，WANG Weisheng，DAI Huizhu.Voltage fluctuation and flicker caused by wind power feneration[J].PowerSystem Tchnology，2003，27（12）:62-66（inChinese）.

[4] 李智，顾菊平，张新松，等.风功率不确定性对电网的影响及其应对措施[J].电网与清洁能源，2013，29（8）：68-74.LI Zhi，GU Juping，ZHANG Xinsong，et al.Impacts of wind power uncertainties on power grid and corresponding countermeasures[J].Power System and Clean Energy，2013，29（8）:68-74（in Chinese）.

[5] 米增强，田建设，刘力丰.低压减载对电压稳定作用机理的探讨[J].华北电力大学学报，1999，26（1）:31-36.MI Zengqiang，TIAN Jianshe，LIU Lifeng.Research on the mechanism of under-voltage load shedding in respect of voltage stability[J].Journal of North China Electric Power University，1999，26（1）:31-36（in Chinese）.

[6] 闫广新，李江，张锋，等.变速双馈风电机组低电压穿越功能仿真[J].电网与清洁能源，2009，25（6）：49-52.YAN Guangxin，LI Jiang，ZHANG Feng，et al.Functional simulation for low voltage ride through capability of DFIG for wind turbines[J].Power System and Clean Energy，2009，25（6）:49-52（in Chinese）.

[7] 陈建业，周强.液压传动在风力发电系统中的应用[J].移动电源和车辆，2011（1）：30-32.CHEN Jianye，ZHOU Qiang.Application of hydraulic drive in wind power generation system[J].Movable Power Station&Vehicle，2011（1）:30-32（in Chinese）.

[8] 牛晨光，刘观起.双馈感应异步风力发电机组的低电压穿越求及技术分析[J].电网与清洁能源，2011，27（8）：77-83.NIU Chenguang，LIU Guanqi.Low voltage ride through requirements and technical analysis of doublyfed induction wind turbines[J].Power System and Clean Energy，2011，27（8）:77-83（in Chinese）.

[9] 陕华平，肖登明，薛爱东.大型风电场的风资源评估[J].华东电力，2006，34（2）：15-18.SHAN Huaping，XIAO Dengming，XUE Aidong.Wind resource assessment for large wind power fields[J].East China Electric Power，2006，34（2）:15-18（in Chinese）.

[10] 吴旭，林俐.基于普通异步发电机的恒速风电机组模型与并网分析[J].电力技术，2010，19（3）：36-41.WU Xu，LIN Li.Model on constant speed wind turbine based on common asynchronous generator and its interconnection with power grid[J].Electric Power Technology，2010，19（3）:36-41（in Chinese）.

[11] 潘文霞.大型风电场电压稳定性分析与控制研究[D].南京：河海大学，2004.

[12] EL-SAADAWI M M，KADDAH SS，OSMAN M G，et al.Impact of wind farms on contingent power system voltage stability[C]//12th International Middle-East Power System Conference，12-15 March 2008，Aswan:637-644.

[13] Soren Krohn，Poul-Erik Morthorst，Shimon Awerbuch.The economics of wind energy[J].European Wind Energy Association，March 2009.

[14] 范李平，杨力森，武粉桃.风电场并网对电力系统稳定性影响[J].电网与清洁能源，2009，25（6）：58-61.FAN Liping，YANG Lisen，WU Fentao.Influence of wind farm interconnected to power grid on stability of power system[J].Power System and Clean Energy，2009，25（6）:58-61（in Chinese）.

[15] 廖成滨，温步瀛，江岳文，等.风电并网的静态电压稳定性研究[J].电网与清洁能源，2010，26（12）：85-90.LIAO Chengbin，WEN Buying，JIANG Yuewen，et al.Static voltage stability with wind power integrated with power grid[J].Power System and Clean Energy，2010，26（12）:85-90（in Chinese）.

[16] 庞汉飞.改进潮流算法在电压稳定分析中的应用[J].广东电力，2006，19（8）：8-11.PANG Hanfei.Using improved power flow method in voltage stability analysis[J].Guangdong Electric Power，2006，19（8）:8-11（in Chinese）.