应急决策信息系统最优路径研究——基于路阻函数理论及Dijkstra算法*

刘春年，邓青菁

（南昌大学信息工程学院，江西南昌330031）

应急决策信息系统最优路径研究
——基于路阻函数理论及Dijkstra算法*

刘春年，邓青菁

（南昌大学信息工程学院，江西南昌330031）

应急决策信息系统最优路径理论与实践研究是灾害应急信息化工程领域的重要分支和重点研究课题，将路阻函数理论与Dijkstra算法引入应急决策信息系统最优路径研究领域是一个持续引入关注并且具有显著价值的研究课题。围绕应急决策信息系统最优路径推理与求解，以Dijkstra算法为总体技术方法，以路阻函数理论为实时路段的路径权值提取技术基础，以应急决策相关主体的实际决策需求为中心，探索应急决策信息系统最优路径求解机制及其应用的理论技术基础及问题对策，提出了基于路阻函数理论与Dijkstra算法的最优路径数学模型，并以实例计算说明模型算法的有效性。在复杂的灾害交通环境下，该研究思路能更加充分有效的结合具体的灾害实时道路状况来提供灾害中受灾群众最优撤退路径。

应急决策信息系统；路阻函数理论；Dijkstra算法；路径优化

进入2l世纪，世界范围频发的突发事件预示着风险社会的来临。有数据显示，2000－2010年，中国每年受到自然灾害的平均次数为37 441.8次，每年人员伤亡数平均为47 407.8人次，平均直接经济损失达9 949 588.273万元（表1）。据统计，1965－1992年之间，世界上有超过10人以上死亡或100人以上受灾的自然灾害共4 653次。并且，此年间受灾人口共高达30亿，360万的人们死于自然灾害，造成的直接经济损失高达3 400亿美元。近30年来，自然灾害的发生频率、受到灾害影响的人数和灾害造成的直接经济损失都在迅速增长［1－4］。要减少突发事件和自然灾害带来的不可估量的人员伤亡和财产损失，应急决策信息系统的建设显得尤为关键。应急决策信息系统是整个应急体系建设中的重要基础，它在平时应急管理和事件突发后的应急响应过程中都发挥必不可少的保障作用。

针对应急决策信息系统所涉及的海量、异构、实时数据，研究对这些信息进行收集获取、数据分析、传播、可视化和共享等信息处理科学问题，已成为国内外研究热点，并有一些研究进展，主要包括灾害信息预警研究［5］、灾害信息传播研究［6］、灾害信息图谱研究［7］、信息扩散研究［8］、灾害信息挖掘研究［9］、灾害管理信息系统及决策支持信息系统的决策机制研究［10］、灾害信息识别研究［11］、数据标准化研究［12］、灾害信息公开及信息发布研究［13］、面向自然灾害的应急物流信息系统研究［14］、危机管理中情报活动及情报功能研究［15］等。

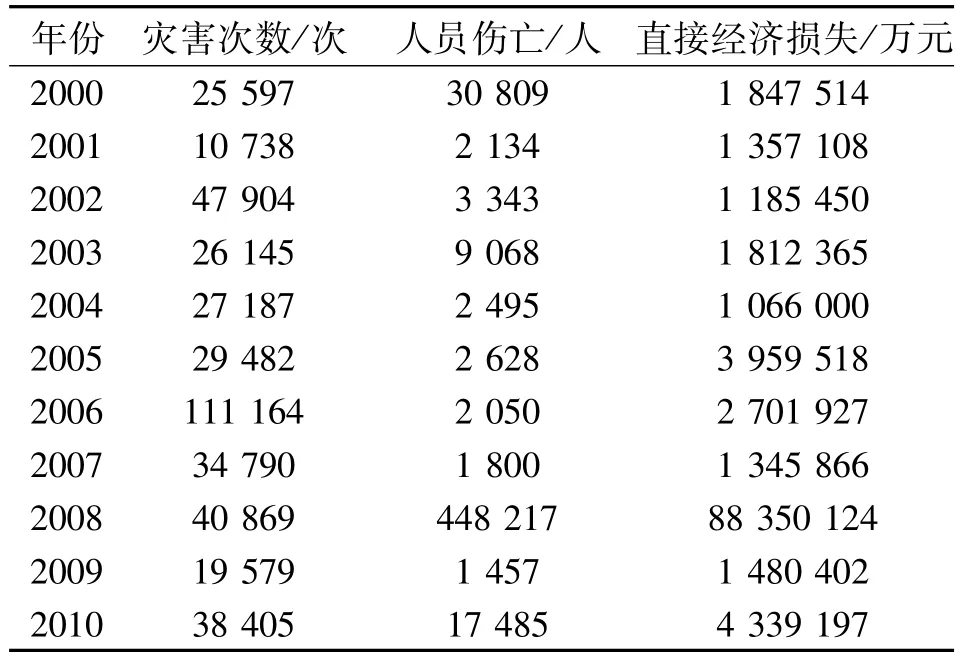
表1 中国历年自然灾害情况

应急系统的一项重要任务就是决定城市应急运输路线，要求发生事故时，救援者能以最快的速度到达现场进行救援。传统的车辆路径问题（Vehicle Routing Problem，VRP）是为运输物资的车辆设计最佳路径，使其总运输费用最小。Vigo、Laporte建立了多种变形的VRP模型，并给出了相应的算法［16－17］。与传统的VRP相比，应急物资调运主要是应急车辆在最短的时间内把应急物资由应急服务点运送到需求点，其研究的核心是最短路径选择问题。近年来，随着应急管理的推广实施，应急物资调度中的车辆路径选择与优化，成为该领域的一个新的热点。

应急资源调度属于灾害风险管理问题，一般而言是在已有应急资源上，为实现某种目标对其进行合理调度；通常考虑的是如何调动应急服务网点，以便使应急地点一旦发生自然灾害，应急服务网点能在最短的时间内或以最小的成本代价等对受灾地点实施救援，围绕这一问题，国内外许多学者进行过研究，取得了许多研究成果［18－19］。有的文献以最小化运输费用为决策目标构造模型，考虑了救援过程的经济性，但却未考虑灾害刚发生时救灾的迫切性及其对减灾的影响［20－21］；有的文献虽然考虑了救援延迟时间，并建立了以最小化需求满足延迟函数为目标函数的数学模型［22－23］，但却未考虑到灾害救援过程中，应急资源的调度应当与灾情相符，决策目标的确定，需从实际出发，因需要和条件的不同而异，方可对有限的资源进行合理调配；有的作者按照应急救援是以追求时间效益最大化、灾害损失为辅，并考虑使社会成本最小的特种物流活动［24］。总之，为减轻灾害带来的损失，研究应急决策信息系统路径优化问题具有特殊的重要意义。当发生紧急灾害时，受灾群众应该迅速撤退到事先选定的安置点处，受灾群众在灾害后的最优撤退路径问题是灾害应急决策信息系统研究的问题之一。

本文主要结合运用路阻函数理论和Dijkstra算法来对最佳撤退路径进行研究。国内外的学者对路阻函数理论和Dijkstra算法进行了深入的研究。如周继彪等针对交通流由畅通状态到拥挤状态再到堵塞状态的过程，应用经典交通流理论和实际调查数据，构建了交通流诱导系统分段路阻函数模型［25］；如刘宁等在美国BPR函数的基础上，引入影响车流通行时间的交叉口密度、道路限速、公交站点密度、饱和度等主要因素，建立了启发式道路阻抗函数［26］；王元庆等在广义交通阻抗概念下，提出综合路阻函数模型。把时间、费用、交通流、收费站和城市节点影响通过参数标定建立起综合函数关系［27］；王磊针对目前公交查询系统存在的问题，利用Dijkstra算法求解公汽和地铁换乘方案的最佳路线选择［28］；童春雷就企业机器的成本相关问题，应用Dijkstra算法来求解，为企业管理者对成本的控制提供了一定的方法［29］；王海晓阐述了Dijkstra基本思路以及在选择运输最短路径中的应用，以实现物流运输路径最短、运费最低、最大限度的节约物流成本以提高产品的竞争力［30］。

1 研究的理论基础与技术方法

1.1 问题描述

应急物资的调度是应急物流研究的主要部分，其与普通物流存在着许多不同之处，最明显的区别在于普通物流主要考虑的是节省成本，而应急物流除需要考虑成本因素外，还需考虑救援的时效性。灾害发生之初，决策者若选择距离受灾点最近的供应点进行物资调度可以降低救援延迟时间，也可以减少物资运送距离，但却不一定能将整体灾害损失降到最少，也不一定能将整体救援成本降低。因为灾害损失不但与救援延迟时间有关，还与受灾程度有关，而救援成本不但与运输距离有关，还与公路路况环境有关；实际上，受灾点的受灾程度是有地域差异的，其救援紧迫性往往不一样；而各供应点到受灾点的公路路况也不尽相同。

在以降低灾害损失为决策目标的应急供应阶段中考虑灾区受损程度，以降低救援成本为决策目标的持续供应阶段中考虑公路的路况环境，是解决此应急调度问题的关键所在。

当灾害发生后，为减轻灾害造成的损失和影响，供应点需对受灾区域进行应急救援。救援过程往往不计成本，以尽可能减少灾害损失为主要决策目标。由于灾害造成的损失与受灾区域受损程度及救援延迟时间有关，同等受灾程度下，若能在灾害发生后以更快的速度投入救灾，则由灾难造成的损失将更小。由于同一种自然灾害的危害程度存在明显的地域差别，故灾害发生后，迅速对受灾各区域进行受损评估，对指导应急资源的调度具有重要意义。利用AHP决策分析法可以对各受灾区域进行受灾程度评估，以确定各受灾区域的救援急迫性，并按照评估指标的选取原则，将组成因素分为以下四类：受灾区域的人口密度（高、中、低）、经济发达程度（发达、中等、欠发达）、房屋覆盖密度（高、中等、低）、抗灾投入（多、中等、少）［31］。

在实际应用中，如发生重大灾害时，受灾群众在撤退路程中遇到的实时阻碍因素会有很多，比如人群、车辆集中拥挤到一条路线上，导致人群的密度过大，使得原本的最佳撤退路径受到阻碍；灾害导致地形变化，造成路线坍塌也会使得路线受阻。这些情况都是容易发生的，应该被综合考虑到最佳路径的选择决策中。灾害中灾区的实时路况时刻改变，因此应该采用动静结合的方式来选择最优撤退路径。静态寻优过程与灾害区内的实时交通状况无关，只与区内的交通路网情况有关，主要采用Dijkstra方法来计算。动态寻优也可称为时间最短寻优，与灾害发生点的实时交通状况存在密切的联系，主要通过路阻函数计算中的半理论、半经验方法［32］来分析计算。

1.2 路阻函数理论分析

道路阻抗函数，简称路阻函数，就是把道路阻抗定量化的数学表达式。路阻函数能够对行驶时间和交通条件（如交通速度、流量、密度等构成）以及道路条件（如道路道路宽度、道路几何形状、道路类型等方面）之间的相互关系进行综合反映。国内外有很多学者对路阻函数的模型进行了大量的研究，并提出了各种不同的函数模型，其中有一些模型在实际应用中显示出的效果比较满意。目前研究路阻函数关系的主流模型主要有两大类：一类是回归模型，常为根据实测路段行驶车速、交通负荷及几何条件等数据，然后采用最小二乘法确定的线性或非线性模型；另一类为交通流三参数模型，即根据交通流中交通量、速度及密度三者之间的交通流模型，推导出速度与交通负荷之间的关系模型，然后再通过对实际道路以及交通条件进行修正而得到的模型。

1.3 Dijkstra算法分析

Dijkstra算法是采用标号原理来实现对最短路径的搜索。Dijkstra算法采取的方法是不断地对顶点进行标号。算法开始后，每次标号一个顶点，标号的值即为从给定源点到该点的最短路径权值。首先，在所有与固定源点有边相连的顶点中找到离源点最近的顶点，递归地，设已找到当前最短路径的一部分-由与源点距离最短的n个结点和相应的n条最短路径构成，此时，这n个结点到源点的最短路径权值将会成为它们各自的永久标号。对所有没有被标记的顶点u，构成y条从源点到未标记顶点的路径，在这y条路径中选择权值最小的一条，其权值将作为顶点u的暂时标号。然后，用同样的方法可以获得其它未被标号的顶点的暂时标号，最后在所有的暂时标号中选择权值最小的一个，这个具最小标号的顶点（设为x）就是我们要找的第k＋1个顶点，将x的标号作为其永久标号，最短路径生成树生成到x。重复上述过程直到所有顶点都有了永久标号为止［33］。

2 应急决策信息系统最优路径求解的模型推理

本文主要通过路阻函数理论和Dijkstra算法两种方法的结合，从动态寻优和静态寻优两种路径选择方面来分析计算合理有效的避难最优撤退转移路径。具体方法是：采用动态寻优方法来计算实时路径权值，再根据获得的实时路径权值应用静态寻优方式最终确定最优撤退路径。

2.1 基于路阻函数理论动态寻优方式分析计算实时路径权值

动态路径分析主要计算灾民从受灾区向安置点（目的地点）行进的各条路段的路径权值。路径权值可以用通过某一路段的行驶或者迁移所花费的时间来进行表示。路阻函数是指路段行驶时间与路段上的交通负荷之间的函数关系。对于交通状况较为简单的路段而言，各路段上的路径权值（通行时间）可采用以下公式：

式中：T（通行时间）为路径权值（min）；S为路段长度（km）；路段上的行驶速度V根据道路等级的不同而采取相应等级的设计车速（km／h）。

然而，在实际灾害发生后的撤退路径中，道路上会行驶着不同的人群、车辆以及财产物资，交通状况相对较为复杂。因此，在混合交通情况较为严重的状况下，宜采用一种半理论、半经验的路阻函数求解法。这种方法的思想是：根据交通流理论中交通量Q、速度V、密度K三参数的关系来确定路阻函数的理论模型；其中Q＝KV；然后确定路权函数理论模型。路径权值的计算公式如下［34］：

式中：T（p，q）表示路段［p，q］上的行驶时间（min）；S（p，q）表示路段［p，q］的长度（km）；Vm表示路段畅通时的行驶速度（km／h）；Q（p，q）表示路段［p，q］上的交通量；Km表示路段堵塞密度。

当Q≤VmKm／8时，路段交通状况处于正常状况，根式前取“＋”号；当Q＞VmKm／8时，路段处于拥挤状态，根式前取“－”号；当Q≥VmKm／4时，此时定义为灾害发生后，道路遭到摧毁无法通行，取V（p，q）＝0。

灾害发生后，道路交通状况混乱复杂。因此需要根据实时交通状况对模型参数Vm和Km进行修正。灾害发生后，人们在紧急撤退的过程中，路段的交叉口信号灯主要依靠人为控制，因此此时不考虑在修正参数行列之内。此时参数的修正主要从两方面进行：行人干扰修正、车道宽度影响修正。计算公式如下：

式中：μ1为行人干扰修正系数；μ2为车道宽影响系数；V0为路段设计车速；n为单向机动车车道条数；L为平均车长长度；L0为平均阻塞车间净距，可取1.5 m。

灾害发生后的道路与以往大不相同，人群四处散开。行人横穿等干扰对交通状况有很大的影响。对于灾害现场道路，行人横穿流量是未知的，对修正系数μ1无法进行定量计算，只能采取定量与定性相结合的方法，根据实况道路干扰程度确定。表2所示为建议的行人干扰修正系数值。

表2 行人干扰修正系数值

车道宽度对道路交通状况也有较大的影响，一般而言在城市道路设计中，取标准车道宽度为3.5 m，当道路宽度小于该值，则认为行驶自由度会受到影响，车速、通行能力下降；当道路宽度大于该值，则认为利于行驶，车速、通行能力提高。其车道宽度影响修正系数可以由下面的公式确定：

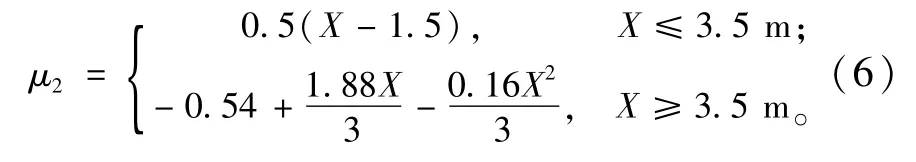
式中：X为道路宽度（m）。

2.2 基于Dijkstra算法静态寻优方式分析计算最优路径

在前面根据路阻函数理论可以计算出基于实时路况的各个路段道路权值，用路段的行驶或者迁移所消耗的时间T（p，q）进行表示。此时根据所得的路径权值，再结合Dijkstra算法进行静态寻优即可计算出最优撤退路径。

3 实例计算

图1是某受灾地区网络中的带权图，图中各个路段的路径权值均可由前面介绍的路阻函数理论计算得到。考虑到实地计算的复杂性，本文采用模拟数据。以2013年4月20日四川雅安芦山7.0级地震为例，地震发生后，人们需要撤离到安置点。假设某居民区受灾，居民区民众需要转移到安置点进行安置。芦山的主要安置点为芦山体育中心安置点、芦山中学安置点以及其他临时帐篷安置点。其中u1为受灾居民区，芦山体育中心安置点位于顶点u5、芦山中学安置点位于顶点u7、某临时帐篷安置点位于u8。

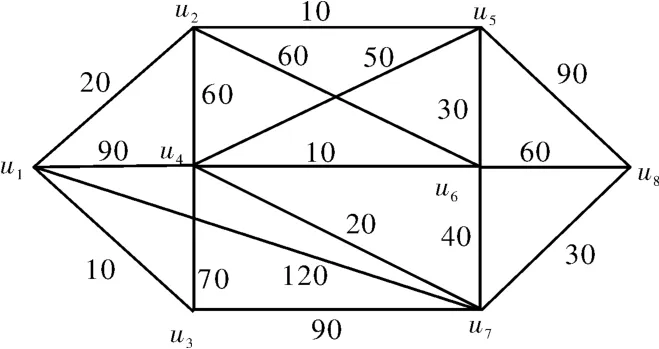
图1 受灾居民区网络带权图

现需要求出从受灾居民区u1出发分别到安置点u5、u7、u8使用时间最短的路径。

步骤1：由于是要求从u1出发到其他三个安置点的最短路径，故设u1作为源点，此时S＝｛u1｝，当前最短路径u1→u1＝0。此时其他顶点均为被标记，故定义集合U＝｛u2，u3，u4，u5，u6，u7，u8｝。以u1为中间点，从u1开始找，与u1有边相连的点有四个，分别为：u2、u4、u7、u3，此时u1→u2＝20，u1→u4＝80，u1→u7＝140，u1→u3＝10。比较容易得知u1→u3＝10的权值为最短。

步骤2：由步骤1可知u1→u3＝10的权值最短，则将u3加入集合S，此时S＝｛u1，u3｝，U＝｛u2，u4，u5，u6，u7，u8｝，当前最短路径为u1→u1＝0，u1→u3＝10，以u3作为中间点，从u1→u3＝10这条最短路开始找下一条最短路。与u3有边相连的未被标记的顶点为u4、u7。此时u1→u3→u4＝80，u1→u3→u7＝100。由于步骤1中的u1→u7＝120比u1→u3→u7＝100要长，于是将u1到u7的权值改为u1→u3→u7＝100。比较可知u1→u3→u4＝80的权值最短。

重复上述步骤，对全部顶点进行查找，最后使得集合U为空集，认为查找完毕。

根据上述算法，可以得到受灾群众从受灾居民区u1到芦山体育中心安置点u5的最优撤退路径如图2所示。

图2 受灾居民区u1到芦山体育中心安置点u5的最优撤退路径

受灾群众从受灾居民区u1到芦山中学安置点u7的最优撤退路径如图3所示。

图3 受灾居民区u1到芦山中学安置点u7的最优撤退路径

受灾群众从受灾居民区u1到某临时帐篷安置点u8最优撤退路径如图4所示。

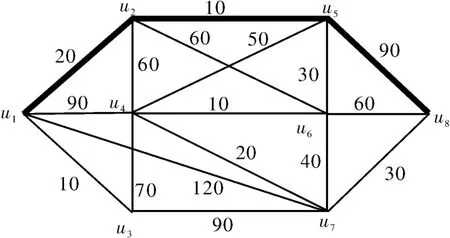
图4 受灾居民区u1到某临时帐篷安置点u8的最优撤退路径

其次，当灾害发生时，在选择正确的避灾救灾路线时，还需就具体情况具体分析。比如需要考虑到安置点的最大容纳人数，撤退总人数等等。结合实际情况进行优化改进也是应急决策信息系统的重要部分。

在选择撤退路线时，应该优先选择距离受灾点最短的路径的安置点，当安置点超出容纳人数时再选择其他的安置点。根据上一部分求出的源点到各个安置点的路径，将受灾源点到安置点的最短路径按时间长短进行降次排序，如表3所示。

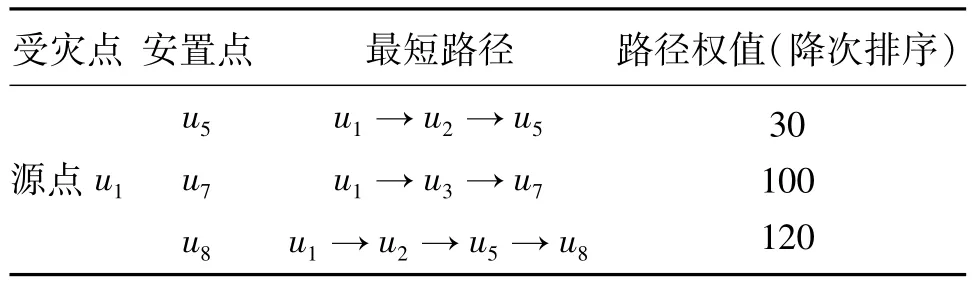
表3 受灾点到各个安置点的最短路径

假设受灾小区居民总人数为12 000人，芦山体育中心安置点u5最大可容纳5 200人，芦山中学安置点u7最大可容纳4 000人，临时帐篷安置点u8的最大容纳量为3 000人。由于容纳人数的限制，在应急决策信息系统中，需要对人群进行合理的分流安排。考虑到安置点容量的最终的受灾群众安排情况如表4所示。

表4 根据安置点容量最终选择的最优人群分流

4 结束语

当发生紧急灾害时，受灾群众应该迅速撤退到事先选定的安置点处，受灾群众在灾害后的最优撤退路径问题是应急决策信息系统研究的问题之一。本文提出了基于路阻函数理论与Dijkstra算法相结合的方法计算出更合理的灾害最优撤退路径。灾害影响范围广和破坏性极强的特性，导致灾害发生后，实时的道路交通情况与以往大不相同。根据复杂的灾害交通状况，该研究思路能有效的结合具体的灾害的实时道路环境来提供最优路径，为应急决策信息系统决策提供了现实与理论依据，将有助于推进我国应急信息管理实践、提高国家和全社会的抗风险能力、保障人民生命财产安全、促进经济社会发展和社会主义和谐社会建设。

［1］ Niehols，Jolin M.A major urban earthquake：planning for armageddon［J］.Landscape and Urban，2005，73（2／3）：136－154.

［2］ Eser Durukal.Critical evaluation of strongmotion in Kocaeli and DUzce（Turkey）earthquakes［J］.Soil Dynamics and Engineering，2002，22（7）：589－609.

［3］ Yin Zhiqian.Contentof analysing earthquake losses in city and the proeessof countermeasures deeision——making for disastermitigation［J］.Chinese Seienee Abstraets Series B，1995，14（3）：59－60.

［4］ 2000－2010中国环境统计年鉴［M］.北京：中国统计出版社，2010.

［5］ 李智，林达龙，明亮，等.灾后物资供应系统风险预警可拓模型的初步设计［J］.灾害学，2012，27（3）：137－138，144.

［6］ 刘晓岚，刘颖，迟晓明.我国灾害信息传播的研究现状与展望［J］.防灾科技学院学报，2010，12（1）：132－137.

［7］ 刘文玉，吴湘滨，安静，等.滑坡灾害危险性评价信息图谱研究——以福建省莆田市为例［J］.灾害学，2010，25（2）：21－26.

［8］ 邓忆瑞.基于场论的信息扩散研究［J］.情报杂志，2008，3（8）：47－53.

［9］ 李卫江，温家洪.基于Web文本的灾害信息挖掘研究进展［J］.灾害学，2010，25（2）：119－124.

［10］冯志波.决策支持系统与管理信息系统的比较研究［J］.科技信息，2007，2（12）：86－87.

［11］黄瑾，谢梅生，胡辉，等.快鸟图像的地质灾害遥感信息识别研究［J］.国土资源信息化，2010，11（2）：25－31.

［12］张晓刚，刘进忙，刘昌云.信息融合系统中的数据标准化研究［J］.情报指挥控制系统与仿真技术，2002，9（8）：38－42.

［13］陈晓红，刘芳.突发事件中的政府信息公布研究综述［J］.档案学研究，2011，4（5）：15－20.

［14］张永领.基于模糊聚类的应急物资分类储备研究［J］.灾害学，2012，27（1）：130－134.

［15］周玲.危机管理七法则中情报功能［J］.情报科学，2005，23（4）：597－601.

［16］Rees W E，Wackernagel M.Our ecological footprint：reducing human impact on the earth［M］.Gabriola Island，British Colombia：New Society Publishers，1996.

［17］Stefan Gossling.Ecological footprint analysis as a tool to assess tourism sustainability［J］.Ecological Economics，2002，43（2）：199－211.

［18］刘春林，何建敏，施建军.一类应急物资调度的优化模型研究［J］.中国管理科学，2001，9（3）：29－36.

［19］Equil，GalloG，Marziale S，etal.A combined transportation and scheduling problem［J］.European Joumal of Operatinal Research，1997，23（97）：94－104.

［20］Linet O zdamar，Ediz Ekinci，Beste Küc，et al.Emergency logistics planning in natural disasters［J］.Annals of Operations Research，2004，129（14）：217－245.

［21］何建敏，刘春林，尤海燕.应急系统多处救点的选择问题［J］.系统工程理论与实践，2001，21（11）：89－93.

［22］陈艳静.浅析公路运输企业成本控制［J］.现代商业，2011，4（11）：11.

［23］郭跃，朱芳，赵卫权，等.自然灾害社会易损性评价指标体系框架的构建［J］.灾害学，2010，25（4）：68－72.

［24］邵海鹏.公路网应对自然灾害系统框架研究［J］.长安大学学报：社会科学版，2009，11（4）：6－11.

［25］周继彪，陈红.道路路阻函数模型及适用性研究［J］.公路，2013，7（7）：180－184.

［26］刘宁，赵胜川.基于BPR函数的路阻函数研究［J］.武汉理工大学学报，2013，37（3）：545－548.

［27］王元庆，周伟.道路阻抗函数理论与应用研究［J］.公路交通科技，2004，21（9）：82－85.

［28］王磊.基于Dijkstra算法的多目标城市公交最优化查询的快速算法［J］.信息通信，2012，6（7）：65－67.

［29］童春雷.Dijkstra算法在企业成本控制的应用［J］.中国商贸，2012，7（23）：87－89.

［30］王海晓.Dijkstra算法在求解物流运输最短路径中的应用［J］.价值工程，2009，5（5）：82－85.

［31］李紫瑶，孔昭君，韩秋露.应急资源动员链体系——规则、内涵及衔接机制研究［J］.灾害学，2013，28（3）：147－151.

［32］王炜，张桂红.城市道路路阻函数研究［J］.重庆交通学院学报，1992，11（3）：84－92.

［33］丁威.时间延伸网络在飓风撤离系统中的应用［D］.武汉：武汉理工大学，2009.

［34］李超杰.洪灾避难迁徙决策支持系统关键技术研究与应用［D］.北京：首都师范大学，2007.

On the Optimal Path of Emergency Decision Information System——Based on Impedance Function Theory and Dijkstra Algorithm

Liu Chunnian and Deng Qingjing
（School of Information Engineering，Nanchang University，Nanchang 330031，China）

The optimal path theory and practical study on the emergency decision information systems is an important branch and key research topics in the fields of disaster emergency informational engineering.The impedance function theory and Dijkstra algorithm into the research area of emergency decision information system optimal path is a research topic with ongoing concern and significant value.It is based on the reasoning and solving of the emergency decision information system optimal path，aswell aswith the Dijkstra algorithm for the overall technical approach and the impedance function theory for the technology extraction on the path weights of real-time sections，and also with the actual needs of emergency decision related as the center，this paper explored the theoretical technical basis and problems countermeasures of the optimal routingmechanism and application of emergency decision information system and proposed a optimal pathmathematicalmodelwhich based on impedance function theory and Dijkstra algorithm and also calculated themodelwith an example to show the effectiveness of the algorithm.Under the complex traffic environment in disaster，this research idea can bemore fully and effectively combined with specific real-time road conditions to provide a retreat optimal path for affected people in disaster.

emergency decision information system；impedance function theory；Dijkstra algorithm；optimal path

TP31；X43

A

1000－811X（2014）03－0018－06

10.3969／j.issn.1000－811X.2014.03.004

刘春年，邓青菁.应急决策信息系统最优路径研究——基于路阻函数理论及Dijkstra算法［J］.灾害学，2014，29（3）：18－23.［Liu Chunnian and Deng Qingjing.On the Optimal Path of Emergency Decision Information System——Based on Impedance Function Theory and Dijkstra Algorithm［J］.Journal of Catastrophology，2014，29（3）：18－23.］*

2013－12－02 修回日期：2014－02－25

国家自然科学基金项目（71163033）；国家自然科学基金项目（71363044）；江西省自然科学基金（20114BAB201042）；江西省教育厅科学技术研究项目（GJJ13080）

刘春年（1975－），女，湖北荆州人，博士（后），教授，博士生导师，主要从事信息资源开发与管理、灾害应急信息管理教学与研究工作.E－mail：pan81706＠163.com