“焦耳定律”教材中两个公式推导的修正
2014-05-10郑青岳
郑青岳
(浙江省玉环县教育局教研室,浙江 玉环 317600)
在人教版高中物理选修3-1第2章第5节“焦耳定律”教材中,有关于电功公式和焦耳定律表达式的推导,由于这两个推导过程存在着一些缺陷,学生理解起来较为困难.本文对这两个推导过程进行简单的剖析,并提出两个公式推导教学的修正意见.
1 关于电功公式W=IUt的推导

图1
关于电功公式的推导,教材这样写道:所谓电流做功,实质上是导体中的恒定电场对自由电荷的静电力在做功.自由电荷在静电力作用下沿静电力的方向做定向移动,结果电荷的电势能减小,其他形式的能增加.
图1(原书图2.5-1)表示很小一段电路.电荷在做从左向右的定向移动,它们从这段电路的左端移到右端所用的时间记为t.根据第1节的分析,在这段时间内通过学习这段电路的电荷总量为q=It.
如果这段电路左右两端的电势差是U,在电荷q从左端移到右端的过程中,静电力做的功是W=qU.把q=It代入,得W=IUt.
对上述推导过程,学生学习时会产生许多疑惑,如
(1)为什么推导电功公式时,所取的是“很小一段电路”?
(2)针对“很小一段电路”推出的结果能适用实际(并非很小)的电路吗?
(3)在以前的学习中,我们知道公式q=It中的q是指时间t内通过“某一横截面”的电荷量,为什么这里却是指通过“这段电路”的电荷量?
(4)公式q=It中的时间t(即在某个横截面观察的时间)为什么刚好取作电荷从左端移到右端所需要的时间呢?
(5)在时间t内,该段电路的电场力不但对进入其内的电荷做功,而且也对原来在其内所有自由电荷都做功.对所有这些电荷所做的总功为什么刚好等于W=qU呢?
以上这些疑惑,作为教师想弄个清楚也比较困难.教师即使弄明白了,也很难对学生进行解析.其实,作为推导电功的公式,完全没有取“很小一段电路”的要求.作为教学,应当以最为清晰的思路和用最通俗易懂的语言,引导学生进行逻辑严谨的推导.鉴于此,我们对焦耳定律的推导方法作了如下的修正.
图1表示一段电路.电荷在做从左向右的定向移动.在时间t内,从电路左端进入的电荷量为q=It.而在这段时间内,也有相同电荷量的自由电荷从这段电路的右端穿出.这样一个过程,相当于在时间t内电场将电荷量为q=It的自由电荷,从电路的左端移到电路的右端.所以,在这个过程中,静电力对电荷做的功是W=qU.把q=It代入,得W=IUt.
经过修正的上述推导,既科学严谨,又简洁明了,充分体现了物理学的等效思想,学生极易理解和接受.
2 关于焦耳定律表达式Q=I2Rt的推导
关于焦耳定律表达式的推导,课本中写道:电流做功时,消耗的是电能.究竟电能会转化为哪种形式的能,要看电路中具有哪种类型的元件.
电流通过白炽灯、电炉等电热元件做功时,电能全部转化为导体的内能.电流在这段电路中做的功W等于这段电路发出的热量Q,即

由欧姆定律有
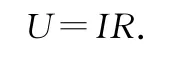
代入上式后可得热量Q的表达式为

上述推导过程中,由于针对的是电热元件(即纯电阻性元件),极容易让学生产生一种误解,即焦耳定律表达式Q=I2Rt只适用于电热元件,对非电热元件则不适用.而事实却是:焦耳定律表达式Q=I2Rt普遍适用于一切电路元件.虽然上述推导是通过特殊情形入手,得出了一般情形的结论,但在这种做法中所体现的“普遍性存在于特殊性之中”的思想,是一般高中学生难以理解的.鉴于此,我们拟对焦耳定律的推导过程进行如下修正.
(1)以纯电阻性的电热元件为对象进行推导.方法与课本中相同.
(2)以非纯电阻性的电路元件(如电动机)为对象进行推导:
①分析电路能量的转化:如图2所示,电流通过电动机时所发生的能量转化为:电能(=电功W)转化为电动机转动的动能Ek和电阻产生的内能(=热量Q).

图2

图3
②用实验方法认识电动机两端的电压与通过的电流、电动机内阻三者的关系:U≠IR,U>IR.方法如下:如图3所示,闭合开关,先使小电动机处于制动状态,读出电流表和电压表的读数I1、U2,算出电动机的电阻再让小电动机处于旋转状态,读出电流表和电压表的读数I2、U2,比较U2与I2R的关系可得U2>I2R.
根据上述两点分析可知,对非电热元件,不能采用与电热元件完全相同的方法进行推导.
③如图4所示,在思维中将实际的电动机分离成一个无电阻的理想电动机和一个电阻串联.其中M′为理想电动机,电流对它做功时,电能只转化为机械能;R为电动机的电阻,电流对它做功时,电能只转化为内能.
对于电阻R,Q=WR,UR=IR,所以可推得Q=WR=IURt=I(IR)t=I2Rt.
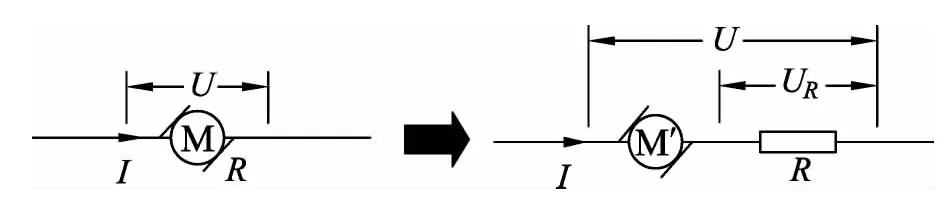
图4
可见,焦耳定律无论是对纯电阻性元件,还是非纯电阻性元件,都是普遍适用的.
