基于各向异性插值的全景图像径向展开算法

陶宏江，金龙旭

（中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033）

1 引 言

折反射全景成像设备采用摄像机正上方放置折反射全景镜头达到扩大视野的目的，具有大视场、结构简单、光能损失低、系统设计柔性好、无需运动部件扫描和搜索就可以实现实时360°成像等优点［1］。全景成像系统以及接近一个球面的全景视场信息观察能力，在军事和民用领域的应用前景都十分广阔，目前已经在机器人导航、视频会议、视频监控、虚拟现实等众多领域得到广泛应用［2］。

然而，全景成像系统通过摄像机获取的是圆形全景图像，不符合人的视觉习惯，所以还需要对全景图像进行展开，变成适合观察分析的柱面全景图像。

现在常用的展开算法依据场景中的物点坐标与成像平面内像点坐标映射关系实现图像在展开［3］，但是由于展开的柱面图像与全景图像的像素点并不是一一对应关系，存在欠采样现象，所以会产生图像块效应，降低展开图像的图像质量。本文分析了坐标映射展开法影响柱面图像质量的原因，提出了结合各向异性插值的全景图像径向展开方法，该算法能够有效的抑制块效应、提高展开图像质量。

2 基于坐标映射的柱面展开算法

2.1 坐标映射柱面展开算法的实现

基于坐标映射的柱面展开算法［4］的思想是，利用柱面展开图中直角坐标和圆环状全景图极坐标之间的坐标变换，构建柱面图中像素到圆环状全景图中像素的映射，再通过像素的填充完成柱面展开图［5－6］，如图1所示。

图1 全景图像展开示意图Fig.1 Schematic forunwrapping panoramic images

图1中，r表示圆环全景图的内径，R表示外径，在外径和内径之间的区域为有效像素区。在图像展开时，对于展开后柱状图中的任意一点A′（x′，y′），对应圆环全景图中的点A（x，y），两点间坐标关系可表示为

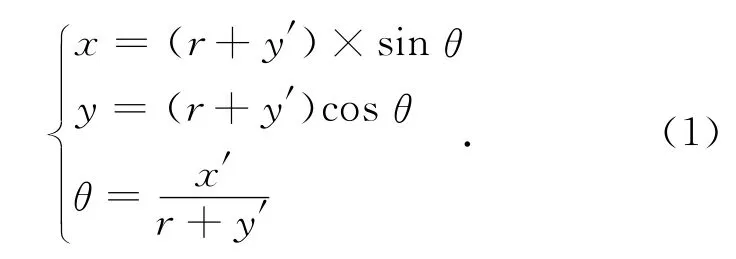
通过对柱面图中每一点进行像素替换即可得到展开图像。

2.2 坐标映射柱面展开算法的不足

由于计算机系统是一个离散的数字系统，这就导致了式（1）中的映射不是一个一对一的映射关系，即存在全景图像中的一点对应柱面图中多个点的情况。

不失一般性，假定图像传感器是正方式像素的阵列，全景相机成像时的示意图如图2所示。

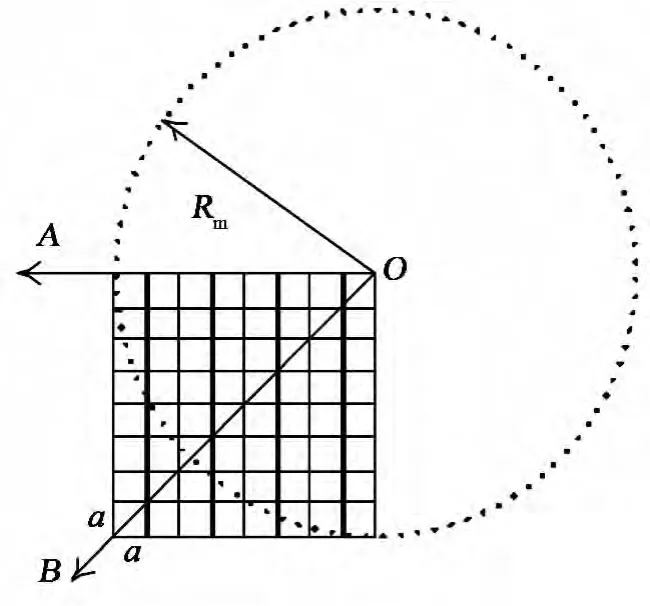
图2 全景相机成像示意图Fig.2 Panoramic camera imaging

图2中a表示传感器一个像素单元的长度，Rm表示以o为原点的全景镜头光斑的半径，可知沿A方向的传感器感光像素数为个，而在B方向的传感器感光像素数约为个，以为半径的柱面展开图有效像素近似分布如图3所示［4］。

图3 柱面展开图有效像素近似分布Fig.3 Approximate distribution of the effective pixels of cylinder figure

通过分析可得出结论，在全景图像的水平和垂直方向，柱面展开图和全景图像有一对一的映射关系，而在全景图像的其他方向，展开图像都有像素重复映射的情况，当方向角为π／2的整数倍时，像素重复映射最为严重，像素重复映射数近似为柱面展开图中一列像素数的30%。

过多的像素重复映射是导致柱面展开图像产生块效应从而导致图像质量下降的主要原因，而坐标映射柱面展开算法很难解决这一问题，因为它难以定位哪些像素是进行了多次映射的，针对这一问题，本文提出了全景图像径向展开算法。

3 全景图像径向展开算法

3.1 算法描述

全景图像的径向展开算法是基于数字图像传感器图像采集原理和计算机图形学算法的全景图像展开方法，它的展开过程如图4所示。

图4 径向展开过程Fig.4 Process of radial expanding

R是全景图像外环半径，r是全景图像内环半径，点A为全景图像外环上的展开起点，B为全景图像内环上的展开终点，A′为柱面展开图中点A的对应点，B′为柱面展开图中点B的对应点，线段A－B全景图像自A 点起到B点结束的一条像素线段，线段A′－B′表示柱面展开图中以A′点为基准的一列像素，径向展开算法过程如下：

（1）首先使用Bresenham画圆算法确定全景图像外环在图像中的像素位置，因为全景镜头和传感器之间不会移动位置，所以这一过程只需要执行一遍；

（2）选择展开的起点，本文选择圆心位置正上方圆环外径上的点，从起点开始，按顺序以圆环外径上的点执行步骤3中的直线扫描；

（3）从圆环外径上的点开始，使用Bresenham直线算法沿半径向圆心方向画直线直到圆环内径为止，把全景图像中这条径向上的点按顺序对应到柱面如图4中全景图中的线段A－B对应到柱面展开图中的A′－B′。

在仅使用Bresenham直线算法在全景图像选择线段复制到柱面展开图中时，同样会产生如图3的像素缺失现象，本文使用基于Bresenham直线算法的线段拉伸算法以保证柱面展开图中每一列具有同样的像素数。

3.2 基于Bresenham直线算法的线段拉伸

Bresenham直线算法是计算机图形学领域中使用最广泛的直线扫描转换算法，其具有只使用整数运算、只做加减法和乘2运算，实现方便，执行效率高的特点。

以第一象限为例，Bresenham直线算法以判断误差项d2－d1的符号来决定下一像素的取向，如图5所示，当d2－d1＞0时，选择右上方的点，否则选择右侧的点。

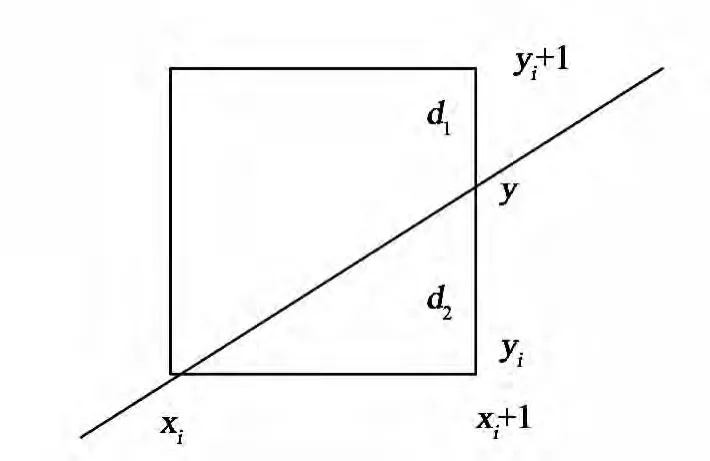
图5 Bresenham直线算法简述Fig.5 Bresenham straight－line algorithm outlined

结合图2和图3，可以得出结论：图4中线段A－B拉伸所需要插入的像素个数与Bresenham直线算法向右上方选择的次数有关，当直线每向右上方移动一点，就累积了槡2－1个像素的差异。

全景图像的线段拉伸实现就是基于这一原理，以第一象限为例，算法过程如下：

（1）以Bresenham直线算法从全景图像外环上的点向圆心画直线，直到内环结束，计算直线上点的个数与全景图像水平方向上R－r的差，即为图像展开时需要插入的点的个数；

（2）重新执行Bresenham直线算法，在扫描过程中，当直线向右上方选择时，对像素累积差异det加上槡2－1，如果直线向右选择保持det不变；

（3）当累积像素差异det大于等于1时，如果已插入像素数大于等于第一步中计算出的总需要插入像素数，则不插入插值重构像素，否则即在柱面展开图中对应位置增加一插值重构像素，同时det减1。

3.3 全景图像的插值算法

全景图像展开需要插入大量的插值像素，插入像素比例见图3，像素插值的质量对柱面展开图的视觉效果具有很大的影响，获得高质量像素结果的主要手段就是滤除因图像展开所带来的图像噪声［6－8］，本文通过对全景图像成像过程的分析，给出了基于各向异性插值［9－10］的全景图像展开插值算法［11］，全景图像成像过程如图6所示。

图6 全景图像成像过程Fig.6 Panorama image imaging process

上图中圆柱为全景镜头的成像面，全景图像的柱面展开也就是对全景镜头柱状成像面数字化重构［6］，在柱状成像面上有一待成像矩形区域AB－C－D，光线经过全景镜头双曲面折射后再经过两次反射在焦面上成像，成像面上的矩形A－B－CD 在焦面上成像为一段圆环A′－B′－C′－D′，成像面到焦面的平面映射示意图如图7所示。

图7 成像面到焦面的平面映射示意图Fig.7 Mapping schematic diagram of the image plane to the focal plane

通过上述分析可知，要在全景图像的柱面展开图中插值等效于在成像面中插值，也就是说成像面到焦面的映射等效于全景图像的柱面展开到全景图像的映射。

以焦面上全景图像外圆环正上方点对应成像面的原点，成像面到焦面的映射关系为，成像面的x轴相当于焦面上全景图像的外圆环方向，成像面的y轴相当于焦面上全景图像的指向圆心的半径。以第一象限为例，成像面上任一点M（mx，my），其在焦面极坐标上的位置为：

转换为焦面直角坐标系中为：

得出像素对应关系后，选择高斯滤波器作为成像面上的插值滤波器［7］，滤波系数为：

其中：M 为待插值点，坐标位置（mx，my），将以点M为中心的坐标系数矩阵通过成像面到焦面的映射关系映射到焦面上，这一映射过程是一个多对一的映射，焦面上映射后一个点上的滤波系数值是映射到这一点的所有成像面点的滤波系数值的和，构成由像面中极坐标位置决定的各方向系数不同的滤波数组［12］，最后通过映射后的各向异性滤波数组对待插值点进行求解得到插值结果。

4 实验结果与讨论

实验系统使用2 048pixel×1 536pixel的CMOS传感器作为图像输入源，使用本文算法对输入图像进行展开，输入图像和展开结果如图8所示，展开图像以输入图像正上方位置为起点，沿逆时针方向展开。由图中可以看到在π／2的整数倍角度位置，图像块效应得到了改善，图像质量得到了提高。本文算法和坐标映射展开算法的局部细节图如图9，相对坐标映射展开算法，本文算法结果在反光处集中度变高了，图像质量获得了改善。

图8 实验测试图像和结果Fig.8 Image and result of experimental test

图9 展开图像细节Fig.9 Comparison of expanded image

对图像的数值比较方法有很多种［13－16］，本文采用信息熵和平均梯度的方法比较图像质量，如表1所示，结果表明本文算法除运行时间略低于坐标映射展开算法，在展开图像包含的信息量和展开图像边缘轮廓清晰度方面都优于坐标映射展开算法。

表1 实验数据对比结果Tab.1 Comparison of experimental data

5 结 论

针对现有全景图像展开算法适应性差，改进困难的矛盾，根据全景图像成像原理结合计算机图形学方法，提出了基于各向异性插值的全景图形径向展开算法。该算法具有灵活性强、实现简单和执行效率较高等特点，实验表明，该算法能够改善全景图像展开导致的块效应，提高图像质量。

［1］ 曾吉勇，苏显渝.折反射全景成像系统［J］.激光杂志，2004，25（6）：62－64.Zeng J Y，Su X Y.Catadioptric omnidirectional imaging system ［J］.Laser Journal，2004，25（6）：62－64.（in Chinese）

［2］ 原新，王亮，朱齐丹.基于全向视觉传感器的图像解算方法研究［J］.哈尔滨工业大学学报，2006，38（12）：2158－2161.Yuan X，Wang L，Zhu Q D.Image calculation research based on omni－directional camera［J］.Journal of Harbin Institute of technology，2006，38（12）：2158－2161.（in Chinese）

［3］ 陈旺，徐玮，熊志辉，等.折反射全向图像柱面展开校正算法研究［J］.中国图像图形学报，2009，14（12）：2559－2565.Chen W，Xu W，Xiong Z H，et al.Rectification of catadioptric omnidirectional images via cylindrical unwarping［J］.Journal of Image and Graphics，2009，14（12）：2559－2565.（in Chinese）

［4］ 田晓东.折反射全景成像系统分析与设计［J］.仪表技术与传感器，2006（4）：48－50.Tian X D.Analysis and design of catadioptric panorama image system ［J］.Instrument Technique and Sensor，2006（4）：48－50.（in Chinese）

［5］ 何四华，邵晓方，杨绍清，等.双曲面折反射全景成像柱面展开图像质量分析［J］.激光与红外，2012，42（2）：187－191.He S H，Shao X F，Yang S Q，et al.Analysis for the cylinder image quality of hyperbolic－catadioptric panorama image system ［J］.Laser ＆Infrared，2012，42（2）：187－191.（in Chinese）

［6］ 任文琦，王元全.基于梯度矢量卷积场的四阶各向异性扩散及图像去噪［J］.光学精密工程，2013，21（10）：2713－2719.Ren W Q，Wang Y Q.GVC－based fourth－order anisotropic diffusion for image denoising［J］.Optics and Precision Engineering，2013，21（10）：2713－2719.（in Chinese）

［7］ Aubert G，Kornprobst P.Mathematical Problems in Image Processing：Partial Differential Equations and the Calculus of Variations ［M］.New York：Springer，2006.

［8］ 陈仁喜，李鑫慧.基于各向异性插值模型的快速图像修复方法［J］.计算机应用研究，2009，26（4）：1554－1556.Chen R X，Li X H.Fast image inpainting algorithm based on anisotropic interpolation model［J］.Application Research of Computers，2009，26（4）：1554－1556.（in Chinese）

［9］ 苗慧，宋光磊，张春红，等.一种自适应各向异性的SAR图像去噪算法［J］.遥测遥控，2011，32（1）：28－32.Miao H，Song G L，Zhang C H，et al.An adaptive anisotropic algorithm on SAR image denoising ［J］.Journal of Telemetry，Tracking and Command，2011，32（1）：28－32.（in Chinese）

［10］ 赵建.分数阶微分在图像纹理增强中的应用［J］.液晶与显示，2012，27（1）：121－124.Zhao J.Fractional differential and its application in image texture enhancement［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（1）：121－124.（in Chinese）

［11］ Groenewald A M，Arbard E，Otha E C.Related approaches to gradient－based thresholding［J］.Pattern Recognition Lett.，1993，14（7）：567－572.

［12］ Miller K S，Ross B.An Introduction to the Fractional Calculus and Fractional Differential Equations ［M］.USA：John Wiley ＆ Sons，1993.

［13］ 李艳，苏萍，马建设.立体投影质量的评价方法及系统［J］.液晶与显示，2012，27（1）：31－37.Li Y，SU P，Ma J S.Evaluation method and system of stereoscopic projection quality ［J］.Chinese Journal of Liquid Crystals and Displays，2012，27（1）：31－37.（in Chinese）

［14］ 范媛媛，沈湘衡，桑英军.基于对比度敏感度的无参考图像清晰度评价［J］.光学精密工程，2011，19（10）：2485－2493.Fan Y Y，Shen X H，Sang Y J.No reference image sharpness assessment based on contrast sensitivity［J］.Optics and Precision Engineering，2011，19（10）：2485－2493.（in Chinese）

［15］ 刘希佳，陈宇，王文生，等.小目标识别的小波阈值去噪方法［J］.中国光学，2012，5（3）：248－256.Liu X J，Chen Y，Wang W S，et al.De－noising algorithm of wavelet threshold for small target detection［J］.Chinese Optics，2012，5（3）：248－256.（in Chinese）

［16］ 阎雪飞，许廷发，白廷柱.改进的固定点图像复原算法［J］.中国光学，2013，6（3）：318－324.Yan X F，Xu T F，Bai T Z.Improved fixed point method for image restoration［J］.Chinese Optics，2013，6（3）：318－324.（in Chinese）