一致光滑Banach空间中m-增生算子零点的粘滞迭代逼近算法

张瑜龙，张 芳

（天津工业大学理学院，天津 300160）

一致光滑Banach空间中m-增生算子零点的粘滞迭代逼近算法

张瑜龙，张 芳

（天津工业大学理学院，天津 300160）

研究了在一致光滑Banach空间中m-增生算子的零点粘滞迭代逼近问题，证明了修正的迭代序列强收敛到m-增生算子的一个零点，此结果推广和改进了一些作者的相关结论.

m-增生算子；不动点；一致光滑Banach空间

增生算子是最重要的几类非线性算子之一，关于增生算子的零点问题已经获得了丰富的结果[1-2].近几十年来，国内外数学家们一直致力于寻找迭代算法以逼近增生算子的零点，这类问题已经成为非线性泛函分析研究中的热点问题之一.1974年Bruch[3]使用正则化迭代算法证明了Hilbert空间中极大单调算子零点的强收敛性定理；1979年Reich[4]将Bruch的主要定理结果扩展到了一致光滑的Banach空间中的m-增生算子的零点问题；2006年Xu[5]用迭代序列xn+1=αnu+（1-αn）Jrnxn去逼近m-增生算子的零点，并证明了该序列强收敛到m-增生算子的一个零点.本文受Xu研究方法的启发，在一致光滑的Banach空间中，修正了Xu的迭代序列，并证明了修正后的迭代算法的强收敛性，此结果推广和改进了一些作者的相关结论[6].

1 预备知识

设（X，d）为度量空间，称T：（X，d）→（X，d）是一个压缩映射，如果存在0＜α＜1，使得：

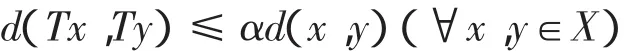
设（X，d）为度量空间，称T：（X，d）→（X，d）是非扩张的，如果∀x，y∈X，则

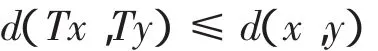
设E是一个具有范数‖·‖的实Banach空间，其对偶空间为E*，C是E的一个非空闭凸子集，＜·，·＞表示E与E*间的配对，正规对偶映射J：E→2E，定义如下

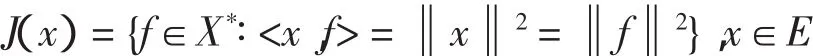
众所周知，E是光滑的当且仅当J是单值的.

设S={x∈E:‖x‖ =1}表示实Banach空间E的单位球，E是光滑的如果下面极限

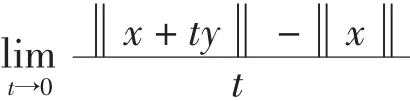
对每一个x，y∈S存在，如果每一个y∈S对任何x∈S上面的极限一致被得到，则E是一致光滑的.众所周知，如果E是一致光滑的，则正规对偶映象J是单值的，而且在E的任一有界子集上是一致连续的.

Banach空间E中具有定义域D（A）和值域R（A）的算子A:D（A）⊂E→E称为增生的，如果对任意的x，y∈D（A），存在j（x，y）∈J（x，y），使

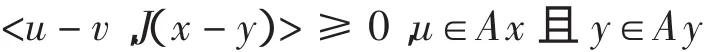
称增生算子A为m-增生的，如果存在某个正数使得I+rA的值域是全空间，即

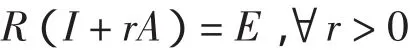
对于 m-增生算子A，r＞ 0，令Jr=（I+rA）-1，则Jr称为A的预解算子.F（J）r是Jr的不动点集.以下用F表示算子A的零点集，即F=A-（10）={x∈D（A）:0∈Ax}.众所周知，如果A是m-增生的，那么其预解算子Jr是非扩张的且对于所有的r＞0，有F（J）r=F.在本文中总假定A是m-增生的且零点集非空.

引理1[7-8]（预解等式）设E是Banach空间，对任意的λ＞0，μ＞0有以下等式成立

引理2[9-10]设{αn}是一个非负实数列满足下面性质：αn+1≤（1-λn）αn+λnμn，n≥0，其中λn｛⊂（0，1）并且μn｛｝使得

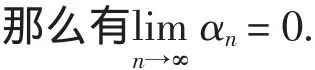
引理3[11]设C是一致光滑的Banach空间E的非空闭凸子集，设T:C→C是具有不动点的非扩张映象且F（T） ≠，并且f是C→C的一个具有常数α（0＜ α ＜1）的压缩映射，定义zt=t（fz）t+（1-t）Tzt，t∈（0，1），序列{zt}强收敛到一个点p∈F（T）.

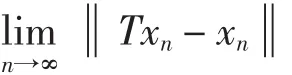
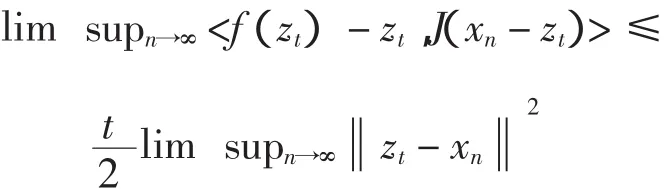
引理5[12]若E是Banach空间，对任意x，y∈E，那么以下式子成立

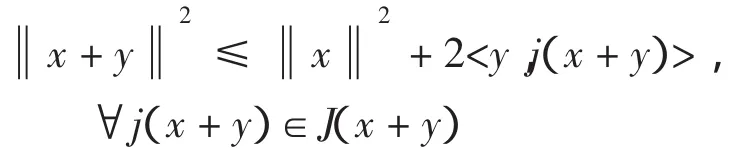
2 主要结果

定理1 设E是一致光滑Banach空间，A是E中的m-增生算子使得C=是凸的，f是C→C的一个具有常数α（0＜α＜1）的压缩映射.给定序列，βn｛｝∈[0，1]及rn｛｝，序列xn｛｝定义如下

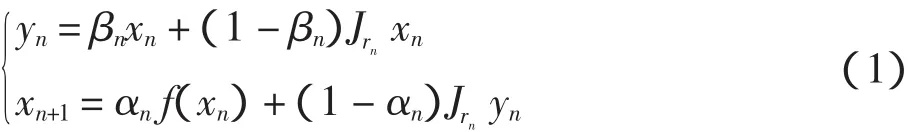
如果序列｛αn，｛βn和｛rn｝满足如下条件=r，rn≥ε，其中 ε＞ 0.则由式（1）定义的迭代序列xn｛｝强收敛到A的一个零点.

证明首先证明序列xn｛｝是有界的.事实上，对任意的v∈F=A-1（0），有

（iii）由归纳法可知

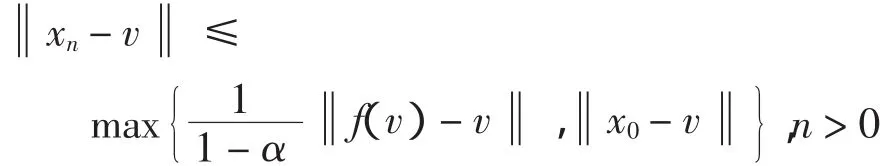
即序列xn｛｝有界，那么序列yn｛｝也是有界的.

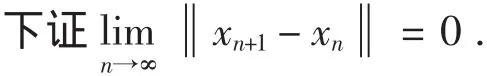
证明：由引理1知

如果rn-1≤rn则

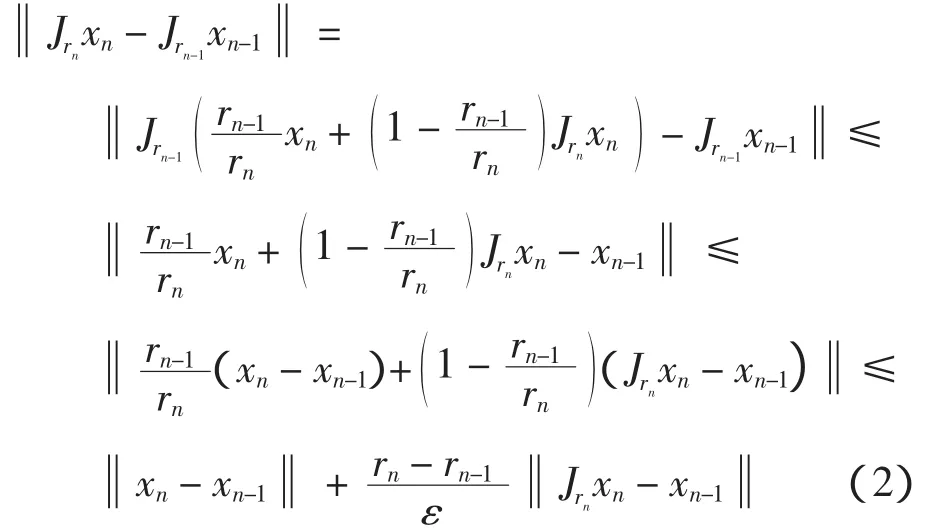
同理可证

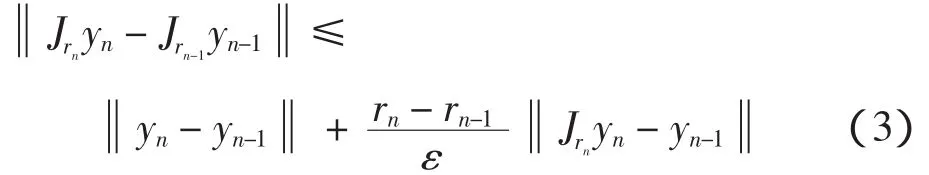
由定义并结合式（2），可得

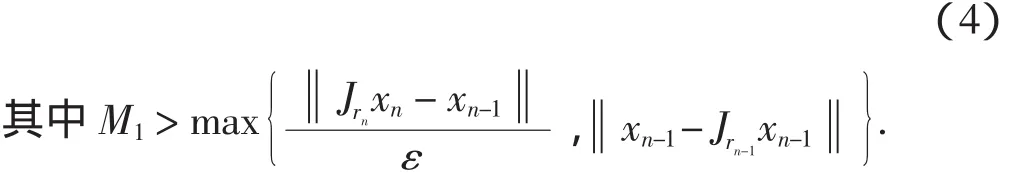
再由定义并结合式（3）和式（4）可得

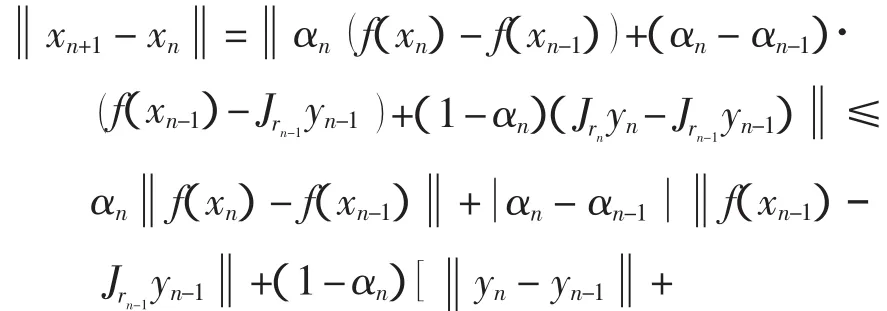
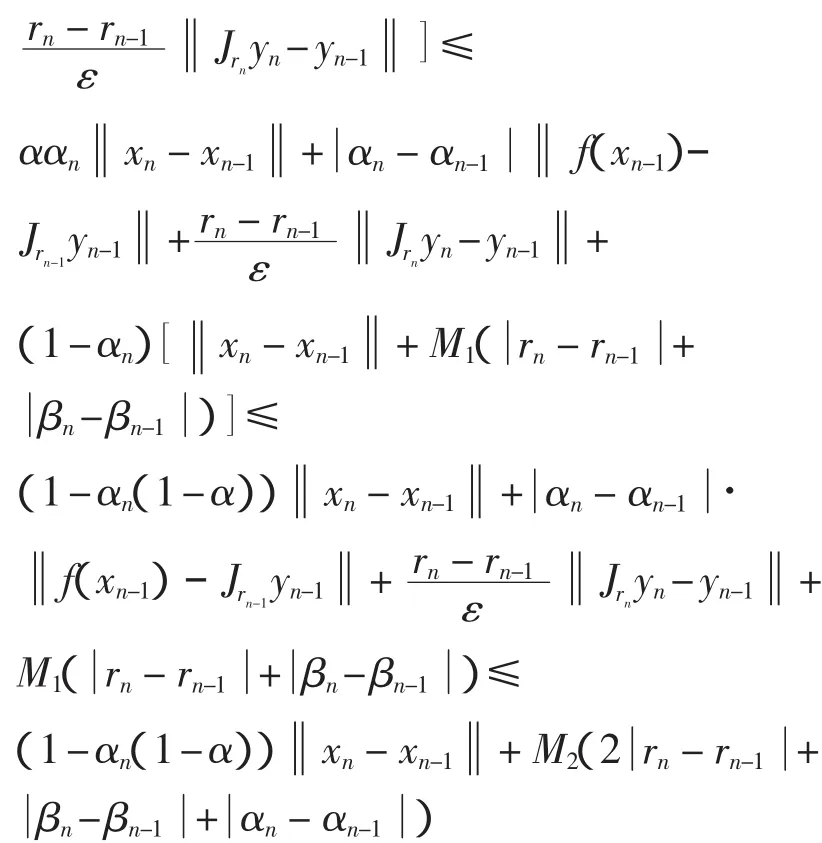
其中M2是某一常数，满足

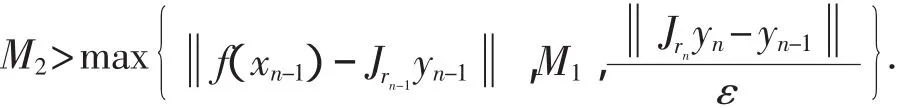
当rn-1≥rn，同样可以证明上面的结论，由定理条件可得

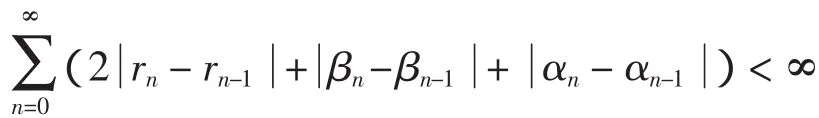
成立.

由引理2得

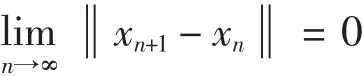
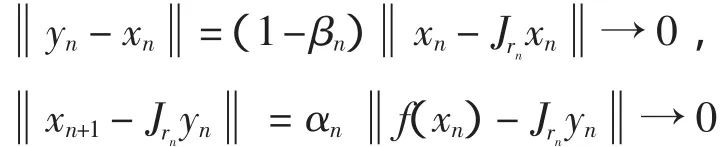
从而有

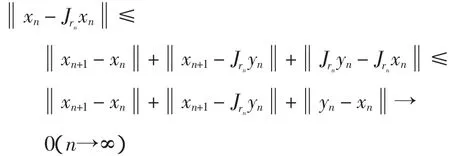
又因为

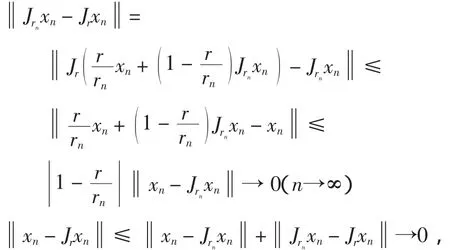
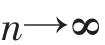
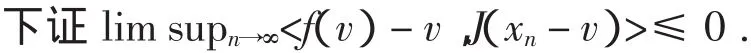
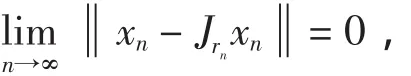
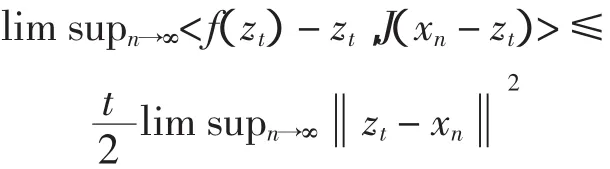
对所有的t∈（0，1），有

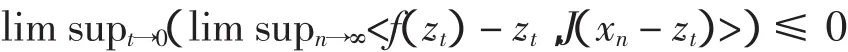
由于E是一致光滑的Banach空间，J在C上的有界子集是范数对范数一致连续的，由同样的讨论证明[10]，可得到

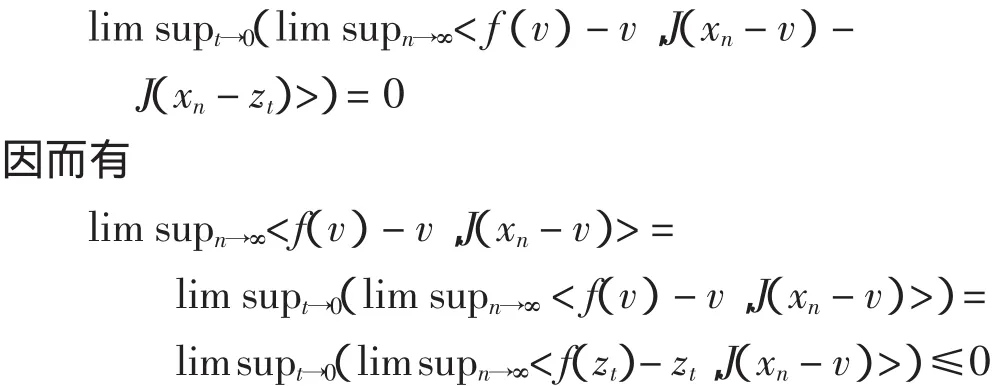
最后证明xn→v，由引理2，有

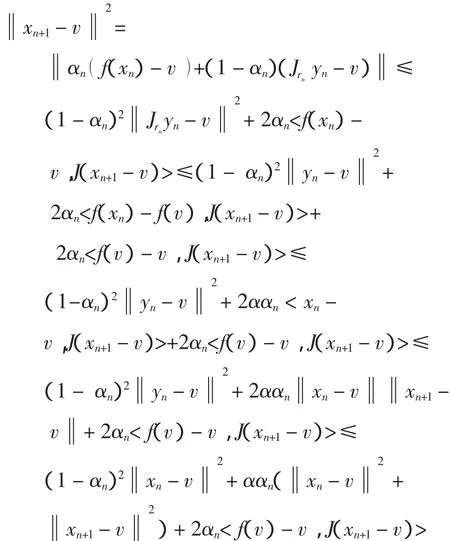
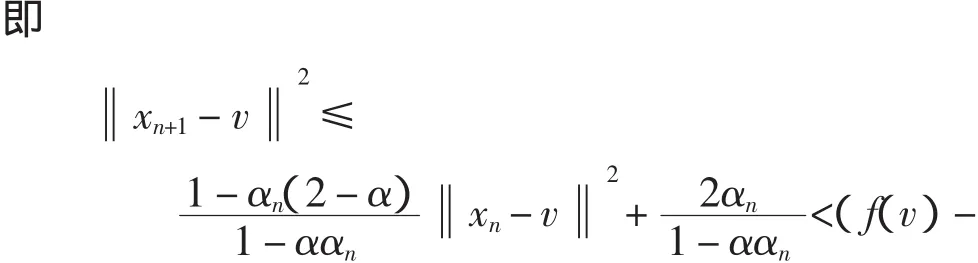
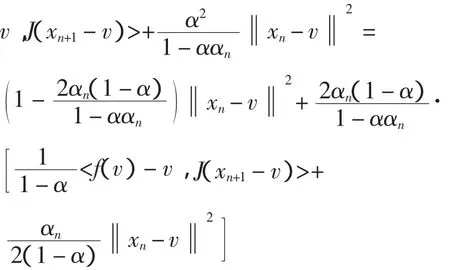
设M=max｛‖xn-v‖2｝，则上式为

定理2 设E是一致光滑Banach空间，A是E中的m-增生算子使得C=是凸的.给定序列，βn｛｝∈[0，1]及rn｛｝，序列xn｛｝定义如下

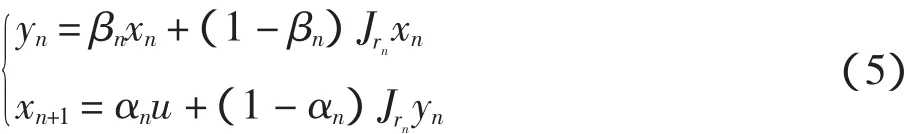
如果序列｛αn，｛βn和｛rn｝满足如下条件

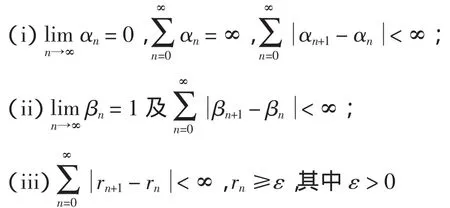
则由式（5）定义的迭代序列xn｛｝强收敛到A的一个零点.

证明令定理1中的f（xn）=u，证明方法如上面所证，则迭代序列xn｛｝强收敛到增生算子A的一个零点.

3 结束语

本文主要在文献[5]、[10]结论的基础上采用新的方法由一步迭代推广到两步，并且使用粘滞迭代算法证明了迭代序列（1）式强收敛到增生算子的一个零点，此结果改进和扩展了文献[5]、[10]的结果.

[1]DEIMLING K.Zems of accretive operator[J].Manuscrlpta Math，1974，13：283-288.

[2]BROWDER F E，PETRYSHN W V.Construction of fixed points of nonlinear mapping in hibert spaces[J].J Math Anal Appl，1967，20：197-200.

[3]BRUCH R E.A strong convergent iterative solution for a maximal monotone operator in hiben spaces[J].J Math Anal Appl，1974，48：114-126.

[4]REICH S.Constructing zeros of accretive operator[J].Applic Anal，1979，9：159-163.

[5]XU H K.Strong convergence of an iterative method for nonexpansive and accretive operators [J].J Math Anal Appl，2006，314：631-643.

[6]XU H K.Iterative algorithms for nonlinear operators[J].J London Math Soc，2002，66：240-256.

[7]BRUCK R E，PASSTY G B.Almost convergence of the innite product of resolvents in Banach spaces[J].Nonlinear Anal，1979（3）：279-282.

[8]BRUCK R E，REICH S.Nonexpansive projections and resolvents in Banach spaces[J].Houston J Math，1977（3）：459-470.

[9]XU H K.An iterative approach to quadratic optimization[J].J Optim Theory Appl，2003，116：659-678.

[10]REICH S.Strong convergence theorems for resolvents of accretive operators in Banach spaces[J].J Math Anal Appl，1980，75：287-292.

[11]SOMYOT Plubtieng，RATTANAPORN Wangkeeree.Strong convergence of mann iterations for a countable family of nonexpansive mappings[J].Nonlinear Anal，2009，70：3110-3118.

[12]CHO Yeol Je，KANG Shin Min，QIN Xiaolong.Approximation of common xed points of an innite family of nonexpansive mappings in Banach spaces[J].Computers and Mathematics with Applications，2008，56：2058-2064.

Iterative method approximating zero points of m-accretive operators in uniformly smooth Banach spaces

ZHANG Yu-long，ZHANG Fang
（School of Science，Tianjin Polytechnic University，Tianjin 300387，China）

The iterative method approximating zero points of m-accretive operators in uniformly smooth Banach spaces is studied.The strong convergence to a zero of the modified iterative sequence is proved.These results extend and improve corresponding results of others.

m-accretive operator；fixed points；uniformly smooth Banach space

O177.2

A

1671-024X（2014）02-0081-04

2013-10-22 基金项目：国家自然科学基金资助项目（11071279）

张瑜龙（1987—），男，硕士研究生.

张 芳（1974—），女，博士，副教授，硕士生导师.E-mail：zhangfangsx@163.com