基于遗传算法求解NPC问题的研究
2014-05-08宋建民贺毅朝
王 勋,宋建民,贺毅朝
(1.石家庄经济学院 信息工程学院,河北 石家庄 050031;2.石家庄经济学院 数理学院,河北 石家庄 050031)
NP完全问题(NP-Complete problem,NPC)[1,5]是理论计算机科学中非常重要的一类难解问题,对于计算复杂性的研究起着关键的作用。0-1背包问题(0-1Knapsack problem,0-1KP)[2,5]和SAT 问题(Satisfiability problem,SAT)[3,5,12]均为 NPC中非常经典的问题,同时也是组合优化问题[11,13],其中KP在预算控制和货物装载等领域有广泛的应用,而SAT问题在逻辑推理和人工智能等领域有广泛的应用。笔者利用遗传算法与某些策略相结合求解0-1KP和SAT问题,并且通过具体的实例计算验证了其可行性和有效性。
1 遗传算法简介
遗传算法(Genetic algorithm,GA)[4]是1975年由美国密西根大学的D.J.Holland借鉴生物进化机制提出来的一种仿生算法。在GA中,将待求解问题的每一个可行解看作是群体中的一个染色体个体,利用二进制(或十进制)编码表示,其优劣由适应度来衡量(适应度不一定是目标函数值)。在GA的进化中,利用交叉算子和变异算子作用于当前群体中的个体而产生新的个体,根据新个体的适应度由选择算子选择来构成新一代种群,如此反复迭代进化,直到获得满意的结果为止。GA的算法流程一般描述如下:
算法1 GA算法
(1)初始化:设置迭代次数N,随机生成M个个体构成初始种群P(0),令进化代数t=0;
(2)计算适应度:计算种群P(t)中每个个体的适应度,确定当前最优个体B;
(3)选择操作:根据种群个体的适应度的值,利用选择算子从第t代群体P(t)中选出M个优良个体(可能出现某个体被选择多次的情况)遗传到下一代群体P1中;
(4)交叉操作:对群体P1中M个个体以交叉概率(crossover rate)Pc进行交叉操作,生成群体P2;
(5)变异操作:对群体P2中每个个体以变异概率(mutation rate)Pm进行变异操作,产生第t+1代群体P(t+1),并令t=t+1;
(6)终止条件判断:判断是否满足终止条件,若满足则输出B和f(B)并结束,否则转至(2)继续迭代进化。
由于选择操作、交叉操作、变异操作和适应度计算等的时间复杂度均是关于问题维数的多项式,而遗传算法的迭代次数通常也是关于问题维数的多项式,因此GA是一个复杂度为多项式时间的随机算法。
2 0-1KP和SAT问题的数学模型
2.1 0-1KP的数学模型
0-1背包问题(0-1Knapsack Problem,0-1KP)[2,7]是一种典型的 KP问题,其本质是在资源有限的条件下追求最大收益的资源有效分配问题,它的一般描述如下:
令wi和pi分别表示n个给定物品中的第i(1≤i≤n)个物品的重量和价值,C表示背包的容量,其中wi,pi和C都是正整数,如何从这n个物品中选择物品装入背包使在不超过背包容量C的前提下其价值之和达到最大?
0-1KP问题存在许多数学模型,其中最常实用的模型如下:

xi为0-1决策变量,当xi=1时表示将物品装入背包中,当xi=0时则表示不将其装入背包中。显然0-1KP问题是一个约束最优化问题,(2)式为其约束条件。
2.2 3-SAT问题的数学模型
SAT问题[6,12]是Cook证明的第一个NPC问题[5]。目前,求解SAT问题已经有多种算法,如DP算法、局部搜索算法、模拟退火算法和近似算法等[6]。由于3-SAT问题是一类特殊的SAT问题,因此SAT问题的数学模型对于3-SAT问题也是适用的。
令Pi是变元集合{q1,q2,…,qm}中变元qi(1≤i≤m)的正文字或负文字,则形如C=P1∨P2∨…∨Ps(1≤s≤m)的命题形式称为子句,公式A=C1∧C2∧…∧Cn称为合取范式。所谓SAT问题是指:给定命题变元集M上的一个合取范式A,称判断A是否为可满足的问题为SAT问题,即判断是否存在一个指派t=(t1,t2,…,tm)使得t(A)=1。
下面,将SAT的数学模型建立为{0,1}m上判定多项式f(x1,x2,…,xm)是否存在最小值0的数值优化问题[3]。注意到{0,1}m上的多项式f(x1,x2,…,xs)=(1-x1)(1-x2)…
jjjjjj(1-xjk)xj(k+1)xj(k+2)…xjs在 X=(t1,t2,…,tm)∈{0,1}m时的值为0当且仅当子句 Cj=在指派t=(t1,t2,…,tm)下的值为1,其中1≤s≤m,1≤j≤n,因此合取范式A=C1∧C2∧…∧Cn是可满足的当且仅当多项式函数
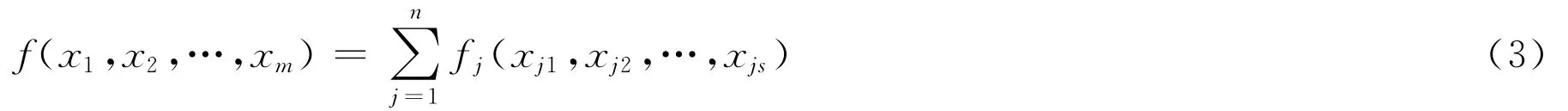
在{0,1}m上存在最小值0。由此,即建立了SAT的数学模型。
由于任意SAT问题等值于一个3-SAT问题,因此下面将主要讨论3-SAT问题的求解。
3 利用GA求解0-1KP和SAT问题
在本节中,将分别基于GA与贪心策略相结合、与局部搜索算法相结合给出求解0-1KP和3-SAT问题的改进算法GA1和GA2。
3.1 利用GA求解0-1KP问题
在利用GA求解0-1KP时,产生的新个体有可能不满足约束条件(2),称这种个体为非正常个体。非正常个体的存在将大大降低算法的收敛性,为了避免这种现象,将利用算法2给出的贪心策略[2,5,10]对非正常个体进行处理,使之成为满足约束条件(2)的个体。为了区别于基本GA,下面将结合了算法2的GA记为GA1。
令数组W[1…n]存放n个物品的重量,数组P[1…n]存放n个物品的价值,背包容量记为C,设个体X=(x1,x2,…,xn)∈{0,1}n对应的f(X)>C,即个体X 是一个非正常个体,则修正个体X的贪心策略由算法2给出。
算法2 Greedy(X)
(1)按照P[i]/W[i](1≤i≤n)由大到小的顺序对物品排序,并按所排顺序将物品下标存入数组H[1…n];
(2)令sum=0;i=1;
(3)当(sum<C且i≤n)时重复执行(4)-(6)
(4)如果XH[i]=1且sum+W[H[i]]≤C则sum=sum+ W[H[i]]且i=i+1;
(5)如果XH[i]=0则i=i+1;
(6)如果XH[i]=1且sum+W[H[i]]>C则令XH[i]=0且i=i+1;
(7)当i≤n时重复执行(8)-(9)
(8)如果sum+W[H[i]]≤C则sum=sum+W[H[i]]且令XH[i]=1,i=i+1;
(9)如果sum+W[H[i]]>C则令XH[i]=0,i=i+1;
(10)输出X,算法结束。
在算法2中,对n个物品按照价值容量比进行排序所耗费的时间最多,因此算法Greedy(X)的时间复杂度为O(nlogn)。在GA中利用Greedy(X)对不满足约束条件的个体进行处理,使得满足约束条件的个体在处理后能够放入背包中,不再需要重新产生新的个体,这样既提高了算法的全局寻优能力,又加快了算法的收敛速度。
下面将GA与Greedy(X)结合给出算法GA1。令Xbes(t)表示种群P(t)中最优个体,Xworst(t)表示种群P(t)中最差个体,f(Xbes(t))和f(Xworst(t))分别为它们的适应度,算法的最大迭代次数为T,则GA1的算法描述如下。
算法3 GA1算法
(1)输入0-1KP问题实例;
(2)随机生成初始种群P(0)={Xi(0)∈{0,1}n|1≤i≤M};
(3)计算f(Xi(0))(1≤i≤M),当f(Xi(0))>C时调用Greedy(Xi(0));
(4)确定Xbes(0)和Xworst(0),并令t=0;
(5)如果t>T,则转至(10)执行;
(6)对种群P(t)进行交叉、变异、选择操作,产生新种群P(t+1);
(7)计算f(Xi(t+1))(1≤i≤M),当f(Xi(t+1))>C时调用 Greedy(Xi(t+1));
(8)确定Xbes(t+1)和Xworst(t+1),若f(Xworst(t))>f(Xbes(t+1))则Xworst(t+1)=Xbes(t);
(9)置t=t+1,并转(5)执行;
(10)输出Xbes(t)和f(Xbes(t)),算法结束。
由于Greedy(X)的时间复杂度是多项式时间的,在GA1中调用Greedy(X)的次数不超过算法迭代次数的M倍,而算法3迭代次数是关于n的多项式,因此GA1仍是具有多项式时间复杂度的随机算法。
3.2 利用GA求解3-SAT问题
在利用GA求解3-SAT问题时,为了克服GA易于陷入局部最优的缺点,在GA中引入局部搜索算法(local search algorithm,LSA)[9,11,13]以避免其陷入局部最优的缺点。
下面首先给出LSA的算法描述。记个体X=(x1,x2,…,xm)∈{0,1}m,这里m 为合取范式A中的变元个数。又令g(X)表示以X=(x1,x2,…,xm)为指派时A中可满足子句的个数。g(~X)表示以X=(x1,x2,…,xm)为指派,且取反某个基因座之后A中可满足子句的个数。K[1…m/3]用于存储不满足子句个数的减少值,Kmax表示该数组中的最大值。则LSA的算法伪代码描述如下。
算法4 LSA(X)
(1)for j=m/3 to(m/3)*2do
(2) xj=1-xj;
(3) K[j]=g(~X)-g(X);
(4) xj=1-xj;
(5)end for;
(6)确定K[m/3…(m/3)*2]中的最大值Kmax及其对应的基因座k;
(7)将X中基因座k的值取反;
(8)输出X,算法结束。
在LSA中,算法通过尝试改变某基因座的值以使个体不满足3-SAT的子句的个数减少,找到使得子句个数减少最多的基因座,并将其值取反所得新个体必是局部最优的。LSA使得个体在改变最少的情况下得到最佳的优化结果,其时间复杂度是O(m)。
以下将LSA与GA相结合给出求解3-SAT问题的混合遗传算法GA2。令Xbes(t)表示种群P(t)中最优个体,Xworst(t)表示种群P(t)中最差个体,f(Xbes(t))和f(Xworst(t))分别为它们的适应度,算法的最大迭代次数为T,则GA2的算法描述如下。
算法5 GA2算法
(1)输入3-SAT问题实例;
(2)随机生成初始种群P(0)={Xi(0)∈{0,1}n|1≤i≤M};
(3)调用LSA(Xi(0))(1≤i≤M),并令t=0;
(4)计算f(Xi(t))(1≤i≤M),并确定Xbes(t)和Xworst(t);
(5)如果t>T,则转至(11)执行;
(6)对种群P(t)进行交叉、变异、选择操作,产生新种群P(t+1);
(7)调用LSA(Xi(t+1))(1≤i≤M);
(8)计算f(Xi(t+1))(1≤i≤M),并确定Xbes(t+1)和Xworst(t+1);
(9)若f(Xbes(t+1))<f(Xworst(t))则 Xworst(t+1)=Xbes(t);
(10)置t=t+1,并转(5)执行;
(11)输出Xbes(t)和f(Xbes(t)),算法结束。
由于LSA的时间复杂度是O(m),因此易知算法GA2是求解3-SAT问题的具有多项式时间复杂度的随机算法。
4 仿真实验与分析
为了验证GA1和GA2求解0-1KP问题与3-SAT问题的可行性和有效性,下面分别利用GA1与GA2求解0-1KP实例和3-SAT实例,并将计算结果与相关算法分析比较,从而验证GA1与GA2的性能。计算所使用的微型机的配置如下:CPU为Intel(R)Core(TM)i3,主频2.53GHz,内存为4G,操作系统为Microsoft Windows 7。所有算法均利用VC 6.0编程实现。
4.1 基于GA1求解0-1KP实例的结果与分析
下面首先给出两个较大规模的0-1KP的实例[14]。
0-1KP实例1.给定50个物品,物品价值集为{3,13,10,13,5,6,6,3,11,3,9,2,7,9,7,4,6,3,9,4,9,5,8,9,10,14,7,8,7,9,5,5,11,7,5,11,6,9,8,9,11,8,5,10,10,9,10,8,10,12},物品重量集为{2,5,1,9,3,6,4,9,3,2,8,9,6,2,5,2,5,9,4,2,3,4,8,5,4,3,1,2,1,1,3,3,6,3,1,2,1,4,1,1,4,5,3,5,5,2,6,1,5,3},背包容量为80。
0-1KP实例2.给定200个物品,物品价值集为{98,42,27,4,41,85,38,52,26,12,44,87,92,45,95,23,44,48,75,20,57,25,66,62,90,31,9,97,81,83,54,74,92,54,88,81,70,96,44,84,36,74,50,38,27,58,82,50,40,2,25,71,65,21,14,50,59,34,60,38,42,17,69,80,76,38,91,58,85,38,75,91,27,39,80,90,72,32,59,80,49,66,54,20,88,33,68,21,98,58,86,38,43,61,13,88,27,41,44,68,18,59,32,17,5,86,23,47,95,46,22,35,54,11,9,40,61,41,11,8,34,2,4,100,28,54,16,58,44,45,67,23,10,44,84,22,61,13,54,14,52,81,91,40,63,73,76,67,89,19,61,40,3,15,51,69,89,36,42,46,9,55,57,69,98,63,41,46,2,5,89,16,64,49,77,53,76,70,95,87,82,26,19,33,92,83,78,83,92,3,63,59,89,82,45,5,46,1,33,54},物品重量集为{8,20,18,8,8,10,20,13,15,18,8,12,18,3,18,3,18,7,12,11,15,2,4,6,4,18,9,7,18,19,15,1,3,11,20,17,20,4,6,7,3,13,17,17,4,2,1,1,4,7,20,10,1,19,20,5,11,12,1,7,3,10,6,20,11,13,2,20,1,4,18,18,20,6,12,12,1,12,19,15,16,58,6,2,2,1,6,6,15,8,11,12,14,3,16,6,15,19,20,9,4,16,3,14,5,3,17,19,15,10,2,9,7,13,13,3,9,1,6,20,8,15,8,17,19,6,20,17,1,20,11,12,4,10,15,2,7,17,10,6,12,4,4,12,2,20,6,5,13,12,5,5,19,4,19,17,2,17,12,16,18,2,18,14,12,1,10,6,10,2,18,20,18,7,1,14,7,5,17,5,13,9,3,11,19,10,7,9,1,15,17,11,15,19,7,4,4},背包容量为1000。
算法GA1和GA的参数设置为:迭代次数置为200,群体规模为40,交叉概率为0.8,变异概率0.085。在表1中统计出三种算法求解实例1和实例2的最好结果(Best)和平均结果(Mean),其中Mean取自10次实验数据的平均结果。这些数据与基本GA以及改进的BFO算法[14]的数据进行比较,计算结果如表1所示。

表1 GA1、改进BFO和GA求解0-1KP实例的结果比较
通过比较发现:对于0-1KP实例1,GA1求得的最好值比GA和改进BFO更优,其平均值与改进BFO相差不大,但明显优于GA。对于0-1KP实例2,GA1求得的最好值和平均值明显比GA和改进BFO要优很多。以上对比表明,对于0-1KP问题GA1的求解效果相比GA和改进BFO均优,特别是当实例规模增大时,GA1求解效果的优越性更加明显,因此GA1是一种求解0-1KP问题可行且有效的算法。
4.2 基于GA2求解3-SAT实例的结果与分析
为了验证GA2求解3-SAT问题的可行性与有效性,下面分别利用GA2和GA求解一系列随机生成的3-SAT实例,实例的规模由(m,n)表示,其中m为变元个数,n为子句个数。计算结果见表2中。
在GA2和GA中,参数设置为:种群规模为10,最大迭代次数为200,交叉概率为0.6,变异概率为0.1。在表2中,分别给出了两种算法得到可满足解的比率(Suc)和实验次数(Test),以及GA2相比GA得到可满足解的成功率的增值(Imp)。

表2 GA2和GA求解3-SAT实例的结果比较
由表2可以看出:在实验次数、变元数和子句数相同情况下,GA2比GA的求解性能更高,GA2得到可满足解的成功率比GA平均提高了近3.2%,可见基于LSA对GA的改进是非常成功的,即GA2是一种适于求解3-SAT问题的有效算法。
5 结束语
首先分别介绍了0-1KP和3-SAT的数学模型,给出了基本遗传算法的实现流程;然后分别基于GA与贪心策略相结合、局部搜索相结合求解0-1KP问题和3-SAT问题,给出了相应的改进算法GA1和GA2。仿真计算结果表明:本文所提出的改进遗传算法是求解0-1KP和3-SAT问题行之有效的方法。
[1] 郑宇军,薛锦云,凌海风.组合优化问题简约与算法推演[J].软件学报,2011,22(9):1985-1993.
[2] 贺毅朝,刘坤起,张翠军,等.求解背包问题的贪心算法及其应用[J].计算机工程与设计,2007,28(11):55-57.
[3] 曹国生,贺毅朝,李敏,等.基于改进的遗传算法求解可满足性问题[J].现代计算机,2008,28(4):16-19.
[4] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[5] M.H.Alsuwaiyel(著),吴伟昶,方世昌(译).算法设计技巧与分析[M].北京:电子工业出版社,2004.8.
[6] 贺毅朝,王彦祺,寇应展.一种求解3-SAT问题的新方法[J].计算机工程与应用,2006,42(16):70-72.
[7] 曾国清.0-1背包问题的遗传算法求解[J].高校理科研究,2006,3:242-243.
[8] 田奕,刘涛,李国杰.求解可满足问题的一种高效遗传算法[J].模式识别与人工智能,1996,9(3):209-212.
[9] Zbigniew Michalewicz(著),曹宏庆(译).如何求解问题——现代启发式方法[M].北京:中国水利水电出版社.
[10] 王秋芬,梁道雷.一种求解0-1背包问题的算法[J].计算机技术与发展,2013,23(1):123-127.
[11] 岳琪,宋文龙.遗传算法与组合优化问题研究[J].信息技术,2004,28(1):53-54.
[12] 耿素云,屈婉玲,王捍贫.离散数学教程[M].北京:北京大学出版社,2002.
[13] 张宏斌.组合优化问题的启发式搜索[J].计算机科学,1998,25(2):13-16.
[14] 杜明煜,雷秀娟.改进的细菌觅食优化算法求解0-1背包问题[J].计算机技术与发展,2014,24(5):44-47.
