四种卡尔曼滤波器在仅视线测量相对导航中的性能比较*

刘承奇，贾英宏，徐世杰

(北京航空航天大学宇航学院，北京100191)

0 引言

视线测量相对导航的基本原理是通过测量目标的视线信息来确定目标相对于观测者的位置，它是一种简单、有效、低成本的导航方法，在很多领域中都得到了应用［1］.然而，将仅有视线测量的相对导航应用在航天器交会操作中则存在一个严重缺点:缺少相对距离的直接测量信息，导致系统的导航精度低.为了解决这个难题，一些学者提出的可行性办法主要有两种:一是通过追踪航天器进行特定轨道机动来引入距离信息［2-4］;二是获取目标航天器上多个特定位置标识点的视线信息［4-6］来提高导航精度.追踪航天器进行轨道机动需要消耗一定数量的推进剂，而获取目标器上多个特定位置标识点的视线信息需要目标器是合作的且需要追踪器在近距离条件下观测.与之不同，本文的主要目的是仅从滤波器角度出发，研究并比较EKF、UKF及它们的平方根形式(SREKF和SRUKF)估计相对距离的精度.

EKF滤波的基本原理是将非线性的状态方程或量测方程线性化处理后进行标准卡尔曼滤波，但线性化过程中高阶(三阶以上)项的舍弃及滤波计算中舍入误差的积累会导致滤波精度下降，甚至使状态协方差阵失去非负定性，进而导致滤波发散.UKF滤波通过对非线性函数的概率密度分布进行近似，使近似的精度提高到三阶，而其计算量与EKF同阶.平方根形式的滤波可严格保证滤波过程中误差协方差阵的正定性.本文给出了3种典型相对运动模型仅视线测量相对导航中EKF、SREKF、UKF和SRUKF 4种滤波器的性能比较，将平均距离误差作为距离提取能力的判断指标.

1 滤波算法介绍

考虑系统噪声和观测噪声，非线性系统表示为

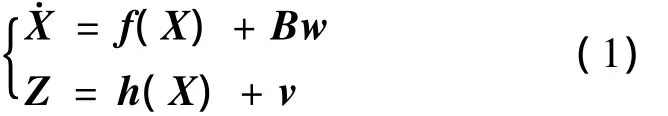
式中，X为n维系统状态变量，Z为观测量，f和h分别表示系统状态函数和观测函数，B为噪声驱动阵，w为系统噪声，v为观测噪声.假设w和v都为零均值白噪声，w～N(0，Q)，Q为系统噪声阵，v～N(0，R)，R为量测噪声阵.图1～4给出了EKF、SREKF、UKF和SRUKF 4种滤波算法流程图.

图1中Δt表示离散化步长，P为状态误差协方差矩阵，Φ为状态转移矩阵，H为观测对状态的Jacobi矩阵，K 为滤波增益.Φk，k-1、Hk和 Qk-1计算方法如下

图2算法中，S为P的平方根，chol为矩阵cholesky 分解函数，MGS 为Modified Gram-Schmidt算法［7］.

图3算法中n表示状态变量的个数，其中系数γ、和与滤波参数α、β 和κ 的关系如下:

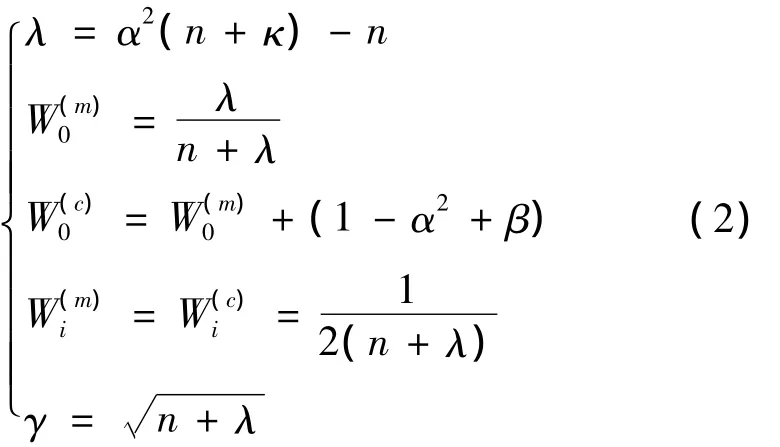
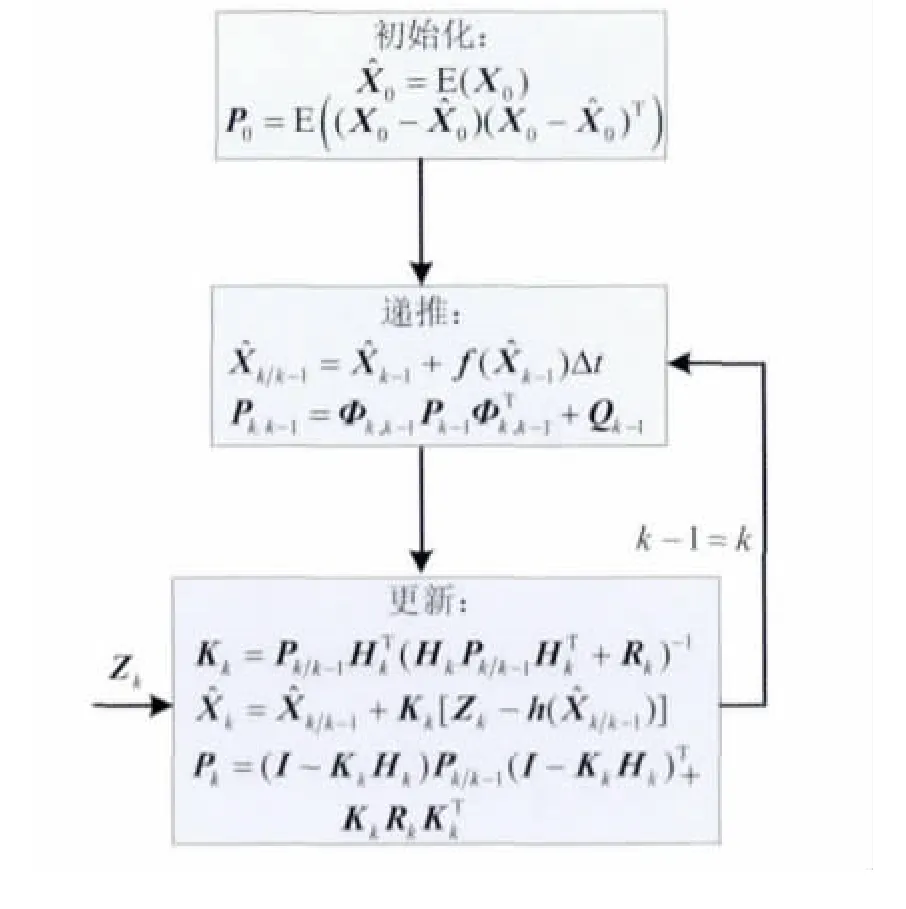
图1 EKF算法流程Fig.1 Extended Kalman filter algorithm

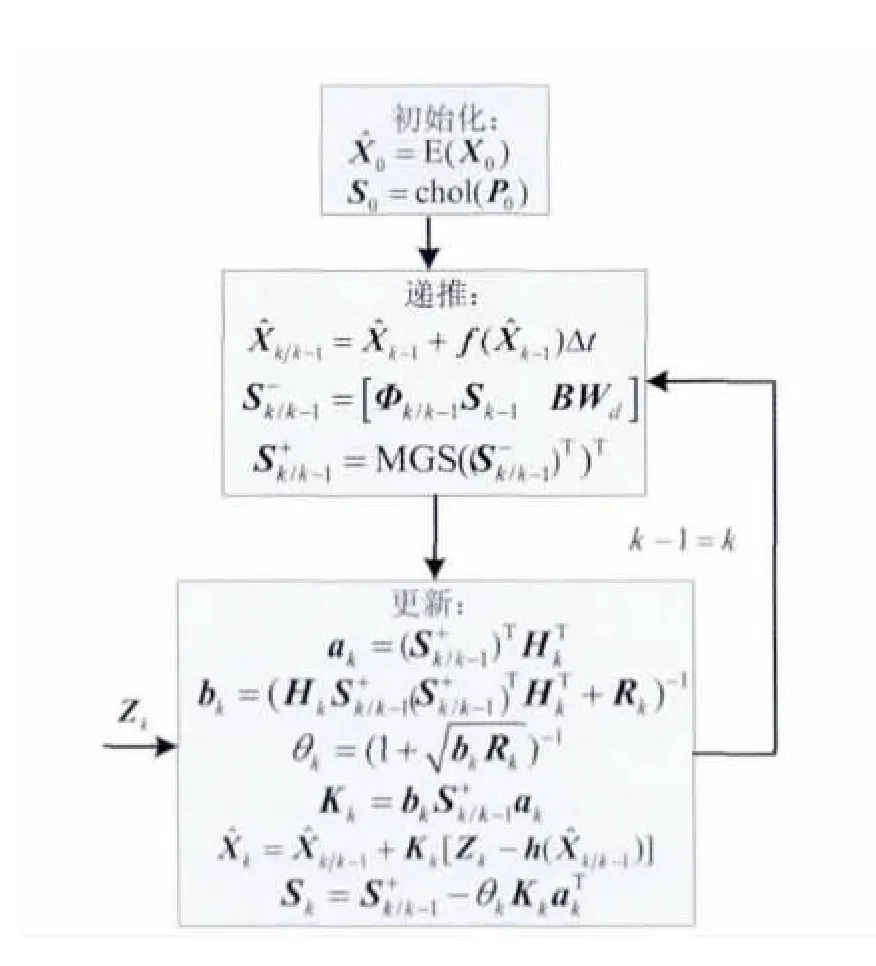
图2 SREKF算法Fig.2 Square-root extended Kalman filter algorithm

图4中qr为矩阵QR分解函数，cholupdate为矩阵Cholesky分解的秩1修正函数.chol、qr和cholupdate三函数为Matlab函数.

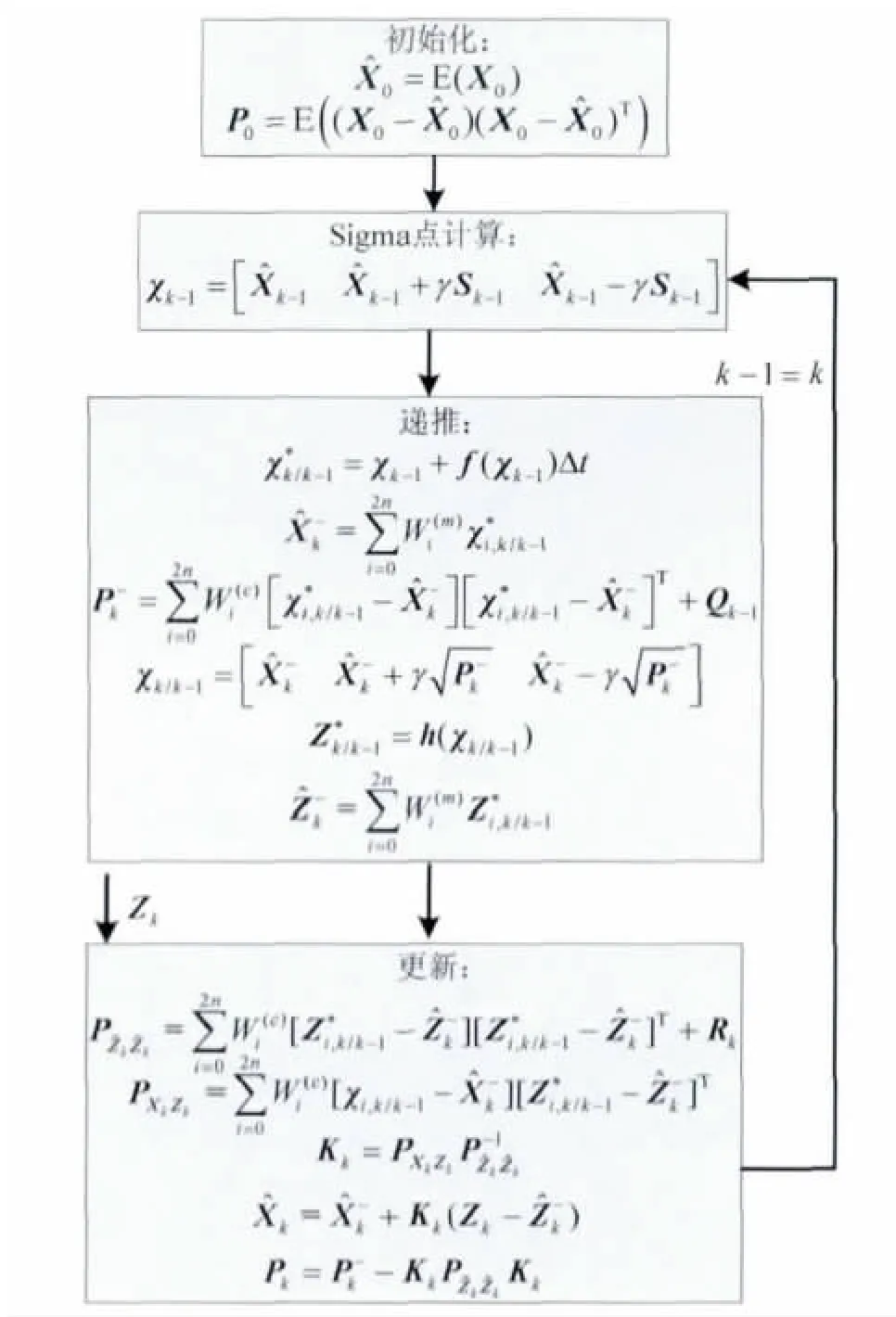
图3 UKF算法流程Fig.3 Unscented Kalman filter algorithm

2 仅视线测量相对导航的数学模型

2.1 相对动力学方程

目标航天器和追踪航天器惯性系下的运动方程分别如下:

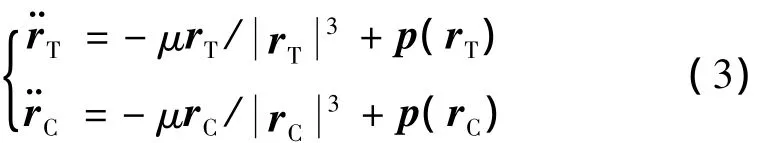
式中，rT和rC分别表示目标航天器和追踪航天器的位置矢量，如图5所示.μ为地球引力常数，p(*)表示摄动加速度项，包括地球引力J2、J3和J4摄动项等.图5中的OXOYOZO坐标系为建立在追踪航天器轨道上的转动坐标系，其坐标原点O位于追踪航天器质心，OZO指向地心，OYO指向航天器角动量方向，OXO与OYO和OZO构成右手坐标系.

目标航天器相对于追踪航天器的相对位置转动矢量定义为Δr=rT-rC.假设两航天器相对距离远小于它们的地心距离，对相对运动方程进行线性化处理可得:

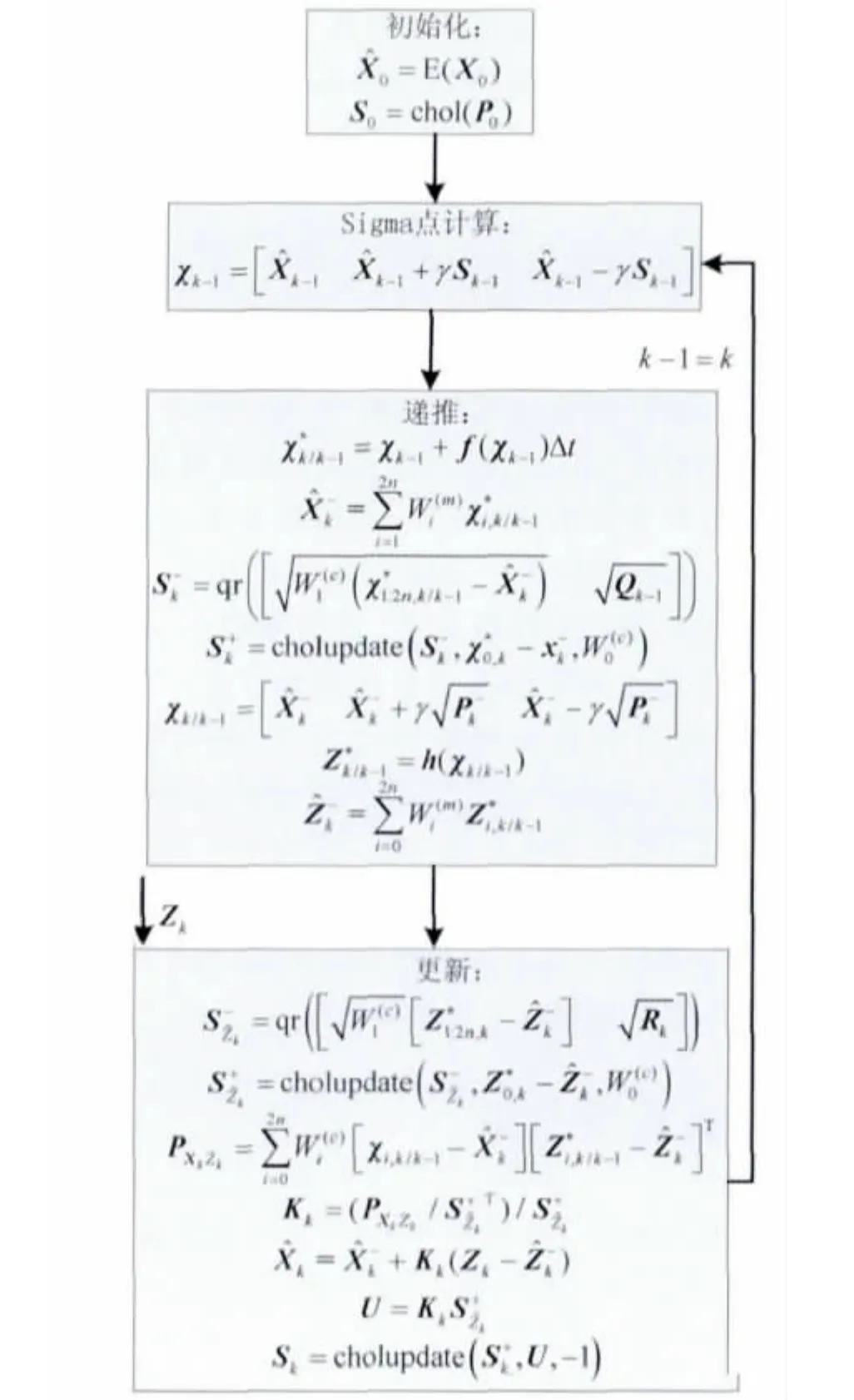
图4 SRUKF算法流程Fig.4 Square-root unscented Kalman filter algorithm

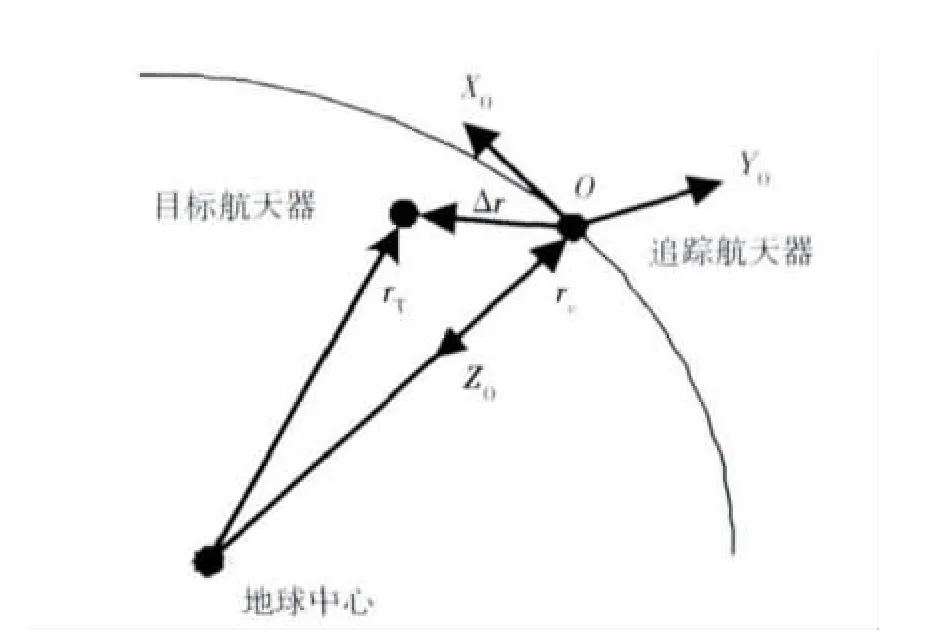
图5 追踪航天器轨道坐标系Fig.5 The orbit frame of the chaser spacecraft

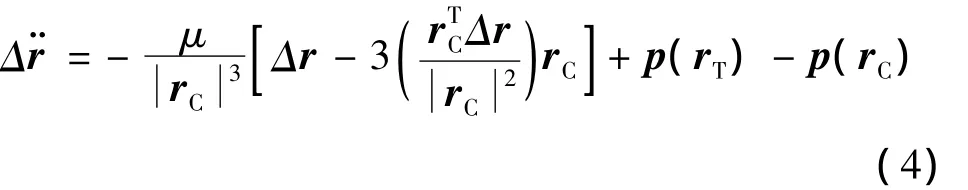
2.2 状态方程

取该相对导航系统的状态变量为

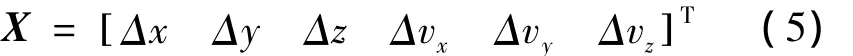
由式(4)和式(5)得出相对导航系统的状态方程:

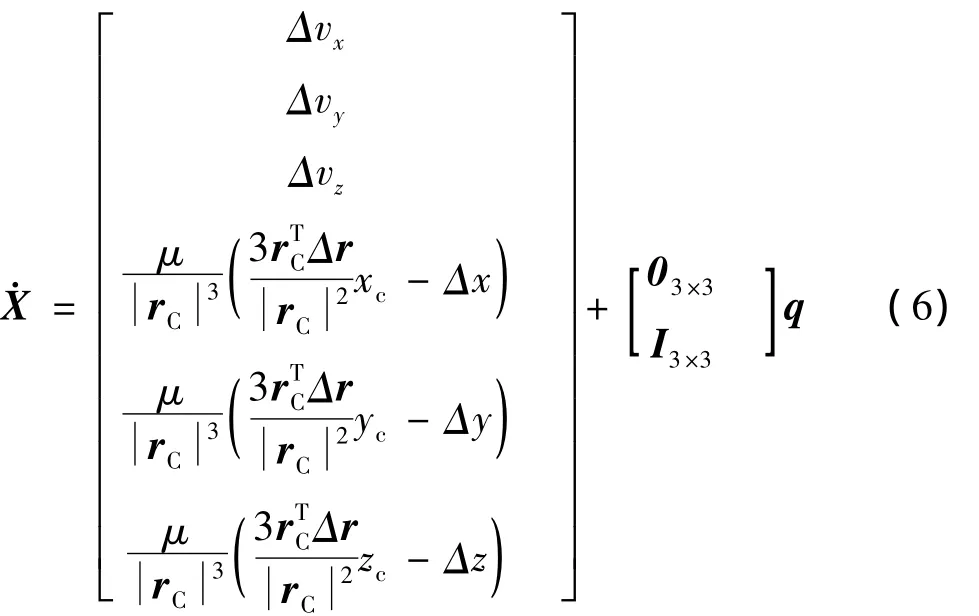
式中，xc、yc和zc为rC在惯性系下沿各坐标轴的分量，q为两航天器的地球引力J2、J3和J4项摄动项等之差，如式(4)中的p(rT)-p(rC)，假设它是零均值高斯白噪声，它的方差特性如下:

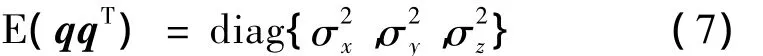
线性化处理后的系统状态转移矩阵可以近似表示为

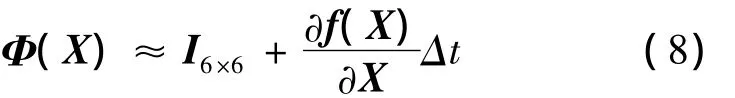
2.3 观测方程

视线测量定义在追踪航天器轨道坐标系，其中方位角ε和俯仰角φ定义如图6所示，则系统的观测方程为

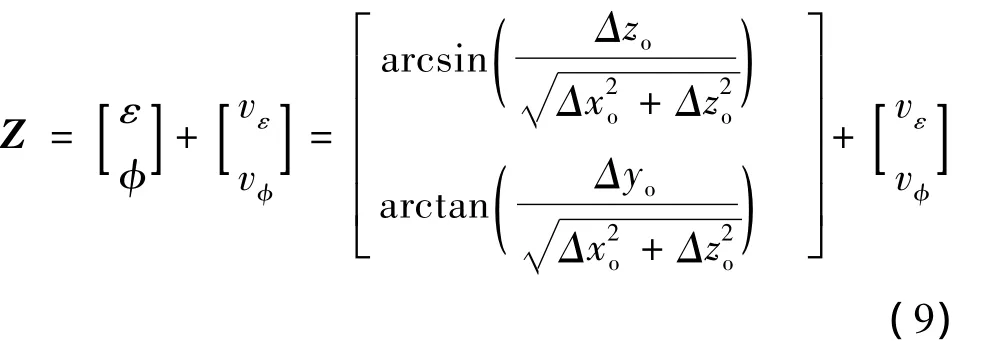
式中，vε和vφ分别为方位角ε和俯仰角φ的观测噪声，其中观测的Jacobi矩阵H计算方法如下:

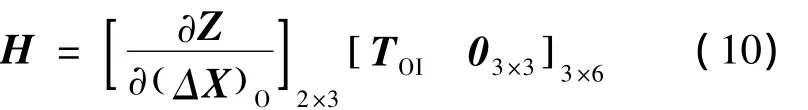
其中TOI为惯性系到追踪星轨道系的转换矩阵.

平均相对距离误差ρ，如图6所示，定义为

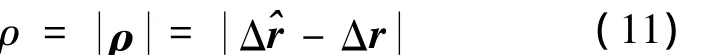
3 数值实例

本文针对航天器间的3种典型的相对轨道进行仿真.第1种为相对保持型，追踪航天器位于目标航天器后方1 km处;第2种为椭圆型，目标航天器在追踪航天器轨道平面内的运动轨迹为2 km×1 km的椭圆;第3种漂移型，目标航天器位于追踪航天器下方500 m.3种相对运动示意图如图7所示.其中目标航天器和3种相对运动对应的追踪航天器的初始轨道要素:半长轴a、偏心率e、轨道倾角i、升交点赤径Ω、近地点幅角ω和平近点角M如表1所示.

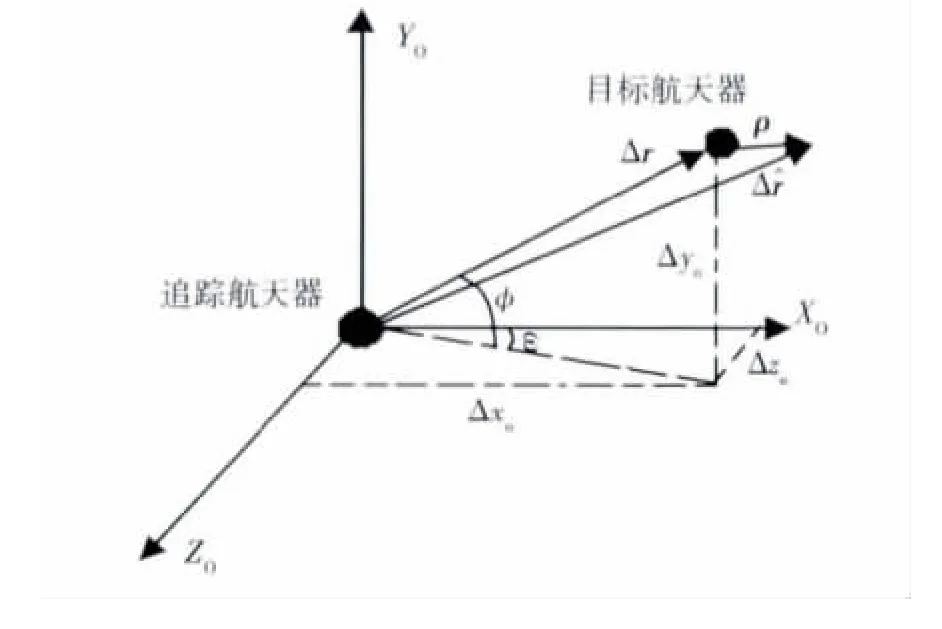
图6目标航天器相对于追踪航天器的视线测量Fig.6 Line-of-sight measurement from the chaser spacecraft to the target spacecraft

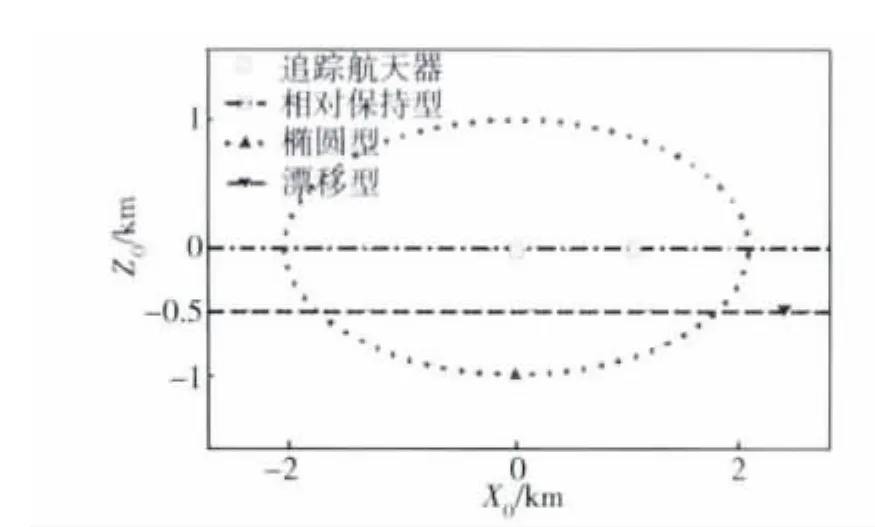
图7 3种相对运动的示意图Fig.7 Geometry of the three relative motions

采用4阶龙格-库塔方法对航天器轨道进行仿真，并考虑地球引力J2、J3和J4项摄动影响，仿真步长为0.4 s.光学敏感器的测角精度为0.01°，系统噪声的标准差σx=σy=σz=1×10-6m/s2.^X0=X0+［50 m，50 m，50 m，0.1 m/s，0.1 m/s，0.1 m/s］，P0=diag{502，502，502，0.12，0.12，0.12}，UKF 及 SRUKF中的滤波参数为α=1×10-3，β=2，κ=0.基于上述仿真条件，在相同的初始条件下采用4种滤波器对3种相对运动模型进行仿真，仿真结果如图8～10所示，图中的小坐标系为原坐标系某时间区间段(矩形框)内的局部放大图.

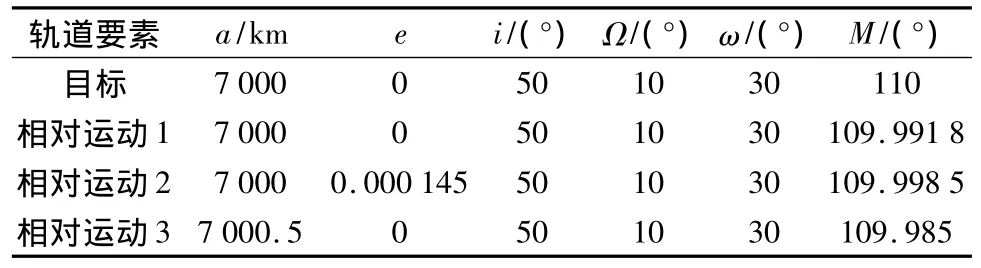
表1 初始轨道要素Tab.1 Initial orbit elements

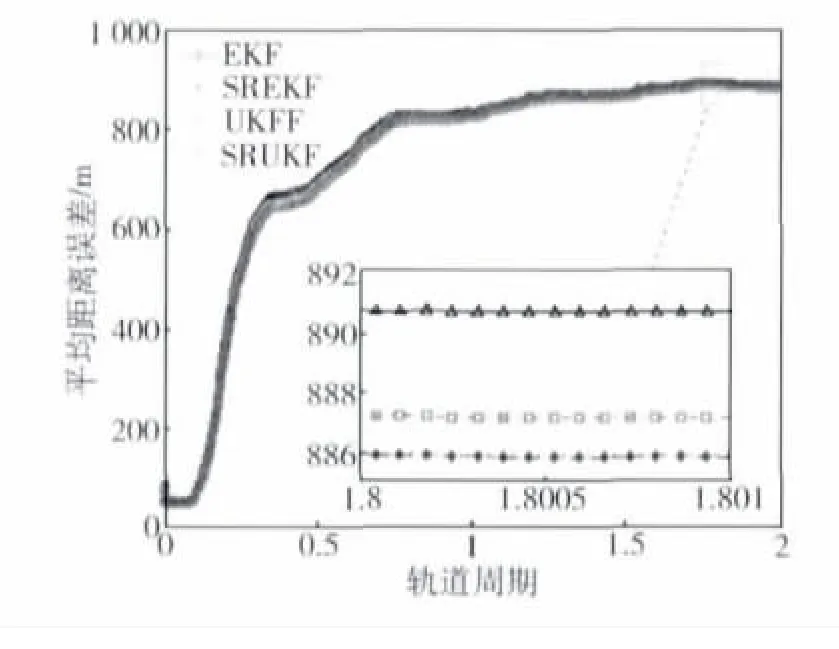
图8 相对保持运动平均距离误差Fig.8 Average distance error for the hold relative motion

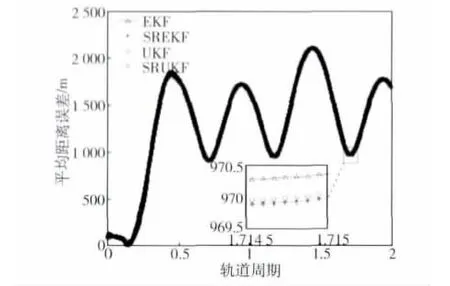
图9 椭圆相对运动平均距离误差Fig.9 Average distance error for the ellipse relative motion

由图8～10可知，3种相对运动的平均距离误差都逐渐增大且有发散趋势，这是由仅视线测量相对导航无法测量相对距离信息引起的.对比图中4种滤波器的平均距离误差可知:UKF的估计精度稍高于EKF的精度，这是由于UKF为三阶近似，而EKF的为两阶近似;SREKF的估计精度稍高于EKF，SRUKF的估计精度稍高于UKF的精度，这是因为状态误差协方差阵正定性的逐渐丧失会引起Kk的失真从而造成从残差中提取的补偿信息错误量增多，导致滤波误差越来越大，而平方根形式的滤波器在滤波过程中可保证状态协方差阵是对称的正定阵，从而可保证估计精度，在仿真中SREKF的估计精度稍高于UKF的估计精度也能体现该结论.图8和图9小坐标系中SREKF和SRUKF的滤波曲线基本重合，说明其估计精度基本一致，图10中SRUKF的估计精度稍优于SREKF.

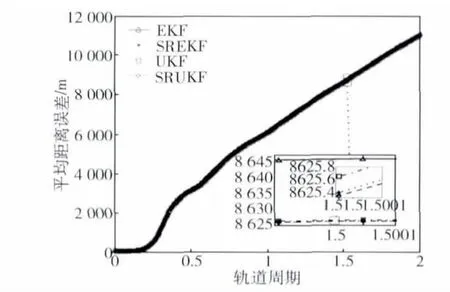
图10 漂移型相对运动平均距离误差Fig.10 Average distance error for the drifting relative motion

由图8～10可知，虽然4种不同的滤波算法相对距离的估计精度有一定的差别，但差别不明显.4种算法的相对距离误差在同一量级且都有发散趋势，故4类不同的卡尔曼滤波器对提高仅视线测量相对导航中相对距离估计精度的贡献不大.

4 结论

本文针对航天器间的仅视线测量相对导航问题，比较了 EKF、SREKF、UKF和 SRUKF滤波器提取相对距离信息的能力.经过建模仿真得到如下结论:在航天器间仅视线测量相对导航中，EKF、SREKF、UKF和SRUKF这4种滤波算法的估计精度位于同一量级;UKF的估计精度稍优于EKF;平方根形式的滤波器(SREKF、SRUKF)的估计精度稍优于标准滤波器(EKF、UKF).

［1］SCHMIDT J，GELLER D.Viability of angles-only navigation for orbital rendezvous operation［R］.AIAA 2010-7755，2010.

［2］CHARI R J V.Autonomous orbital rendezvous using angles-only navigation［D］.Gambridge:Massachusetts Institute of Technology，2001.

［3］LI J R，LI H Y，TANG G J，et al.Research on the strategy of angles-only relative navigation for autonomous rendezvous［J］.Science China:Technology Science，2011，54(7):1865-1872.

［4］WOFFINDEN D C.Angles-only navigation for autonomous orbital rendezvous［D］.Logan，Utah:Utah State University，2008.

［5］WOFFINDEN D C，GELLER D K.Relative angles-only navigation and pose estimation for autonomous orbital rendezvous［J］.Journal of Guidance，Control，and Dynamics，2007，30(5):1455-1469.

［6］SUN D，CRASSIDIS J L.Observability analysis of sixdegree-of freedom configuration determination using vector observations［J］.Journal of Guidance，Control and Dynamics，2002，25(6):1149-1157.

［7］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998:92-102.