基于路的多重完全图相关图生成树计数

谭秋月

（武夷学院数学与计算机系，福建武夷山354300）

基于路的多重完全图相关图生成树计数

谭秋月

（武夷学院数学与计算机系，福建武夷山354300）

利用图G的标定技巧、矩阵和行列式运算、补生成树矩阵定理、不等式运算等理论，研究了当m=2, 3, 4, 5，且a1, a2, …, am为任意数时，基于路的多重完全图相关图一般情况的生成树数目，并得到了相关公式。

多重完全图相关图；生成树；补生成树矩阵定理

0 引言

图的生成树数目是图的重要不变量之一，其应用广泛。例如在网络可靠性方面有重要应用：一个网络可以用一个图G来模拟，这个网络中所有的站点之间可以互相通讯，意味着图G中必须包含一个生成树，因此，图的生成树的数目是评价该图（网络）可靠性的重要指标之一，最大化生成树的数目是加强网络可靠性的一个途径。

如果能得到一个图G生成树数目的计数公式对确定图G在完全图Kn中的补图（即补图类Kn-G，其中）的生成树数目的计数公式也很有意义。文献[1-3]给出了基于路的多重完全图相关图补图类。本文讨论当m=2, 3, 4, 5时基于路的多重完全图相关图生成树的数目，并求出一般情况下（即a1, a2, …, am为任意数时）的计数公式。

1 图的定义

假设G1=(V1, E1)和G2=(V2, E2)没有公共顶点，以V1∩V2为顶点集，以E1, E2和为边集所组成的图，称为G2和G2的联图，记为[4]。

特别地，一个顶点和完全图Km的联图Km+1为完全图，如图1所示。

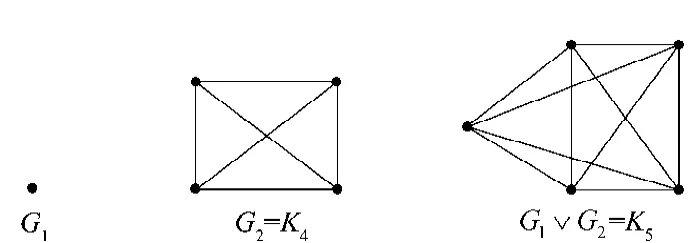
图1 Fig.1

定义1[3]由m个完全图Ka1+1, Ka2+1, Kam+1和连接这m个完全图上的任意一点形成的路Pm所组成的图，称为一个基于路的多重完全图，记为。

定义2[3]如果基于路的多重完全图满足ai≥2(i=1, 2, …, m)以及n≥m+ a1+…+am，在完全图Kn中删去图所有的边后组成的图称为基于路的多重完全图相关图，记为。

图2为一个基于路的4重完全图PK4(2, 2, 3, 2)，图3为一个基于路的4重完全图相关图K15-PK4(2, 2, 3, 2)的补图。

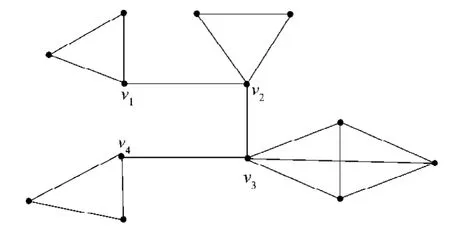
图2 (2, 2, 3, 2)Fig.2(2, 2, 3, 2)

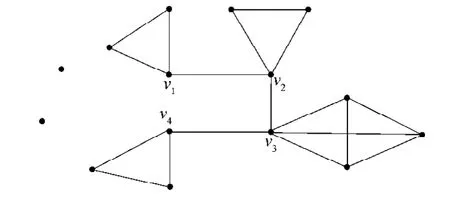
图3 Fig.3

本文仅讨论m=2, 3, 4, 5，且a1, a2, …, am为任意数时，多重完全图相关图生成树数目的计数公式。

2.1 结论

定理1当m=2，且a1, a2为任意数时，基于路P2的多重完全图相关图的生成树数目为

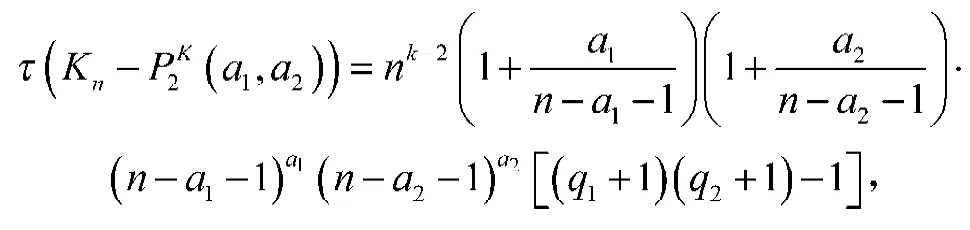
特殊地，当m=2，a1=a2=a时，的生成树数目为

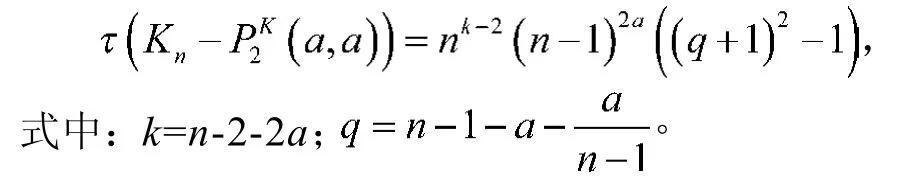
定理2当m=3，且a1, a2, a3为任意数时，基于路P3的多重完全图相关图的生成树数目为

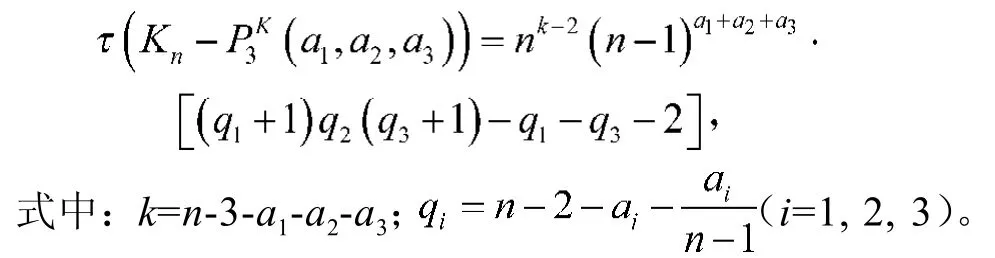
特殊地，当m=3，a1=a2=a3=a时，的生成树数目为

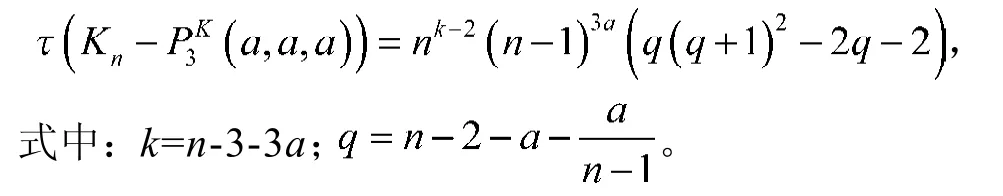
定理3当m=4，且a1, a2, a3, a4为任意数时，基于路P4的多重完全图相关图的生成树数目为

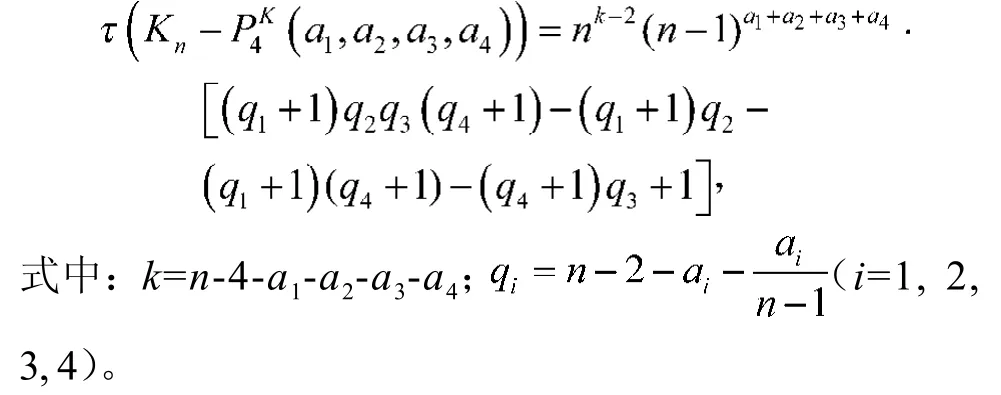
特殊地，当m=4，a1=a2=a3=a4=a时，的生成树数目为

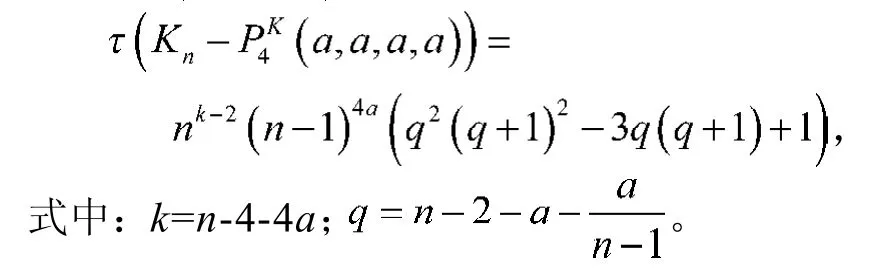
定理4当m=5，且a1, a2, a3, a4, a5为任意数时，基于路P5的多重完全相关图的生成树数目为

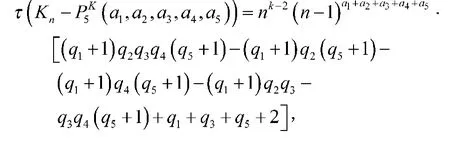
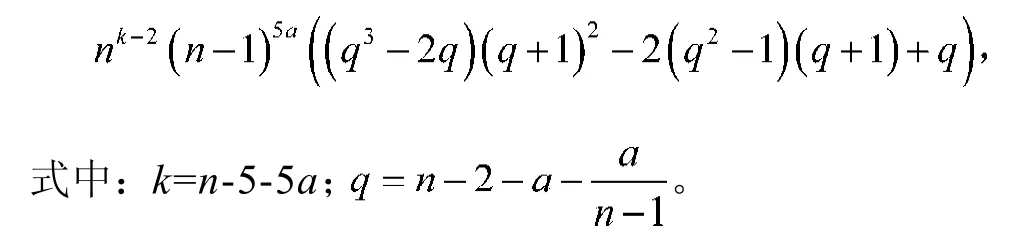
2.2 结论的证明

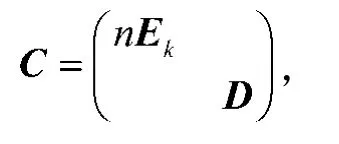
式中

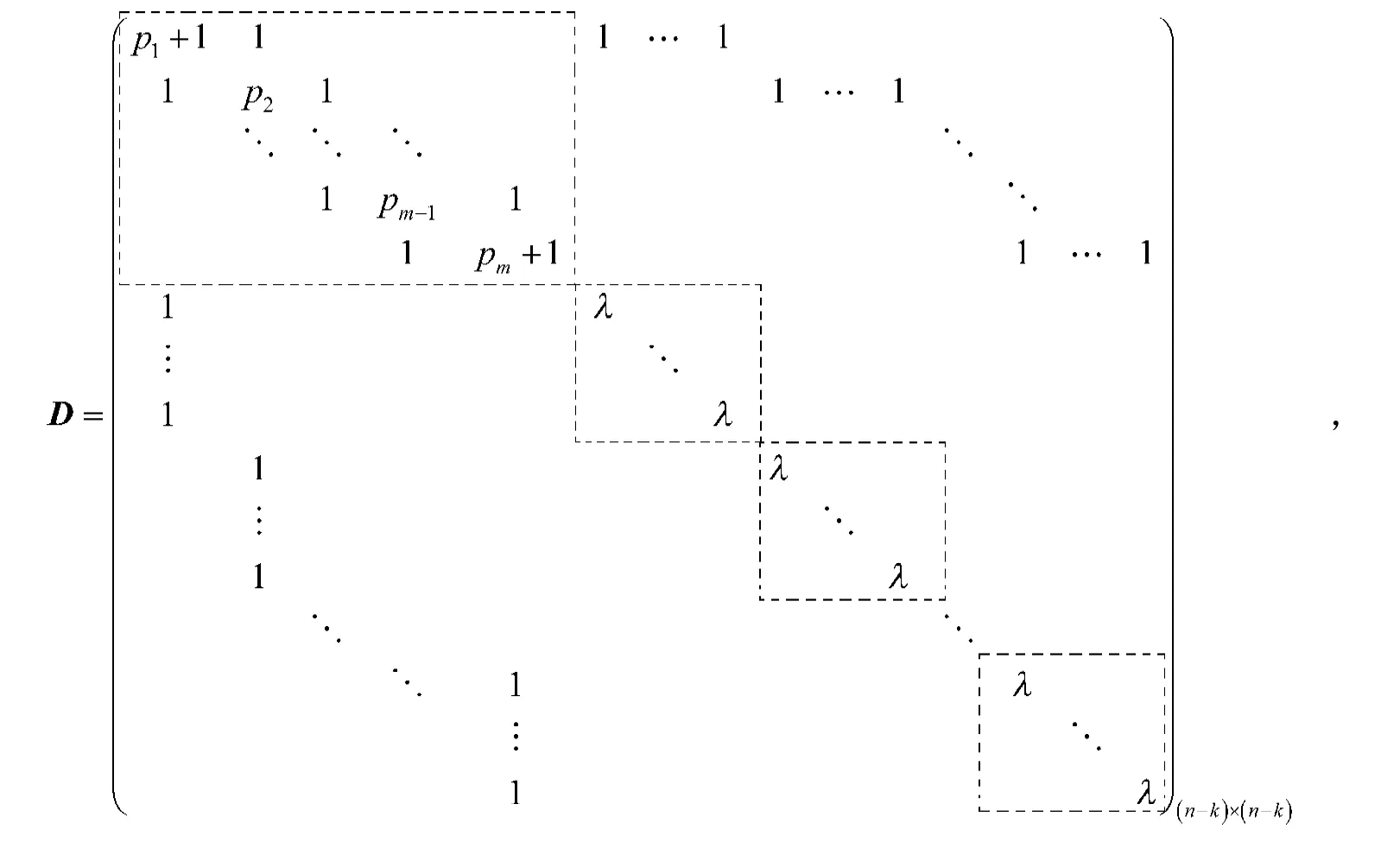
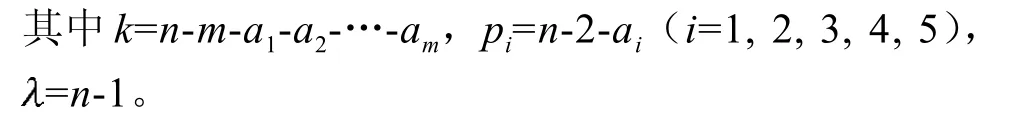
因此，根据补生成树矩阵定理[1]，生成树的数目为。

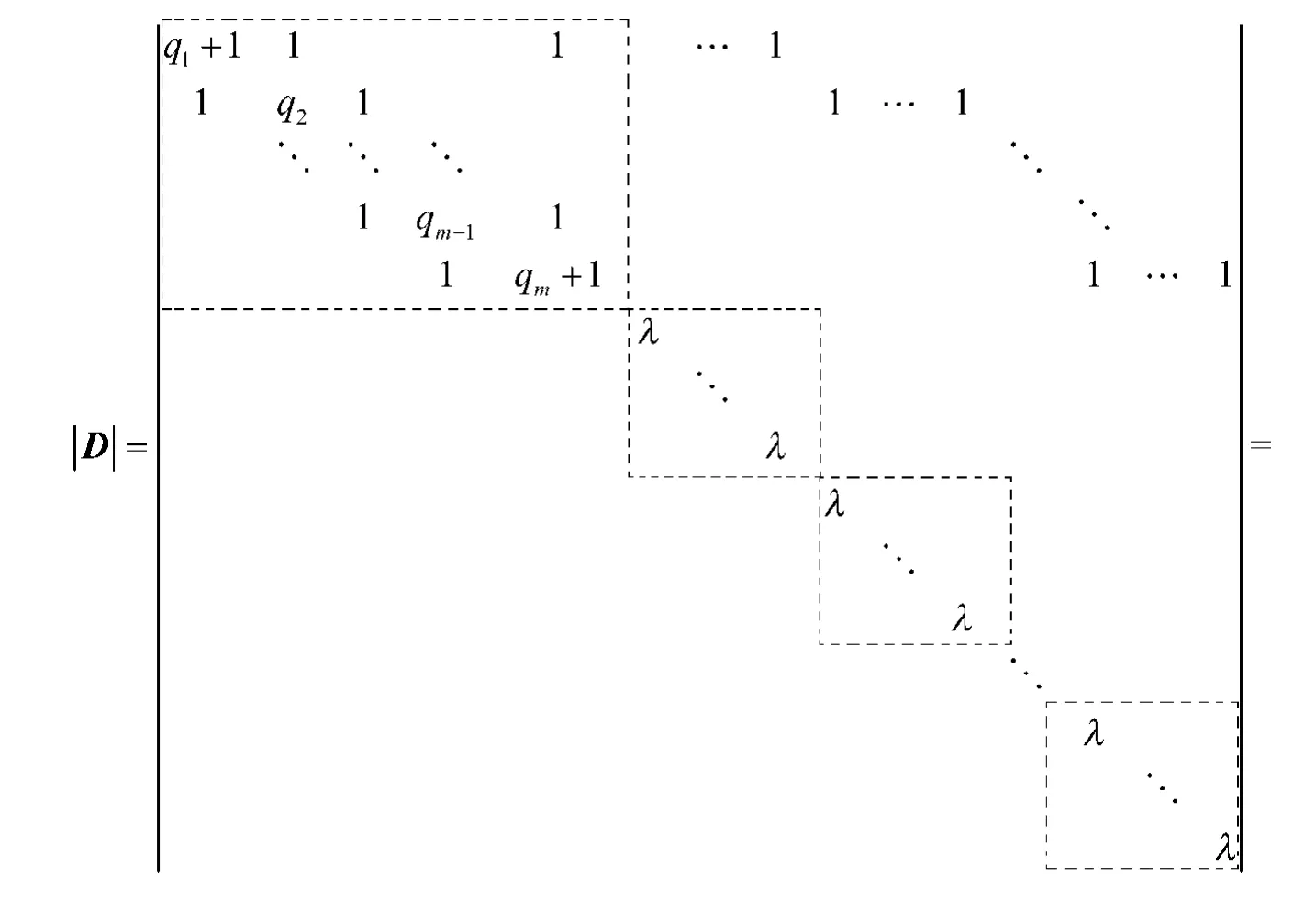
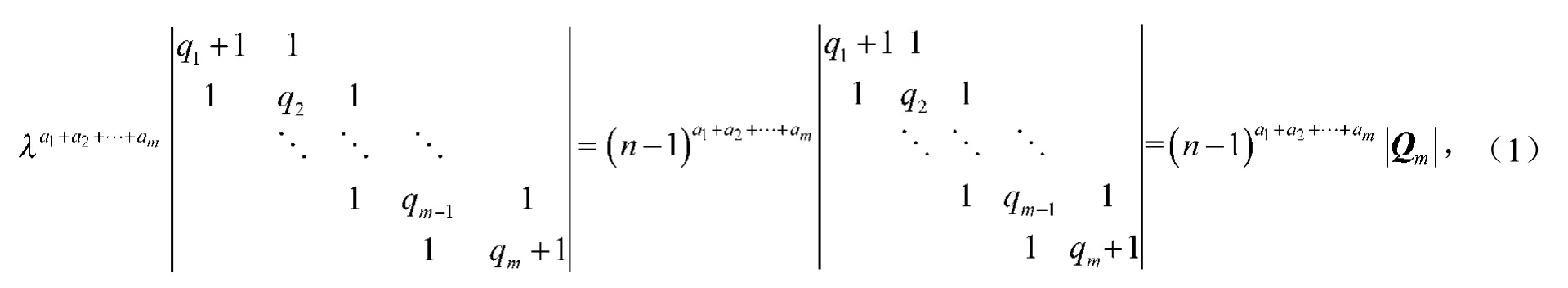
3 结语

对定理1至定理4中的生成树数目公式进行比较，没有找到规律，目前无法用数学归纳法推导出图更一般（即m为任意大于1的整数时）的生成树数目的公式，希望在进一步工作中有所突破。

[1]Nikolopoulos S D，Rondogiannis P. On the Number of Spanning Trees of Multi-Star Related Graphs[J]. Information Processing Letters，1998，65(4)：183-188.

[2]Yan W M，Myrvold W，Chung K L. A Formula for the Number of Spanning Trees of a Multi-Star Related Graph [J]. Information Processing Letters, 1998, 68(6)：295-298.

[3]谭秋月.基于路的多重完全图相关图的生成树数目[J].曲阜师范大学学报：自然科学版，2012，38(3)：47-52. Tan Qiuyue. The Number of Spanning Trees of Multi-Complete Related Graphs Based on Paths[J]. Journal of Qufu Normal University：Natural Science，2012，38(3)：47-52.

[4]李晓明，黄振杰. 图中树的数目计算及其在网络可靠性中的作用[M]. 哈尔滨：哈尔滨工业大学出版社，1993：1-9. Li Xiaoming，Huang Zhenjie. The Number of Trees in Graph Calculation and Its Role in the Network Reliability [M]. Harbin：Harbin Institute of Technology Press，1993：1-9.

[5]谭秋月. 基于圈或路的多重星相关图的生成树数目[J].天津师范大学学报：自然科学版， 2013，33(1)：30-34. Tan Qiuyue. Number of Spanning Trees of Multi-Star Related Graphs Based on Cycles or Paths[J]. Journal of Tianjin Normal University：Natural Science Edition，2013，33(1)：30-34.

（责任编辑：邓光辉）

The Path-Based Enumeration of Spanning Trees of Multi-Complete Related Graphs

Tan Qiuyue
（Department of Mathematics and Computer，Wuyi University，Wuyishan Fujian 354300，China）

By means of Graph G labeling techniques, matrix and determinant computations, the complement-spanning-tree matrix theorem and inequalities computing etc., studies the number of spanning trees of the general situation of the path-based multi-complete related graphswhen m=2, 3, 4, 5, and a1, a2, …, amare arbitrary numbers, and gets relative counting formula.

multi-complete related graphs；spanning trees；complement-spanning-tree matrix theorem

O157.5

A

1673-9833(2014)05-0001-04

10.3969/j.issn.1673-9833.2014.05.001

2014-01-18

福建省教育厅科技基金资助项目（JK2012056），武夷学院一般基金资助项目（xq0933）

谭秋月（1980-），女，陕西杨凌人，武夷学院讲师，硕士，主要研究方向为图论和离散数学，E-mail：tqyspa@163.com