基于伴随方程和自由变形技术的跨声速机翼气动设计方法研究

白俊强，陈颂，华俊，孙智伟，黄江涛

（1．西北工业大学 航空学院，陕西 西安 710072；2．中国航空研究院，北京 100012；3．中国空气动力研究与发展中心，四川 绵阳 621000）

基于伴随方程和自由变形技术的跨声速机翼气动设计方法研究

白俊强1，陈颂1，华俊2，孙智伟1，黄江涛3

（1．西北工业大学 航空学院，陕西 西安 710072；2．中国航空研究院，北京 100012；3．中国空气动力研究与发展中心，四川 绵阳 621000）

将连续伴随方程法与自由变形技术（Eree Eorm Deform-FFD）相结合开展了跨声速机翼气动外形优化设计方法研究。采用Bernstein基函数建立了空间FFD参数化方法，并应用基于控制理论的连续伴随方程方法建立了目标函数对于待优化几何外形的梯度求解模式，将几何外形参数化方法、连续伴随方法以及CED数值模拟技术相结合，研究、构建了适合跨声速机翼的气动外形优化设计系统。利用该系统对ONERA M6机翼及某型民用客机机翼进行了气动减阻设计，算例验证表明该方法应用于跨声速机翼气动减阻设计效果明显，并且能较好的保持几何表面连续性和光滑性。

气动设计；伴随方程；自由变形；跨声速机翼

0 引 言

飞行器的气动设计直接影响了飞行器的气动性能以及飞行品质，是飞行器设计中的重要内容，一直以来，飞行器设计师以及航空学者们都在为研究开发高效的气动外形设计方法和设计工具而不断努力。

在气动设计方法中，Jameson提出的基于控制理论的连续伴随方程法［1］以其极高的效率成为当前国内外航空界广泛研究并应用的一种设计方法。该方法以偏微分方程系统的最优控制理论为基础，将待优化的气动外形几何边界作为控制函数，把流动控制方程作为约束条件在目标函数中引入，将约束问题转化为无约束问题，设计问题转化为控制问题。通过流场控制方程及其伴随方程同时求解目标函数相对于所有设计变量的梯度，每一次梯度求解的计算量只相当于约两倍的流场求解计算量［2］，并且几乎与设计变量个数的多少无关，应用这种方法可以大大提高气动外形设计的效率。1988年，Jameson等人首先将连续伴随方程法应用到了跨声速翼型气动优化设计中［3-6］，从此该方法在跨声速气动外形优化设计中获得了广泛的应用。该方法最初是基于结构网格推导的，1997年Anderson和Venkatakrishnan等人将其推广到了非结构网格上［7］。国内对于伴随方程法的研究开始较晚，乔志德、杨旭东等对结合控制理论与NS方程的气动反设计方法进行了研究［8］，唐智礼等应用特征不变量分析法处理了伴随方程的物面和远场边界条件，取得了较好效果［9］，陈作斌、周铸、黄勇等将连续伴随方程法结合B样条参数化方法发展了翼型气动优化方法［10-11］。

应用伴随方程法进行气动优化需要求解目标函数相对于设计变量的梯度，并且根据梯度信息进行设计变量的更新，从而得到新的几何外形，因此设计变量的选择对整个气动优化过程和结果有着决定性的影响。选择合适的设计变量不仅能大大减少优化设计时间，而且也是优化成功与否的关键［12］。在早期采用伴随方程法进行的气动外形设计工作中，每一个表面网格点都作为设计变量，在优化三维构型的情况下，设计变量可能达到成千上万个，并且容易造成气动外形不光顺的情况［12］。R．Hicks［13］和其他人则用一族形函数对设计空间进行了参数化，这族函数既可用以产生新的几何外形，也可用以对原有的几何外形产生扰动，但这些形函数存在的问题是不能形成完备的空间，有可能得不到设计问题的最优解。另一类方法是使用B样条控制点作为设计变量，虽然也可以减少设计变量的个数，还可以进行局部控制，但在实际中发现，当控制点较多时，B样条容易产生波动［12］，不适合于三维气动外形的设计。

自由变形方法（Free-Form Deform FFD）由Sederberg和Parry于1986年首次提出［14］，已经广泛应用在图形图像处理以及动画设计领域，近几年来开始在飞行器气动外形设计中得到初步应用。该方法具有变形空间大，不需要对初始外形进行拟合，操作简单等优点，并且可以很好的保持原有几何的连续性、光滑性，因此它可以作为一种应用于三维气动外形设计的参数化方法。F．Palacios等采用FFD方法对某超声速客机构型进行了气动优化设计，显著减小了激波阻力［15］，高正红、黄江涛［16］以及范召林、马晓永［17，18］等也分别采用FFD技术对翼型以及机翼进行了气动优化设计，取得了较好的效果。

本文采用自由变形方法对待优化几何外形进行参数化处理，选取FFD控制体顶点的位移作为设计变量，并应用基于三维Euler方程的连续伴随方程方法建立目标函数对设计变量的梯度求解模式，建立了针对跨声速机翼的气动设计系统，并对M6机翼以及某客机构型机翼进行了气动减阻设计，算例结果表明该方法优化效果明显，效率较高，并且能够较好的保持原有几何外形的连续性和光滑性。

1 流动控制方程及数值求解方法

本文采用三维Euler方程作为流场控制方程，其守恒形式如式（1-1）：

其中x1，x2，x3和u1，u2，u3为笛卡尔坐标系下的坐标和速度分量，守恒变量w和fi表示为：

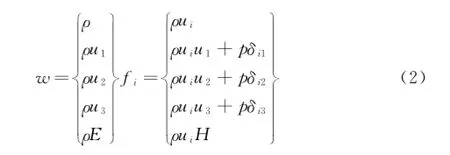
采用有限体积法求解Euler方程，空间离散格式为Jameson-Schmidt-Turkel（JST）中心格式，时间推进方法采用隐式欧拉法。

2 连续伴随方程法

气动设计问题是以求解外形变化对气动特能的影响为基础而进行的，为便于描述连续伴随方程法，选定计算坐标系（ξ1，ξ2，ξ3），一般情况下气动特性由目标函数表述为：

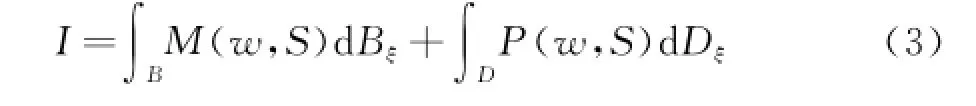
其中dBξ和dDξ分别为计算空间中的表面与空间积分单元，M与P取决于守恒变量w及计算空间矩阵S，分别表示目标函数表达式中的边界面积分部分和空间体积分部分。在满足流动控制方程约束条件下，气动外形的变化将导致流动变量变分δw与矩阵变分δS，因此目标函数的变化可表示为：

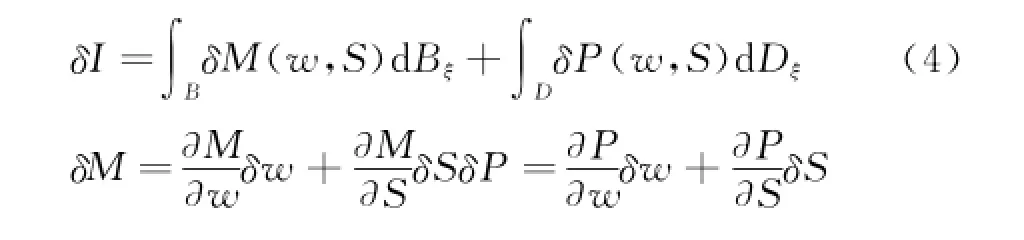
定常状态下，对应于气动外形变化的Euler方程可表述为：

其中Fi为流场守恒量，δFi也可写成与δw、δS相关的贡献，即：

引入共轭变量Ψ＝（Ψ1，Φ1，Φ2，Φ3，θ）T，在整个计算空间求积，则有：

假定Ψ可微，方程可进一步写成：

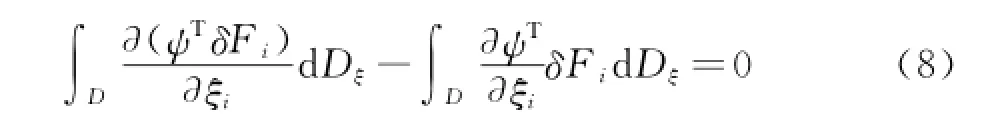
由高斯定理可得：

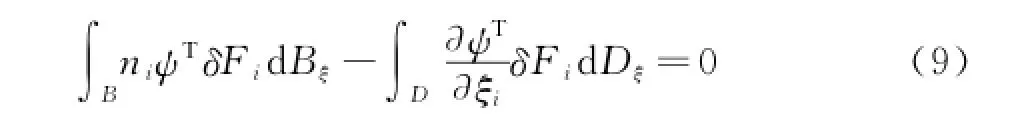
联系式（4）与式（5），把流动控制方程变分加入到目标函数变分中，则目标函数I的变分可写为：

由于假定共轭变量Ψ是任意一个可微函数，因而ψ就可选取为使δI中不再出现守恒变量变分δw的量，这样目标函数梯度就只与变换矩阵变分δS有关，而不必重新去求由于设计变量的扰动而引起的流场物理量变分δw。

把式（10）空间积分项中流动物理量变分δw的系数项组合在一起，则可得伴随方程：

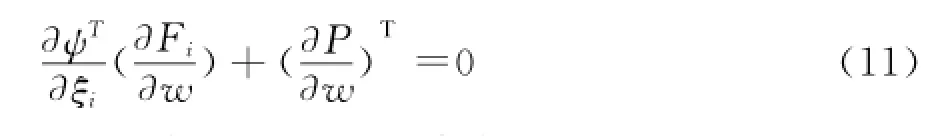
对应的伴随方程边界条件可由式（10）边界积分中流动物理量变分δw的系数项来得到，即：

这样目标函数变分项不再与流动变量变分δw相关，剩余项为目标函数变分δI的最终形式：

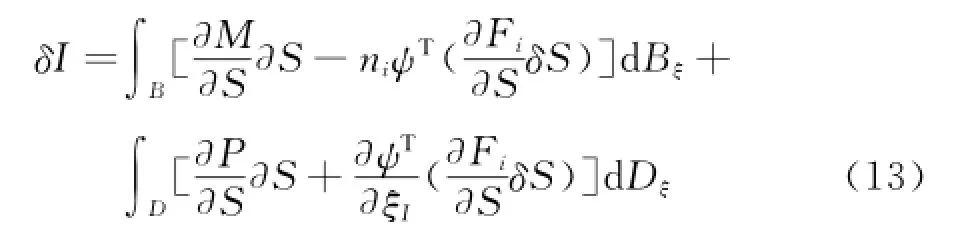
在气动减阻设计中，目标函数为［5］：

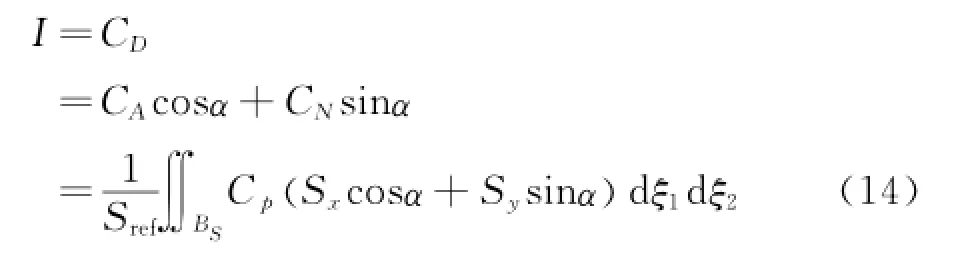
其中：Sx和Sy是两个坐标方向上的表面投影面积，Sref是参考面积，dξ1和dξ2是计算坐标系下的所求表面的微分。于是设计问题转换为了控制问题，控制函数即为几何外形。选择最优的几何外形以使目标函数I达到最小，在给定升力系数下额外的约束条件为：δCL＝0。目标函数的梯度最终可以写作［5］：

其中：ψT为共轭变量，Qij为相应的雅可比矩阵。

3 自由变形参数化方法

自由变形方法（Free Form Deform-FFD）由Sederberg和Parry于1986年首次提出［14］，该方法仿照弹性物体受外力后发生相应的变形这一物理现象，将研究对象置于控制体当中，给控制体施加外力，则控制体内的所有几何发生相应变形，处于其中的研究对象形状也即发生变化；这一过程用数学关系表示即为：移动控制体中的控制点（这使得控制体形状改变，模仿了控制体受力后形状改变的现象），研究对象的每一点随控制顶点的移动，按照某一函数关系相应的移动，其几何形状随之改变。

本文采用六面体形状控制体，以控制体的三条边的方向建立局部坐标系，S、T、U是局部坐标系轴矢量，沿三个边的方向分别均匀布置l＋1、m＋1、n＋1个控制节点，控制点沿各边均匀分布，令Pi，j，k为控制点的全局坐标值；

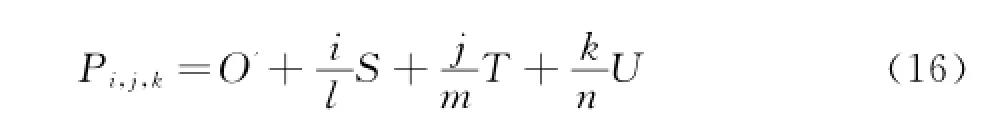
其中，i＝0，1，…l；j＝0，1，…m；k＝0，1，…n。

令X0（O）为局部坐标系的原点在全局坐标系下的坐标；X是控制框架内任意一点的全局坐标，s、t、u分别为该点的局部坐标，0≤s，t，u≤1，则有：

其中：

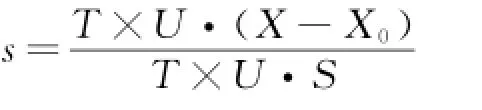
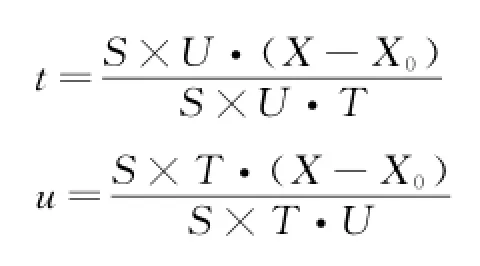
本文采用Bernstein基函数建立控制体各顶点坐标与控制体内任意一点坐标之间的映射关系，

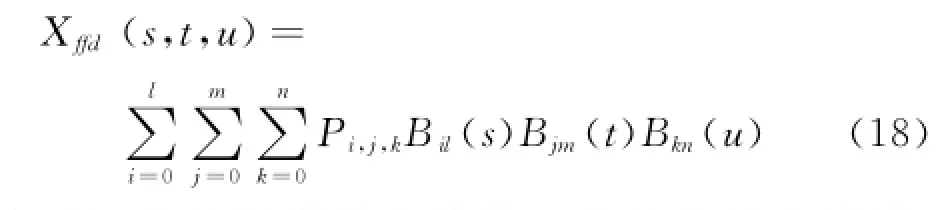
其中：Xffd为控制框架内任意一点的全局坐标值；Pi，j，k为控制点的全局坐标值；Bil（s）、Bjm（t）、Bkm（u）分别为l、m、n次Bernstein多项式基函数；s、t、u分别为该点在局部坐标系O’STU中沿S、T、U方向的坐标值。当控制点的位置变化，Pi，j，k亦随之改变，导致控制体内任意一点坐标受此扰动后也发生改变。

当构造较为复杂的形体时，需要对变形对象施加两个或者更多的FFD变形，对于局部变形来说，为保持切矢以及曲率连续，对FFD空间拓扑以及控制要求更严格。对于局部参数为（v，m）的曲面可以表示为：

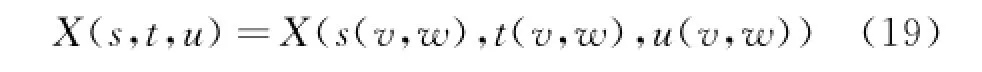
任意FFD空间组合X0（s，t，u），X1（s，t，u）共享边界s0＝s1＝0，曲面变形后沿v，m方向一阶导矢为：

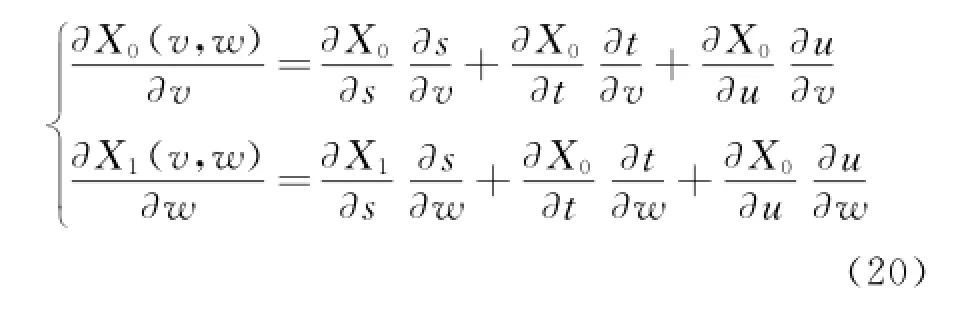
4 FFD技术与连续伴随方程相结合的气动外形优化设计系统

为了克服以每一个网格点作为设计变量而造成的设计外形不光顺或者采用B样条参数化方法造成的波动等问题，本文将基于连续伴随方程的梯度求解模式与FFD方法相结合，针对跨声速机翼外形进行了气动减阻设计。

采用自由变形参数化方法将待优化几何外形进行参数化，以每个FFD控制顶点的位移作为设计变量，求解目标函数相对于设计变量的梯度。根据梯度信息更新设计变量，在设计变量的值更新后，采用FFD方法进行几何外形的变形，不需要进行网格光顺即可保持原有几何属性如连续性、光滑性等。目标函数相对于每个设计变量的梯度可以通过式（22）求得，其中为FFD控制顶点的位置改变：

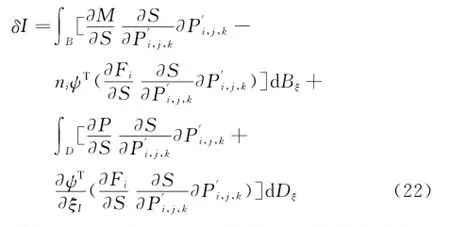
采用FFD方法可以处理机翼气动外形设计在工程实际应用中需要考虑的容积约束问题。由FFD变形所引起的任意实体微元的变化可由FFD的雅可比行列式得到，若FFD变形由下式给出：

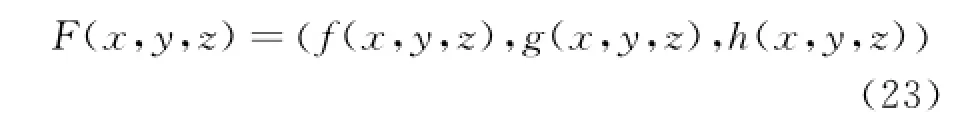
则其雅可比行列式为：

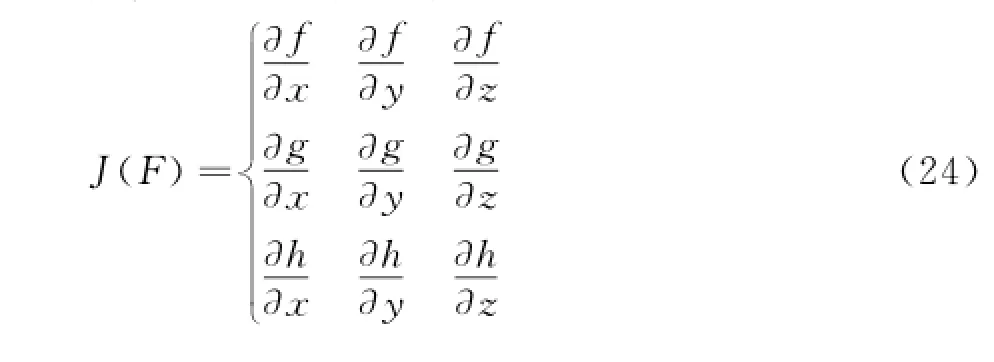
若变形前微元的体积为dxdydz，则变形后此微元的体积变为J（E）dxdydz，变形后整个实体的体积是雅可比行列式在变形前实体上的三重积分，因此，若已知J（E）在变形区域上的上下界，当J（E）由三变量的Bernstein多项式表示时，则可以估计出其上下界。此时，多项式的最大和最小系数即是体积变化的上下界［19］。

结合FFD技术和连续伴随方程法构建机翼气动外形优化设计系统，优化流程如图1所示。以数值计算中的表面网格点定义待优化的几何外形，首先在待优化外形周围布置FFD控制体，并求解其在控制体中的局部坐标（即式（18）中的s、t、u），建立从几何空间到局部空间的映射关系。以FFD控制顶点的位移作为设计变量，实现对待优化外形的几何参数化。而后由CED求解器采用三维欧拉方程（式（1））对初始外形流场进行数值计算，待计算收敛后，采用空间流场信息作为输入数据，求解连续伴随方程（式（11）），得到优化目标函数对于设计变量的梯度，根据梯度信息采用优化算法更新设计变量的值，由新的设计变量应用自由变形方法对待优化几何外形进行变形，并且根据变形后的FFD控制体估算机翼的容积，若容积减小则按照外点罚函数方法进行惩罚。根据变形后的几何外形表面网格，采用动网格方法进行相应的空间网格变形，生成与新的外形相对应的空间网格。而后对新的外形进行流场数值计算，并判断优化是否完成，如未完成，继续求解梯度并且更新设计变量直至优化收敛。本文中动网格技术采用了Torsional Spring动网格方法［20］。

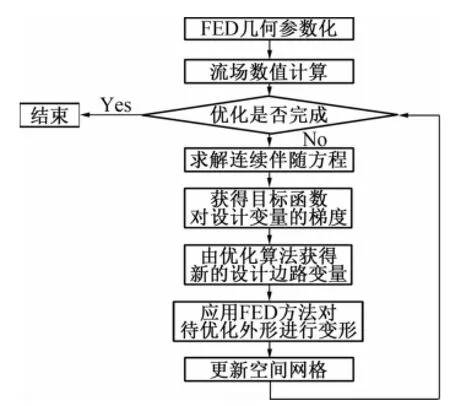
图1 气动设计方法流程图Fig.1 Flow chart of aerodynamic design based on continuous adjoint method

5 验证算例

本文对于ONERA M6机翼以及某型民用客机机翼外形进行了气动减阻设计。

5.1 ONERA M6机翼气动减阻设计

在M6机翼周围建立FFD控制框，如图2所示FFD控制点共计126个，控制点沿各边均匀分布。以消除机翼上表面明显的λ形激波为气动减阻设计的主要目的，把控制体上表面各控制点垂直水平面方向的位移作为设计变量，则设计变量共63个。约束条件为升力系数以及机翼内部容积相对于原始构型不减小，优化算法为最速下降法。整个优化过程共调用CED求解器及伴随方程求解器各23次，共花费计算机机时2小时（8核PC机），从初始外形得到设计外形。由于FFD方法的特性，优化后的几何外形保持了原有的连续性和光滑性。优化前后机翼几何外形以及FFD控制点分布的对比如图2所示。设计前后表面压力分布对比如图3所示。从压力分布的对比可见，经过气动优化设计，机翼上表面的激波显著减弱，优化前后机翼阻力系数的对比如表1所示。优化设计的收敛过程如图4所示。经过优化设计后机翼阻力系数相比原始构型从0．0123减小到0．0093，相比原始构型阻力减小约24．39%，升阻比从21．38提高到28．17，相比原始构型提高了31．76%，同时升力系数下降了0．001，相对容积只减少了1．3%。

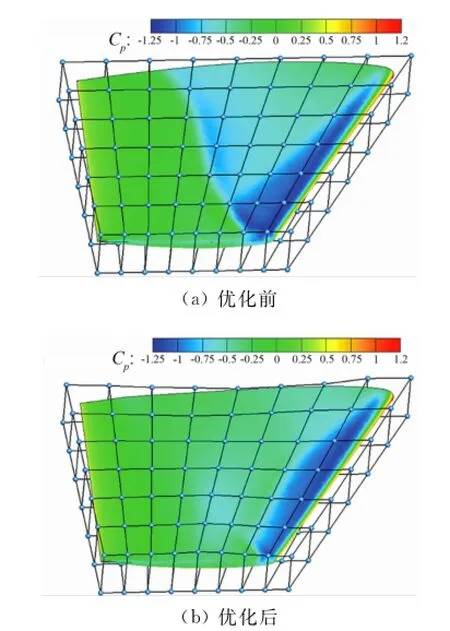
图2 M6机翼优化前后表面压力分布以及控制点分布对比Fig.2 Surface pressuredistribution and thedistribution of control points of M6 wing before and after optimization

图3 M6机翼优化前后表面压力分布对比Fig.3 Surface pressure isobardistribution of M6 wing before and after optimization

图4 M6机翼优化收敛历史Fig.4 Convergence history of thedesign of M6

表1 M6机翼优化前后气动特性对比Table 1 Comparison of aerodynamic performance of the M6 wing before and after opimization

5.2 某型民用客机机翼气动减阻设计

针对某民用客机机翼外形进行了第二个验证算例，机翼几何外形以及FFD控制顶点分布如图5所示，FFD控制点共198个，取FFD控制体上表面的控制顶点垂直水平面的位移量作为设计变量，则设计变量共计99个。约束条件为升力系数和相对容积相比原始构型不减小，优化算法为最速下降法。整个优化过程共调用CED求解器及伴随方程求解器各40次，共花费计算机机时20小时（8核PC机）。优化后机翼表面压力分布以及FFD控制顶点分布如图6所示。优化前后机翼的气动特性参数对比如表2所示，优化后机翼阻力系数从0．0261减小到0．0212，优化后阻力相对原始构型减小18．77%，升阻比从20．07提高到了25．94，提高29．3%，同时优化前后相对容积只减小了1．9%，升力系数不变，并且优化后机翼表面几何外形很好的保持了原有外形的连续性和光滑性。优化前后机翼表面压力分布对比如图7、图8所示，优化设计的收敛过程如图9所示。可见经过设计之后，机翼内外翼的激波均明显减弱，减阻效果显著。

图5 某型客机初始机翼表面压力分布以及控制点分布Fig.5 Initial surface pressure distribution and the distribution of control points

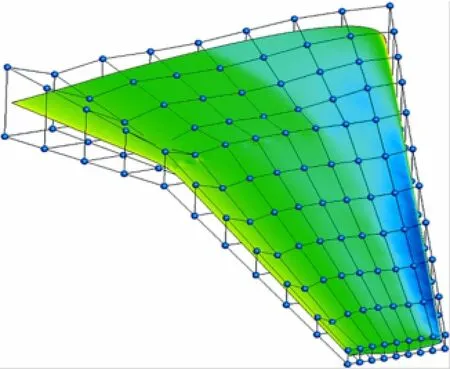
图6 某型客机优化后机翼表面压力分布以及控制点分布Fig.6 Optimum surface pressure distribution and the distribution of control points

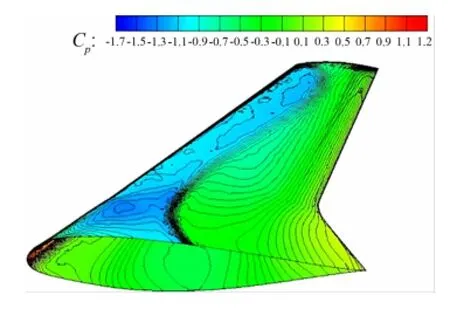
图7 某型客机初始机翼表面压力分布Fig.7 Initial surface pressure distribution of civil jet wing

图8 某型客机优化后机翼表面压力分布Fig.8 Optimum surface pressure distribution of wing

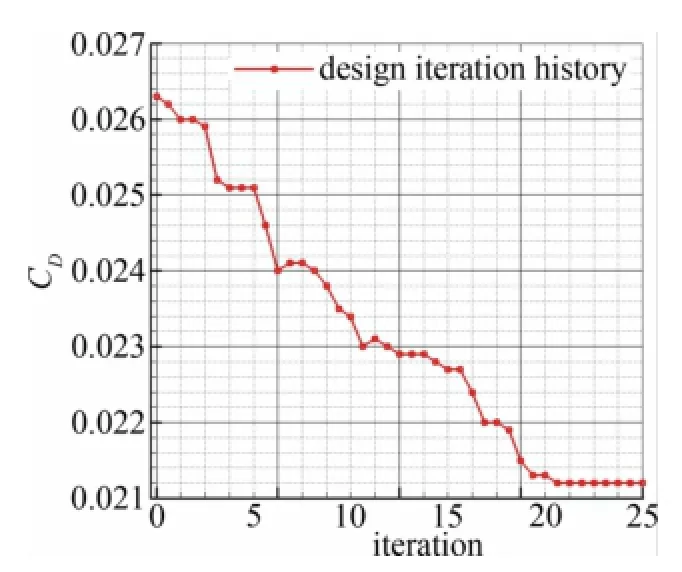
图9 某型客机优化后机翼表面压力分布Fig.9 Convergence history of the design of M6

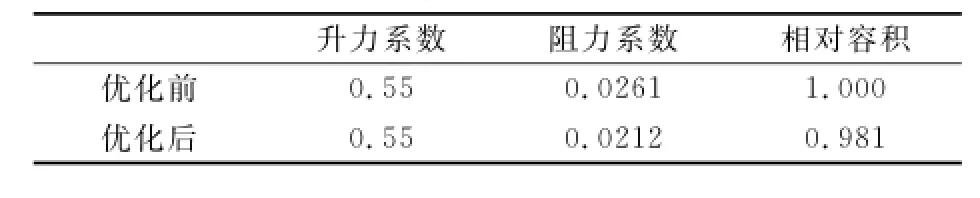
表2 某型客机机翼优化前后气动特性对比Table 2 Comparison of aerodynamic performance of the aero transport’s wing before and after optimization

6 结 论

（1）将FFD技术与连续伴随方程法相结合，以FFD控制点位移代替每个表面网格点的位移作为设计变量，可以使设计外形很好的保持原有外形的几何连续和光滑性。

（2）采用FFD技术进行气动优化设计，可以有效估计优化过程中所产生的每个结果的几何容积。

（3）两个验证算例中构型的气动减阻设计在8核PC机的计算平台下均在一天之内完成（分别为3小时和20小时），从设计结果可见，FFD技术和连续伴随方程相结合的跨声速机翼气动优化设计系统对于跨声速机翼的气动减阻设计效果明显且效率较高。

［1］JAMESON A．Aerodynamicdesign via control theory［J］．Journal of Scientific Computing，1988，3：233-260．

［2］ WIDHALM M，RONZHEIMER A，HEPPERLE M．Comparison between gradient free and adjoint based aerodynamic optimization of a flying wing transport aircraft in the preliminarydesign［R］．AIAA 2007-4060．

［3］JAMESON A．Optimum aerodynamicdesign using CED and control theory［R］．AIAA 95-1729-CP，1995．

［4］JAMESON A．Control theory based airfoildesign using Euler equation［R］．AIAA 94-472-CP，1994．

［5］REUTHER J，JAMESON A．Control theory based airfoildesign for potential flow and a finite volumediscretization［R］．AIAA 91-499，1994．

［6］REUTHER J，JAMESON A．Aerodynamic shape optimization of complex aircraft configuration via an adjoint formulation［R］．AIAA 96-0094．1996．

［7］ANDERSON W K，VENKATAKRISHNAN V．Aerodynamicdesign optimization on unstructured grid with a continuous adjoint formulation［R］．AIAA 97-0643，1997．

［8］YANG X D，QIAO Z D，ZHU B．Aerodynamicdesign method based on control theory and Navier-Stokes equations［J］．ACTA Aerodynamica Sinica，2005，23（1）：46-52．（in Chinese）

杨旭东，乔志德，朱兵．基于控制理论和NS方程的气动设计方法研究［J］．空气动力学学报，2005，23（1）：46-52．

［9］TANG Z L，HUANG M K．Control theory based airfoildesign using Euler equations［J］．ACTA Aerod ynamica Sinica，2001，19（3）：262-270．（in Chinese）

唐智礼，黄明恪．基于控制理论的Euler方程翼型减阻优化设计［J］．空气动力学学报，2001，19（3）：262-270．

［10］HUANG Y，CHEN Z B，LIU G．An investigation of aerodynamic optimizationdesign for airfoil based on adjoint formulation［J］．ACTA Aerod ynamica Sinica，1999，17（04）：413-422．（in Chinese）

黄勇，陈作斌，刘刚．基于伴随方程的翼型数值优化设计方法研究［J］．空气动力学学报，1999，17（04）：413-422．

［11］ZHOU Z，CHEN Z B．Airfoil aerodynamicdesign and optimization based on Navier-Stokes equations［J］．ACTA Aerodynamica Sinica，2002，20（02）：141-149

周铸，陈作斌．基于N-S方程的翼型气动优化设计［J］．空气动力学学报，2002，20（02）：141-149

［12］XIONG J T．Aerodynamic shape optimizationdesign based on adjoint method and Navier-Stokes equation［D］．Xi′an：Northwestern Polytechnical University．2007

熊俊涛．基于伴随方法和Navier-Stokes方程的气动优化设计［D］．西安：西北工业大学，2007

［13］HICKS R M，HENNE P A．Wingdesign by numerical optimization［R］．AIAA 79-0080．1979．

［14］SCOTT T S，PARRY R．Eree-formdeformation of solid geometric models［J］．Computer Graphics，86，20（4）：150-161．（SIGGRAPH 86．）

［15］PALACIOS E，ALONSO J J，COLONO M，et al．Adjointbased method for supersonic aircraftdesign using equivalent areadistribution［R］．AIAA 2012-0269，2012．

［16］HUANG J T，GAO Z H，BAIJ Q，et al．Laminar airfoil aerodynamic shape optimizationdesign based on Delaunay graph mapping and FFD technique［J］．Acta Aeronautica et Astronautica，2012，33（10）：1817-1826

黄江涛，高正红，白俊强，等．应用Delaunay图映射与FFD技术的层流翼型气动优化设计［J］．航空学报，2012，33（10）：1817-1826．

［17］MA X Y，WU W H，EAN Z L．Ereedeformation method of wing based on NURBS［J］．Journal of Sichuan University（Engineering Science Edition），2010，42（增2）：195-197．

马晓永，吴文华，范召林．基于NURBS的机翼自由变形方法［J］．四川大学学报，2010，42（增2）：195-197．

［18］MA X Y，EAN Z L，WU W H，et al．Aerodynamic shape optimization based on FFD［C］．13rdSystem Simulation Technology＆Application，2011．

马晓永，范召林，吴文华，等．基于FFD技术的机翼气动外形优化仿真［C］．第13届中国系统仿真技术及其应用学术年会（13卷），2011．

［19］朱心雄．自由曲线曲面造型技术［M］．北京：科学出版社，2000．

［20］DEGAND C，EARHAT C．A three-dimensional torsional spring analogy method for unstructureddynamic meshes［J］．Computers&Structures，2002，80（3）：305-316．

Transonic wing aerodynamicdesign based on
continuous adjoint method and free formdeform technique

BAI Junqiang1，CHEN Song1，HUA Jun2，SUN Zhiwei1，HUANG Jiangtao1
（1．Northwest Polytechnical University，Xi’an 710072，China；2．China Aeronautical Establishment，Beijing 100012，China）

The approach of transonic wing aerodynamicdesign based on the combination of continuous adjoint method with free formdeform（FFD）technique has been presented．Bernstein basis function has been chosen to establish the FFD parameterization of arbitrary spatial property to overcome thedisadvantages ofdiscontinuity or unsmoothness by the bump function method or the B-spline approach．Besides，the scheme to compute the sensitivity of aerodynamic objective function respecting to geometrical shape has been established using the continuous adjoint method based on control theory，in which the sensitivity computation of all thedesign variables would cost one flow field computation and one adjoint field computation．Combinedwith torsional spring meshdeformation technique，FFD geometric parameterization，continuous adjoint method and computational fluiddynamics have been integrated to establish adesign system for transonic wing aerodynamic configuration aimmed atdrag reduction，which is good at both efficiency and robustness．This system has been testified with optimizationdesign cases of ONERA M6 wing and a typical large civil jet wing，the results of which have shown that this method is of good feasibility and efficiency in aerodynamic optimizationdesign fordrag reduction．Moreover，the results have shown that this method is of good capability of conserving the geometry continuity and smoothness．

aerodynamicdesign；continuous adjoint method；free formdeform；transonic wing

V211.3；TP273

Adoi：10.7638／kqdlxxb-2012.0198

0258-1825（2014）06-0820-08

2012-12-03；

2013-03-10

973计划大型客机减阻机理和方法研究（2014CB744804）

白俊强（1970-），男，河南新乡人，教授，主要研究方向：飞行器设计．

白俊强，陈颂，华俊，等．基于伴随方程和自由变形技术的跨声速机翼气动设计方法研究［J］．空气动力学学报，2014，32（6）：820-826．

10．7638／kqdlxxb-2012．0198 BAI J Q，CHEN S，HUA J，et al．Transonic wing aerodynamicdesign based on continuous adjoint method and free formdeform technique［J］．ACTA Aerodynamica Sinica，2014，32（6）：820-826．