对牛顿第二定律F = ma的理解

聂春明

一、矢量性

F = ma是一个矢量式，力和加速度都是矢量，物体的加速度的方向由物体所受合外力的方向决定。已知F的方向，可推知a的方向，反之亦然。加速度a的方向与合外力F的方向始终相同。

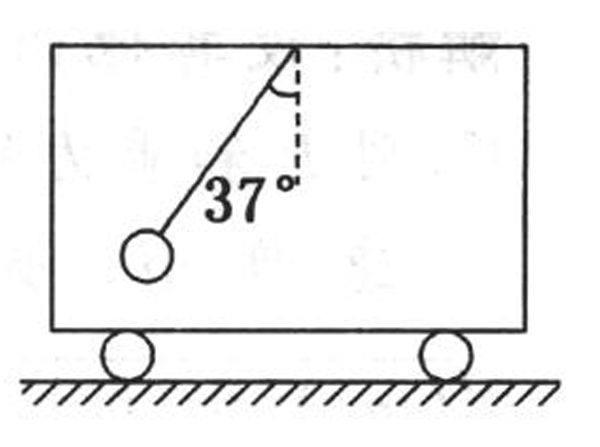
例：如图所示，沿水平方向做匀变速直线运动的车厢中，悬挂小球的悬线偏离竖直方向37°角，球和车厢相对静止，球的质量为1kg。求：车厢运动的加速度并说明车厢的运动情况。

小球和车厢相对静止，它们的加速度相同。以小球为研究对象，对小球进行受力分析如图所示，小球所受合力F合 = mgtan37°，由牛顿第二定律得小球的加速度为，加速度方向向右。

车厢的加速度与小球相同，车厢做的是向右的匀加速度运动或向左的匀减速运动。

二、瞬时性

物体的加速度a与合外力F是瞬时对应关系：F为0时，则a为0；F不为0时，则a不为0；F改变，则a立即改变。a和F同时存在，同时消失，同时改变。因此它适合解决物体在某一时刻或某一位置时力和加速度的关系问题。

例：如图所示，天花板上用细绳吊起两个用轻弹簧相连的质量相同的小球，两个小球均保持静止，当突然剪断细绳时，上面小球A与下面小球B的加速度为（ ）

A.aA = g，aB = g B.aA = g，aB = 0

C.aA = 2g，aB = 0 D.aA = 0

剪断瞬间对A来讲绳子拉力立即消失，而弹簧中的弹力不能突变，A只受弹簧弹力与重力，对B来讲受力不变。分别以A、B为研究对象，做剪断和剪断时的受力分析。剪断前A、B静止，如图甲所示，A球受绳子的拉力T、重力mg和弹簧弹力F的作用。B球受重力mg和弹簧弹力F′（大小等于F）两个力的作用。

A球：T – mg – F = 0

B球：F ′ – mg = 0

联立两式解得T = 2mg，F ′ = F = mg。

剪断时，A球受两个力，因为绳子剪断瞬间拉力突然消失，而弹簧有形变，瞬间形状不可改变，弹力还存在，如图乙所示，A球受重力mg、弹簧弹力F。同理B球受重力mg和弹力F ′ 。

A球：mg + F = maA ，B球：F ′ – mg = maB。

解得aA = 2g（方向向下），aB = 0。故选C项。

三、独立性

（1）作用在物体上的各个力各自产生相应的加速度，不因其他力的作用而改变。物体的加速度是合外力产生的，又可以理解为各力产生加速度的矢量和：，，…，a等于a1，a2，…的矢量和。

（2）牛顿第二定律的分量式，根据力的独立作用原理，运用正交分解，x轴方向的合力产生ax ，y轴方向的合力产生ay ，所以F = ma可以用其他两个分量来代替：即。

特别指出的是：若F为物体所受的合外力，那么a表示物体的实际加速度；若F为物体所受的某一个方向上的力，那么a表示物体在该方向上的分加速度；若F为物体所受的若干力中的某一个力，那么a仅表示该力产生的加速度。

例：如图甲所示，质量为m的人站在自动扶梯上，扶梯正以加速度a向上做减速运动，a与水平方向的夹角为，求人所受的支持力和摩擦力。

以人为研究对象，他站在减速上升的电梯上，受到竖直向下的重力mg、竖直向上的支持力FN ，还受到水平方向的静摩擦力f，由于物体斜向下的加速度有个水平向左的分量，故可判断静摩擦力的方向水平向左。人的受力如图乙所示，并将加速度分解为水平加速度ax和竖直加速度ay，则，；由牛顿第二定律得：，，求得：，。

四、同体性

牛顿第二定律关系式：F合=ma中的三个物理量是对同一物体或同一系统而言的，分析物体受力情况和认定加速时切不可张冠李戴。

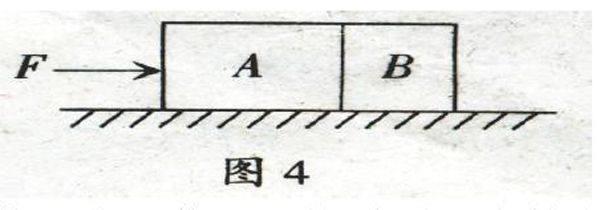
例：如图所示，质量为2m的物体A与水平地面的摩擦可忽略不计，质量为m地物块B与地面间的动摩擦因数为μ，在已知水平推力F作用下，A、B一起做加速運动，求A B间的作用力。

先把A、B看作一个整体，系统受到的合外力为，得系统的加速度为，再对物体B分析，由牛顿第二定律得：，解得：。

参考文献：

[1]《普通高中课程标准实验教科书·物理必修1》.

[2]《全程设计高中新课堂同步课堂》.

[3]《鼎尖教案》人教版，物理必修1.