硕士研究生复试总成绩分析及招生规模研究
2014-04-27李淑君王建梅孟文俊
李淑君,王建梅,孟文俊,王 尧
(太原科技大学机械工程学院,山西 太原 030024)
随着我国教育改革的不断调整和优化,研究生教育出现了跨越式发展[1],招生规模逐年增长。如何在扩招的同时保证生源质量,就成为研究生招生工作的首要问题。硕士是介于学士及博士之间的研究生学位,要注重培养学生对问题的研究和分析能力,特别是对所属学科的科研能力。因此,在硕士研究生招生工作中,能否保证招收到优质生源,直接关系到研究生的培养质量。
诸多文献已对硕士研究生招生工作做过大量研究。比如,余刚等运用统计学及教育测量学方法,探讨了军医进修学院硕士研究生入学考试课程的总体成绩与各科成绩的分布规律[2];曾文艺等利用模糊聚类分析方法对研究生考生排名录取问题进行了数学探讨[3];刘海燕等通过多元回归和逐步回归分析方法,对研究生入学考试成绩与后续主干课程之间的影响程度进行了分析[4]。上述文献都不同程度地对硕士研究生招生工作的入学考试成绩进行了限定性研究,但忽略了面试工作定量化在招生工作中的重要性,极可能导致优秀生源的流失与招生质量的下降。
在保证考生及时、有效和充分获取研究生招生调剂信息的情况下[5],本文结合太原科技大学机械工程学院近三年硕士研究生招生工作中积累的相关数据,对已录取的371名考生(有部分学生去宁波理工学院培养)复试总成绩中的入学考试成绩与复试成绩分别进行了数据归一化处理,并进行了关联性分析,之后根据本学院学科特色建立了招生规模控制模型,以确保硕士研究生的培养质量。
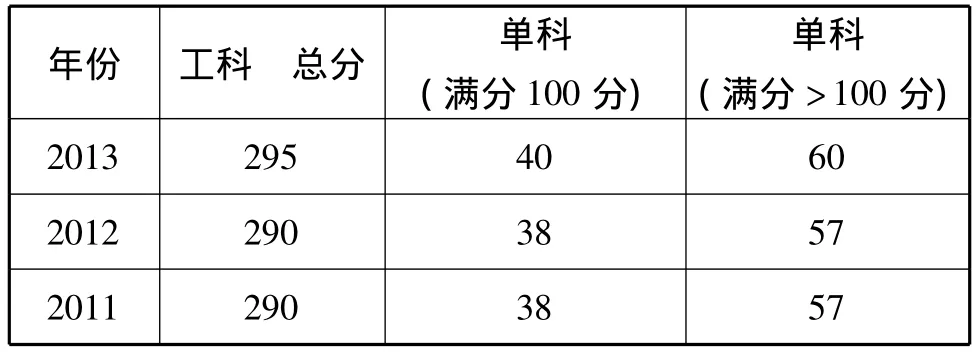
表1 近三年硕士研究生考生复试国家线要求
一、初试成绩分析
(一)考生入学考试成绩分布
教育部公布的近三年全国硕士研究生招生考试考生进入复试的初试基本成绩要求见表1所示。从表1可以反映出,近三年题目难易程度适中。
用成绩分布图表可以直观地说明大规模考试成绩的分布状态[6]。我院近三年硕士研究生入学考试成绩统计分析结果见表2所示。
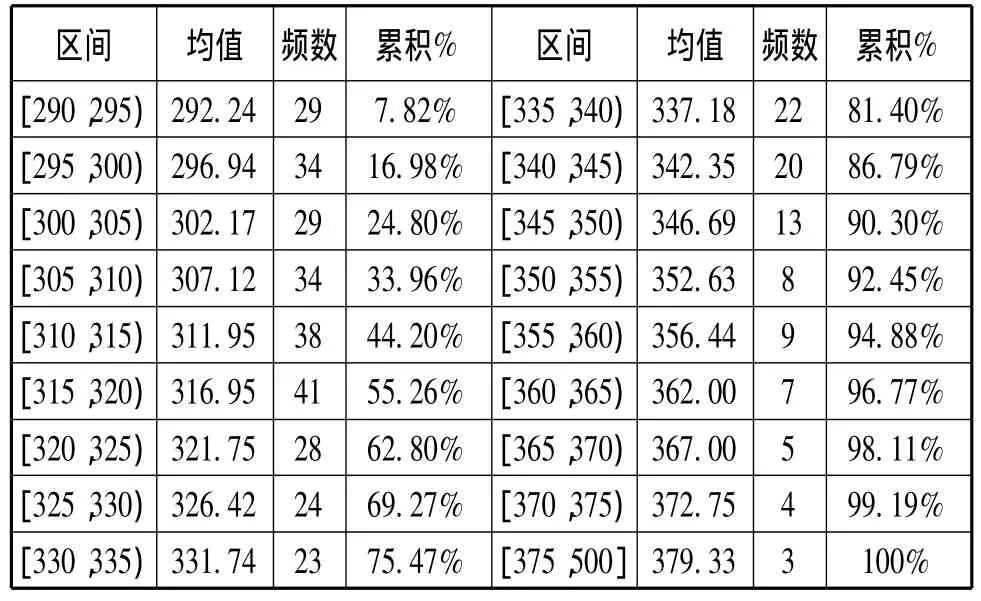
表2 近三年我院录取研究生入学考试成绩频数表
(二)考生入学考试成绩频数及累计人数百分比分布
以各区间均值作为横坐标,频数作为纵坐标,利用Origin Pro8绘制对应的考生入学成绩频数分布曲线,并对其进行Guass正态拟合,如图1所示。

图1 硕士研究生入学考试成绩分布曲线
图1中显示的考生入学考试成绩分布曲线,其正态均值μ=309.15,说明考生入学考试成绩分布的集中趋势在310分左右,决定了录取考生的初试成绩分布曲线的位置;而标准差σ=25.32,说明录取考生初试成绩分布的离散程度,同时可明显地表征在μ±σ处有拐点,结合表2可知:落入此区间的概率为75.47%。近三年考生入学考试成绩累计人数百分比随各区间均值的分布曲线,如图2所示。
对图2分析可以看出:2011年考生入学考试成绩分布曲线与2012年、2013年相比明显向左移,2012年较2013年微向左移,说明2011年考生总体成绩比2012年、2013年略低。而表1反映试题难度相当,那么图形反映2012年、2013年应试考生水平普遍较高,每年考生质量有所提高,但同时亦反映出2011年录取考生高分人数比例相比后两年要高。
上述分析要求我院招生工作相关人员,尤其在招生调剂初期,一定要及时抓好优秀生源,对调剂信息系统中有意向调剂的考生要及时回复是否复试,切勿因为时间拖延而使相对优秀生源流失。

图2 近三年考生入学考试成绩累计人数百分比分布图
二、复试总成绩分析
(一)关联分析模型
在招生复试工作中,为确保我院硕士研究生生源质量和招生工作顺利进行,按照教育部相关招生录取工作的通知以及山西省招生考试管理中心对研究生复试工作的要求,基于研究生学院制定的学校总体招生方案,每年都将制定学院具体的复试细则。复试细则中对考生复试总成绩的算法要求为:
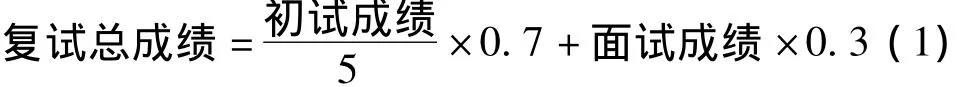
其中,面试成绩由专业课笔试成绩和综合面试成绩两部分组成,所占的比例分别为60%、40%,综合面试成绩主要包括英语听说能力测试和专业面试(考核基础知识、专业知识、相关技能等)。
为了掌握入学考试成绩和复试成绩对复试总成绩之间的不确定关联,以各因素的样本数据为依据,用灰色关联度来描述因素间关系的强弱、大小和次序[7]。由于各因素的样本数据属于不同数量级大小的数据,需要对各因素的样本数据进行数据归一化处理,采用方法为最大最小值法[8],目的是将样本数据归一化到[0,1]范围内。
数据归一化计算公式为:

式中:x(n)——样本数据数列;
x(k)——样本数列中第k个数据;
y(k)——样本第k个数据归一化对应的数据;
max(x(n))、min(x(n))——样本数据数列中的最大值、最小值。
由式(2)确定参考序列x0和比较序列xi,即:


式中:i——代表关联因素个数,1≤i≤n;m——代表各因素序列中的元素个数。
在第k时刻(或者第k点)xi序列对于x0序列的关联系数ζi(k)计算公式为:
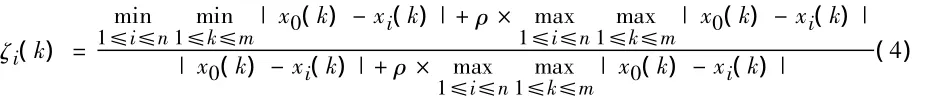
式中:ρ——分辨系数[9],取值为 ρ∈[0,1],人为给定,ρ越小,分辨率越大。通常取ρ=0.5。
确定xi对x0的关联度r(x0,xi)为:

由式(5)可以看出,关联度r(x0,xi)是ζi(k)的平均值。也就是说关联度系数很多,信息分散,其每个值代表某一个指标两个数列的关联程度,对所有关联系数取平均值是为了表明两个数列总体关联程度。依据r(x0,xi)的大小可以排出各因素序列间影响程度的大小顺序,数值较大的,表明此因素是发展趋势最接近的因素。
(二)数据计算
将已录取的371名考生复试总成绩作为参考序列x0,入学考试成绩与复试成绩分别作为比较序列x1、x2,并对各序列数据进行归一化处理,再根据式(5)计算比较序列与参考序列之间的关联度r1、r2,之后列出关联序。式(5)计算结果为:x1对x0的关联系数,r1=0.48;x2对 x0的关联系数,r2=0.69。即x2是与x0发展趋势最接近的因素,关联序为r2>r1。由此可见:
1.面试工作定量化在招生工作中非常重要,不能单纯从入学考试成绩来判断一个学生的优劣。
2.我院根据专业特色划分了硕士研究生考生复试小组,如果考生拟报专业或调剂专业与所在复试小组学科不一致,极有可能导致复试结果不理想,也间接突显面试工作在选拔优秀人才方面的重要性。
3.研究生教育是高层次教育,是将本科毕业生(或同等学力)中的优秀考生选拔出来加以培养。因此,对硕士研究生复试总成绩进行全面综合分析,可以较准确地衡量学生的真实水平,有利于我院把好研究生入学质量关。
三、招生规模控制模型
2005年我国在校研究生规模突破100万人,成为继美国之后在校研究生数位居世界第二的国家,标志着我国进入研究生教育大国前列[10]。但是规模激增引起重重矛盾,教育培养质量受到各界质疑,相关研究生招生规模的建模与预测以及合理的招生分配问题研究倍受关注[11-12]。在做好研究生招生工作的同时,各个高校能否为国家培养大量高层次、高质量人才问题显得尤为重要。
作为省部共建重点特色学科类高校,我院结合学科特色,整合教育资源、研究经费、师资队伍、教学和实验设施,在合理制定研究生招生计划的同时,提出了招生规模控制模型,旨在不断提升复合型、应用型人才的培养质量,增强学校服务地方的发展能力。
(一)模型建立
由于招生名额有限,为了更好地协调导师与招生名额的矛盾,学院制定了招生模型的建立原则:
1.近三年无课题的教授限招1名(包括多个方向),如果有国家、省基金项目的教授,可增加1名。
2.跨学院招收硕士研究生的导师限招1名(包括多个方向)。
3.副教授(包含新导师)限招1名(包括多个方向),如果有国家、省基金项目的导师,可增加1名。
4.博士生导师可适当增加1名,其他导师根据学生报名情况适当调配。
设我院有硕士研究生导师N名,教授x名,其中博士生导师x1名,有国家、省基金项目教授x2名;副教授y名,其中有国家、省基金项目副教授y1名;跨学院导师z名,则招生总数f的表达式为:
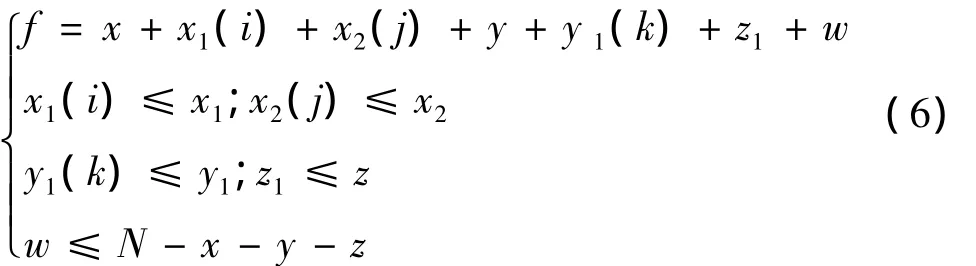
式中:x1(i)——博士生导师增加的名额;
x2(j)——教授中有国家、省基金项目的导师增加的名额;
y1(k)——副教授中有国家、省基金项目的导师增加的名额;
z1——跨学院导师愿意招研究生的人数;
w——其他导师愿意招研究生的人数。
从式(6)看出,招生总数f在模型建立原则下有个极大值,可以看作是一个线性规划问题。很显然,如果招生计划大于该极大值,那么此原则下的招生规模模型将不具有可控性。结合我院近三年招生实际情况,此模型在理论上可以保证每个硕士生导师有足够的精力与能力辅导硕士研究生的科研学习。
(二)模型计算与分析
我院师资条件及相关计算参数见表3所示。
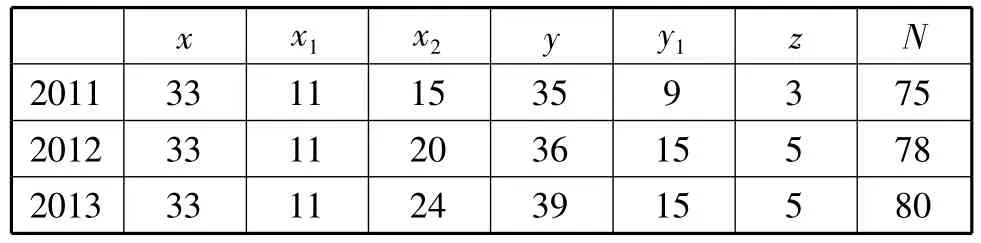
表3 我院硕士生导师相关参数
假定我院每位硕士生导师工作热情高、积极负责、都想带到尽可能多而优秀的学生,那么按照模型建立原则,只要符合要求,就可以增加名额。我院实际招生人数f'(包括推免生)与招生规模控制模型下的招生总数f结果比较见表4。
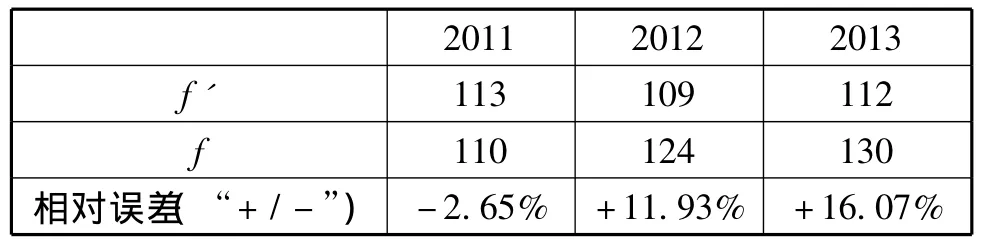
表4 招生数量结果分析
1.表4中相对误差随着年份增加逐渐增大,说明所建立的招生规模控制模型,越来越有活力,相对于硕士研究生导师来说呈现“供不应求”,能够间接保证每年所招硕士研究生的培养质量。
2.表4中2011年相对误差为负,2012年增幅较大。结合表3数据,不难发现2011年在研国家级与省级项目的导师偏少(多数已经提交结题评审);2012年导师进行项目申请并获得者明显增加,说明我院导师具备发展的科研前景和较高的科研能力,也反映出导师对学生认真负责的务实态度,如果想多招学生就得持续提升自身发展素质。
3.表4中随着年份增加,实际招生人数稳定在110人左右,而控制模型下的招生人数逐年增加。说明我院在提升导师软实力的条件下控制其招生规模,既能尽量满足国家社会发展的需要,也能间接保证硕士研究生的培养质量。
四、结论
1.通过对近三年录取考生的入学考试成绩分析可知:我院的生源复试线集中在310分左右。随着年份增加,考生总体成绩水平逐年提高,高分考生人数有所下降,需从招生工作初期采取积极措施尽量避免相对优秀生源的流失。
2.本文对考生复试总成绩与入学考试成绩、复试成绩的不确定关联进行了灰色关联度分析,计算可知:复试成绩是与复试总成绩发展趋势最接近的因素,突显了面试工作定量化在招生工作中的重要性,有利于我院做好研究生入学质量保证工作。
3.我院于2011年通过全国工程教育专业认证,作为入选24所高校中机械类专业唯一的“非985、211类”普通高校,在重大成套装备科研与教学方面具有传统优势和鲜明特色。在保证考试入学质量的同时,我院结合学科特色建立的招生计划分配模型可为中西部百所省属重点类院校的研究生招生工作提供参考。
[1]肖建琴.我国硕士研究生入学考试制度改革研究[D].武汉:中南民族大学,2012:1-17.
[2]余 刚,王晓芳.硕士研究生入学考试成绩回顾及定量分析[J].解放军医院管理杂志,2006,13(8):680 -681.
[3]曾文艺,张 颜,宋雯彦.研究生招生中模糊聚类分析方法[J].北京师范大学学报:自然科学版,2001,37(4):436-439.
[4]刘海燕,赵联文.研究生入学成绩对后续课程影响的统计研究[J].数学的实践与认识,1999,29(2):175 -178.
[5]黄建国.基于信息不对称理论的研究生招生问题探析[J].学位与研究生教育,2013(2):77-79.
[6]吴 萍,邹 彤,王櫵砚,等.中国研究型大学评估体系与研究生教育[J].中国高等医学教育,2006(6):16-19.
[7]曹明霞.灰色关联分析模型及其应用的研究[D].南京:南京航空航天大学,2007:7-18.
[8]Wu G D,Shang-Lien Lo.Effects of data normalization and inherent-factor on decision of optimal coagulant dosage in water treatment by artificial neural network[J].Expert Systems with Applications,2010,37(7):4974 -4983.
[9]Zhou C C,Hu D D.Research on inducement to accident/incident of civil aviation in southwest of china based on grey incidence analysis[J].Rrocedia Engineering,2012(45):942 -949.
[10]梁亦菡.研究生招生规模研究[D].上海:华东师范大学,2007:2-8.
[11]陈顺立.研究生招生规模建模与预测[J].计算机仿真,2012,29(2):396-399.
[12]骆轶姝,康 健,乐嘉锦,等.层次分析法在全日制硕士研究生招生计划分配中的应用[J].东华大学学报:自然科学版,2010,36(6):686 -690.
