基于ANSYS的负载轴端部受力分析

2014-04-27张冬梅马淑慧

科技视界 2014年24期

张冬梅马淑慧

（1.长江工程职业技术学院，湖北武汉 430212；2.北京工业大学，中国北京 100022）

0 引言

在现实生活及工程中，端部受力的旋转轴、杆件等结构比比皆是，例如起重机的起重杆、汽车车轮与其转轴、机床主轴[1]等，轴端受力而造成的轴变形需要控制在一定的范围内，以保证机器的精度及安全性。因此，本文采用有限元分析方法，借助ANSYS软件对某端部受力的负载轴进行有限元分析和相关力学计算，得到负载轴的变形和应力结果，并对该负载轴结构进行优化和改进，从而达到减小变形、提高安全性的目的。负载轴模型简化如图1所示。

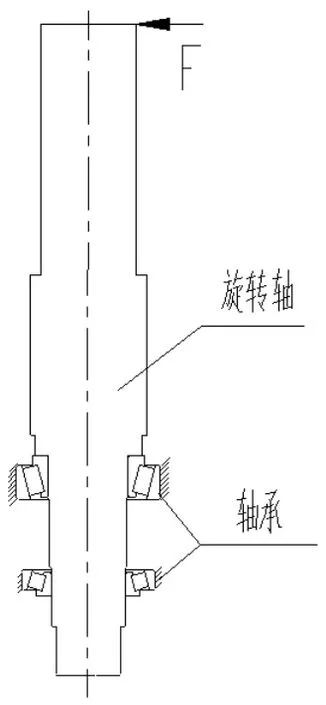
图1 负载轴示意图

1 理论分析和计算

1.1 轴承等效刚度的估算

上、下轴承均采用圆锥滚子轴承，利用圆锥滚子轴承刚度的简易计算公式[2-3]可以计算出轴承的径向刚度kr和轴向刚度kα，刚度计算公式如（1）、（2）所示

式中：

le——圆锥滚子轴承滚子有效接触长度（单位：mm），且le=l-2r；

l——滚子全长（单位：mm）；

r——滚子两端角；

Z——滚子数；

α——接触角；

Fα0——轴承预紧力。

对于有较高精度要求的机械，圆锥滚子轴承采用轴向预紧时的预紧力按（3）式确定

式中，d为轴承孔径（mm），括号中的系数，当转速高时取下限，反之取上限。该主轴的转速较低，因此，预紧力系数选择为40。

表1 轴承数据

将表1轴承数据代入到式（1）、（2）可计算得，上轴承的径向刚度和轴向刚度分别为6137.5N/μm和1953.3N/μm；下轴承的径向刚度和轴向刚度为3851.6N/μm和1193.8N/μm。

1.2 负载轴静力计算

对负载轴-轴承系统进行静力分析。负载轴通过轴承与支撑结构相连，轴承提供弹性支撑，建立负载轴受力及变形示意图，如图2所示，图中，F为轴端压紧力。计算时，压紧力取18KN。

轴端的最大变形Y，由负载轴本身的弯曲变形y1和轴承弹性变形而引起的负载轴前端变形y2叠加。y1和y2分别由公式（4），（5）求得。

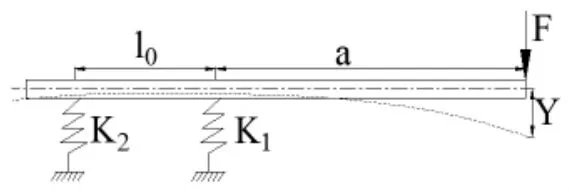
图2 负载轴变形示意图

式中：

EI——抗弯刚度；

k1，k2——上，下轴承的等效刚度。

对于负载轴，两轴承之间间距为190mm，上轴承与受力点之间的间距为 700mm，将数值代入（4）、（5）求得，y1为 0.65mm，y2为 0.13mm，由此可得轴端总变形量Y为：

Y=y1+y2=0.78mm

2 实体模型的建立和分析

2.1 模型建立

使用pro/E建立主轴的实体模型，并通过Pro/E与ANSYS的无缝接口，将模型导入ANSYS。由于轴阶梯较多，且存在小尺寸部位，因此，首先将轴进行分割，然后进行网格划分，并对要连接弹簧的面进行单元细分。建立分析模型时，将轴承简化弹簧组，使用ANSYS中的COMBIN14单元模拟轴承[4]。

2.2 模型计算结果分析

2.2.1 变形分析

使用ANSYS对负载轴-轴承系统进行静力分析，获得位移云图，如图3所示。由分析结果可得出，轴端最大变形为0.75mm，对于精度要求较高的机械而言，该变形明显偏大。

图3 主轴位移云图

2.2.2 应力分析

由应力云图4可知，最大应力出现在第四段轴末，即图中A点处。由于轴承简化为弹簧簇，因此在弹簧与轴连接处不可避免的会出现应力集中现象，因此，为了得到正确的负载轴应力，应观察轴承接触点的对称点的应力，由应力图可得，负载轴上等效应力最大约为60MPa。主轴材料为Q235-A，许用应力大约在113MPa（安全系数大）～147MPa，主轴危险截面最大应力接近材料许用应力的一半。

图4 负载轴应力云图

综上分析可得，该负载轴在工作状态下，将会产生较大的轴端变形，由于负载轴危险截面应力较大，将会降低主轴的使用寿命，严重时则导致安全事故的发生，因此需要对该负载轴的结构进行改进。

3 改进建议和方案

图5 加支撑后的位移云图

由于负载轴结构中两轴承间距较小，受力端远离轴承等原因，导致轴端变形过大，因此，可采用增加额外支撑点的方法改进轴的结构和受力情况。在上轴承与受力点之间，距上轴承与受力点之间距离的2/3处，增加额外支撑点并进行分析，得到位移云图和应力云图如图5、6所示。添加额外支撑点之后，轴端最大变形为0.05mm，即改进之后的轴结构最大变形减小了93%，最大应力减小了83%，负载轴变形情况有了非常大的改观，同时应力也得到了相应的改善。