非平衡与多相复杂系统模拟研究—Lattice Bo ltzm ann动理学理论与应用
2014-04-26许爱国张广财李英骏李华
许爱国*,张广财,李英骏,李华
1.北京应用物理与计算数学研究所计算物理重点实验室,北京100088 2.北京大学应用物理与技术研究中心和高能量密度物理数值模拟教育部重点实验室,北京100871 3.理论物理国家重点实验室(中国科学院理论物理研究所),北京100190 4.中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室,北京100083
非平衡与多相复杂系统模拟研究—Lattice Bo ltzm ann动理学理论与应用
许爱国1,2,3*,张广财1,3,李英骏4,李华1,2
1.北京应用物理与计算数学研究所计算物理重点实验室,北京100088 2.北京大学应用物理与技术研究中心和高能量密度物理数值模拟教育部重点实验室,北京100871 3.理论物理国家重点实验室(中国科学院理论物理研究所),北京100190 4.中国矿业大学(北京)深部岩土力学与地下工程国家重点实验室,北京100083
在自然界和工程物理领域存在大量的非平衡、多相等复杂系统和复杂行为。Lattice Boltzmann(LB)方法起源于复杂系统复杂行为研究的格子气或元胞自动机模型;其中,现代版的Lattice Boltzmann Kinetic Model(LBKM)植根于非平衡统计物理学的基本方程—Boltzmann方程。本文从物理学视角评述LB方法,给出单松弛因子和多松弛因子LBKM构建的统一理论,介绍其在非平衡与多相复杂系统研究方面的应用。简单列举LB在多相流、可压流、材料动理学等方面的进展,重点介绍使用LB研究流体界面不稳定性、燃烧等问题的工作。本文所重点传递的信息为:可以通过宏观量研究系统的非平衡行为、可以提供系统偏离热力学平衡引发的宏观效应是LBKM建模优越于宏观连续介质建模的地方;除了可以从更基本的层面理解相应物理系统的特征、机制和规律外,这类研究结果可以为现有程序或软件中宏观模型的改进(例如修正项的构造)提供物理参考。
格子玻尔兹曼;动理学模型;非平衡效应;复杂系统
目录
I.引言 136
II.LB方法的诞生与发展概述 137
III.LB理论与应用 138
A.整体评述 138
B.研究现状与曾经的困惑 142
C.LB动理学模型 142
1.LBGK动理学模型 143
2.MRT-LB动理学模型 147
D.LB动理学模型与非平衡效应 149
IV.LB应用实例 150
A.燃烧问题的LB建模与模拟 150
1.早期研究 150
2.我们的模型 150
3.爆轰过程中的非平衡效应初探 151
4.小结 153
B.流体不稳定性的LB建模与模拟 154
1.RM不稳定性研究 154
2.KH不稳定性研究 157
3.RT不稳定性研究 160
V.总结与展望 162
致谢 162
163
I.引言
除了日常生活中常见的各类复杂流动过程外,工业领域存在大量的种类各异、起源不同的非平衡与多相复杂流体系统。首先,强冲击与爆轰产生的压强可以达到数十万个大气压,是多数固体材料屈服应力的几十倍。当如此强的冲击波在固体材料(包括炸药)内进行传播时,波后物质表现出流体行为,相当一部分动力学、动理学特征可采用流体模型来描述。由于实际材料内往往存在着大量的孔隙、杂质、颗粒等局部微介观结构,冲击波作用过的区域属于典型的复杂、多相、可压流体系统。这一系统的演化涉及到高应变率、多尺度和动态物理场,动力学非平衡和热力学非平衡效应显著,其物理建模、模拟和分析均具有较强的挑战性。燃烧、爆炸等化学反应过程的介入使得系统的复杂程度进一步剧增[1]。
其次,在新能源领域,核聚变能在利用过程中不会产生二氧化碳等有害物质,不存在原料问题,不存在发生裂变的危险,是一种安全、清洁、原料蕴藏丰富、对环境污染少、能最大程度为人类所利用的优质能源。有效利用核聚变能的前提是实现可控的核聚变反应。为了实现这一理想,世界各国的科学家们已奋斗了大约半个世纪,提出了多种可控核聚变模式。其中,ICF(Inertial Con fi ned Fusion,惯性约束聚变)的关注度最高[2]。ICF内爆过程同时涉及多种非平衡与多相等复杂动力学行为。其中最典型的就是三种流体界面不稳定性及其引发的混合行为。ICF的驱动源可以是高强度的激光,也可以利用高强度的粒子束,以脉冲的形式向外输出能量,作用对象是充满氘氚燃料的球状靶丸。其基本物理图像如下:激光或粒子束均匀照射靶丸外表面,外表面的物质由固体转变为等离子体;由此产生的高压和动量守恒会对内部的氘氚燃料产生高强度冲击压缩以达到聚变反应条件。在反应和放能过程中燃料自身的惯性起到了约束燃料飞散的作用。ICF所用的靶丸通常是由多层介质组成,在内爆过程中产生的各种冲击波和稀疏波使靶丸内部介质的各个界面的扰动相互耦合。烧蚀冲击波在通过靶丸每层界面的时候都会引起RM(Richtmyer-Meshkov,瑞奇迈尔–莫西科夫)不稳定性的增长,而RM不稳定性的发展又会带来其它不稳定性的增长:在内爆加速阶段,轻材料包层加速重材料(金属)会引发RT(Rayleigh-Taylor,瑞利–泰勒)不稳定性;在反弹阶段,气芯的轻材料加速重材料壳层,同样引发RT不稳定性。在RT不稳定性发展的后期,轻重流体两侧的大变形切向流又会导致KH(Kelvin-Helmholtz,开尔文–亥姆霍兹)不稳定性的增长,出现卷曲、翻滚的现象,局部界面加速(轻介质推重介质时)同样又会进一步引发小波长的RT不稳定性,伴随产生的许多短波长扰动会加剧界面两侧附近等离子体的混合。流体不稳定性的存在与发展,极大地影响ICF的内爆过程。在核武器内爆过程中存在类似的物理图像和流体界面不稳定性等复杂问题[3]。因此,流体不稳定性研究是ICF点火研究、核武器物理研究中的关键问题。
鉴于相分离、混合、多相流动、流体界面不稳定性、燃烧等复杂动力学问题在许多工业过程、自然现象和武器物理当中的普遍性,其研究具有重要的基础与现实意义。由于这些复杂流体系统的非线性发展往往涉及强非线性和多尺度,在燃烧和流体界面不稳定性等演化过程中甚至会涉及到湍流等老大难问题,所以其理论研究进展缓慢;在实验研究方面,三维流体系统中的各种复杂特征和结构对诊断技术要求较高。所以,数值模拟是这些复杂流体系统研究的重要手段。
上述复杂系统在演化过程中存在大量的动力学与热力学非平衡过程和效应。而传统数值模拟依赖的是Euler方程、Navier-Stokes方程等宏观连续动力学模型,这些模型是基于平衡态或近平衡态近似的。与平衡态动力学模型Euler方程相比,Navier-Stokes方程中包含了黏性和热传导效应。根据气体动理学理论,热传导和黏性的出现本身就是系统偏离热力学平衡的表现和效应。但流体系统偏离热力学平衡的效应非常丰富、非常复杂,仅仅靠在动力学方程中引入热传导项和黏性项来描述是远远不够的。LB(Lattice Boltzmann,格子玻尔兹曼)方法基于非平衡统计物理的基本方程Boltzmann方程。可以通过宏观量研究系统的非平衡行为、提供系统偏离热力学平衡引发的宏观效应是LB动理学建模优越于传统宏观流体力学建模的地方[4,5]。
II.LB方法的诞生与发展概述
LB方法或模型是近三十年以来迅速发展起来的一种全新的复杂系统建模方式和模拟工具[6~8]。由于它基于非平衡统计物理的基本方程Boltzmann方程,所以对于系统中那些局域的、动态的、偏离热力学平衡不同程度的复杂动力学、动理学行为具有物理描述上的自适应性。目前,LB理论和应用研究已渗透到诸多学科和研究领域,成为国际热点研究课题之一[5,9~17]。
LB方法的前身为“格子气”或“元胞自动机(CA, Cellular Automata)”模型。格子气模型的早期研究可以追溯到上世纪六十年代。其基本思路如下:真实流体是由大量粒子组成的。但是流体力学微分方程的形式并不依赖于微观过程的细节,而仅仅决定于微观守恒律和对称性(只有一些输运系数如粘滞性依赖于微观的细致情况)。基于这一设想,人们开始使用较简单的离散模型来作为连续流体系统的理想化模型。为能模拟连续流体系统,特别是为了让在微观层次上破缺的对称性在宏观上得到恢复,元胞自动机的结构需满足一定的条件—对称性约束。与现代LB研究直接相关的格子气模型出现于1986年,Frisch,Hasslacher和Pomeau给出了一个后来以他们名字命名的六角模型[18]。这个模型只在动量空间中选取六个离散的点,就在连续极限下恢复了流体动力学方程。它的出现使人们认识到,系统的许多宏观动力学行为只取决于局域的对称性和守恒律,而对具体分子的运动细节不敏感。这种介观模拟手段随后快速发展为基于统计物理并与热力学自恰的LB方法。
到目前为止,在二十多年的时间里,欧美日等发达国家的科学家已经在这一新兴领域进行了较密集型的研究。通过google学术搜索关键词“Lattice Boltzmann”可获得约282,000条结果1搜索时间为2013年11月19日下午16:00。仅美国物理学会的Phys.Rev.和Phys.Rev.Lett.系列就已发表相关研究论文数百篇2LB涉猎的范围是如此之广,参考文献是如此之多!本文重在突出研究思路,列出的参考文献仅仅是例子。;其中,发表在Phys.Rev.Lett.的研究论文有50余篇。在LB发展过程中,一些工作于国内外的华人科学家也做出了重要的贡献[5,7,8,19~52]。粗略地说,文献中的LB模型可以分为两个大类:其中一类工作是将LB模型作为恢复或求解Navier-Stokes等偏微分方程的一种全新的思路和方法;另外一类工作是将LB模型与传统流体力学模型并列,将其视为一种全新的、微介观动理学模型。在目前已有的文献中,第一种类型的LB模型研究占了绝大多数;在这些研究中,LB在算法方面的性质和特点是主要研究内容。在第二种类型的LB模型研究中,基于连续介质建模的传统流体模型所不能描述(或描述不好)的高Kn(Knudsen,努森)数效应、非平衡效应是关注的重点3物理系统的动力学模型通常用偏微分方程表示。在本文中,LB动理学模型与作为解法器或替代品的LB模型的区别为:前者包含相应的连续模型所没有包含的更底层信息,可以用于研究传统模型所不能描述的一些现象和行为;而后者在描述的物理行为上等同于对应的宏观连续模型。。从应用角度来说,除了常见的复杂流体之外,LB方法已被推广应用于连续介质建模失效的高Kn数流体系统[53~55];已被推广应用于晶体生长动力学[56~59]、半导体动力学[60]、固体力学[61~64]、声子动力学[65]、金属泡沫生长动力学[66]、裂纹生成与发展动力学[61]、玻色–爱因斯坦凝聚[67]等领域;LB思想已被移植应用于量子力学[6,68,69]、相对论[15,70]、电动力学[71]、量子场论[72],为学科建设提供了新的思路;LB技术已启发产生了正在兴起的LFP(Lattice Fokker-Planck)技术[73~75]。如果将LB视为求解偏微分方程的新思路[52,76~88],那么LB适用的范围几乎含盖了我们所关心的绝大多数物理系统(因为几乎所有物理系统的演化都遵循偏微分方程)。LB方法的快速发展已经催生了新的商业软件PowerFlow[89]和开源软件OpenLB[90]、Palabos[91]等。
III.LB理论与应用
A.整体评述
美国国家基金会理事会成员、总统科学顾问、工程院院士、文理学院院士、中国科学院院士、已故著名学者田长霖曾有过如下评述:“尽管许多物理现象和工程问题是在宏观或‘人’的尺度上体现出来的,但其根源仍然始于分子尺度。建立跨越多个时空尺度的物理模型有一定困难,lattice Boltzmann方法可望能够为此提供有效的手段”[92]。LB方法具有如下属性:(1)LB基于非平衡统计物理学的基本方程(Boltzmann方程),对于复杂流体系统中的一些多尺度(不同Knudsen数)行为具有物理描述上的自适应性,因而经常被称为“多尺度方法”;(2)一个好的离散速度模型可以看做是对分子运动细节做了某种平均化处理,因而LB比分子动力学方法要粗糙,但与宏观Navier-Stokes模型相比又含有更多的微介观动理学信息,经常被称为“介观方法”;(3)从离散的网格来说,LB具有Euler方法的属性;从离散的粒子观点来说,标准LB方法又具有Langrange方法的属性。因而,是一种“混合方法”;(4)该方法实现了用本来就不连续的模型去描述连续的客观对象并进行直接计算的设想。
尽管LB起源于物理(复杂系统研究的格子气或元胞自动机模型),但随着对算法细节要求的逐步提高,越来越多的计算数学家介入,越来越多的对算法不太熟悉同时又有其他关心问题的物理学家逐渐转移了兴趣。在LB领域,目前的现状是数学家远多于物理学家,因而将LB作为偏微分方程的一种全新的模拟方法的研究、结构与非结构网格研究、离散格式研究、精度与误差等的研究占了绝大多数。从物理学角度来看,LB基于非平衡统计物理学的基本方程Boltzmann方程,可以视为Boltzmann方程的一个特殊的离散化。因此,合理的LB动理学建模应该能够有效地继承Boltzmann方程描述的部分功能。例如,其适用的物理范围应该比传统计算流体力学(CFD, Computational Fluid Dynam ics)更宽广;应该可以用于研究与我们关心的动力学行为关系最密切的一部分非平衡特征及其演化规律;或许,可以借助于LB动理学模型发展出一套新的非平衡行为描述方法或测量手段。
LB从其前身格子气、元胞自动机模型开始,就受到了我国一大批科学家(例如,北京应用物理与计算数学研究所的陈式刚院士[19,93]、沈隆均研究员[52]、复旦大学的陶瑞宝院士[94]、北京师范大学的黄祖洽院士[95]、中科院过程工程研究所的李静海院士[96]、西安交通大学的陶文铨院士[8]、北京大学的赵凯华教授[97]等)的高度关注。在LB国际会议或文献中出现频率较高的华人学者名单正在迅速延长。
LB起源于物理,服务于物理。物理应用是目的和归宿。下面我们简单列举LB在几类复杂系统研究方面的进展。
多相复杂流体系统方面:多相复杂流体系统一直是LB研究的重要领域。多相流LB模型构造的核心是如何将非理想气体效应合理地加入演化方程。虽然模型的具体形式各异,但其最终目的都是将理想气体状态方程更换为合适的非理想气体状态方程,其中的周期性等特征尺度通过界面项来描述或控制。由于LB模型的早期研究主要集中在等温、低速、不可压流体系统,所以早期的多相流模型也主要集中在等温、低速、不可压流体系统,主要有着色模型、伪势模型、自由能模型和Enskog型外力模型。着色模型最初由Gunstensen等[98~100]提出。这是源于Rothman和Keller[101]的一个二元格子气模型。在该模型中,使用红色和蓝色粒子来代替两种不同的流体。两相间的分离和混合通过控制基于颜色梯度的粒子间相互作用力来实现。伪势模型最初由Shan和Chen[27]提出。该模型通过引入粒子间非局域相互作用势即伪势来模拟两相流系统。相互作用的形式决定了状态方程的形式,只要其选取合理,两相间的分离与混合就可以合理地实现。除表面能外,相互作用势(或力)描述、状态方程描述和自由能表述是等价的。自由能模型最初由牛津大学Yeomans课题组的Sw ift等[102,103]提出。在自由能模型中,系统的基态由自由能极小值来决定。在高温条件下,系统自由能只有一个极小值,系统处于均匀混合态。当系统温度降低至二相共存温度时,自由能的形式转变为具有两个相等的极小值,这时原来的均匀混合态失稳,从而发生相分离现象。1997年,同一课题组的Gonnella等[104]在Sw ift等模型的基础上引入序参数的二阶空间导数平方项,构造了层状相生成和演化的自由能LB模型。Gonnella课题组的许爱国等修正了原Sw ift等模型中压强和迁移率等矩关系的定义式和平衡态分布函数计算公式[34],提出通过负反馈等机制来提高LB模拟过程中的数值稳定性[36],在原层状相生长LB模型的基础上给出了修正的压强和迁移率定义式以及平衡态分布函数计算公式,通过模拟研究给出了层状相演化过程中的一个普适的标度关系[35]。1999年,陈十一课题组的He等[105]提出了Enskog型外力模型,并且在Rayleigh-Taylor不稳定性的LB模拟方面做了些探索。物理应用是LB方法存在和发展的灵魂。只有在具体应用过程中,LB方法或模型研究才能真正做到查缺补漏,逐步走向成熟。Yeomans课题组、Gonnella课题组、许爱国课题组等在注重模型构建的同时,在模型的实际应用方面进行了大量的探索,在相分离和层状相生长演化方面获得了一系列新的认识和规律[34~38,40,41,102~104,106,108]。
上述模型都是等温模型。一般来讲,等温模型是假设系统与一个无限大的热浴充分接触,相变过程中适时地从热浴吸收或向热浴释放热量以维持系统温度恒定。等温模型适用于整个演化过程中系统内的温度基本均匀且基本恒定的情形,例如相变潜热较小的情形。但在很多情形下,温度场效应是重要的,甚至是起关键作用的。因此,建立适用于热多相流的LB模型是一项重要的基础性工作。近年来,Gonnella课题组实现了含温度场效应的单介质多相流的LB建模与模拟,获得了一些新的规律性认识[108]。其建模的主要思路为:通过加外力项实现状态方程的调换。我们课题组的甘延标等人进一步发展了上述思路,并在具体计算技术方面提出了使用快速傅里叶变换(FFT, Fast Fourier Transformation)来计算空间导数的方案,使得实际模拟过程中总能量得以更好地保持守恒,从而获得了FFT-TLB(FFT-Thermal Lattice Boltzmann)模型[40];借助于形态分析技术[109~113],给出了液气相变动理学过程中一系列深刻认识[40,41]。文献[40]对比研究了等温与温度自适应模型在液气相分离动理学方面表现出的差异。发现,等温模型给出的新相区域增长速度偏大,图1和图2给出一组等温相分离与温度自适应相分离模拟结果的对比。在图2中,结构因子的另一种含义为等时相关函数;结构因子极大值处波数的倒数给出系统的一个特征尺度;结构因子极大值点随着时间向波数减小的方向移动说明:新相区域的特征尺度随着时间逐渐长大。图3给出密度、温度梯度场随时间演化的例子。通过它可以更好地理解新相区长大的具体动理学细节(例如长大速率等)。具体参数参见原始文献4这一工作被选入PRE Kaleidoscope做永久展示。文献[41]首先基于形态分析技术给出了液气相分离SD(Spinodal Decomposition,扭结分离)和DG(Domain Grow th,相区增长)两个阶段分界点的严格判据:在SD阶段,界面面积在不断增大,而进入DG阶段后界面面积逐渐减小,故界面面积最大点即为SD和DG两个阶段的分界点。在图4中边界长度L(t)曲线的极大值点对应SD和DG两个阶段的分界点。本工作进一步细致研究了热传导、黏性和Prandtl数对相分离动理学的影响。图4给出的是不同Prandtl数或热传导系数对相分离过程的影响5这一工作被收录EPL Highlights of 2012。
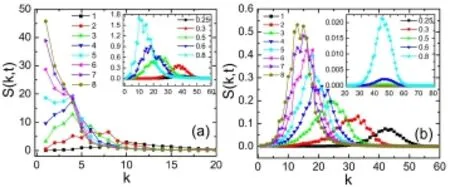
图2. 相分离过程中的结构因子。图(a)是等温情形,图(b)是温度自适应情形
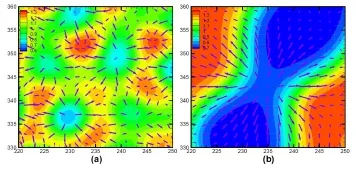
图3. 非等温情形下的密度和温度梯度场。其中图(a)对应t=0.8,图(b)对应t=7.0
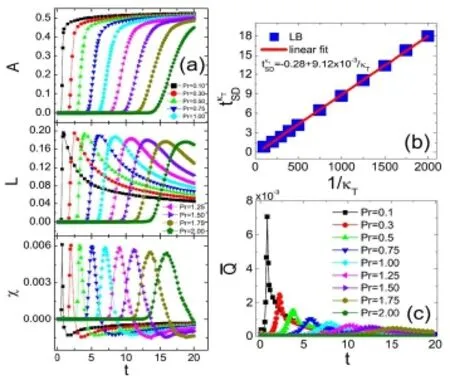
图4. (a)热相分离过程的形态学描述;(b)相分离SD阶段持续时间和热传导系数之间的关系;(c)不同热传导系数下系统平均热通量的演化曲线
高速可压流体方面:由于冲击、爆轰等问题在工程和科学领域的重要性,高速可压流体的LB建模与模拟研究从一开始就受到了广泛关注。因为Mach数大于1是系统存在稳定冲击波的前提;爆轰波可以看作是由(化学反应)能量补充的冲击波。根据物理图像和对应离散格式的不同,开展这方面研究所采用的理论框架也有所不同。最早的尝试是在标准格子气模型、LB理论框架下进行的。1988年中国工程物理研究院的陈式刚、聂小波就针对可压流体模拟提出了一个格子气模型[19]。1992年,Alexander等[114]提出一个可压流体LB模型,其关键技术是引入一个可调的声速,通过减小声速来提高Mach数。这个模型针对的还是近似等温的可压流体系统。1999年,闫广武等[115]提出一个可用于求解、模拟Euler方程系统的LB方法。在这个方法中使用了一个三能级离散速度模型。后来,孙成海等[116~119]发展了一个粒子速度随Mach数和内能改变的LB模型,在一定程度上突破了粒子速度为常数的限制。2006年,单肖文等[120]给出一个较系统的理论框架:通过Maxwellian分布的Hermite张量展开来离散Boltzmann方程。在2007年舒昌课题组提出的模型[121]中,使用了一个满足恢复Navier-Stokes方程所需统计关系的圆函数来取代传统的Maxwellian分布函数。2008年聂小波等使用高阶矩关系在标准LB框架下构造了一个高速可压模型[122]。近年来,冉政课题组基于冲击波界面的捕捉技术、Lie对称守恒和熵等思想在可压流体系统的LB方法方面取得了一系列进展[123~126]。
另外一条有效途径是有限差分LB(FDLB,Finite-Di ff erence LB)方法。近年来,日本神户大学的Tsutahara课题组[127~129]提出并发展了一套很有启发性的建模思路。许爱国[37]将这一思路推广应用至二元流体系统。FDLB摆脱了空间离散化和时间离散化之间的绑定,使得粒子速度可以灵活选取。同以前的LB模型类似,这些模型只能稳定模拟低Mach数流体系统。LB的数值稳定性问题已经被许多学者关注了数年,改进的主要途径主要包括:熵方法[130~133]、FIX-UP方法[134]、通量限制技术[135]、多松弛因子模型[31,45,136,137]等。
我们课题组的观点是[5]:影响LB模型数值稳定性的原因可划分为两个方面:(i)物理模型构建方面的原因;(ii)数值离散格式方面的原因。这两个方面的因素耦合在一起作用。从物理建模角度,早期的绝大多数LB模型研究主要集中在单松弛因子模型即BGK模型方面。在原始的BGK模型中,所有动理学模式趋于热力学平衡的速率都用一个常系数来描述,它不随系统中密度、压强等因素的改变而改变。这相当于对所有动理学模式的快慢做了个平均化处理。自然地,它可以很好地描述所有动理学模式趋于平衡速率相差不大的系统。但实际上,在界面附近(特别是在冲击波、爆轰波附近),密度、压强等的梯度比远离界面区域要大得多。这些较大的密度、压强梯度等会驱动系统更多地偏离热力学平衡,所以界面附近的黏性和热传导效应实际上比单相内部要显著得多。所以,我们课题组在高速可压流体LB研究方面的第一个工作就是在LB方程中引入合理的补充黏性项[138]。由于当时在模拟过程中将时间步长与系统的Knudsen数在数值上做了等效处理(这是在LB方法中使用较普遍的一种处理方法),所以这个LB模型实际上是高速可压Euler方程的一个新的数值解法或模拟方法。第二个工作是在不使用上述等效处理的情形下,发展了一个高速可压流体系统的LBGK模型[139]。在连续极限下,这个模型可以恢复Navier-Stokes方程。这个模型是适用于高速可压流体系统的第一个LB动理学模型。随后,我们在减少离散速度数目、提高运算效率[140]和三维高速可压流体LB建模方面[141]做了些工作;在进一步的工作[142,143]中,引入了合理的通量限制器,在单松弛因子模型框架内实现了Prandtl数可调,使得高速可压流体系统LBGK模型的发展更加成熟[5]。
我们课题组“通过物理建模改进来提高LB模拟稳定性”的第二方面工作就是构建多松弛因子LB模型。第一个工作[44]是基于群表示理论来构建转置矩阵和矩空间中的平衡态分布函数。第二个工作[45]是基于Maxwellian分布函数需要满足的矩关系构造转置矩阵和矩空间的平衡态分布函数。第一个工作的目的是构造高速可压Navier-Stokes方程的LB数值解法或模拟方法,所以构造过程灵活性较高。第二个模型的构造与Maxwellian分布的矩关系一致,所以可以用于研究系统的非平衡特征,是一个LB动理学模型。最近,我们课题组“通过引入分裂算符”和“通过矩关系反求离散速度空间的平衡态分布函数”,在不使用额外黏性项的条件下实现了高速可压流体的LBGK建模[43,144]。由于标准LB模型对离散速度大小的限制严格,而FDLB中离散速度模型的构造和空间、时间的离散化相对独立,所以FDLB模型在高速可压流体建模与模拟方面取得了长足的进展。
材料动理学方面:固体力学LB的前身—CA模型在固体材料动力学的模拟方面最近有一个较显著的进展和突破。CA模型已经在各类复杂流体系统的研究获得了广泛的应用。固体材料动力学行为的CA建模与模拟也很早就引起人们的兴趣[61]。但由于固体材料特有的屈服强度、剪切、硬化、断裂、与变形历史相关等性质,传统CA建模思想的直接延伸和使用受到了很大的限制。所以固体材料动力学的CA建模研究进展缓慢。日内瓦大学的Chapard课题组通过使用两套网格建立了可以恢复波动方程的固体材料CA模型,这在当时是个重要的突破。但是,Chapard等人的模型是准一维的。在该模型中,两个不同方向上的运动不能相互耦合,因此不能描述固体材料的泊松比。我们课题组的董银峰等[64]在该模型的基础上,通过修正碰撞、传递等规则使得泊松比效应得到合理描述。其中的关键技术在于八个系数矩阵的构造,这是本工作的主要贡献。需要强调的是,CA模型与有限元等其它模拟方法关注的物理内容并不完全相同。其主要用途不是与具体的实验数据作比对,而是通过构建规则恢复宏观行为来理解宏观现象背后可能的物理机制。
方海平课题组及其合作者在LBGK模型的理论完善[146,147]、血液和粒子悬浮流体系[148~153]、微流动系统[154]的LB模拟等取得了一系列进展;2003年他们针对光子带隙材料中电磁散射问题提出一个LB模型,这个模型不仅适用于周期系统,同样也适用于含缺陷和无序的情形[155]。郑志刚[156]、康秀英[157~161]、徐远清[162~167]等课题组也在血液流、细胞形态与操控以及生物游动等的LB模拟方面进行了研究。王沫然课题组在流固耦合、微管道流等的LB算法方面进行了一些探索[168~172]。孙其诚课题组将多松弛因子LB模型与离散元方法相结合,模拟研究Bingham塑性流问题[173]。程永光课题组将LB方法应用于水电站高维流场等的模拟研究[174,175]。
此外,LB方法在多孔介质流[174,176~187]、粒子悬浮体系[188~192]、非牛顿流体[193~196]、磁流体[20,197]等领域都有着广泛的研究。限于篇幅和与本文主要内容的关联度,这些工作的具体思路与细节请参阅相关文献。
B.研究现状与曾经的困惑
尽管LB起源于物理(复杂系统研究的格子气或元胞自动机模型),但随着对算法细节要求的逐步提高,越来越多的计算数学家介入,越来越多的对算法不太熟悉同时又有其他关心问题的物理学家逐渐转移了兴趣。在LB领域,目前的现状是数学家远多于物理学家。因而将LB作为偏微分方程的一种全新的模拟方法的研究、结构与非结构网格研究、离散格式研究、数值精度与误差等的研究占了绝大多数。这些方面的工作固然重要,但从物理学角度来看,LB基于非平衡统计物理学的基本方程Boltzmann方程,其作为一种全新的动理学(Kinetic)模型在物理描述方面的优势远没有获得充分挖掘,这方面的理论研究与应用研究还较少。
以前的绝大多数LB模拟都是在做传统方法能做的工作。所以,曾一度有人怀疑LB只能做传统方法能做的事。选用LB与否,取决于算法方面有无优势和使用者的方便程度。后来,部分研究者将目光转移到了Knudsen数较高的情形(例如,边界层流、微管道流等)。这里,连续模型不存在。LB在高Knudsen数系统的研究现在已有了一些探索。下面留下的困惑是:在传统连续模型(例如Navier-Stokes)存在的情形下,LB有无优势?这是个等待回答的理论问题!同时,高Knudsen数往往意味着系统尺度较小。而我们关心的系统恰恰是整体上Navier-Stokes等传统连续模型成立,而其中又存在大量的微介观结构,这些微介观结构在挑战着物理描述的合理程度。
在复杂流体系统中,存在大量的动力学与热力学非平衡问题。动力学非平衡(例如压强、密度、流速、温度的空间梯度)触发热力学非平衡。热力学非平衡行为与效应是与各种界面(物质界面、力学界面)相伴随的。在存在大量界面的复杂系统中,非平衡行为及效应非常丰富与复杂。传统连续流体动力学模型(例如Navier-Stokes方程)显然无法描述和研究如此丰富的非平衡行为和效应。在2012年的综述文章[5]中,我们指出:可以通过宏观量研究系统的非平衡行为、提供系统偏离热力学平衡引发的宏观效应是LB动理学建模优越于传统宏观流体力学建模的地方。随后,这一思想在燃烧与爆轰模拟、RM不稳定性研究、冲击波的规则与Mach反射等领域得到了初步的应用[39,40,45]。
C.LB动理学模型
构建LB动理学模型,首先要回到Boltzmann方程和流体力学方程的关系:流体力学方程可以由Boltzmann方程通过Chapman-Enskog多尺度展开技术来获得[198]。如果我们将分布函数f(x,v,t)视为Knudsen数Kn的函数f(x,v,Kn,t),那么Kn=0对应系统的热力学平衡态。其中的Knudsen数为分子间距与我们关心的特征尺度之比。热力学平衡态分布函数记为f(0)或feq。我们将分布函数f、时间导数和空间导数在Kn=0附近做如下泰勒展开:

我们会发现:当系统处于平衡态(f=f(0))时,流体系统的动力学方程为Euler方程;当需要考虑一阶偏离(f=f(0)+Kn·f(1))时,流体系统的动力学演化方程为Navier-Stokes方程;当需要考虑二阶偏离时,流体系统的动力学演化方程为Burnett方程;当需要考虑二阶以上偏离时,流体系统的动力学演化方程统称为超Burnett方程。根据Knudsen数(Kn,Kn=l/L,l为分子平均自由程或平均分子间距,L为我们关心的特征尺度)可以将流体划分为以下几类:Kn≤0.001的系统称为连续流;0.001<Kn≤0.1的系统称为滑移流;0.1<Kn≤10的系统称为过渡流;Kn>10的系统称为自由分子流。从物理描述上来看,从连续到离散是逐渐过渡的。在分子平均间距基本为常数的前提下,关心的特征尺度越大,系统就表现得越连续;反之,关心的特征尺度越小,离散效应就越显著。这很类似拿着放大镜观测某种材料:平均分子间距l基本为常数,通过放大镜能看到的视野尺度就相当于我们关心的特征尺度L。放大镜的倍数越高,我们看到的视野L就越小。当放大镜的倍数不大时,我们看到的材料是连续的。当放大镜的倍数增加到一定程度,我们看到的视野L减小到一定程度,就会看到分子或原子的离散分布。根据经验,当Kn>0.001时连续介质建模就开始受到挑战。
1.LBGK动理学模型
a.基本理论
如果碰撞项采用Bhatnagar-Gross-Krook(BGK)[199]模型,则Boltzmann方程可写为:
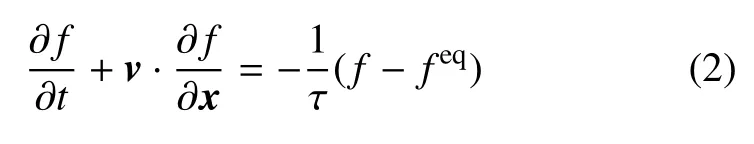
其中τ为松弛时间因子,粒子速度v为连续变量,feq为Maxwellian分布:
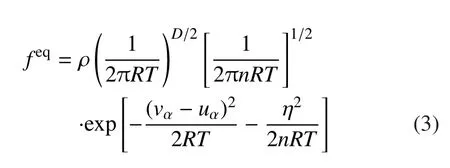
其中,D表示空间维数;n为额外自由度的数目,与比热比γ的关系为
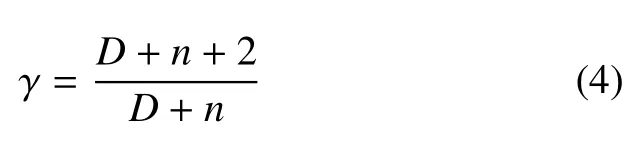
将粒子速度v作特殊离散化之后的Boltzmann BGK方程为:
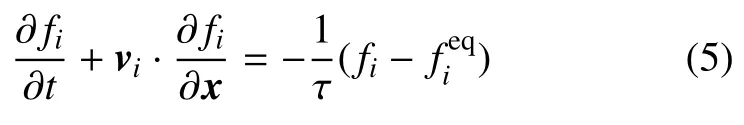
其中fi=f(vi)。基于上式构建的LB模型通常称为LBGK模型。通过上式进行模拟最关键的一步就是的计算。我们的思路如下:由(2)式到(5)式,将粒子速度空间或分布函数离散化之后,必然会丢信息;但只要处理得当,部分信息仍会保留下来。我们根据具体研究需求确定哪些信息是必须保留下来的。
我们知道,Maxwellian分布feq满足一个无穷长的矩关系系列;离散化的不可能满足feq的所有矩关系。那么问题就聚焦在:哪些矩关系是必须保证满足的?要回答这个问题,我们对(2)式和(5)式同时做Chapman-Enskog多尺度分析。其中唯一的区别就在于:在(2)中矩关系是以积分形式出现的,而在(5)式中矩关系是以求和形式出现的。我们要求积分形式的矩关系与求和形式的矩关系严格相等。这样,就可以保证(2)式和(5)式在连续极限下对应同样的宏观流体力学方程。很显然,“哪些矩关系是必须满足的”取决于我们的研究需求,即取决于我们希望所设计的模型在连续极限下对应的宏观流体力学方程。首先假设我们的目的是让离散化之后的Boltzmann方程(5)与原始连续的Boltzmann方程(2)在Kn≤0.001情形下对应完全相同的Navier-Stokes方程:

Maxwellian分布函数积分形式的矩关系有解析结果,见上述7个矩关系中间部分;ηi对应分子平动以外的自由度。上述7个矩关系可以统一写为


可见,离散速度模型(Discrete Velocity Model,DVM)的选取灵活度是很高的。到这里,基于BGK模型(即单松弛时间因子模型)的LB动理学模型物理建模完成。
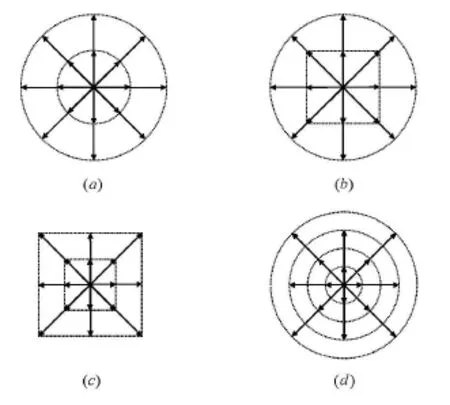
图5. 几种离散速度模型的示意图
当然,在C-1存在的情形中,离散速度模型的具体形式(包括能级和离散速度方向、大小的选取)对于LB模拟的数值稳定性可能有影响。我们的研究经验给出如下迹象:时数值稳定性要好。为了提高数值稳定性,同时也为了方便进一步挖掘LB作为一个非平衡复杂系统动理学模型在物理描述方面的优势,我们建议:尽量采的数值跟Maxwellian分布接近用能够使得的数值跟相应Maxwellian分布接近的离散速度模型。需要指出的是,上述建模思路独立于系统的Mach数,因而所构建的LBGK模型既适用于低速近似不可压流体系统,又适用于高速可压流体系统。同时,基于这种思路构建的LB模型所需离散速度数目最少。例如,二维LB模型只需16个离散速度。图5给出几种二维DVM的示意图。图(a)~(d)中的DVM可以分别表示为:
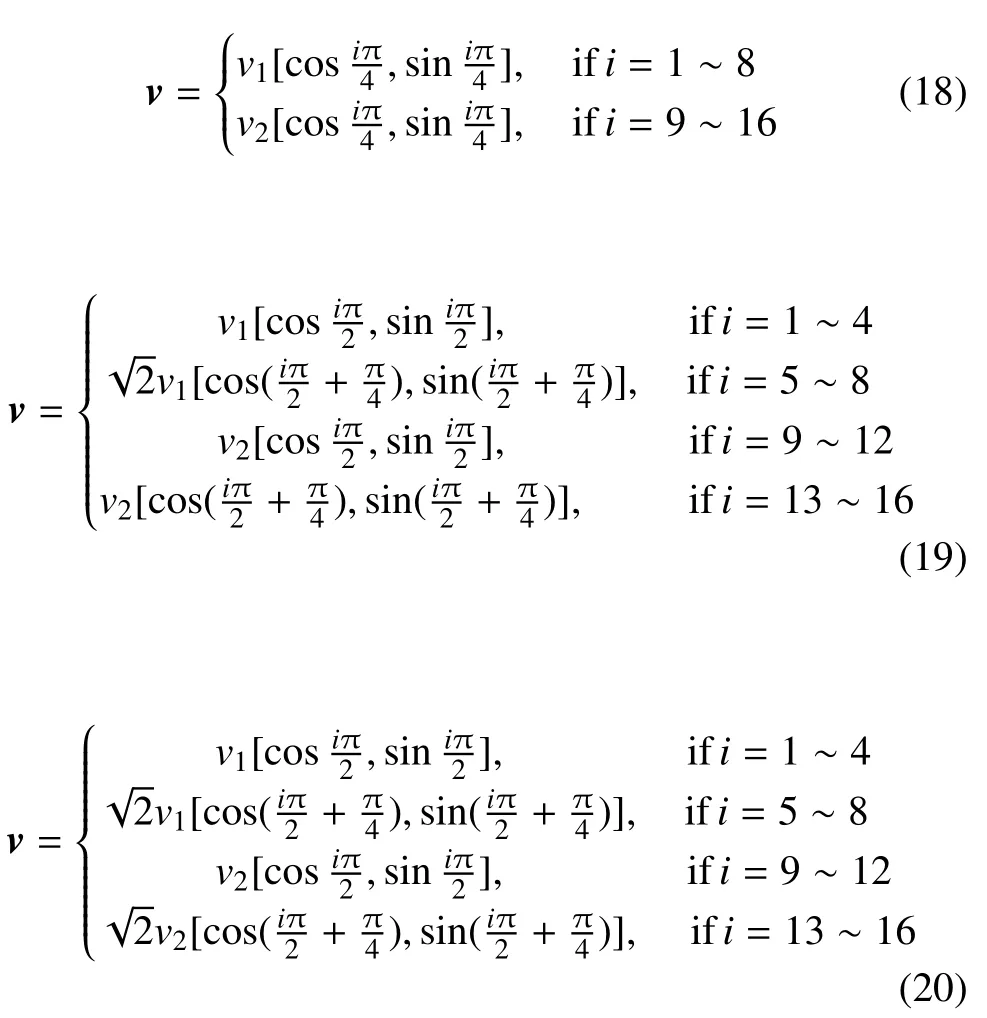

其中,vi(i=1,2,3,4)为离散速度大小。在二维情形:
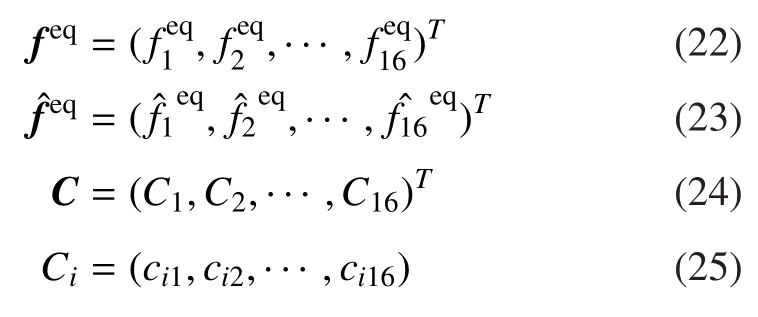
其中,上标T表示矩阵转置。同理,ˆf=Cf,f=C-1ˆf。其中:

b.模型实例
基于上述建模思路的一个LBGK模型的实例发表在文献[43]。那里所采用的DVM为图5(c)所示(20)式中v2=2v1=2c的情形。模型构建主要过程如下:
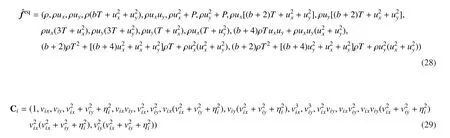
系数矩阵C的逆C-1可以使用软件Matlab解析求解。结果如下:其中,

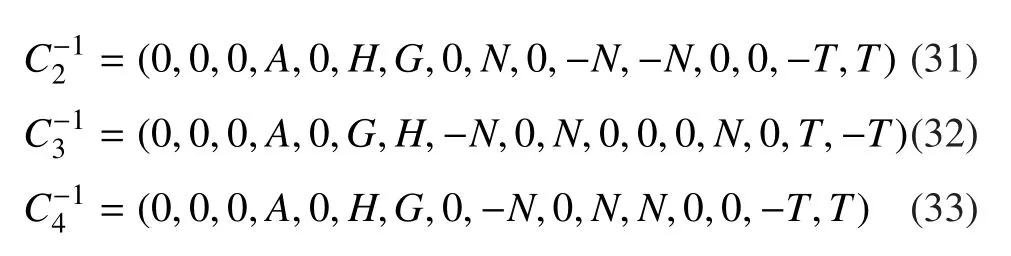

式中引入的系数如下:
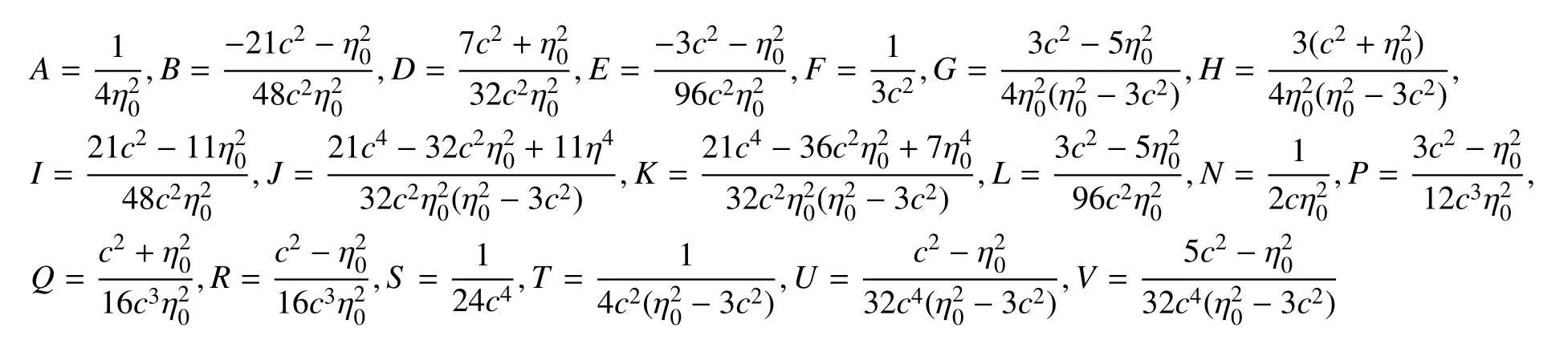
需要说明的是,对系数矩阵C解析求逆是节约运算量的关键技术。同时建议,在程序编写前,首先获得的解析表达式。在程序中直接使用的解析表达式进行计算。
下面,我们给出几个算例。我们考虑一维和二维黎曼问题。在LB模拟过程中,时间演化采用三阶隐式–显式Runge-Kutta有限差分方法计算,空间导数通过NND(The Nonoscillatory and Nonfree-parameter Dissipation)格式进行计算。第一个算例为两个强冲击波的碰撞问题。初始条件如下:

其中下标“L”和“R”标注左边和右边的宏观量,中间是一个强间断。通常认为这是一个难度较大的算例。其精确解包含一个向右传播的左冲击波、一个向右的接触间断和一个向右传播的右冲击波;并且,左侧冲击波向右侧缓慢传播,这给计算方法带来额外的困难。图6给出LB模拟结果和解析结果的比对。这里,t=0.08,γ=1.4,τ=4×10-5。结果表明,所构造的LB模型对冲击波和接触间断具有很好的扑捉能力。
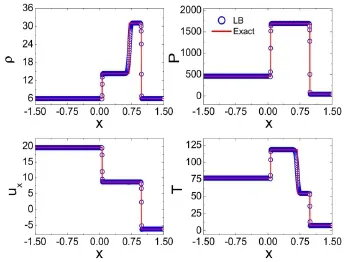
图6. LB模拟结果与解析结果的比较
第二个算例为Colella爆炸波问题。初始条件如下:

这也是一个挑战性较强的、检验数值方法的好算例。这个问题的精确解包含一个向左传播的稀疏波、一个接触间断和一个冲击波。图7给出了LB模拟结果和解析结果的比对情况。这里,t=0.018。这个算例说明,所构造的LB模型可以成功模拟的温度比和压强比高达105。第三个算例为冲击波的正规反射问题。图8给出一个Mach数为30的斜入射冲击波(与壁面夹角为25◦)在壁面发生正规反射的模拟结果。上图为密度轮廓图,下图为ux的轮廓图。这里,τ=2×10-5。模拟结果与解析结果一致。

图7. LB模拟结果与解析结果的比较
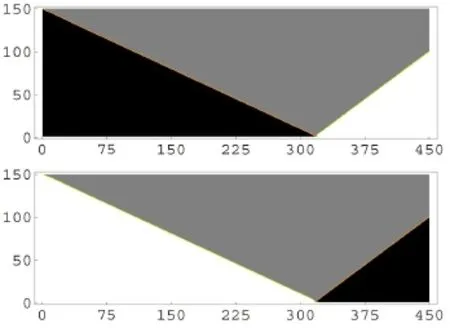
图8. 冲击波正规反射的LB模拟结果
2.MRT-LB动理学模型
系统中不同动理学模式趋于平衡的速率一般是不一样的。BGK模型中的松弛因子τ可视为所有动理学松弛过程松弛时间的一个平均值。随着系统Mach数、Reynolds数的升高,系统动力学行为越来越复杂,更多的动理学模式出现,不同动理学模式趋于平衡的速率之间的差异更加显著。系统的更合理描述需要多松弛时间(MRT,Multiple Relaxation Time)模型。在MRT-LB模拟中,首先,将碰撞操作在矩空间完成;然后,通过转置矩阵的作用回到离散速度空间;完成对流计算。MRT-LB模型可用下式描述:

一个MRT-LB动理学模型的构建需要如下三个步骤:(1)确定Maxwellian分布函数需要满足的矩关系,(2)构建离散速度模型,从而获得转置矩阵C,(3)对碰撞算符做小的修正以保证动理学过程的合理性。从形式上看,不同动理学矩趋于热力学平衡的速率可以由独立参数控制。但在物理上,有些动理学模式之间是存在耦合的。所以,需要通过Chapman-Enskog多尺度分析,与对应的宏观模型做比对以确定对碰撞算符某些分量的合理修正。
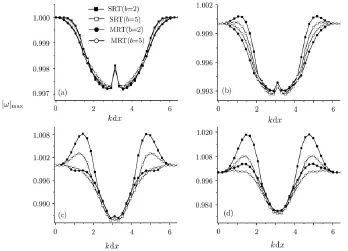
图9. LBGK与MRT-LB数值稳定性比较
说明:因为不同的松弛系数组合对应不同的动理学过程,所以可以通过重新组合矩关系而构建不同的MRT-LB动理学模型。通过这种方式获得的不同的MRT-LB动理学模型适用范围可能有重叠,但也会有不同,所以不能简单地相互取代。一个MRT-LB动理学模型的例子参见文献[45,200,201]。从物理描述上来讲,LBGK为MRT-LB的一个特例。只有MRTLB中所有松弛系数都与LBGK中相同时,两者才模拟同一个系统。但考虑到任何动理学模型都是对实际系统所做的简化,我们也通过图9说明:物理建模的改进也有助于LB模拟数值稳定性的提高。该图给出von Neumann数值稳定性分析结果。
在von Neumann稳定性分析中,我们把LB演化方程写成Fourier级数的形式。如果系数矩阵的所有本征值的绝对值都小于1,则该演化方程在模拟中是数值稳定的。分布函数fi(xα,t)和ˆfi(xα,t)可以写为如下两部分之和:

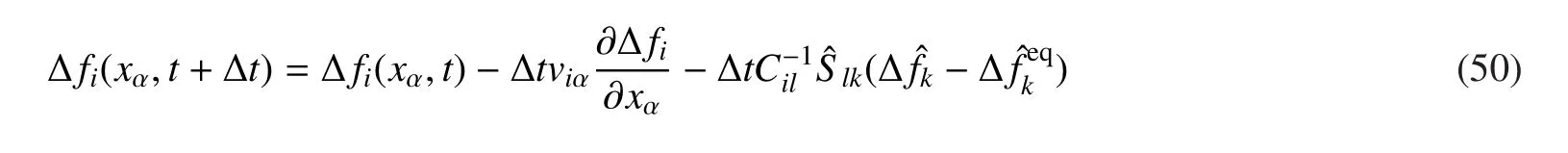

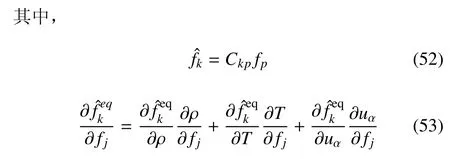
数值稳定性分析可以使用软件Mathematica来完成。在图9中给出的是文献[45]提供的MRT-LB动理学模型与其单松弛对应模型的数值稳定性比较。图中的横轴为k·∆x,纵轴为系数矩阵Gij本征值绝对值的最大值|ω|max。网格大小为∆x=∆y=10-3,时间步长为∆t=10-5。在单松弛时间(SRT)模型情形,松弛因子τ=10-5。其余参数如下:在图(a)中,(ρ,u1,u2,T)= (2.0,4.0,0.0,2.0),MRT-LB碰撞系数中s8=s9= 4×104,其余为105;在b=2时Mach数(Ma=为2,在b=5时Mach数为2.4。在图(b)中,(ρ,u1,u2,T)=(2.0,7.0,0.0,2.0),MRTLB碰撞系数中s10=5×104,s11=2×104,s13=1.5×104,其余为105;在b=2时Mach数为3.5,当b=5时Mach数为4.18。在图(c)中,(ρ,u1,u2,T)= (2.0,10.0,0.0,2.0),MRT-LB碰撞系数中s13=1.5×104,其余为105;当b=2时Mach数为5,当b= 5时Mach数为6。在图(d)中,(ρ,u1,u2,T)= (2.0,12.0,0.0,2.0),MRT-LB碰撞系数中s11=2×104,s13=1.5×104,其余为105;当b=2时Mach数为6,当b=5时Mach数为7.17。在图(a)所示低Mach数情形,MRT和SRT具有几乎相同的数值稳定性;但随着Mach数提高,二者的数值稳定性表现出明显差异。在图(b)和图(c)所示情形,MRT模型可以稳定模拟,但SRT模型却不能。当然,如果继续增大Mach数,该文献提供的MRT模型也会遇到数值不稳定性问题(例如图(d)所示);如果要获得稳定的数值模拟,离散格式(包括离散速度模型)等需要进一步调整。
用于恢复Navier-Stokes等宏观流体力学方程的MRT-LB研究也是近年来的研究热点之一[32,44,202~204]。这方面的文献很多,实际上这种类型的MRT-LB模型研究占据了目前已有MRT-LB文献的绝大多数。
D.LB动理学模型与非平衡效应
现在再回到LB模型构建过程中需要满足的7个矩关系:方程(9)~(15)。只有在前3个(即(9)~(11))中,可以用f(fi)取代而不引起任何问题。其原因是:前3个可以看作是密度、动量和能量的定义式,也可以看作是密度、动量和能量的守恒定律:系统在趋于或偏离热力学平衡过程中密度、动量和能量守恒。如果在后4个矩关系中用f(fi)取代则原等号两侧的物理量在数值上就可能不再相等。这个偏差描述的是系统偏离热力学平衡所导致的宏观效应,可以用来描述系统偏离热力学平衡的程度。为此,我们定义如下两种物理量:矩Mm与中心距


其中下标“3,1”表示三阶张量缩并为一阶张量,“4,2”表示四阶张量缩并为二阶张量。在二维笛卡尔坐标情形,矩M3,1(=M3,1αeα)是矢量,包含两个组分M3,1,x和M3,1,y;矩M2(=M2,αβeαeβ)是二阶张量,包含四个组分M2,xx、M2,xy、M2,yx、M2,yy,其中M2,xy=M2,yx,也就是说M2有三个独立变量同理,也只有三个独立变量是三阶张量,含有八个组分,其中只有四个独立变量中心距与矩Mm提供的信息互补。
下面,我们通过一些简单情形来理解一下上述动理学矩的含义。首先考察其几何含义。在概率论里,对于一维分布函数f(v),中心距
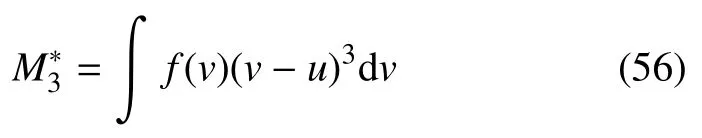
描述的是分布函数f(v)的“偏斜度”;中心距

描述的是分布函数f(v)的“扁平度”。对于Maxwellian分布(高斯分布或正态分布)函数
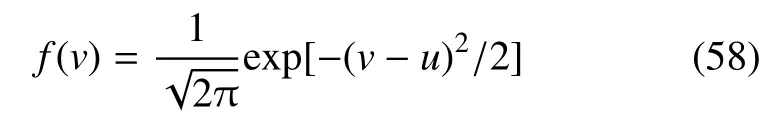
我们再来看其物理含义。M2、M3描述的是粒子涨落在不同自由度的2次和3次关联;M3,1是粒子涨落在不同自由度3次关联的一次缩并;M4,2是粒子涨落在不同自由度4次关联的一次缩并。矩M2和中心矩的迹都是守恒量,其迹的数值大小与温度密切相关;矩M2和中心矩的斜对角上的分量或元素与流体的剪切作用相关。矩M3和M3,1描述了两部分物理过程(系统宏观流动引起的能量通量和系统偏离热力学平衡所导致的“微观涨落能流”6目前所使用的物理学概念大都是描述平衡态系统的物理参数,而这里用于描述非平衡现象的高阶矩在流体力学中没有对应概念。本文使用的新概念与流体语言中的传统概念在微观机理上可能不同。)的叠加。中心矩和仅仅描述系统偏离热力学平衡所导致的“微观涨落能流”。当系统偏离热力学平衡态时,“微观涨落能流”不为0,矩M3、M3,1和中心距都不为0。另外,当系统处于热力学平衡态时,粒子速度分布函数满足对称性:f(v)=f(-v);而当系统偏离热力学平衡态时,该对称性不再满足,即f(v)≠f(-v)。为了描述系统偏离热力学平衡态的程度,我们引入两个非平衡效应量:
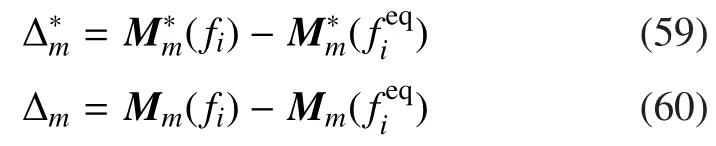
其中,下标m=2,3,(3,1),(4,2)。矩Mm和∆m同时包含宏观流动u和微观粒子热运动的信息,而中心距和则单纯描述了微观粒子的热涨落特征,其不同分量从不同角度描述或测量系统偏离热力学平衡的程度。通过对其各分量数值的分析,可以恢复真实分布函数中与我们最关心的宏观行为相对应的那部分最主要特征。到这里,我们可以看到,LBKM不仅可以在连续极限下恢复宏观流体力学方程,更重要的是,它为我们提供了一套描述或测量复杂系统偏离热力学平衡程度的方法。这是LBKM为非平衡统计物理学理论的贡献。
IV.LB应用实例
A.燃烧问题的LB建模与模拟
爆燃和爆轰是燃烧的两种不同的形式[205~207]。前者的反应区向前推进的速度小于声速,其能量传播方式主要是热传导和热辐射。后者的反应区向前推进的速度大于声速,其能量推进方式主要是冲击波。紧跟着化学反应的冲击波又称为爆轰波。爆轰现象广泛应用于工业生产和国防领域。例如,各种推进器的加速、采矿技术、表面喷层和设备清洗等。另外,在需要爆燃的环境(例如烟火晚会)发生意外的爆轰事件也将带来严重损失。所以,爆燃与爆轰相关的科学研究一直是个关注度很高的课题。
最近30年以来爆轰问题的模拟得到了迅速的发展。但两个技术问题仍在困扰着宏观建模。一是如何描述爆轰波阵面附近的非平衡行为,一是如何描述伴随反应放能过程的非平衡效应。因为宏观建模是基于平衡或近平衡近似的。由于LB模型基于非平衡统计物理中的基本方程—Boltzmann方程,在描述上述非平衡效应方面具有天然的优势[5]。
1.早期研究
在燃烧问题的LB建模与模拟方面,最早的尝试是由Sauro Succi等在1997年完成的[210]。他们在化学反应极快、热量释放率极低的冷火焰假设下模拟了甲烷和空气的层流火焰问题。在2000年Filippova等提出了一个杂化的LB模型[211,212]。其中流场使用LB描述,而输运方程、能量方程、组分方程使用传统的有限差分方法来描述。这是一个不彻底的LB模型,没有充分发挥LB潜在的优势。在2002年Yamamoto等发展了一个纯的LB燃烧模型[212]。但这个模型使用了两个分布函数。一个分布函数用于描述密度和流场,另一个用于描述温度场。三个物理场用两个分布函数来描述,这一与分布函数本身含义的不符给结果分析和模型的适用范围带来问题。2005年Yamamoto等使用LB模拟了三维多孔介质中的低马赫燃烧问题[214]。在这个工作中,他们仍使用双分布函数,一个分布函数用于描述压强和流速,一个分布函数用于描述温度和组分份额。在2006年Lee等就层流射流扩散火焰构造了一个近不可压LB模型[215]。以上所有的模型针对的都是近不可压系统,多数模型甚至忽略化学反应对流场的影响,这对爆轰问题的模拟是致命的。
2.我们的模型
在2013年初,我们课题组发表了第一个适用于爆燃和爆轰模拟的LB模型[39]。在该模型中,流体行为使用我们在2008年发展的一个高速可压LB模型描述[139],化学反应使用Lee-Tarver模型描述[216]。该模型实现了化学反应放能过程与流体动力学行为的自然耦合。Lee-Tarver模型是目前应用较多的反应率模型之一。Lee-Tarver反应率模型由两项构成:点火项和成长项。前者多用于研究各种热点的形成和随后的生长。后者多用于描述化学反应的成长过程。
作为这方面工作的第一步,我们首先考虑最简单的系统和最简单的模型:系统中只含有两种介质:反应物和产物,且化学反应不可逆。我们的模型可用下面方程组描述:
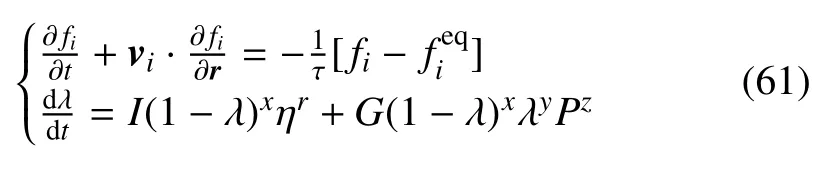
其中第一式为LB演化方程,描述流体流动;第二式为Lee-Tarver模型,描述化学反应进程。其中,λ为反应产物在所有物质中所占份额,η= (V0/V)-1为相对压缩度。V和V0分别为反应前后的比体积,与相应密度ρ的关系分别为V=1/ρ,V0=1/ρ0。I,G,x,y,z,r为模型参数,其中G,x,y描述的是反应率对燃烧面积等的依赖度。参数G也依赖于入射冲击波的压力。Pz描述的是局域压力对反应率的影响方式。作为这类LB模型构建的第一个例子,我们先考虑最简单情形的反应率模型:令x=y=1,a=Iηr,b=GPz。这样,Lee-Tarver模型简化为:

其中Tth为燃烧发生的临界温度。由于化学反应的速率比流动过程要快得多,所以成功模拟的一个关键技术为分裂算子思想的使用。从物理上,可将上述反应率方程理解为:反应产物所占份额的变化由两部分构成:(1)局域流动导致的变化,(2)化学反应导致的变化。即:

局域流动导致的变化使用一阶迎风格式计算:

化学反应导致的变化使用解析解:
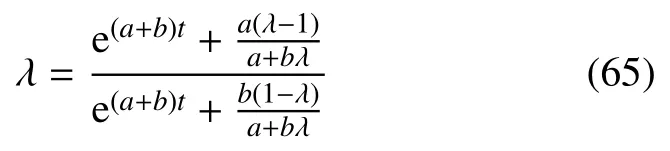
其中下标I-1,I,I+1为x-或y-方向的格点编号。在实际模拟中,化学反应放能过程与流动过程耦合的流程可用下式表示:

其中Q为单位质量反应物放出的热量。即:化学反应放热导致局域内能增加,局域内能增加导致局域压强增大,局域压强的增大进一步影响局域流场的行为。
这样,放能过程与流动过程实现了自然耦合。为了方便模拟内爆、外爆等问题,我们进而发展了一个极坐标下的LB爆轰模型[217]。

图10. 矩及其对平衡态值的偏离

图11. 矩及其对平衡态值的偏离
我们通过以下典型问题的模拟来完成对新构建模型的验证和确认:(1)冲击起爆典型问题:粘性爆轰的活塞问题,(2)热起爆问题,(3)爆轰波的规则与马赫反射,(4)爆轰波与冲击波的碰撞问题,(5)爆轰波引起的RM不稳定性问题。
3.爆轰过程中的非平衡效应初探
为了展示LB动理学建模相对于传统宏观流体力学建模的物理学优势,同时也作为LB模型研究爆轰问题非平衡效应的起步,我们首先研究最简单的一维稳定爆轰问题,并将注意力集中到von Neumann峰附近,研究与化学反应进程相关的热力学非平衡效应。
图10~图13给出一个典型的一维稳定爆轰波结构及其对应的矩关系和热力学平衡偏离量。具体参数参见原始文献[39]。图10~图13分别对应m=2,3,(3,1),(4,2)时的情形。其中的点对应的是由分布函数fi计算得到的结果,线对应的是由分布函数计算得到的结果。在每副图中,(b)和(d)分别对应Mm和(c)和(e)分别对应∆m和图(a)为一维稳定爆轰波的具体结构,在左右两侧重复出现,起到参考和便于对比研究的作用。由于爆轰波前导冲击的作用,密度、温度、压强和流速迅速增加并达到von Neumann峰值。在密度、温度和压强迅速增加的过程中,如果化学反应所需的条件阈值获得满足,则化学反应开始。在反应区内,化学反应进程(或产物在混合物中所占份额)参数λ从0增加到1。由于爆轰波的传播速度比纯冲击波要快,所以与纯冲击情形相比,爆轰波阵面后面的物质在反应过程中体积迅速膨胀,导致密度、压强、流速在反应区内降低。温度的变化情况比较复杂:一方面体积膨胀导致温度降低,另一方面化学反应所释放热量又使温度升高。所以,温度的最终变化取决于这两种机制的竞争。具体地说,它取决于状态方程和化学反应模型。应该指出的是,爆轰问题的很多传统模拟都是基于Euler方程的,都假设冲击波阵面的宽度为0,因此,密度、压力、温度、流速是瞬时达到von Neumann峰的。很显然,基于这个假设的模拟对于von Neumann峰附近的流场、状态演化描述是不够准确的。在我们的LB模拟中,可以清楚地观测到冲击波阵面的宽度,可以清晰地观测到各物理量的增长过程。在我们的模拟中,我们使用的是温度起爆条件,即系统温度达到起爆温度阈值时化学反应开始。我们可以看到,在绝大多数情形,在温度达到von Neumann峰之前,化学反应就开始了。如果化学反应所需的温度阈值升高,则化学反应起点向von Neumann峰靠拢;如果化学反应所需的温度阈值高于系统局域能够达到的最高温度,则化学反应不会发生,这时模拟得到的就是纯粹冲击波作用时的情形。Euler方程模拟所假设的从von Neumann峰开始起爆,只是个理想的特例。

图12. 矩及其对平衡态值的偏离
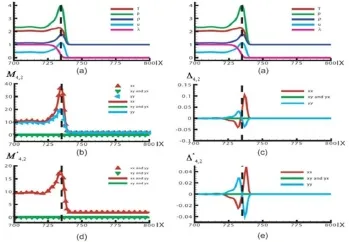
图13. 矩及其对平衡态值的偏离
由图10(b)和(d)可以看到,矩M2的xx分量最大,然后是yy分量,两个剪切分量(xy,yx)一直为零;而矩的xx和yy两个分量一致,两个剪切分量(xy,yx)一直为零。其原因为M2的xx分量中包含了宏观流速的贡献。分子热涨落对xx和yy两个分量的贡献相等;爆轰波的宽度很窄,不同自由度之间的耦合来不及发展。M2和给出的信息相同:xx分量和yy分量大小近似相等,符号相反;在von Neumann峰位置刚好为0,在von Neumann峰前后,它们以相反的方向偏离0值;在von Neumann峰前xx分量为正,yy分量为负;在von Neumann峰之前它们的幅度比峰后要高。这说明,考察到第4个矩关系时,在von Neumann峰位置系统已表现出偏离热力学平衡态的特征;在von Neumann峰前后,系统偏离热力学平衡的方向相反;且在von Neumann峰之前,温度梯度所在自由度的内能比横向自由度的内能大。由于温度、密度、压强在冲击波前沿上升速率比峰后下降速率要大,所以峰前偏离热力学平衡程度更高。
从图11可以看到,M3的xxx分量最大,然后是yyx,yxy,xyy分量,其余分量为0。由分布函数fi计算得到的∆3及同样具有这一特征。另外,由平衡分布函数计算得到的均为0。不为0的量均为相应物理量(x自由度和y自由度总能量或内能)在x方向的通量;且x自由度的总能量或内能通量较大。图11还给出一个重要信息:∆3及的xxx分量和yyx(yxy,xyy)分量在von Neumann峰位置不再为零,即考察到第5个矩关系时观测到更多的非平衡效应。第6个矩在量纲上对应能量通量,只有两个分量。图12中给出与图7一致的非平衡效应。第7个矩与第4个矩物理意义不同,但它们都有4个分量。图13中的结果可以按图10相同的方式进行分析。
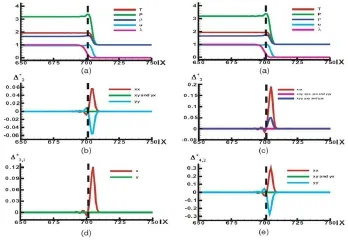
图14. 矩及其对平衡态值的偏离
图10~图13中的非平衡效应可以做如下解释:在密度、速度、压力、温度四个物理场中,任何一个宏观量的梯度都会引发热力学非平衡效应。在冲击作用过程中,冲击作用首先引起冲击方向这一自由度上的内能增加;通过分子碰撞(即热力学弛豫),使得这一自由度的部分内能逐渐转移到其余自由度;然后这一自由度的内能继续增加,同时向其余自由度上的能量转移也在继续,直至冲击作用结束。在von Neumann峰处,各个自由度上的内能达到基本均分。在von Neumann峰之后,化学反应释放的能量导致爆轰波速高于纯冲击波情形,相对于纯冲击波情形,化学反应区内的物质体积有所膨胀,于是压强下降。压强的下降(即稀疏作用)引起这一自由度上的内能下降;通过分子碰撞(即热力学弛豫),这一自由度逐渐接受来自其余自由度上的内能,同时这一自由度上的压强继续下降,进一步引起这一自由度上的内能下降,直至压强不再降低。各个自由度上的内能再一次达到基本均分,系统基本恢复到热力学平衡。这些过程可以在和曲线上获得理解。和的曲线表明,在von Neumann峰前,压强的继续上升(冲击作用),使得冲击方向上的“微观涨落能流”正向(冲击方向)偏离热力学平衡;在von Neumann峰后,压强降低,使得这一方向上的“微观涨落能流”反向偏离热力学平衡。相对于峰后的稀疏阶段,峰前压缩阶段的压强梯度更大,所以峰前的“微观涨落能流”偏离热力学平衡幅度较大。由于x、y方向的微观速度不相关,包含奇数个y分量的“微观涨落能流”分量始终为0。
图14给出粘性和热传导系数放大10倍后的热力学平衡偏离量∆∗m,m=2,3,(3,1),(4,2)。我们可以看到在这种情形,von Neumann峰是压强、密度、温度和粒子速度的共同的峰。在von Neumann峰系统刚好处于热力学平衡态。热力学偏离量在峰前或峰后的符号相反,且峰前偏离幅度较大。与图10~13相对比可见,粘性的另外一个效应就是使得系统在峰前和峰后偏离热力学平衡的幅度加大。
我们可以通过图11~图14中∆m的数值来进一步理解LBKM被称为“自适应”、“多尺度方法”的原因:(1)在远离界面的地方,∆m的数值基本为0,说明系统基本处于热力学平衡态,这时LBKM给出的结果自动与Navier-Stokes方程相符合;(2)在界面附近,∆m的数值明显不为0,说明系统偏离热力学平衡较远,这时LBKM给出的结果自动比Navier-Stokes方程描述要合理。在远离界面时的结果对应于暂时不考虑微介观结构情形下的大尺度行为(相当于放大镜倍数较低,视野较大时所看到的行为);在界面附近的结果对应于考察更精细时小尺度结构的效应(相当于放大镜倍数较高,视野较小时所看到的行为)。
4.小结
本工作给出一个适用于燃烧和爆轰模拟的LB模型。其中的流体流动通过我们以前发展的一个高速可压LB模型来描述,化学反应使用Lee-Tarver模型描述。由于化学反应的时间尺度一般比流动过程要小很多,所以成功模拟的一个关键技术为算子分裂方法。模型的有效性通过一些典型问题获得验证和确认。与Yamatomo的燃烧模型相比,这个模型实现了用一个分布函数同时描述密度、流速和温度三个物理场。与Filippova等和Lee等的模型相比,这个模型是含温度场的、可压的。与以前所有的LB燃烧模型相比,这个模型实现了化学反应放能和流动过程的自然耦合,不仅适用于低马赫数燃烧,同样适用于高速爆轰模拟。该模型构造的思路可以用于其它燃烧、爆轰LB模型的构造。这类LB模型可以用于研究燃烧与爆轰相关的一些复杂现象,特别是与界面相关的一些非平衡效应。
作为应用的一个实例,我们研究了一维稳定爆轰波问题。为了展现LB建模的优势,我们将注意力集中在反应区及其前后重点研究其中的非平衡行为。研究表明:一般情形下,化学反应区从von Neumann峰前开始,跨越von Neumann峰。在von Neumann峰之前只存在升温机制,在von Neumann峰之后,化学反应放热引起的升温与反应产物膨胀引起的降温机制并存。von Neumann峰不是温度的极大值点。温度的峰值一般在von Neumann峰之后。最大值点(峰值点)的不重合是系统无法完全恢复到热力学平衡的原因。系统粘性的增大有两个效应:一是是系统在von Neumann峰更加接近热力学平衡态,二是在von Neumann峰前后系统偏离热力学平衡的幅度加大。在反应速率极低的情形下,与纯粹冲击情形的区别是:从化学反应启动到跨过von Neumann峰,进一步到化学反应结束之前的这一较宽区域内,温度一直在升高。(温度从上升到最后的稳定,不存在极大值点。)所以,从冲击响应过程开始到化学反应结束,系统始终处在热力学非平衡态。在反应速率极高的情形下,在压强上升到von Neumann峰之前化学反应已经结束。在此情形下,von Neumann峰后不再有升温机制。
B.流体不稳定性的LB建模与模拟
流体不稳定性研究是惯性约束聚变点火研究的关键问题。另外,流体不稳定性问题同样广泛存在于武器物理、许多工业过程和自然现象当中。其研究具有重要的基础与现实意义。
由于流体力学不稳定性的非线性发展涉及强非线性、多尺度,以及湍流等老大难问题,所以理论研究进展缓慢。流体不稳定性的非线性发展导致流体界面的变形、破碎,直至湍流混合,是三维过程,对实验诊断技术要求较高。数值模拟是目前研究流体不稳定性的重要手段。
1.RM不稳定性研究
我们通过自己构造的MRT-LB模型研究了RM不稳定性前期的一些规律。我们考虑水平放置的激波管,管中左右两侧分别放置着密度不同的两种介质,初始界面为竖直平面,界面两侧密度不同,其余各量(压强和流速)相同;我们在界面上设置一个向左鼓起的密度扰动,加载的冲击波方向为从左向右。(1)当轻介质在左重介质在右情形,模拟结果给出如下物理图像:冲击波到达界面时发生透射和反射,透射波波前具有一定曲率。冲击波的压缩作用使得密度扰动幅度首先略微减小,压强界面由平面变得逐渐随着密度界面弯曲。这时,在密度界面左侧,由于反射波仍为压缩波而压强升高,扰动顶部的压强高于顶部两侧,所以部分物质粒子向两侧流动,从而使得扰动的幅度再次增加,逐渐形成重介质插入轻介质的“钉”状结构。随着物质粒子向顶部两侧流动,到某一时刻顶部的压强变得比密度界面右侧略低,这个与初始冲击波反向的压力差和当前的密度梯度导致“钉”状结构的顶部形成漩涡,进而最终形成“蘑菇”状结构。模拟得到的增长规律与Zhang-Sohn模型的预言定性一致,但在数值上增长率比Richtmyer模型更接近实验结果。(2)当重介质在左轻介质在右情形,模拟结果给出如下物理图像:冲击波到达界面时发生透射和反射,反射回稀疏波。密度扰动顶部重介质一侧的压强高于轻介质一侧。在压力差作用下,扰动幅度随着界面向右侧移动而减小,逐渐过渡到扰动的峰和谷相互转换。重、轻流体逐渐相互穿入对方区域从而形成“钉”和“气泡”。下面有两种可能的情形发生:(一)透射波继续向右移动,不再与界面发生作用;界面的扰动继续增加,最终形成蘑菇状。(二)透射波遇到右侧的固壁反射回向左的冲击波,再次与界面发生作用,从而形成冲击波的二次加载。随着二次加载,界面幅度再次首先被压缩,然后以高于二次加载前的速率增长。增长速率的增加是由于二次加载引起了新的漩涡[44,45,204]。
为了更加方便内爆、外爆等问题的模拟研究,我们需要发展基于曲线坐标的可压流体LB动理学模型。2013年初,我们在Watari极坐标模型的基础上发展了一个基于极坐标系的LB模型[144,145]。在该模型中,时间演化和空间演化通过引入算子分裂法的思路来处理(算符分裂法可看作是一种动理学模型)。其中时间演化通过解析解计算,空间演化通过一个修正的Warm ing-Beam格式进行运算。本模型不仅适用于模拟亚声速流体,也适用于超声速流体的模拟。为了展示LB模型在物理描述方面的优势,同时作为通过LB研究RM不稳定性演化过程中非平衡效应的开始,我们先选择最简单的情形,将注意力集中到力学界面和物质界面附近,研究由于系统偏离热力学平衡所导致的宏观效应。在外爆情形,为了同时获得冲击波阵面和稀疏波阵面,我们模拟研究冲击波由重介质向轻介质传播、遇到物质界面后产生透射冲击波和反射稀疏波的情形。
在内爆情形,分别模拟研究了冲击波在环形区域和圆形区域中向内传播过程中物理量的变化规律,并通过离散速度分布函数的速度矩分析了冲击波波阵面附近的非平衡效应。为了从更基本层面理解界面行为,给出了波阵面处真实粒子速度分布函数在速度空间的示意图[145]。下面简单介绍我们极坐标LB模型的部分验证与模拟。
a.验证与确认
当冲击波稳定传播时波前和波后的物理量满足雨贡纽(Hugoniot)关系:
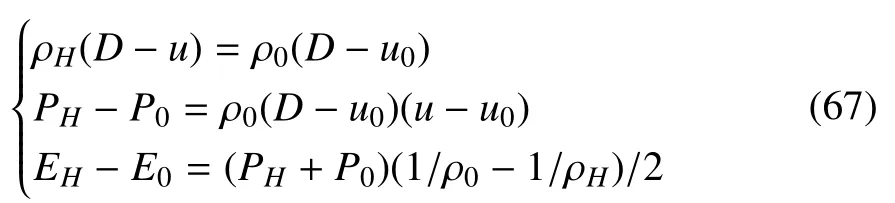
其中下标0和H分别表示冲击波波前和波后的物理量,D为冲击波的传播速度。如果波前和波后的状态方程满足理想气体状态方程:

那么公式(67)中的能量方程可写成:
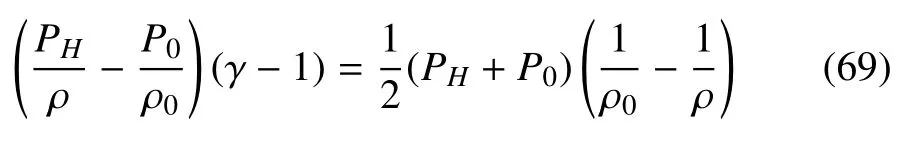
a.1计算区域为环形
内外半径分别为R1=2000,R2=2002的环形物理区域内,冲击波由外向内传播,波速D=2,初始时刻的物理场为:
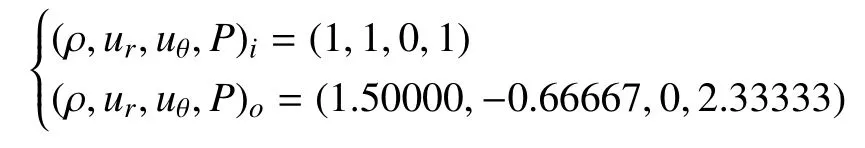
这里下标i表示2000≤r<2001.6,该部分为冲击波波前区域,下标o表示2001.6≤r≤2002,该部分为波后区域7初始条件给出的是强间断的物理场,而实际的冲击波波阵面是一个光滑过渡层,因此在数值模拟的初始阶段物理量分布不光滑。在数值模拟一段时间后,冲击波将稳定传播,物理量也会光滑分布。然后,我们可以截取冲击波稳定传播时的物理场作为初始条件再次进行数值模拟。,波阵面前后的物理量满足雨贡纽关系(67)。计算网格为Nr×Nθ=2000×3。
图15为冲击波在环形区域向内传播过程中物理量沿径向的一维分布图,模拟得到的波后物理量为(ρ,T,P,ur)=(1.50031,1.55593,2.33437,-0.66686),相对于初始时刻的波后物理量分别增加了(0.2‰,0.2‰,0.4‰,0.3‰)。考虑到环形区域的几何效应,冲击波波后区域的物质随着时间演化将不断聚集压缩,数值模拟得到的波后参数应该比初始条件高一些。
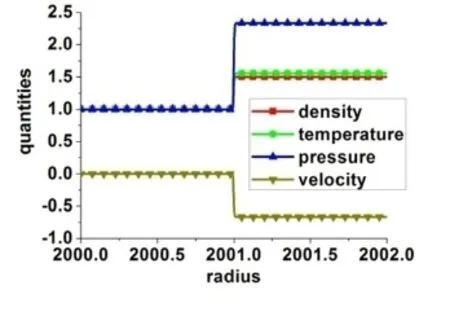
图15. 冲击波在环形区域向内传播时物理量沿径向的分布图
a.2圆形区域
在半径为R=1的圆形区域,冲击波以波速D= 2向内传播,初始时刻的物理场为:
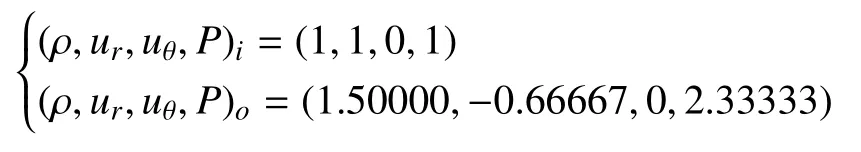
这里下标i表示区域0≤r<0.8,下标o表示区域0.8≤r≤1。计算网格为Nr×Nθ=1000×3。图16为冲击波在圆形区域传播过程物理量沿径向分布的演化图,选择的时刻分别是t=0.000,0.200,0.345,0.500。
在初始阶段,冲击波向内传播,波后区域的物质具有方向向内的宏观速度,由于惯性作用波后不断有物质涌入,该区域的物质不断被挤压,密度、温度和压强不断上升;同时,被挤压的物质将相互排斥,在斥力的作用下波后区域的这部分物质的速度将不断下降。需要说明的是,在冲击波向内过程,波阵面附近的温度不断上升,冲击波的波速不断加快,见图16(c);当t=0.345时,冲击波到达原点,此时的密度、温度、压强的大小在径向单调分布,极点附近的数值最大,向外依次递减,见图16(a)、(b)和(d);冲击波向外传播时,波后区域的物质具有向外的宏观速度,在原点附近的速度最小,在波阵面处的速度最大。波前区域物质的宏观速度指向内,并且该部分物质的速度不断减小,而密度、温度、压强不断上升。
b.非平衡效应研究
b.1非平衡效应的宏观表现
例如图15,在冲击波稳定传播过程,波前的物理系统处于平衡态,波后的物理系统也将很快达到新的平衡态,而波阵面附近的非平衡效应则表现的比较明显。图17给出了对应于图15所示冲击波波阵面附近的中心距在径向的分布图。这里只给出了各个中心距的独立变量。从图17可以看出以下几点:第一,图(b)、(d)、(f)、(h)中显示的数值都比较小,数量级是10-3,这说明我们所研究的非平衡系统偏离平衡态的程度并不是很大;第二,图(c)中的与图(d)中的的图像一样,图(e)中的与图(f)的图像一样。这是因为在理论上故第三,图(b)中与的大小相等,正负号相反,即这是因为与的物理量纲分别对应r与θ自由度上的内能,而与分别表示非平衡系统在r与θ自由度上偏离能量均分状态的程度8能量均分定理描述的是平衡态系统的物理规律,处于非平衡态的物理系统在各个自由度的内能不一定均分。。第四,在图(d)、(f)、(h)中的峰值最大,而的数值接近于零。这是因为它们的物理量纲都与“能量涨落能流”有关。由于冲击波的冲击作用,波阵面附近的物质粒子在速度空间分布的对称性将得到破坏,系统在r自由度上将存在较大的“能量涨落能流”,而在θ自由度上基本上没有“能量涨落能流”。

图16. 冲击波在圆形区域内传播时的物理量沿径向分布的演化图:(a)密度,(b)温度,(c)速度,(d)压强

图17. 冲击波在环形区域向内传播时M∗与∆∗在径向的数值分布。图(a),(c),(e),(g)中分别为为M,M,M,M,图(b),(d),(f),(h)分别为∆M,∆M,∆M,∆M
b.2非平衡效应的微观机制
在冲击波波阵面附近,系统非平衡效应的演化过程可以解释如下:冲击波是一个能量传播的过程,在冲击波附近会产生较大的宏观物理量的梯度。在冲击波作用下,物质粒子在r自由度上的能量(包括动能、内能)首先得到增加,然后这部分变化的内能将通过分子间的碰撞传递到θ自由度。同时,r自由度的内能在冲击波作用下继续升高,如此往复,直到宏观物理量的梯度完全消失,系统在各个自由度的能量均分,系统将达到新的热力学平衡。

图18. 真实分布函数和Maxwellian分布函数在速度空间vr与vθ的一维示意图。f(vr)、f(vθ)与feq分别用长划线、短划线和实线表示
图19. 真实分布函数在速度空间vr,vθ的投影轮廓示意图
图20. 真实分布函数在速度空间vr,vθ的三维分布示意图
2.KH不稳定性研究
在过去的几十年,人们通过理论、实验和数值模拟对KH不稳定性进行了广泛的研究。研究表明KH不稳定性的演化速率依赖于密度比、粘性、表面张力等因素。但传统流体力学的相关研究主要局限于无粘性、无热传导、弱可压、不含表面张力的情形。陈十一课题组[218]曾使用不可压流体LB模型对KH不稳定性进行研究。由于实际流体均存在不同程度的可压性,我们构造了一个二维十九速(D2V19)LB模型,这个模型在连续极限下对应可压流体系统的Euler方程。并通过该模型对KH不稳定性进行了更深入的研究。在该模型中,LB方程的对流项采用具有5阶精度的WENO格式进行求解,从而使得界面附近的非物理震荡获得了有效的降低。我们重点关注了速度梯度和密度梯度对KH不稳定性发展的影响。数值模拟中得到了尖锐、光滑的密度等值线。
我们研究速度梯度对KH不稳定性演化过程的影响。初始构型如下:
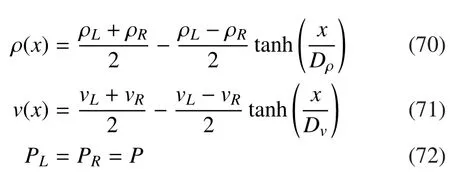
其中Dρ和Dv分别为密度和速度过渡层的宽度。ρL= 5.0(ρR=2.0),vL=0.5(vR=-0.5),PL(PR)=2.5,左右两侧的Mach数分别为0.5和0.32。计算区域的长宽分别为0.6和0.2,划分网格数为600×200。在x方向施加一个单模速度扰动:
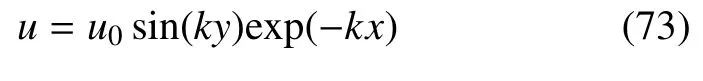

图21. 密度场的时间演化过程
其中u0=0.02,k=10π。在y方向使用周期边界条件。在x方向使用出流(零梯度)边界条件:
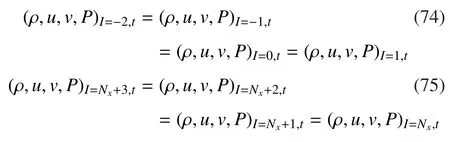
其中I=-2,-1,0,Nx+1,Nx+2,Nx+3为虚拟网格点。
图21给出了Dv=4、Dρ=8情形4个时刻的时间演化图。可以清楚地看到,在时刻t=0.3时,界面已经开始在初始扰动和切向速度差的作用下发生可观测的扭曲变形。在线性增长阶段过后,在围绕初始扰动位置形成了一个完好的涡旋。在时刻t=0.7涡旋进一步变大。在初始界面附近的混合已经开始。界面连续、光滑,进一步验证了LB模型捕捉界面变形的能力。为了定量描述混合层或涡旋的特征,我们在图22中给出了t=0.1,0.3,0.5,0.7四个时刻密度轮廓的曲线。密度轮廓从简单光滑逐渐变化到不规则。可以见到,混合层的厚度和密度扰动的幅度随着时间再增大。密度轮廓曲线上的锯齿形部分体现了流体从密度大的区域向密度低的区域流动和混合层内的不规则性。
为了考察速度梯度效应,我们模拟了不同速度过渡层宽度Dv的情形。在图23中给出的是t=0.6时刻Dv=4,8,12,16时的密度场。可以看到,速度过渡层的宽度对KH不稳定性的演化具有明显的影响。在固定密度梯度和速度差值大小的情形下,速度过渡层越宽,KH不稳定性越弱,涡旋出现得越晚。在图23(a)和(b)中,大的涡旋的出现表明,演化已经进入强非线性阶段。然而,在图23(c)和(d)中,混合层的宽度由于速度过渡层的增宽而迅速下降,演化仍在弱非线性阶段。图23(a)~(d)的结果还表明,速度过渡层对KH不稳定性具有致稳作用。

图22. 四个时刻密度轮廓的曲线
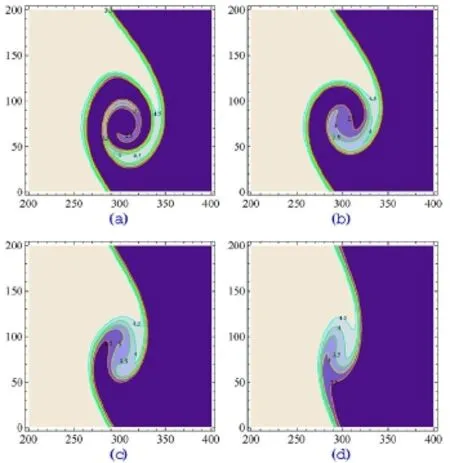
图23. 四种不同速度过渡层宽度时的密度场
在KH不稳定性发展的早期,扰动幅度A按照如下的线性微分方程演化:
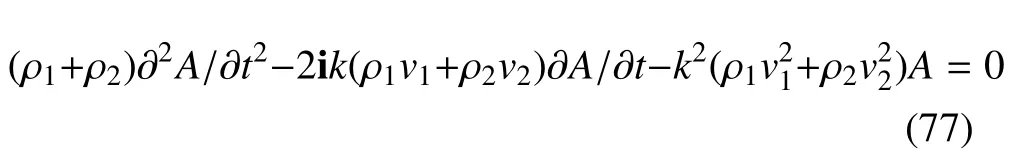
也就是说,扰动幅度随时间指数增长:A(t)=A0eγt,其中γ为增长系数。如果在对数–线性图上描述扰动动能峰值Ex=0.5ρu2随时间演化,那么这个指数增长就表现为线性行为(见图24)。所以,也可以通过在这个图上线性拟合线性增长阶段来得到增长因子γ。我们注意到,Ex∝u2∝(eγt)2的增长速率是KH不稳定的两倍,即k=2γ,其中k为线性拟合的斜率。动能Ex的峰值部分体现两种流体相互作用的强度。在图24中可见,扰动动能的对数首先随时间t线性增长,然后逐渐进入一个非线性饱和阶段。在固定密度过渡层和速度过渡层宽度的情形下,在线性阶段Ex随时间t逐渐增长。然而,速度过渡层越宽,Ex的值越小。这表明,速度过渡层越宽,密度场演化越缓慢。更进一步,我们发现,线性增长率γv对Dv的依赖性近似满足下面拟合关系:
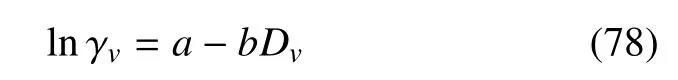
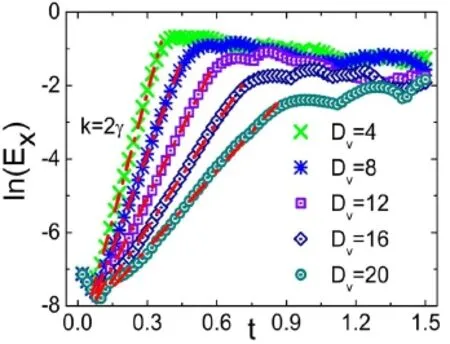
图24. 扰动动能对数随时间的演化
其中a=2.70,b=0.07(见图21)。在经典情形,线性增长率为:

其中∆u为切向速度差。速度过渡层越宽,相邻流体层的速度差就越小,从而线性增长率就越小,线性增长阶段的时间tlin就越长。
下面我们研究密度过渡层对KH不稳定性的影响。初始构型取为:(ρL,vL,PL)= (5.0,0.5,1.5),(ρR,vR,PR)=(1.25,-0.5,1.5)。参数如下:d x=d y=0.002,τ=10-5。图26给出了扰动动能峰值Ex随密度过渡层宽度演化的情形。可见,在速度过渡层宽度固定、密度差值固定的情况下,线性增长率随着密度过渡层宽度Dρ的增加而增加。但是,当Dρ>6时,线性增长率不再发生显著的变化,见图27。这表明与速度过渡层相比,密度过渡层的有效作用范围要小。当Dρ<6时,线性增长率γρ对Dρ的依赖关系可近似拟合为:

图25. 线性增长率随速度过渡层宽度的演化

图26. 密度过渡层宽度对扰动动能演化的影响

其中c=5.28,e=0.62(见图27)。在经典情形下,

其中A=(ρ1-ρ2)/(ρ1+ρ2)是Atwood数。密度过渡层越宽,相邻流体层的Atwood数就越小,从而线性增长系数就越大。所以,密度过渡层具有强化KH不稳定性的作用。
在实际流体中,密度过渡层和速度过渡层往往同时存在。下面我们来研究两者的综合效应。为此,我们引入一个比例系数R=Dρ/Dv。在图28中我们给出了R=0.5,1,2,5时的线性增长率随密度过渡层宽度的演化曲线。由图28可见,从整体上看,密度过渡层和速度过渡层的综合效应是减小线性增长率。只是在Dρ较小且R>1时出现二者综合效应增大线性增长率现象。这表明,从整体上来讲,速度过渡层的有效作用范围比密度过渡层要大。对于固定的R(>1)值,当Dρ较小时,相邻流体层间动能的输运效率由于密度梯度的增加而降低,所以线性增长率随着Dρ的增加达到一个峰值。当Dρ进一步增大时,速度过渡层的致稳效应逐渐占优势,从而导致线性增长率逐渐降低。当R<1时,在我们的数值实验范围内,线性增长率随着Dρ的增加单调减小。

图27. 线性增长率对密度过渡层宽度的依赖性
研究表明,KH不稳定性随着速度转变层宽度Dv的增大而减弱,随着密度转变层宽度Dρ的增大而加强。在暂态过后涡旋结构形成前,线性增长阶段的增长率γv与Dv的关系为:

增长率γρ与Dρ的关系为:
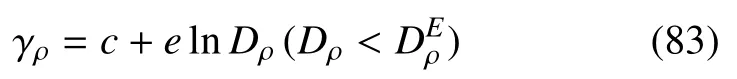

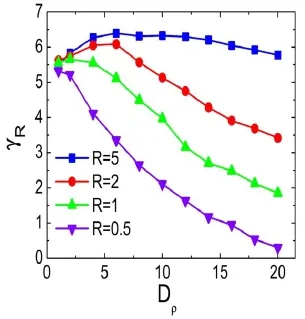
图28. R值对线性征率随密度过渡层演化的影响
速度转变层变宽导致∆u减小,所以γC减小;密度转变层变宽导致Atwood数A变小,所以导致γC增大。在实际应用过程中,可以联合使用速度梯度和密度梯度两种效应来稳定KH不稳定性。
3.RT不稳定性研究
RT不稳定性发生的物理条件是加速度由高密度物质指向低密度物质,例如:(1)在重力场中轻介质在下重介质在上,或者(2)轻介质推动重介质。在这种情况下,系统不处于能量最低状态,因而在力学上是不稳定的,必须释放出过多的势能,使系统回到最低能量的平衡状态。高密度物质和低密度物质通过交换位置,释放势能。如果能量释放过程很剧烈,会产生湍流混合。
RT不稳定性现象最初是由Taylor在1950年明确提出的。其实人们以他的名字来命名这个不稳定性之前,Rayleigh在1900年以及Lamb在1932年也都在某种程度上提及这个问题,因此这个不稳定性也经常称为Rayleigh-Taylor不稳定性或者Rayleigh-Lamb-Taylor不稳定性。Taylor的理论被Lew is的实验所证实,他明确地提出RT不稳定性发展的前三个阶段,后面的两个阶段被Birkho ff给出,RT不稳定性发展的五个阶段为:(1)线性阶段或小扰动阶段。在这个阶段中,线性化理论是适合的,扰动的幅度远小于扰动的波长,扰动按指数形式增长。扰动的界面逐渐变成上钝下尖的形状,上钝部分称为“气泡(bubble)”,下尖部分称为“尖顶(spike)”。(2)规则的非线性阶段。这时明显的气泡—尖顶形状结构形成气泡。(3)变形阶段。这时非线性作用开始显著,原先上下相似的谐波形状以常速度沿重力场的反方向进入重流体内部,尖顶以定常加速度沿重力场方向进入轻流体内部。(4)不规则的非线性阶段。这时在尖顶表面附近,两侧流体沿表面的速度的差异增大,KH不稳定性开始作用,在尖顶的头部会形成翻滚的“蘑菇”形状结构。(5)湍流混合阶段。这时界面两侧的流体在界面附近互相渗透,相互混合,大量的高次谐波被激发,混合区的宽度与初始扰动的特征波长没有关系。
关于第一个阶段的工作进行了很多,理论分析、数值模拟和实验结果互相吻合很好。关于第二个阶段,Haan、Jacobs和Catton用弱非线性理论对平面几何中的情况进行了分析,很好地描述了非线性的产生过程。而后面的阶段,很难进行理论分析,大部分工作需要依靠数值模拟进行分析。
历史上最早使用格子气或LB来研究RT和KH不稳定性的工作是由Gunstensen和Rothman在1991年完成的[219]。他们构建了一个满足伽利略不变性的格子气模型。这个模型通过引入大量的静止粒子来实现碰撞过程中的半细致平衡。这个模型在一定Reynolds数范围内给出合理的结果。作为模型的应用实例,他们模拟了不相容两相流系统中的RT不稳定性。所获得的界面扰动幅度在线性阶段的增长率随波数的变化关系和线性理论预测的结果符合较好。1998年聂小波、钱跃竑、Doolen和陈十一采用等温、低速、近似不可压、双分布函数LB模型模拟了两组分不相容流体的RT不稳定性[220]。两种组分分别用两个分布函数来描述。所获得的结果与实验、理论和其它模拟结果相吻合。1999年He等构造了一个等温、近似不可压、双分布函数、二维多相流模型[105]。其中,一个分布函数用于描述压强和速度场,另外一个分布函数用以描述密度场。对密度场的描述是通过对两组分的配额的描述来实现的。在两个分布函数的演化方程中都包含了一个描述分子间相互作用力的项。这里的配额参数可以作为一个指标函数用以追踪界面。这个模型能够捕捉尖锐界面,适用于低密度比多相流模拟。他们使用该模型模拟了二维RT不稳定性。在单模扰动情形,所获得的扰动幅度线性增长率和后来的汽泡运动速度都和理论结果及以前的模拟结果相符;在多模扰动情形,所得混合层的增长速度与以前的模拟结果相符合。他们还获得了一些可能是由于KH不稳定性介入引起的结果。随后该模型被扩展到三维[221]。Zhang等人采用He等人的LB模型[105]模拟了含表面张力效应的RT不稳定性问题[222]。Clark使用He等提出的LB模型研究了二维RT不稳定性问题,发现初始条件的微小变化就可引发混合层厚度增长率的较大变化。所以,作者通过一组不同初始条件的数值实验来研究了RT混合层的统计性质,确定了混合层增长率,同时也发现混合层将达到一种近似自相似的状态[223]。Chiappini等人采用Lee等人构造的LB模型[224~227],重现了不同Reynolds数下重力驱动的RT不稳定性现象[228]。李庆等人通过引入附加界面力给出一个修正的等温、低速近似不可压、双分布函数多相流LB模型,数值模拟中包含了RT不稳定性等现象[229]。在这个改进的模型中,一个分布函数用以描述密度场,另一个分布函数用以描述压强和流速场。Zu等人构造了一个基于相场的等温、不可压、双分布函数LB模型[230]。在这个模型中,一个分布函数的演化方程用以恢复不可压Navier-Stokes方程;另一个分布函数的演化方程用以追踪界面,它可以恢复Chan-Hilliard方程。在这个模型的算例中包含了RT不稳定性的部分结果。
前面几种模型均为等温、不可压模型。Liu等人构造了双分布函数不可压LB模型,数值研究了混合流体RT稳定性的Prandtl数效应[231]。在这个模型中,一个分布函数用以描述密度和速度场,另外一个分布函数用以描述温度场。2009年,Sbragaglia等人针对热流体动力方程Fourier-Navier-Stokes方程[232]:

建立自适应可压LB模型(简称SBBCSS模型),在该模型中Prandtl数不可调。与文献中其它RT不稳定性的LB研究工作相比:其它绝大多数LB模型为等温、低速、近似不可压模型,SBBCSS模型是温度自适应的、可压模型,既适用于低速近似不可压流体,又适用于高速可压流体系统。通过SBBCSS模型可以研究温度、可压性、流速等RT不稳定性发展的部分影响。而后该团队应用该模型做了一系列工作:Scagliarini等使用SBBCSS模型模型模拟Rayleigh-B´enard流体系统从静止到对流的转变过程。LB结果与解析结果和传统有限差分方法所得结果一致。同时,模拟结果显示,产生对流需要一个临界温度梯度。当温度梯度小于该临界梯度时,系统行为以热扩散为主;当温度梯度高于该临界值时,系统行为以动力学为主。换句话说,提高该临界温度梯度有利于抑制RT不稳定性演化过程中混合层的增长。他们数值确定了Atwood数到0.4、Rayleigh数到2×1010范围内非对称混合层的增长率[233];Biferale等基于SBBCSS模型,从方法角度和物理角度研究了二维RT不稳定性。在稳定进行的数值模拟中,空间分辨率达到4096× 10000,Rayleigh数达到1011。对四个量级范围内的速度涨落和温度涨落进行了逐级研究。他们的数值结果支持类Bolgiano惯性标度律的存在[234];Scagliarini等使用SBBCSS模型,研究了层流化效应和可压缩效应对RT湍流动力学的影响。他们测量了混合层内密度和温度涨落的PDF(Proability Density Function,概率密度函数),发现:这两个统计量在Atwood数较小(压缩性可忽略)时几乎没有区别,但在Atwood数较大(可压缩性较大)时具有显著差别[235]。Biferale等在超级计算机QPACE上实现了基于SBBCSS模型的RT不稳定性模拟,使用分数维数的概念研究了界面的一些统计特征[236];在模型中再引入简单的反应过程描述:冷、热流体之间的反应通过在温度方程中添加Fisher-Kolmogorov-Petrovsky-Piskunov源项来实现,反应热首先影响局域温度,然后影响非平衡分布函数,进而影响系统演化。研究了不同反应率下湍流混合与反应过程之间的竞争,以及湍流混合与波前传播之间的相互影响[237];他们进一步将模型改进,研究了强层流化和弱层流化环境下RT不稳定性引发的湍流对流问题[238]。
目前关于RT、KH与RM等流体不稳定性演化过程中的极其丰富与复杂的非平衡效应研究正处于起步阶段[239]。
V.总结与展望
材料物理、工程物理领域存在大量的非平衡、多相等复杂系统、复杂行为。LB起源于复杂系统复杂行为研究的格子气、元胞自动机模型;现代版的LBKM植根于非平衡统计物理学的基本方程—Boltzmann方程。除了可以在连续极限下恢复Navier-Stokes等宏观流体力学方程外,LBKM已经发展成为一种全新的、复杂系统非平衡行为的描述方法和模拟手段;通过LBKM结果我们可以获得真实分布函数中与我们关心的宏观行为关系最密切的那部分特征和性质。这是LBKM对非平衡统计物理学基本描述方法的贡献。可以通过宏观量研究系统的非平衡行为、可以提供系统偏离热力学平衡引发的宏观效应是LBKM建模优越于宏观连续介质建模的地方。
除了常见的复杂流体之外,LB方法同样适用于连续介质建模失效的高Kn数流体系统;LB方法已被推广应用于晶体生长动力学、半导体动力学、固体力学、声子动力学、金属泡沫生长动力学、裂纹生成与发展动力学、玻色–爱因斯坦凝聚等领域;LB思想已被移植应用于量子力学、电动力学、量子场论,为学科建设提供了新的思路;LB技术已启发产生了正在兴起的LFP(Lattice Fokker-Planck)技术。如果将LB视为求解偏微分方程的新思路,那么LB适用的范围几乎含盖了我们所关心的绝大多数物理系统(因为几乎所有物理系统的演化都遵循偏微分方程)。除了LB建模的一些思想,LB应用过程中发展起来的一系列数据处理技术、特征尺度提取技术、结构分析技术,有不少可以直接用于各类复杂构型、动态物理场的数据处理与特征分析。
LBKM将在各类非平衡流体、复杂流体局域非平衡效应方面有更多的贡献!除了可以从更基本的层面理解相应物理系统的特征、机制和规律外,这类研究结果可以为现有程序或软件中宏观模型的改进(例如修正项的构造)提供物理参考。
致谢
本文主要内容曾在亚美尼亚DSFD2013国际会议上作为邀请报告、在北京九所“学习、提高、创造”学术论坛、中科院过程工程研究所、中科院理论物理研究所、中国工程物理研究院流体物理研究所、北京大学、清华大学、北京师范大学、中国计量学院流体检测与仿真研究所、北京理工大学等作为专题学术报告介绍过。感谢陈式刚院士、朱建士院士、贺贤土院士、应阳君、方海平、陈晓松、郑伟谋、周善贵、周海军、汪秉宏、何大韧、赵鸿、刘宗华、郑波、王新刚、郑志刚、郭文安、邓友金、童培庆、晏世伟、王沫然、雍稳安、徐远清、王利民、王成、涂展春、陈勇、黄吉平、吴枝喜、吴金闪、占萌、张子柯、杨超、雍玉梅、钱跃竑、单肖文、郭照立、冉政、许友生、苏中地、倪国喜、甘延标、陈锋、林传栋、闫铂、董银峰、赖惠林、严微微等的讨论和宝贵建议。
本工作得到国家自然科学基金[批准号:11074300和91130020]、国家重点基础研究发展计划[批准号:2013CBA01504]、中国工程物理研究院发展基金[批准号:2012B0101014、2011A0201002]、爆炸科学与技术国家重点实验室开放基金[批准号:KFJJ14-1M]、理论物理国家重点实验室(中国科学院理论物理研究所)开放课题[批准号:Y4KF151J1]和计算物理重点实验室基金的资助。
参考文献
[1](俄)奥尔连科主编,孙承纬译.爆炸物理学[M],北京:科学出版社,2011
[2]Dewald E L,et al.Phys.Rev.Lett.,2013,111(23):235001
[3]春雷主编.核武器概论[M],北京:原子能出版社,2000
[4]许爱国,张广财,李华,朱建士等.材料动力学的介观模拟(北京应用物理与计算数学研究所讲义),北京,2011
[5]Xu A G,Zhang G C,Gan Y B,Chen F,Yu X J.Front. Phys.,2012,7(5):582
[6]Succi S,The lattice Boltzmann equation:for fl uid dynamics and beyond,Oxford University Press,London,2001
[7]郭照立,郑楚光.格子Boltzmann方法的原理与应用,北京:科学出版社,2009
[8]何雅玲,王勇,李庆.格子Boltzmann方法的理论及应用,北京:科学出版社,2009
[9]B¨osch F,Karlin I V.Phys.Rev.Lett.,2013,111:090601,
[10]Araki T.Phys.Rev.Lett.,2012,109(25):257801
[11]Dammone O J,Zacharoudiou I,Dullens R P A,Yeomans J M,Lettinga M P,Aarts D G.Phys.Rev.Lett.,2012, 109(10):108303
[12]Biferale L,Perlekar P,Sbragaglia M,Toschi F.Phys.Rev. Lett.,2012,108(10):104502
[13]Hickey O A,Holm C and Harden J L,Slater G W.Phys. Rev.Lett.,2010,105(14):148301
[14]Kunert C,Harting J,Vinogradova O I.Phys.Rev.Lett., 2010,105(1):016001
[15]Mendoza M,Boghosian B M,Herrmann H J,Succi S. Phys.Rev.Lett.,2010,105(1):014502
[16]Nash R W,Adhikari R,Tailleur J,Cates M E.Phys.Rev. Lett.,2010,104(25):258101
[17]Frydel D,Diamant H.Phys.Rev.Lett.,2010,104(24): 248302
[18]Frisch U,Hasslacher B,Pomeau Y.Phys.Rev.Lett.,1986, 56(14):1505
[19]聂小波.模拟可压缩流体的二维格子气模型,应用物理与计算数学研究所硕士学位论文(导师:陈式刚),北京, 1988
[20]Chen S,Chen H,Martinez D,Matthaeus W.Phys.Rev. Lett.,1991,67(27):3776
[21]Chen S,Doolen G D.Annu.Rev.Fluid Mech.,1998,30(1): 329
[22]Qian Y H,d’Hum ieres D,Lallemand P.Europhys.Lett., 1992,17(6):479
[23]Qian Y H,Deng Y F.Phys.Rev.Lett.,1997,79:2742
[24]Qian Y H,Chen S Y.Phys.Rev.E,2000,61(3):2712
[25]Qian Y H,Zhou Y.Phys.Rev.E,2000,61(2):2103
[26]Zhang R Y,Chen H D,Qian Y H,Chen S Y,E ff ective volumetric lattice Boltzmann scheme,Phys.Rev.E,63(5), 056705,2001
[27]Shan X W,Chen H D.Phys.Rev.E,1993,47(3):1815
[28]Luo L S,Lattice-gas automata and lattice Boltzmann equations for two-dimensional hydrodynam ics,Ph.D thesis, Georgia Institute of Technology,1993
[29]He X Y,Luo L S.Phys.Rev.E,1997,55(6):R6333
[30]Fang H P,Lin Z F,Wang Z W.Phys.Rev.E,1998,57(1): R25
[31]Lallemand P,Luo L S,Phys.Rev.E,2000,61(6),6546
[32]Lallemand P,Luo L S,Phys.Rev.E,2003,68(3):036706
[33]Luo L S,Girimaji S S.Phys.Rev.E,2003,67(3):036302
[34]Xu A G,Gonnella G,Lamura A.Phys.Rev.E,2003,67(5): 056105
[35]Xu A G,Gonnella G,Lamura A,Amati G,Massaioli F. Europhys.lett.,2005,71(4):651
[36]Xu A G,Gonnella G,Lamura A.Physica A,2004,331(1): 10
[37]Xu A G.Phys.Rev.E,2005,71(6):066706
[38]Xu A G.Phys.Rev.E,2006,74(1):011505
[39]Yan B,Xu A G,Zhang G C,Ying Y J,Li H.Front.Phys., 2013,8(1):94
[40]Gan Y B,Xu A G,Zhang G C,Li Y J,Li H.Phys.Rev.E, 2011,84(4),046715
[41]Gan Y B,Xu A G,Zhang G C,Zhang P,Li Y J.Europhys. lett.,2012,97(4),44002
[42]Gan Y B,Xu A G,Zhang G C,Li Y J.Phys.Rev.E,2011, 83(5):056704
[43]Gan Y B,Xu A G,Zhang G C,Yang Y.Europhys.lett., 2013,103(2):24003
[44]Chen F,Xu A G,Zhang G C,Li Y J.Phys.Lett.A,2011, 375(21):2129
[45]Chen F,Xu A G,Zhang G C,Li Y J,Succi S.Europhys. lett.,2010,90(5):54003
[46]Meng J P,Zhang Y H,Hadjiconstantinou N G,Radtke G A,Shan X W.J.Fluid Mech.,2013,718:347
[47]Yu H D,Zhao K H.Phys.Rev.E,2001,64(5):056703
[48]Yu H D,Zhao K H.Phys.Rev.E,2000,61(4):3867
[49]Yu H D,Zhao K H.Chin.Phys.Lett.,1999,16(4):271
[50]俞慧丹,赵凯华.物理学报,2000,49(4):L816
[51]俞慧丹,赵凯华.物理学报,1999,48(8):1475
[52]沈智军.中子输运方程数值解与Burgers方程格子Boltzmann方法研究,中国工程物理研究院博士学位论文(导师:沈隆均,袁光伟),北京,2000
[53]Tang G H,Zhang Y H,Gu X J,Emerson D R.Europhys. lett.,2008,83(4):40008
[54]Tang G H,Gu X J,Barber R W,Emerson D R.Phys.Rev. E,2008,78(2):026706
[55]Tang G H,Zhang Y H,Emerson D R.Phys.Rev.E,2008, 77(4):046701
[56]M iller W,Succi S,Mansutti D.Phys.Rev.Lett.,2001, 86(16):3578
[57]Medvedev D,Kassner K.Phys.Rev.E,2005,72(5): 056703
[58]Sun D K,Zhu M F,Pan S Y,Raab D.Acta Mater.,2009, 57(6):1755
[59]Wu W,Zhu M F,Sun D K,Dai T,Han Q Y,Raabe D.IOP Conf.Ser.:Mater.Sci.Eng.,2012,33:012103
[60]Succi S,Vergari P.VLSI Design,1998,6(1-4):137
[61]Chopard B,Droz M,Cellular Automata Modelling of Physical Systems[M],xii ed.,Cambridge University Press, Cambridge,England,1998
[62]Shao X P.Commun.Numer.Meth.En.,2007,23(1):71
[63]Dong Y F,Zhang G C,Xu A G,Gan Y B.Commun.Theor. Phys.,2013,59(1):59
[64]董银峰.固体力学的元胞自动机模型,北京应用物理与计算数学研究所博士后出站报告(合作导师:张广财、许爱国),北京,2012
[65]Jiaung W S,Ho J R.Phys.Rev.E,2008,77(6):066710
[66]Thies M,Lattice Boltzmann modeling w ith free surfaces applied to formation of metal foams,Ph.D thesis,Friedrich-A lexander-Universit?t Erlangen-Nürnberg (FAU),Erlangen,2005
[67]Palpacelli S,Succi S,Spigler R.Phys.Rev.E,2007,76(3):036712
[68]Succi S.Comput.Phys.Commun.,2002,146(3):317
[69]Succi S.Philos.Trans.R.Soc.London,Ser.A,2002, 360(1792):429
[70]Mendoza M,Boghosian B M,Herrmann H J,Succi S. Phys.Rev.D,2010,82(10):105008
[71]Mendoza M,Mu~noz J D.Phys.Rev.E,2010,82(5): 056708
[72]Succi S.J.Phys.A:Math.Theor.,2007,40(26):F559
[73]Melchionna S,Succi S,Hansen J P.Phys.Rev.E,2006, 73(1):017701
[74]Singh S,Subramanian G,Ansumali S.Phys.Rev.E,2013, 88(1):013301
[75]https://dsfd2013.aua.am/speakers/
[76]作为偏微分方程新解法出现的LB模型非常多.例如:李婷婷.弹性动力学变形的格子Boltzmann方法研究,吉林大学博士学位论文(导师:闫广武),长春,2013
[77]闫铂.反应扩散方程的格子Boltzmann方法及数值模拟,吉林大学博士学位论文(导师:闫广武),长春,2013
[78]张建影.用于复Ginzburg-Landau方程的格子Boltzmann方法,吉林大学博士学位论文(导师:闫广武),长春,2011
[79]史秀波.用于波动方程的格子Boltzmann方法及数值模拟研究,吉林大学博士学位论文(导师:闫广武),长春,2010
[80]董银峰.守恒律偏微分方程的格子Boltzmann方法,吉林大学博士学位论文(导师:闫广武),长春,2009
[81]Lai H L,Ma C F.Physica A,2014,395:445
[82]Lai H L,Ma C F.J.Sci.Comput.,2012,53(3):569
[83]Lai H L,Ma C F.Phys.Rev.E,2011,84(4):046708
[84]Lai H L,Ma C F.J.Stat.Mech.-Theory E,2010,P04011
[85]Lai H L,Ma C F.Physica A,2009,388(8):1405
[86]Lai H L,Ma C F.Sci.China Ser.G,2009,52(7):1053
[87]Lai H L,Ma C F.Chin.Phys.Lett.,2008,25(6):2118
[88]赖惠林,马昌凤.中国科学G辑:物理学力学天文学, 2009,39(7):913
[89]http://exa.com/
[90]http://www.openlb.net/
[91]http://www.palabos.org/
[92]Tien C L,Majumdar A,Carey V P,Hijikata K,Inoue T. Microscale Thermophys.Eng.,1997,1(1):71
[93]陈式刚.非平衡统计力学[M],北京:科学出版社,2010
[94]http://www.physics.fudan.edu.cn/tps/people/rbtao/ resume.htm陶瑞宝院士为“International Conference of Discrete Simulation of Fluid Dynamics”国际组织委员会委员:9th(USA,2000);10th(France,2001);11th(China, 2002)Chairman of Local Organizing Comm ittee;12th (Lebnon,2003);13th(USA,2004);14th(Japan,2005)
[95]黄祖洽,丁鄂江.输运理论(第二版)[M],北京:科学出版社,2008
[96]多相复杂系统国家重点实验室与多尺度离散模拟项目组著,基于GPU的多尺度离散模拟并行计算[M],北京:科学出版社,2009
[97]俞慧丹.用格子玻耳兹曼方法模拟复杂流动现象,北京大学博士研究生学位论文(导师:赵凯华),北京,2001
[98]Gunstensen A,Rothman D,Zaleski S,Zanetti G.Phys. Rev.A,1991,43(8):4320
[99]Gunstensen A K,Rothman D H.Europhys.lett.,1992, 18(2):157
[100]Gunstensen A K,Rothman D H.J.Geophys.Res.,1993, 98(B4):6431
[101]Rothman D H,Keller J M.J.Stat.Phys.,1988,52(3-4): 1119
[102]Sw ift M R,Osborn W R,Yeomans J M.Phys.Rev.Lett., 1995,75(5):830
[103]Sw ift M R,Orlandini E,Osborn W R,Yeomans J M.Phys. Rev.E,1996,54(5):5041
[104]Gonnella G,Orlandini E,Yeomans J.Phys.Rev.Lett., 1997,78(9):1695
[105]He X Y,Chen S Y,Zhang R Y.J.Comp.Phys.,1999, 152(2):642
[106]http://www-thphys.physics.ox.ac.uk/people/ JuliaYeomans/
[107]闫铂.燃烧与爆轰问题的LB建模与模拟,北京应用物理与计算数学研究所博士后出站报告(合作导师:许爱国,张广财),北京,2013
[108]Gonnella G,Lamura A,Sofonea V.Phys.Rev.E,2007, 76(3):036703
[109]Xu A G,Zhang G C,Pan X F,Zhang P,Zhu J S.J.Phys. D:Applied Phys.,2009,42(7):075409
[110]Xu A G,Zhang G C,Ying Y J,Zhang P,Zhu J S.Phys. Scr.,2010,81(5):055805
[111]Xu AG,Zhang GC,LiH,Zhu JS.Chin.Phys.Lett.,2010, 27(2):026201
[112]Xu A G,Zhang G C,Li H,Ying YJ,Yu X J,Zhu J S.Sci. China Phys.Mech.,2010,53(8):1466
[113]Xu A G,Zhang G C,Li H,Ying Y J,Zhu J S.Comput. Math.Appl.,2011,61(12):3618
[114]Alexander F J,Chen H,Chen S,Doolen G D.Phys.Rev. A,1992,46(4):1967
[115]Yan G W,Chen Y S,Hu S X.Phys.Rev.E,1999,59(1): 454
[116]Sun C H.Phys.Rev.E,1998,58(6):7283
[117]Sun C H.Phys.Rev.E,2000,61(3):2645
[118]Sun C H,Hsu A T.Phys.Rev.E,2003,68(1):016303
[119]Sun C H,Hsu A T.Comput.Fluids,2004,33(10):1363
[120]Shan X W,Yuan X F,Chen H D.J.Fluid Mech.,2006, 550(1):413
[121]Qu K,Shu C,Chew Y T.Phys.Rev.E,2007,75(3): 036706
[122]Nie X B,Shan X W,Chen H D.Phys.Rev.E,2008,77: 035701(R)
[123]Ran Z.SIAM J.Numer.Anal.,2008,46(1):325
[124]Ran Z.Chin.Phys.Lett.,2007,24(12):3332
[125]Ran Z.Chin.Phys.Lett.,2008,25(11):3867
[126]Ran Z.Chin.Phys.B,2009,18(6):2159
[127]Watari M,Tsutahara M.Phys.Rev.E,2003,67(3):036306
[128]Watari M,Tsutahara M.Phys.Rev.E,2004,70(1):016703
[129]Kataoka T,Tsutahara M.Phys.Rev.E,2004,69(5): 056702
[130]Ansumali S,Karlin I V.J.Stat.Phys.,2002,107(1-2):291
[131]Ansumali S,Karlin I V,¨Ottinger H C.Europhys.lett., 2003,63(6):798
[132]Ran Z,Xu Y P.Chin.Phys.B,2011,20(11):114702
[133]Ran Z,Xu Y P.Int.J.Mod.Phys.C,2009,20(10):1493
[134]Li Y B,Shock R,Zhang R Y,Chen H D.J.Fluid Mech., 2004,519(1):273
[135]Sofonea V,Lamura A,Gonnella G,Cristea A.Phys.Rev. E,2004,70(4):046702
[136]Asinari P.Phys.Rev.E,2006,73(5):056705
[137]Dellar P J.J.Comput.Phys.,2003,190(2):351
[138]Pan X F,Xu A G,Zhang G C,Jiang S.Int.J.Mod.Phys., 2007,18:1747
[139]Gan Y B,Xu A G,Zhang G C,Yu X J,Li Y J.Physica A, 2008,387(8):1721
[140]Chen F,Xu A G,Zhang G C,Gan Y B,Cheng T,Li Y J.Commun.Theor.Phys.,2009,52:681
[141]Chen F,Xu A G,Zhang G C,Li Y J.Commun.Theor. Phys.,2010,54:1121
[142]Chen F,Xu A G,Zhang G C,Li Y J.Commun.Theor. Phys.,2011,56(2):333
[143]Gan Y B,Xu A G,Zhang G C,Li Y J.Commun.Theor. Phys.,56(3):490,2011
[144]Lin C D,Xu A G,Zhang G C,Li Y J,Succi S.Phys.Rev. E,2014,89(1):013307
[145]林传栋,许爱国,张广财,李英骏.凝聚态物理学进展, 2013,2:88
[146]Lin Z F,Fang H P,Tao R B.Phys.Rev.E,1996,54(6): 6323
[147]Fang H P,Wan R Z,Lin Z F.Phys.Rev.E,2002,66(3): 036314
[148]Li H B,Fang H P,Lin Z F,Xu S X,Chen S Y.Phys.Rev. E,2004,69(3):031919
[149]Wang Z W,Fang H P,Lin Z F,Zhou L W.Phys.Rev.E, 2000,61(6):6837
[150]Fang H P,Wang Z W,Lin Z F,Liu M R.Phys.Rev.E, 2002,65(5):051925
[151]Li H B,Lu X Y,Fang H P,Qian Y H.Phys.Rev.E,2004, 70(2):026701
[152]Wen B H,Li H B,Zhang C Y,Fang H P.Phys.Rev.E, 2012,85(1):016704
[153]Wan R Z,Fang H P,Lin Z F,Chen S Y.Phys.Rev.E,2003, 68(1):011401
[154]Fan L W,Fang H P,Lin Z F.Phys.Rev.E,2001,63(5): 051603
[155]Lin Z F,Fang H P,Xu J J,Zi J.Phys.Rev.E,2003,67(2): 025701(R)
[156]曹亮.非平衡系统的涨落理论与自由能关系,北京师范大学博士学位论文,(导师:郑志刚,M ichael Cross),北京,2012
[157]Ji Y P,Kang X Y,Liu D H.Chin.Phys.Lett.,2010,27(9): p094701
[158]Ji Y P,Kang X Y,Liu D H.Chin.Phys.Lett.,2009,26(7): 074702
[159]Kang X Y,Ji Y P,Liu D H,Jin Y J.Chin.Phys.B,2008, 17:1041
[160]Kang X Y,Liu D H,Zhou J,Jing Y J.Chin.Phys.Lett., 2005,22(11):2873
[161]Kang X Y,Liu D H,Zhou J,Jing Y J.Chin.Phys.Lett., 2005,22(6):1456
[162]Xu Y Q,Tian F B,Li H J,Deng Y L.Theor.Appl.Mech. Lett.,2012,2(2):,024001
[163]Xu Y Q,Tian F B,Deng Y L.Int.J.Bioma.,2013,6(1): 1250061
[164]Tian FB,BhartiRP,Xu YQ.Comput.Mech.,2014,53(2): 257
[165]Xu Y Q,Tang X Y,Tian F B,Peng Y H,Xu Y,Zeng Y J. Comput.Method Biomec.,2014,17(9):978
[166]Deng H B,Xu Y Q,Chen D D,Dai H,Wu J,Tian F B. Comput.Mech.,2013,52(6):1221
[167]Wei Q,Xu Y Q,Tian F B,Gao T X,Tang X Y,Zu W H. Bio-Med.Mater.Eng.,2014,23:S495
[168]Wang M R,Kang Q J.J.Comput.Phys.,2010,229(3):728
[169]Wang M R,Wang J K,Chen S Y.J.Comput.Phys.,2007, 226(1):836
[170]Wang J K,Wang M R,Li Z X.Comm.Nonlinear Sci.Numer.Simulat.,2008,13(3):575
[171]Wang J K,Wang M R,Li Z X.Inter.J.Thermal Sci.,2007, 46(3):228
[172]Wang J K,Wang M R,Li Z X.J.Colloid Interface Sci., 2006,296(2):729
[173]Chen S G,Sun Q C,Jin F,Liu J G.Sci.China-Phys.Mech. Astron,2013,DOI:10.1007/s11433-013-5178-2.
[174]http://sw rh.whu.edu.cn/FacultyLists/Hydroelectric/2013 /1009/1934.htm l
[175]Cheng Y G,Zhang H.Comput.Fluids,2010,39(5):871
[176]Grunau D W,Lookman T,Chen S Y,Lapedes A S.Phys. Rev.Lett.,1993,71(25):4198
[177]Kang Q J,Zhang D X,Chen S Y,He X Y.Phys.Rev.E, 2002,65(3):036318
[178]李莎.基于格子Boltzmann方法的多孔介质孔隙特性的研究,中科院过程工程研究所硕士论文(导师:雍玉梅,杨超),北京2012
[179]张婷.多孔介质内多组分非均匀相反应流的格子Boltzmann方法研究,华中科技大学博士学位论文(导师:施保昌,郭照立),武汉,2012
[180]张云.多孔介质中流动的格子Boltzmann方法研究,中国石油大学博士学位论文(导师:杨朝合,葛蔚),北京, 2011
[181]柴振华.基于格子Boltzmann方法的非线性渗流研究,华中科技大学博士学位论文(导师:施保昌,郭照立),武汉,2009
[182]鲁建华.基于格子Boltzmann方法的多孔介质内流动与传热的微观模拟,华中科技大学博士学位论文(导师:施保昌,郭照立),武汉,2009
[183]许友生,李华兵,方海平,黄国翔.物理学报,53,773, 2004
[184]严微微,刘阳,许友生.西安石油大学学报(自然科学版),22,149,2007
[185]Sukop M C,Huang H,Lin C L,Deo M D,Oh K.Phys. Rev.E,2008,77(2):026710
[186]Huang H,Wang L,Lu X.Comput.Math.Appl.,2011, 61(12):3606
[187]Chen R,Shao J G,Zheng Y Q,Yu H D,Xu Y S.Commun. Theor.Phys.,2013,59(3):370
[188]Ladd A J C.J.Fluid Mech.,1994,271:285
[189]Ladd A J C.J.Fluid Mech.,1994,271:311
[190]Sun D K,Jiang D,Xiang N,Chen K,Ni Z H.Chin.Phys. Lett.,2013,30(7):074702
[191]Sun D K,Xiang N,Jiang D,Chen K,Yi H and Ni Z H. Chin.Phys.B,2013,22(11):114704
[192]Sun D K,Wang Y,Jiang D,Xiang N,Chen K,Ni Z H. Appl.Phys.Lett.,2013,103(7):071905
[193]Rakotomalala N,Salin D,Watzky P.Phys.Fluids,1996,8: 3200
[194]Chen X,Zhong C,Yuan X.Comput.Math.Appl.,2011, 2011,61:3577
[195]Chen X.Commun.Comput.Phys.,2010,7:212
[196]Boek E S,Chin J,Coveney P V.Int.J.Mod.Phys.B,2003, 17(01n02):99
[197]Succi S,Vergassola M,Benzi R.Phys.Rev.A,1991,43: 4521
[198]CercignaniC.IllnerRand PulvirentiM.TheMathematical Theory of Dilute Gases(Applied Mathematical Sciences vol 106)[M],New York:Springer,1994
[199]Bhatnagar P L,Gross E P,Krook M.Phys.Rev.,1954, 94(3):511
[200]Chen F,Xu A G,Zhang G C,Li Y J.Commun.Theor. Phys.,2011,55(2):325
[201]Chen F,Xu A G,Zhang G C,Wang Y L.Front.Phys., 2014,9(2):246
[202]Mezrhab A,Moussaoui M A,Jam i M,Naji H,Bouzidi M.Phys.Lett.A,2010,374(34):3499
[203]Zheng L,Shi B C,Guo Z L.Phys.Rev.E,2008,78(2): 026705
[204]Chen F,Xu A G,Zhang G C,Li Y J.Theroe.Appl.Mech. Lett.,2011,1:052004
[205]Fickett W,Davis W,Detonation:theory and experiment, Dover Publications,Inc.M ineola,New York,1979
[206]孙锦山,朱建士.理论爆轰物理[M],北京:国防工业出版社,1995
[207]孙承纬,卫玉章,周之奎.应用爆轰物理[M],北京:国防工业出版社,2000
[208]Wang C,Zhang X X,Shu CW,Ning JG.J.Comput.Phys., 2012,231(2):653
[209]Tan S R,Wang C,Shu C W,Ning J G.J.Comput.Phys., 2012,231(6):2510
[210]Succi S,Bella G,Papetti F.J.Sci.Comput.,1997,12(4): 395
[211]FilippovaO,Hanel D.J.Comput.Phys.,2000,158(2):139
[212]Filippova O,Haenel D.Comput.Phys.Comm.,2000, 129(1):267
[213]Yamamoto K,He X Y,Doolen G D.J.Stat.Phys.,2002, 107(1-2):367
[214]Yamamoto K,Takada N,M isawa M.P.Combust.Inst., 2005,30(1):1509
[215]Lee T,Lin C L,Chen L D.J.Comput.Phys.,2006,215(1): 133
[216]Lee E L,Tarver C M.Phys.Fluids,1980,23:2362
[217]Lin C D,Xu A G,Zhang G C,Li Y J.e-print arXiv: 1308.0653
[218]Zhang R Y,He X Y,Doolen G,Chen S Y.Adv.Water Resour.,2001,24(3):461
[219]Gunstensen A K,Rothman D H.Physica D,1991,47(1-2): 53
[220]Nie X B,Qian Y H,Doolen G D,Chen S Y.Phys.Rev.E, 1998,58:6861
[221]He X Y,Zhang R Y,Chen S Y,Doolen G D.Phys.Fluid., 1999,11:1143
[222]Zhang R Y,He X Y,He X Y.Commun.Comput.Phys., 2000,129(1-3):121
[223]Clark T T.Phys.Fluid,2003,15:2413
[224]Lee T,Lin C L.J.Comput.Phys.,2005,206(1):16
[225]Lee T,Fischer P.Phys.Rev.E,2006,74(4):046709
[226]Lee T,Fischer P.Phys.Rev.E,2006,74(4):046709
[227]Lee T,Liu L.Phys.Rev.E,2008,78(1):017702
[228]Chiappini D,Bella G,Succi S,Toschi F,Ubertini S.Commun.Comput.Phys.,2010,7(3):423
[229]Li Q,Luo K H,Gao Y J,He Y L.Phys.Rev.E,2012, 85(2):026704
[230]Zu Y Q,He S.Phys.Rev.E,2013,87(4):043301
[231]Liu G J,Guo Z L.Int.J.Numer.Method H.,2013,23(1): 176
[232]Sbragaglia M,Benzi R,Biferale L,Chen H,Shan X,Succi S.J.Fluid Mech.,2009,628:299
[233]Scagliarini A,Biferale L,Sbragaglia M,Sugiyama K, Toschi F.Phys.Fluid,2010,22(5):055101
[234]Biferale L,Mantovani F,Sbragaglia M,Scagliarini A, Toschi F,Tripiccione R.Phys.Fluid,2010,22(11): 115112
[235]Scagliarini A,Biferale L,Sbragaglia M,Sugiyama K, Toschi F.Phys.Scripta,2010,T142:014017
[236]Biferale L,Mantovani F,Pozzati F,Sbragaglia M, Scagliarini A,Schifano F,Toschi F,Tripiccione R.Phil. Trans.R.Soc.A,2011,369:2448
[237]Biferale L,Mantovani F,Sbragaglia M,Scagliarini A, Toschi F,Tripiccione R.Europhys.Lett.,2011,94(5): 54004
[238]Biferale L,Mantovani F,Sbragaglia M,Scagliarini A, Toschi F,Tripiccione R.Phys.Rev.E,2011,84(1):016305
[239]许爱国,张广财.非平衡与多相复杂系统模拟研究:Lattice Boltzmann理论与应用,中科院理论物理研究所专题学术报告,2013年10月25日. http://www.itp.cas.cn/xshd/ztxxbg/201310/t20131024 3961895.htm l
Nonequilibrium and multiphase com p lex system s are ubiquitous in natural and engineering fi elds. The Lattice Boltzm ann(LB)m ethod/m odel is originated from the lattice gas or autom ata m odel which was p roposed to investigate com p lex behaviors in various com p lex system s.The current Lattice Boltzm ann K inetic M odel(LBKM)is rooted in the fundam ental equation of the nonequilibrium statistical physics,the Boltzmann equation.The LB model is reviewed from a physical point of view.A uni fi ed theory for the single relation tim e and mu ltip le relaxation tim e LBKM s is presented.The m odeling and simu lations of various nonequilibrium and multiphase com p lex system s are introduced.Firstly,we brie fl y review the progress in m odeling multiphase fl ow s,compressible fl ow s,soild m aterial kinetics,etc.Then,we give m ore space to the p rogress in studying hydrodynam ic interfacial instabilities,combustion phenomena,etc.It is stressed that,via the LBKM,one can probe the nonequilibrium behavior through analyzing the high-order m om ents which are macroscopic quantities.The LBKM can be used to investigate the macroscopic behaviors of the system due to its deviations from the therm odynam ic equilibrium,which is beyond the traditional m odeling based on continuum assum p tion.Besides the deeper physical insights into the kinetic procedures,such a methodology and observations are indicative for im proving the physical m odels from a m acroscopic level.
M odeling and Sim ulation of Nonequilibrium and M ultiphase Com p lex System s—Lattice Boltzm ann K inetic Theory and App lication
Xu Ai-Guo1,2,3*,Zhang Guang-Cai1,3,Li Ying-Jun4,Li Hua1,2
1.National Key Laboratory of Computational Physics,Institute of Applied Physcis and Computational Mathematics, P.O.Box 80009-26,Beijing 100088 2.Center for Applied Physics and Technology,MOE Key Center for High Energy Density Physics Simulations, College of Engineering,Peking University,Beijing 100871,P.R.China 3.State Key Laboratory of Theoretical Physics,Institute of Theoretical Physics, Chinese Academ y of Sciences,Beijing 100190,China 4.State Key Laboratory for GeoMechanics and Deep Underground Engineering, China University of M ining and Technology,Beijing 100083
lattice Boltzm ann;kinetic m odel;non-equilibrium e ff ects;com p lex system s
O41
A
Received date:2013-12-5
*Xu Aiguo@iapcm.ac.cn
1000-0542(2014)03-0136-32 136
