湖泊水动力模型外部输入条件不确定性和敏感性分析

李一平,邱 利,唐春燕,布旻晟,田 威,余钟波,Kumud Acharya(1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京 210098；2.河海大学环境学院,江苏 南京 210098；.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098；.河海大学机电工程学院,江苏 南京 210098；.江苏省水文水资源勘测局,江苏 南京 210029)

湖泊水动力模型外部输入条件不确定性和敏感性分析

李一平1,2,3*,邱 利1,2,唐春燕1,2,布旻晟4,田 威5,余钟波3,Kumud Acharya3(1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京 210098；2.河海大学环境学院,江苏 南京 210098；3.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098；4.河海大学机电工程学院,江苏 南京 210098；5.江苏省水文水资源勘测局,江苏 南京 210029)

以我国典型的大型浅水湖泊太湖为研究区域,采用国内外常用的环境流体动力学模型(EFDC),结合拉丁超立方取样(LHS)方法,研究湖泊水动力模型中4个重要的外部输入条件,即3个边界输入条件(出入湖流量、风速、风向)和1个初始输入条件(初始水位),对模型水动力模拟结果(水位、水龄以及流场)的影响与贡献.结果表明,初始水位的设定对模拟全湖水位和水龄产生决定性影响,不确定性的贡献率分别达到85.73%和66.125%,对垂向平均流速影响的贡献率只有3%;风速对表面流速模拟结果影响较大,贡献率达到58.70%,而对水位和水龄的贡献率分别为 5.25%和 3.00%.在垂向上,各层流速受外部输入条件不确定性的影响规律相似,贡献率排序为风速(55%～60%)>风向(10%～15%)>初始水位≈出入湖流量(1%～5%).因此在模拟大型浅水湖泊水动力过程时,可以根据不同的输出目标能够有针对性地提高外部输入条件的准确度,为提高模型精确度提供有效信息.

输入条件；不确定性分析；敏感性分析；environmental fluid dynamic code (EFDC)；大型浅水湖泊

随着计算、监测和通讯技术的进步,河湖水环境模拟预测技术也不断提高,目前模拟河湖水动力过程的模型有很多,比如QUAL2K(River and Stream Water Quality Model)、MIKE11、WASP (Water Quality Analysis Simulation Program)和EFDC(Environmental Fluid Dynamic Code)[1].为了使水动力模型预测的结果能够更好地服务于水环境预测及管理,提高模型输出结果的准确度显得十分重要.然而很多因素会影响模型结果的准确度,总的来说不确定性来源于三大方面:参数估计、外部输入条件以及模型结构[2].外部输入条件包括边界输入条件和初始输入条件,然而监测技术、监测设备以及操作人员水平等的局限性导致外部输入条件值本身存在不确定性[3],而且在不同文献中的取值也存在差别. Ahsan等[3]研究表明Mississippi海峡的水动力模型对水深和淡水入流量十分敏感,Mississippi海峡的浅水区域对水深条件十分敏感,水深对该浅水区域温度和盐度输出结果的不确定性贡献率达到 88%.大型浅水湖泊(以太湖为例)因为“面大、水浅”的特性和周边河网的密集性,其水动力过程复杂多变,增加了水动力过程的模拟难度,因此研究外部输入条件对大型浅水湖泊水动力模拟结果的不确定性和敏感性影响具有重要的意义[4-6].目前用于不确定性分析方法很多,如敏感性分析、一阶误差分析、蒙特卡罗方法、Bootstrap 方法、最大似然方法、贝叶斯法、离散Bayes 法、区域敏感性分析方法、神经网络法、遗传算法、模糊数学法、傅立叶敏感性检验法等. 国内外学者在这方面做了很多研究工作,其中敏感性分析、FOEA、蒙特卡罗方法和Bootstrap方法是不确定性分析最常用的方法[7].而拉丁超立方抽样法(Latin hypercube sampling, LHS)是一种分层的蒙特卡罗(Monte Carlo)抽样技术,与 Monte Carlo随机抽样法相比,LHS的样本能够更加精确地反映外部输入条件的概率函数分布,能够利用最少的样本数反映外部输入条件最大的信息量[8]. LHS最早由McKay提出,由Stein给出比较数学化的表述.LHS是一种可以替代Monte Carlo方法的效果好的方差缩减技术,在仿真模拟、优化计算和可靠性计算方面得到较为广泛的应用[9].本研究以我国典型的大型浅水湖泊太湖为例,选取湖泊水动力模型中4个重要的外部输入条件,即3个边界输入条件(出入湖流量、风速、风向)和1个初始输入条件(初始水位),利用LHS方法对外部输入条件取值随机取样并进行不确定分析,并且利用标准秩逐步回归法对外部输入条件进行敏感性分析,量化每个外部输入条件对模拟结果不确定性的贡献率.以期通过定量分析每个外部输入数据对模型结果不确定性的贡献率,找出对模型结果不确定性影响较大的外部输入条件,从而为有效地提高模型模拟精度提供可靠的信息.

1 研究区域

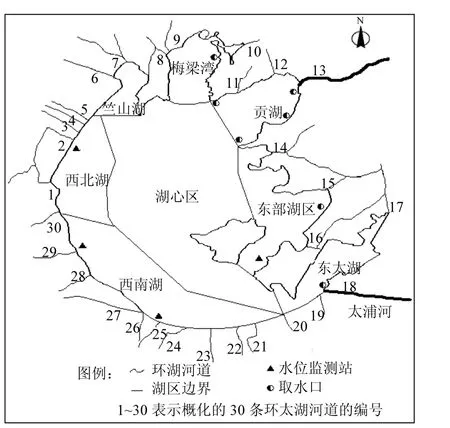
图1 研究区域Fig.1 Study area

太湖(119°08′E～122°55′E,30°05′N～32°08′)是我国第三大浅水湖泊,湖泊总面积 2338km2.太湖平均水深 1.9m,最大水深为 2.6m,太湖底部呈现坡度为0°0′19.66′的平底地形,水深小于1.5m的浅水区域主要位于东部湖区,占总表面积的19.3%.水深最大(>2.5m)的区域主要位于西北湖区,占总表面积的 8.4%.太湖周边水系复杂,本研究将环湖河道概化为30条河,编号如图1所示.太湖流域夏季主导风向是东南风,冬季主导风向是西北风,平均风速 3.5～5.0m/s[10-11].根据太湖各个湖区的特点,本研究将太湖划分为 8个子区域(图1),竺山湖、梅梁湾、贡湖、西北湖区、西南湖区、湖心区、东部湖区和东太湖湾[12].

2 研究方法

2.1 模型建立

EFDC(Environmental Fluid Dynamic Code)是国内外常用的环境流体动力学模型,本研究采用EFDC模型来模拟太湖的水动力过程.模型采用笛卡尔直角坐标网格,共划分 4464个网格,每个网格单元边长为 750m.为了较好地模拟湖底地形,垂直方向采用σ坐标,平均分为3层.根据流体静力学连续性和避免产生 σ坐标带来的压力梯度错误,应使湖底坡度小于0.33[12].模型计算时间步长为10s,模拟时间为365d.

2.2 不确定性结果统计分析方法

在 LHS方法计算结果统计中,外部输入条件个数记为 k,抽样组数记为 n,每一个外部输入条件X1、X2,…,Xk在各自的取值范围内等分成N组,每组随机抽取一个值,n个k维变量组值共产生n个预测值,然后将n个预测值按大小排列,并分配给最小的预测值的累积概率为 1/n,分配给次最小的预测值的累积概率为 2/n,依此类推得预测值的经验分布函数,此经验分布函数提供了子样的分位值,即第m个预测值是m/n×100%的子样分位值[13-14].其中5%、95%百分位值代表了由边界条件引起的不确定性的边界,5%代表下边界, 95%代表上边界[15].

2.3 敏感性分析方法

敏感性分析采用标准秩逐步回归法,该方法将原有数据转化为相关秩系数,再进行标准化回归分析,解决了输入和输出之间的非线性关系,得到标准回归系数(SRRC)和决定系数(R2).SRRC2用来表示每个外部输入条件对整个输出结果方差的贡献率,其值越大则表明该输入条件越敏感,对模型结果不确定性的贡献率也越大.R2是表示回归模型分析的可行性程度,其值越大回归分析越可行,一般R2值大于0.7,即可认为回归分析合理[16].

2.4 外部输入条件的统计特征及LHS抽样方法

本研究选取出3个边界条件(出入湖流量、风速、风向)和1个初始条件(初始水位)作为外部输入条件.表 1给出了各外部输入条件取值的最大值和最小值,假设各外部输入条件之间是相互独立的,且在取值范围内服从均匀分布.环湖河道概化为30条河,其值以2005年实测数据为基础,模拟抽样在流量 90%～110%范围内进行.太湖夏季主导风向为东南风,本研究采用东风到南风(包括东南风)之间的风向作为风向取值范围.

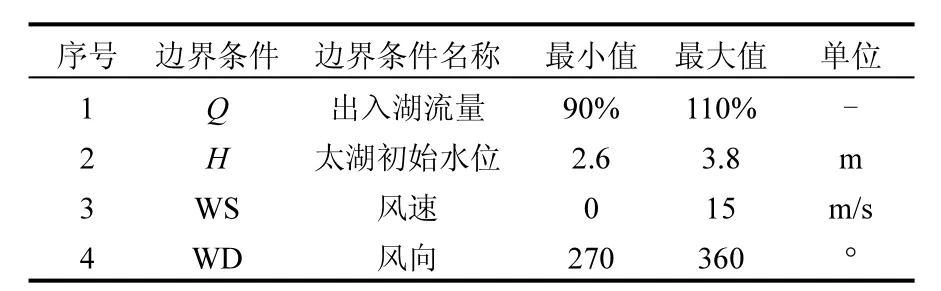
表1 LHS抽样分析模型外部输入条件的范围Table 1 Ranges of boundary and initial conditions used for the Latin Hypercube Sampling

本研究采用 LHS抽样方法随机抽样生成200组外部输入条件[14-15],每组外部输入条件数据都用EFDC模型运行一次,最后得到200组特定目标的输出结果,利用这200组结果定量分析4个外部输入条件对模型模拟结果的不确定性影响.考虑到太湖是典型的风生流,湖流垂向可能存在切变[17].因此本研究选取水位、水龄和垂向3层流速(表层、中层和底层)作为模型特定的模拟目标.最后利用 surfer 软件分析外部输入条件对整个湖区不同模拟目标的不确定性影响[17].

3 结果与讨论

3.1 外部输入条件不确定性分析

本研究利用EFDC运行第365d的水位、水龄和垂向 3层流速作为输出目标,通过分析 200组模型输出结果,定量分析各外部输入条件对模拟目标的影响,并进行不确定性分析.外部输入条件不确定性以模拟目标值的均值、5%、95%分位值以及方差来进行量化描述.

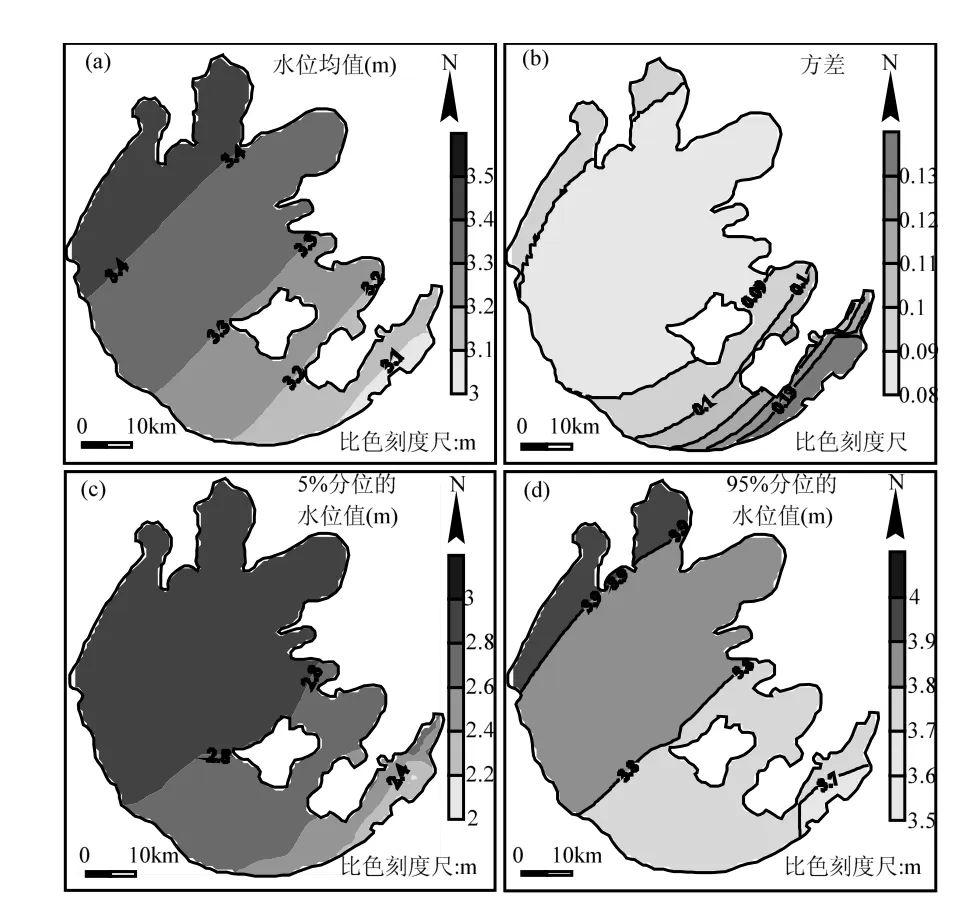
图2 模拟水位的均值, 5%分位值, 95%分位值和方差的空间分布Fig.2 Mean, 5%, 95% and variance of the simulated water level

3.1.1 以水位为输出目标 200组 4个外部输入条件的 LHS抽样组合的水位模拟结果的均值、5%和 95%百分位值如图 2所示,结果表明±10%的出入湖流量变化以及初始水位、风速和风向在一定范围内的变化会造成模拟水位的分异性.均值、5%和95%的水位值都呈现出明显的空间分异性,几个典型湖区的水位分别如下:西北湖区分别为 3.4,2.8,3.9m,湖心区分别为 3.3,2.7, 3.8m,东太湖分别为 3.1,2.2,3.7m.不同频率下的水位大致呈现出由东南至西北方向逐渐雍高的趋势,其水位变化梯度也不相同, 95%水位空间分布变化梯度最大,水位均值空间变化梯度次之,5%水位空间变化梯度最小.图2(b)给出了200组模拟水位方差的空间分布,量化了 4个外部输入条件对水位结果的不确定性影响.方差值越大表明外部输入条件对水位计算结果产生的不确定性也越大.湖心区和贡湖湾的水位方差相对较小约为 0.08,沿着东南和西北方向水位方差分别逐渐增加,特别是东南方向,方差变化范围为[0.08,0.18].整个太湖水位都受到4个外部输入条件不确定性的影响,特别是东太湖水位受不确定性的影响最大,原因可能是在风的作用下,太湖东南部水位最低,可推测湖泊水位较低的区域受外部输入条件的不确定性影响较大.综上所述,当以水位为输出目标时:整个湖区的水位都受到了 4个外部输入条件的不确定性影响;东太湖受不确定性影响明显大于湖心区和其他湖区.

3.1.2 以水龄为输出目标 200组4个外部输入条件的 LHS抽样组合对输出水龄值产生的不确定性结果如图 3所示,结果同样表明外部输入条件对水龄产生了不确定性影响.模拟水龄的均值、5%分位和 95%分位的水龄值都呈现出明显的空间分异性,几个典型湖区的水龄分别如下:竺山湾分别为70,50,100d,西南湖区分别为180,150,200d,东太湖分别为190,200,240d.竺山湾和西北湖区的模拟水龄值最小,沿着西南方向水龄逐渐增加,在东太湖区域模拟水龄值最大.对于同一湖区,不同频率下的水龄表现出的规律是:95%分位的水龄值>平均水龄值>5%分位的水龄值.200组抽样组合的水龄模拟结果方差空间分布[图 3(b)]量化了不确定性影响.竺山湾和西北湖区的水龄方差最大约为800,而其他湖区的水龄方差相对较小约为300,整个太湖的水龄模拟结果方差变化范围为[100,900],远大于水位模拟结果的方差变化范围.这表明水龄受外部输入条件的不确定性影响很大,尤其是竺山湾和西北湖区受不确定性的影响最大.原因可能是太湖入湖河流主要集中在竺山湾和西北湖区附近,该区域水动力扰动最强,水体交换速率较快,因此可以推测在湖泊入湖河道附近水动力扰动较强的区域,水龄受外部输入条件不确定性的影响较大.综上所述,当以水龄为输出目标时:外部输入条件对水龄产生的不确定性影响很显著(远远大于水位);竺山湾和西北湖区受外部输入条件的不确定性影响明显大于其他湖区. 3.1.3 以流速为输出目标 200组4个外部输入条件的LHS抽样组合对表层流速产生的不确定性结果如图4所示.模拟表层流速的均值、5%分位和95%分位的水龄值都呈现出明显的空间分异性,在近岸湖区分别为 3,1,5m/s,在远离湖岸区域分别为2,0.5,3m/s,在湖心区分别为1,0.3, 2m/s.表层流速在沿岸湖区相对较大,由湖岸到湖心方向流速逐渐减小,并且不同分位下表层流速的空间变化梯度也不相同,5%分位的流速值<均值<95%分位的流速值,这表明外部输入条件的变化对表层流速模拟结果产生较大的不确定性.200组抽样组合的表层流速模拟结果方差的空间分布如图 4(b)所示,沿岸区域的表层流速方差最大约为10,而其他区域的方差相对较小,不确定性方差范围[0,15].表明沿岸区域表层流速受到外部输入条件的不确定性影响较大,而湖心区受到的不确定性的影响较小.

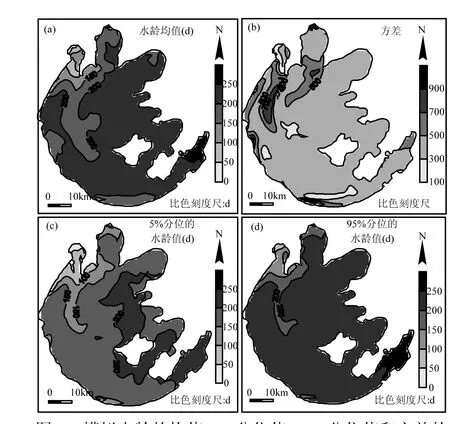
图3 模拟水龄的均值, 5%分位值, 95%分位值和方差的空间分布Fig.3 Mean, 5%, 95% and variance of the simulated water age

表层流速、水位和水龄的不确定性空间分布形式各不相同,外部输入条件对水龄产生的不确定性远大于对表层流速和水位产生的不确定性,而对表层流速的不确定性大于对水位产生的不确定性.表明针对不同的模拟目标,边界条件所产生的不确定性空间分布和影响程度也不同.当以表层流速为输出目标时:表层流速受到外部输入条件的不确定性影响介于以水位与水龄为输出目标时的影响之间;沿岸区域的表层流速受到外部输入条件的不确定性影响最大.

图4 模拟表层流速的均值, 5%分位值, 95%分位值和方差的空间分布Fig.4 Mean, 5%, 95% and variance of the simulated flow velocity in the surface layer

3.2 边界条件敏感性分析

3.2.1 以水位为输出目标 对 200组外部输入条件组合和输出目标水位值进行逐步秩回归分析,得出决定系数R2为0.92(表2),表明该回归分析是可行的.太湖初始水位 SRRC2值最大(85.73%),表明太湖初始水位对水位模拟结果最敏感,不确定性贡献率占绝对主要的地位.其次是风速的SRRC2值(5.25%),表明相对于其他3个边界条件,风速对水位的模拟结果比较敏感.出入湖流量和风向的SRRC2值均小于1%,表明这两个边界条件对水位模拟结果不确定性的贡献率较小,敏感性较差.4个外部输入条件对模拟水位结果不确定性的贡献率排序为:太湖初始水位(85.73%)>风速(5.25%)>风向(0.86%)>出入湖流量(0.10%).综上所述,以太湖水位为模拟目标时,初始水位对模拟结果的不确定性贡献率最显著,是最敏感的外部输入条件,而风速、风向和出入湖流量对水位敏感性较差.

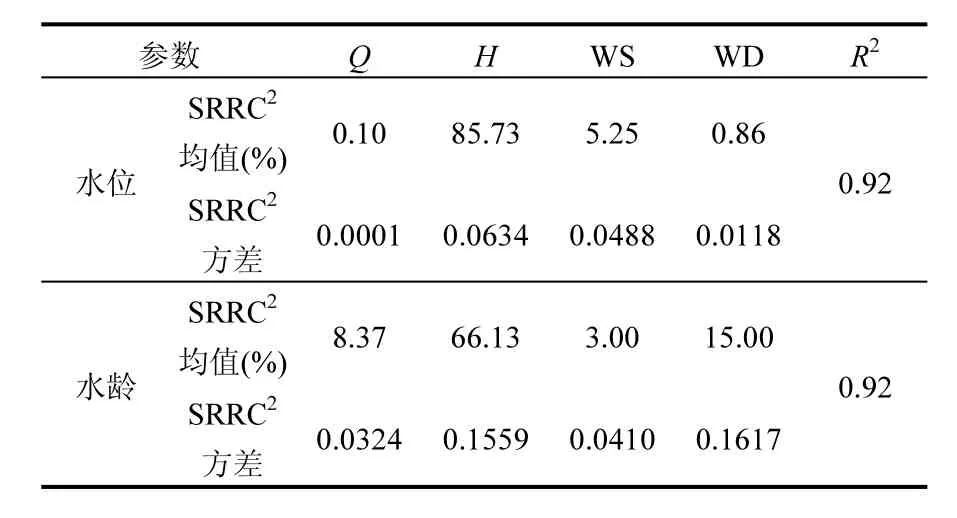
表2 4个外部输入条件对水位和水龄不确定性的SRRC2均值和标准方差Table 2 Mean and standard deviation of SRRC2values of four input conditions on the uncertainty of the simulated water level and water age

3.2.2 以水龄为输出目标 对200组外部输入条件组合和输出目标水龄值进行逐步秩回归分析,得出决定系数R2为0.92(表2),表明该回归分析是可行的.太湖初始水位的 SRRC2值最大为66.125%,表明初始水位对水龄模拟结果最敏感,不确定性的贡献显著.风向和出入湖流量的SRRC2值分别为15.00%和8.37%,表明3个边界条件中风向对水龄模拟结果比较敏感,其次是出入湖流量,而风速的 SRRC2值只有 3.00%,表明风速对水龄模拟结果不确定性的贡献较小,敏感性较差.4个外部输入条件对模拟水龄结果不确定性的贡献率排序为:太湖初始水位(66.125%)>风 向 (15.00%)>出 入 湖 流 量(8.37%%)>风速(3.00%).综上所述,以水龄为模拟目标时,初始水位对结果不确定性的贡献率最显著,是最敏感的外部输入条件,其次为风向和出入湖流量,而风速对模拟结果的贡献率较小,即敏感性较差.

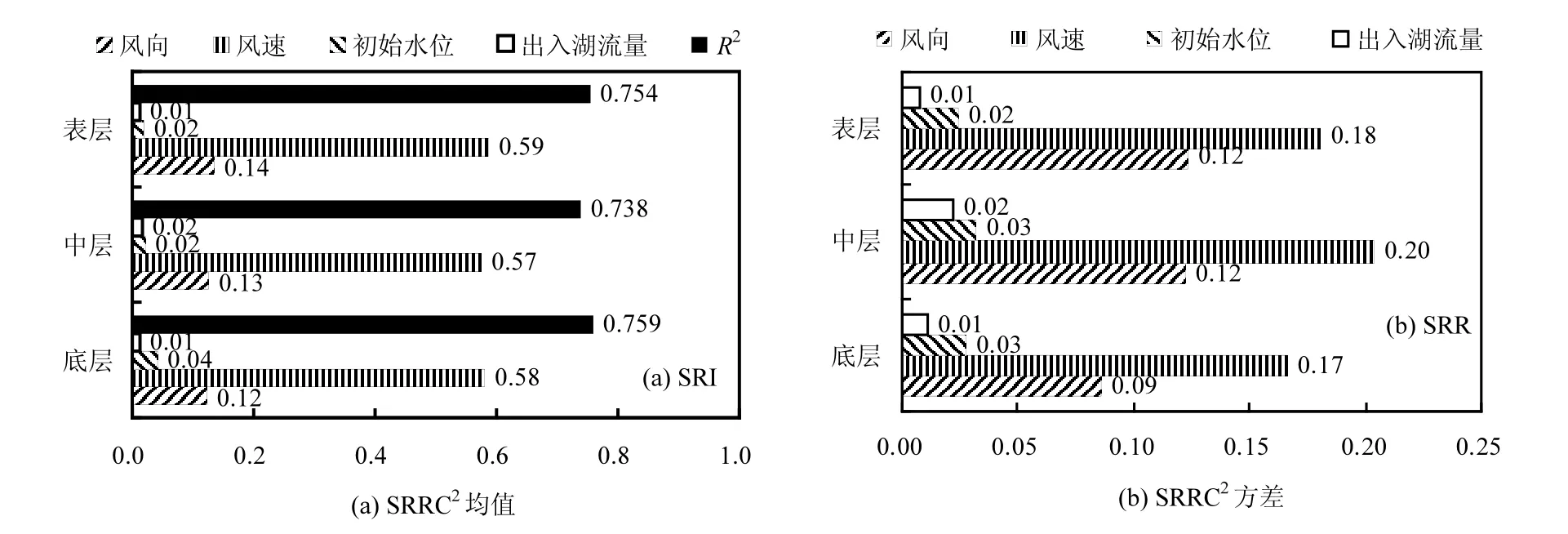
图5 4个外部输入条件对各层流速的不确定性的SRRC2均值和标准方差Fig.5 Mean and stand deviation of SRRC2of four input conditions on the uncertainty of the simulated flow velocity in different layers

3.2.3 以流速为输出目标 对 200组外部输入条件组合及输出目标表层流速进行逐步秩回归分析,决定系数R2为0.754,表明逐步回归分析是可行的(图 5).风速贡献率为 58.70%,表明风速对表层流速模拟结果很敏感,风速的不确定性影响显著.其次风向的SRRC2值为13.52%,表明风向也是对表层流速变化较敏感的一个边界条件.风速和风向对太湖表层流速不确定性的贡献率占绝对主导地位.而出入湖流量和初始水位对太湖表层流速的不确定性贡献率均小于 2%,表明其敏感性较差.4个外部输入条件对表层流速不确定性的贡献率排序为:风速(58.70%)>风向(13.52%)>太湖初始水位(1.93%)≈出入湖流量(1.27%).综上所述:以表层流速为输出目标时,风速对模拟结果不确定性的贡献率最显著,是最敏感的边界条件,其次是风向,而初始水位和出入湖流量的敏感性均较差.

4个外部输入条件对垂向各层流速模拟结果的不确定性贡献率的平均值和标准方差如图5所示,各层的决定系数R2均大于0.7,表明外部输入条件与各层流速之间的回归分析是可行的.从图中可知,风速对各层流速不确定性的贡献率都最大,均在55%～60%之间.其次是风向,不确定性贡献率均在 10%～15%之间.而初始水位和出入湖流量对各层流速不确定性的贡献率都较小,均在 1%～5%之间.表明外部输入条件对各层流速的不确定性影响规律相似,贡献率排序均为风速(55%～60%)>风向(10%～15%)>初始水位≈出入湖流量(1%～5%).由图5可知,外部输入条件对流速不确定性的贡献率在垂向上差距很小.原因可能是太湖属于典型的浅水湖泊,其特点是风生流,由于水浅的特性使得风场对流速的影响在垂向上差别很小.由图5(b)可知风速和风向对每层流速不确定性贡献率的方差很大,表明这两个边界条件对各层流速的不确定性影响在空间上的变化较大.

综上所述:对于大型浅水湖泊,外部输入条件对各层流速的不确定性影响规律相似,风速对各层流速不确定性的贡献率最显著,是最敏感的外部输入条件,其次是风向,而初始水位和出入湖流量的敏感性较差.并且风速和风向对流速不确定性的贡献率空间差异性很大.

4 结论

4.1 对于大型浅水湖泊的水动力模拟过程,外部输入条件的不确定性对模拟结果(以水位、水龄以及流速表征)产生影响.对于不同的输出目标,水龄受外部输入条件的不确定性影响最大,其次是垂向平均流速,水位受到的不确定性影响最小.以水位为输出目标时,湖泊水位较低区域受外部输入条件的不确定性影响较大;以水龄为输出目标时,在湖泊入湖河道附近水动力扰动较强的区域受到的不确定性最大;而以流速为输出目标时,湖泊沿岸区域受到的不确定性影响最大,且不确定性影响在垂向上差别很小.

4.2 针对不同的输出目标,4个重要外部输入条件对模拟结果产生的不确定性贡献率也不相同.初始水位对全湖的水位和水龄模拟结果产生决定性影响,贡献率分别达到85.73%和66.125%,而对垂向平均流速不确定性影响的贡献率只有3%;风速对垂向平均流速模拟结果产生决定性影响,贡献率达到 55%～60%,而对水位和水龄的不确定性贡献率分别只有5.25%和3.00%.

[1] Zhao X, Shen Z Y, Xiong M, et al. Key uncertainty sources analysis of

water quality model using the first order error method [J]. International

Journal of Environmental Science and Technology, 2011,8(1):137-148. [2] Lindenschmidt K E, Fleischbein K, Baborowski M. Structural uncertainty in a river water quality modelling system [J]. Ecological Modelling, 2007,204(3/4):289-300.

[3] Blumberg A F, Georgas N. Quantifying uncertainty in estuarine and coastal ocean circulation modeling [J]. Journal of Hydraulic Engineering, 2008,134(4):403-415.

[4] 秦伯强.太湖生态与环境若干问题的研究进展及其展望 [J].湖泊科学, 2009,21(4):445-455.

[5] 王 鹏,王胜艳,郝少盼,等.模拟扰动条件下太湖沉积物的再悬浮特征 [J]. 水科学进展, 2010,21(3):309-404.

[6] 丁艳青,朱广伟,秦伯强,等.波浪扰动对太湖底泥磷释放影响模拟 [J]. 水科学进展, 2011,22(2):273-278.

[7] 余 红,沈珍瑶.三峡水库大宁河流域非点源污染参数的不确定性分析 [J]. 中国环境科学, 2007,27(4):554-558.

[8] Mckay M D, Beckman R J, Conover W J. A comparison of three

methods for selecting values of input variables in the analysis of

output from a computer code [J]. Technometrics, 2000,42(1):55-61. [9] 刘纪涛,刘 飞,张为华.基于拉丁超立方抽样及响应面的结构模糊分析 [J]. 机械强度, 2011,33(1):73-76.

[10] 李一平,逄 勇,罗潋葱.波流作用下太湖水体悬浮物输运实验及模拟 [J]. 水科学进展, 2009,20(5):701-709.

[11] Li Y P, Acharya K, Mark C S, et al. Spationtemporal patterns in nutrient loads, nutrient concentrations, and algal biomass in Lake Taihu, China [J]. Lake and Reservoir Management, 2011,27(4):298-309.

[12] Li Y P, Acharya K, Yu Z B. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China [J]. Ecological Engineering, 2011,37(2):325-334.

[13] 施小青,吴吉春,姜蓓蕾,等.基于LHS方法的地下水流模型不确定性分析 [J]. 水文地质工程地质, 2009,2:1-6.

[14] Manache G, Melching C S. Sensitivity analysis of a water-quality modeling using Latin Hypercube Sampling [J]. Journal of Water Resources Planning and Management, 2004, 130(3):232-242.

[15] Pan F, Ye M, Zhu J T, et al. Incorporating layer- and local-scale heterogeneities in numerical simulation of unsaturated flow and tracer transport [J]. Journal of Contaminant Hydrology, 2009, 103(3/4):194-205.

[16] Pan F, Zhu J T, Ye M, et al. Sensitivity analysis of unsaturated flow and contaminant transport with correlated parameters [J]. Journal of Hydrology, 2011,397(3/4):238-249.

[17] 李一平,唐春燕,余钟波,等.大型浅水湖泊水动力模型不确定性

和敏感性分析 [J]. 水科学进展, 2012,23:271- 277.

Uncertainty and sensitivity analysis of input conditions in large shallow lake hydrodynamic model.

LI Yi-ping1,2,3*,

QIU Li1,2, TANG Chun-yan1,2, BU Min-sheng4, TIAN Wei5, YU Zhong-bo3, Kumud Acharya3(1.Key Laboratory of Integrated Regulation and Resources Development of Shallow Lakes, Ministry of Education, Hohai University, Nanjing 210098, China；2.College of Environment, Hohai University, Nanjing 210098, China；3.State Key Laboratory of Hydrology Water Resources and Hydraulic Engineering, Nanjing 210098, China；4.College of Mechanical and Electrical Engineering, Hohai University, Nanjing 210098, China；5.Hydrology and Water Resources Investigation Bureau of Jiangsu Province, Nanjing 210029, China). China Environmental Science, 2014,34(2)：410～416

Uncertainty and sensitivity analysis of four important input conditions on the Environmental Hydrodynamic Fluid Code (EFDC) model results (i.e., water level, water age and currents) was investigated for a large shallow lake, Lake Taihu, China. The four input conditions included three boundary conditions (i.e., inflow/outflow, wind speed, wind direction) and an initial condition (i.e., initial water level). The Latin Hypercube sampling (LHS) as a global sensitivity method was used to estimate the uncertainty and sensitivity from the four input conditions. The results showed that uncertainties in the hydrodynamic process existed due to the uncertainties of model input conditions. Among the four input conditions, the initial water level was the most sensitive factor for the simulated water level and water age with the uncertainty contributions of 85.73% and 66.125% respectively, while it had barely 3% contributions to vertical averaged velocity. Wind speed played a significant role in the uncertainty of the velocity in the surface layer with a sensitivity coefficient of 58.70%, while it only had 5.25% and 3.00% contributions to the simulated water level and water age, respectively. Additionally, there was a similar impact of the four input conditions on the uncertainty of velocities in different layers. The four input conditions’ contributions to the velocities were as follows: wind speed (55%～60%) > wind direction (10%～15%) > initial water level ≈ inflow/outflow (1%～5%). Thus, the results provided reliable information forthe model prediction of large shallow lakes like Lake Taihu. For different output targets, improving the precision of the input conditions with priority can efficiently enhance the precision of the hydrodynamic model.

input conditions；uncertainty analysis；sensitive analysis；environmental fluid dynamic code (EFDC)；large shallow lake

X143

：A

：1000-6923(2014)02-0410-07

李一平(1978-),男,湖北荆州人,副教授,博士,主要从事河湖富营养化机理及水环境数学模型研究.发表论文50余篇.

2013-06-08

江苏省高校“青蓝工程”;河海大学创新人才计划;国家“973”项目(2010CB951101);国家自然科学基金(51379061);江苏省自然科学基金(BK20131370)

* 责任作者, 副教授, liyiping@hhu.edu.cn