连续型全概率公式及其应用

王丰效

(喀什师范学院数学系，新疆 喀什 844000)

全概率公式是概率论的重要公式之一，也是教学中的重点与难点.全概率公式［1］是间接计算概率的重要公式.它是一种介绍如何化解复杂事件的概率计算为一系列互不相容的简单事件概率计算的方法.全概率公式内涵丰富，应用广泛，许多学者对其进行了深入的研究［2-5］.利用概率论的基本理论和方法解决概率问题的技巧也在相关文献中被讨论［6-11］.本文利用随机事件的全概率公式，分别给出分布函数形连续型随机变量的全概率公式，并给出了离散型全概率公式和连续型全概率公式的应用.

1 离散型全概率公式和连续型全概率公式

定理1［1］设S为试验E的样本空间，B1，B2，…是一列互不相容的事件，且∪∞i=1Bi=S，则对任意事件A有

利用定理1，容易将全概率公式推广到随机变量的情形，从而可得到下面的两个定理.

定理 2［2］设(X，Y)为二维离散型随机变量，一切可能取值为(xi，yj)，i，j=1，2，…，则有

称(1)为离散型全概率公式.

定理3 设(X，Y)为二维连续型随机变量，X，Y的分布函数分别为FX(x)，FY(y)，则有

称(2)为连续型全概率公式.

证明:设(X，Y)为二维连续型随机变量的联合密度函数为 p(x，y)，X，Y的边际分布函数分别为FX(x)，Fy(y)，则

由(2)利用对立事件的概率性质易得

推论1 设(X，Y)为二维连续型随机变量，X，Y的分布函数分别为FX(x)，FY(Y)，则有

推论2 设(X，Y)为二维连续型随机变量，则随机变量X和Y相互独立的充分必要条件是对任意x，y有P(X≤x|Y=y)=P(X≤x).

2 连续型全概率公式的应用

2.1 随机变量函数分布

下面通过几个例子说明连续型全概率公式在解决概率问题的应用.首先利用连续型全概率公式给出两个独立连续型随机变量的数分布的计算公式.

例1 设X和Y是两个相互独立的连续型随机变量，X，Y的密度函数分别为pX(x)，pY(y).则随机变量Z=X+Y的密度函数为

例2 设X和Y是两个相互独立的连续型随机变量，X，Y的密度函数分别为pX(x)，pY(y).则随机变量Z=X－Y的密度函数为

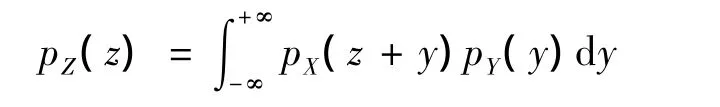
例3 设X和Y是两个相互独立的连续型随机变量，X，Y的密度函数分别为pX(x)，pY(y).则随机变量Z=X/Y的密度函数为

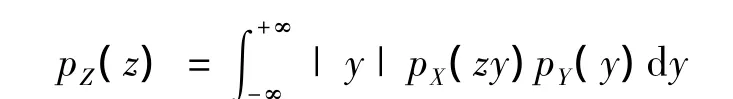
解 随机变量Z=X/Y的分布函数为

例4 设X和Y是两个相互独立的连续型随机变量，X，Y的密度函数分别为pX(x)，pY(y).则随机变量Z=XY的密度函数为

上述4个例子实际上是分别给出了两个独立随机变量和、差、积、商的函数密度的计算公式.对于非独立的情形也可以类似讨论.

例5 设(X，Y)为二维连续型随机变量的联合分布函数为F(x，y)，X，Y的边际分布函数分别为FX(x)，FY(y)，则随机变量Z=X+Y的分布函数和密度函数分别为

例6 某射手进行射击，每次射击击中目标的概率为p(0＜p＜1)，射击进行到击中目标两次时停止.求第二次击中目标所需射击次数的分布列.

解 假设第一次击中目标时的射击次数为X，第二次击中目标时的射击次数为Y，则随机变量Y的可能取值为2，3，….有离散型全概率公式(1)可得

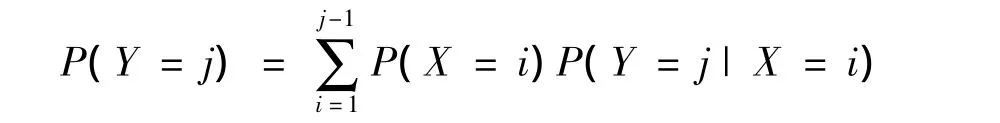
由几何分布的特性可知 P(Y=j|X=i)=p(1 － p)j－i－1，故

2.2 随机变量相关的概率计算

利用连续型全概率公式可以计算与两个随机变量相关的形如P(X≤g(Y))概率计算问题.

例7 (Buffon投针问题).平面上画有等距离平行线，平行线间的距离为a(a＞0)，向平面任意投掷一枚长为l(l＜a)的针，求针与平行线相交的概率.

解 设针的下端与下方一条平行线间的距离为X，针与平行线的夹角为Y，则随机变量X服从均匀分布，随机变量Y服从区间［0，π］上的均匀分布.

而针与平行线相交等价于a－X≤lsinY.由投掷的随机性可知随机变量X和Y相互独立.故针与平行线相交的概率为

例8 假定两个元件的寿命X，Y分别服从参数为λ和μ的指数分布，且X，Y相互独立，求P(X≤Y).解 由连续型全概率公式有

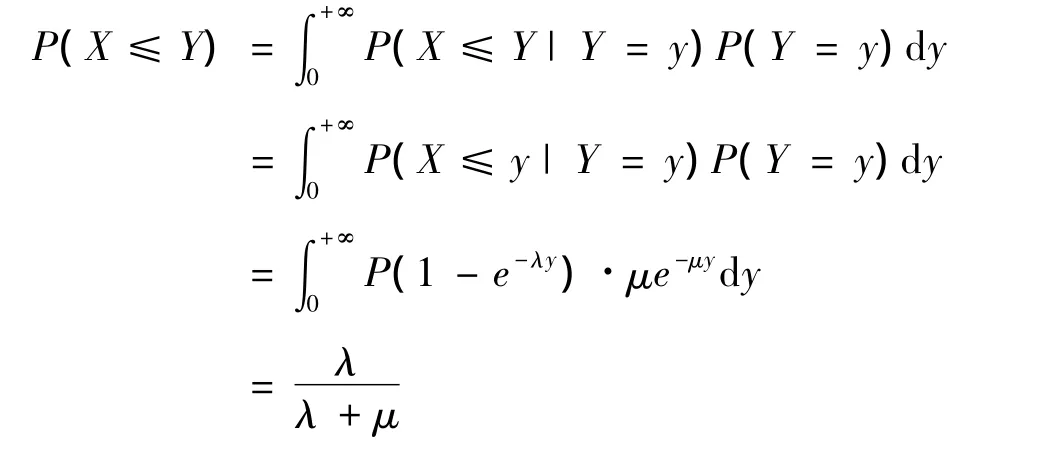
［1］魏宗舒.概率论与数理统计教程［M］.北京:高等教育出版社，1983.

［2］陈光曙，王新利.全概率公式的推广及应用［J］.高等数学研究，2010，(5):53 ～54.

［3］唐旭晖，李冱岸，段利霞.全概率公式的推广与应用［J］.高等数学研究，2011，(7):51～52.

［4］田丽娜，张 静，刘玉胜.全概率公式的推广与应用［J］.甘肃高师学报，2009，(5):84～85.

［5］张 丽，闰善文，刘亚东.全概率公式的与叶斯公式的应用及推广［J］.牡丹江师范学院学报(自然科学版)，2005，(1):15～17.

［6］周茂袁，王秀丽，李雪艳.特征函数的一种新解释及其应用［J］.吉林师范大学学报(自然科学版)，2008，29(2):37～41.

［7］阿布力克木·阿布都依木.三维随机变量的变量替换定理及应用［J］.吉林师范大学学报(自然科学版)，2013，34(4):90～92.

［8］潘素娟，林丽钦.概率统计中自由度的理解与应用［J］.吉林师范大学学报(自然科学版)，2013，34(4):138～140.

［9］王丰效.描述随机变量分布的新函数［J］.沈阳师范大学学报，1996，14(4):8～10.

［10］周概容.概率论与数理统计［M］.北京:高等教育出版社，1985.

［11］王丰效.指数母函数在数学期望计算中的应用［J］.重庆文理学院学报，2014，33(2):33～35.