多平台快速成型软件设计

冯清秀 阿占文

(华中科技大学机械科学与工程学院，湖北 武汉 430074)

快速成型技术是目前制造领域的热点问题，该技术的特点是对计算机软件有高度依赖性。目前国内有部分快速成型设备生产企业拥有自主研发的软件，但大部分仍依赖国外软件，快速成型软件设计成为限制其发展的重要因素，在国内已有的快速成型产品成本中，软件部分占了很大比例。在该项技术快速发展的将来，为了提高产品竞争力，降低成本，自主设计研发成型软件是一个趋势，而如何提高稳定性以及算法效率、软件优化是最关键的问题［1-2］。

1 软件总体设计

1.1 人机界面及软件功能设计

1.1.1 人机界面设计

对快速成型设备来说，人机交互界面是人与设备之间的桥梁，一个稳定、友好、高效的人机交互界面可以极大地增强产品的用户体验。本文设计的软件人机主界面由6 个区域组成，分别是:标题栏、文字菜单、快捷菜单、主视图区、整体信息显示区、概要信息显示区。如图1、图2 所示。标题栏可以显示所打开文件的路径和文件名，快捷菜单可供用户快速找到常用操作按钮，主视图区是基于OpenGL 的模型显示窗口，可以进行缩放、平移、旋转操作，还可以根据用户选择进行主视图、俯视图、右视图等的视图切换，或者根据用户选择进行STL、轮廓、填充路径等模型切换。

此外还有一个用于分层显示的子界面，在这个子界面中可以查看整个模型的某一层的具体信息，如:轮廓形状、填充路径、面积、填充间距、偏置次数等，还可以进行加工仿真和动画播放，直观地观察各层加工路径和动画仿真，检查分层及路径生成中的错误。

1.1.2 软件功能设计

本文所设计的软件可以运行在主流的Windows、Linux 和Mac 三个系统平台，可以实现以下功能:

(1)STL 模型的缩放、平移、旋转显示;

(2)按用户指定厚度、范围和方向进行分层;

(3)按用户指定填充间距和轮廓偏置次数，进行分区复合填充。判别内外环，轮廓分组以及路径优化;

(4)输入/出CLI 文件和支撑添加;

(5)加工路径仿真和分层显示。

各个功能如图3 所示。

1.2 面向对象的数据结构设计

快速成型软件需要管理的数据有模型的三角面片顶点、轮廓交点、填充线段等，数据量非常大(一般零件都具有上千个三角面片)。一个合理的数据结构不仅可以提高算法效率，还会使程序清晰明了，提高可读性，降低软件开发难度。本文运用面向对象的编程方式，设计了7 个类来管理这些数据，分别是顶点类(QVertex)、三角形类(QTriangle)、模型类(QBody)、层类(QLayer)、轮廓类(QContour)、扫描线类(QScan-Path)和填充线类(QFillPath)。数据结构如图4 所示。图4 中箭头方向表示了类之间的包含关系，如三角面片类包含了顶点类，模型类包含了层类和三角面片类，层类包含了轮廓类，轮廓类包含了扫描线类，扫描线包含了填充线类，这也完全符合人的思维:将一个模型划分为几个具体模块，这是数据结构的定义依据。

因为在读取模型文件之前不知道有多少个三角面片，同样在分层之前也无法得知会分为多少层，而在确定对象的值之前需要提前分配内存，如果用数组则需要二次或者多次分配。为解决此问题，运用了C++语言中的Vector 类模板，它可以动态分配内存，存取极其方便。本软件中顶点对象(vector)、三角面片对象(triangle)、层对象(layer)、轮廓对象(contour)、扫描线对象(scanpath)、填充线对象(fillpath)都定义为Vector 类型。在面向对象编程中，类的属性(变量)代表了这个类所包含的变量，是各个类之间沟通的桥梁，也称类的接口。类的方法(函数)代表了这个类能进行的操作，即类的功能函数。方法和属性构成了一个类［3］，本软件中几个核心类的方法和属性如图5 所示。

2 软件关键功能的实现方法

2.1 读入STL 文件及显示和分层

STL 文件中每个顶点坐标之前都有一个vertex 关键词，根据该特点可以逐行检测STL 数据，取vertex 关键词之后的3 个数为一个顶点，构成QVertex 对象，每3 个QVertex 对象构成一个QTriangle 对象，直至文件结束。此时QTriangle 对象存在了QVertex 对象中，而QVertex 对象又存在了QBody 对象中，层层关联，在模型显示时则做相反的操作，以body-＞triangle_all［triangle_count］-＞vertex［vertex_count］的方法取得所有顶点坐标。显示部分是利用Qt 支持的OpenGL 图形库设计的，投影模式设置为正射投影，原点在屏幕中央。

分层过程是将一个三维模型转化为二维平面图形的过程，关键在于求出每个分层面与三角面片的交点，从而由这些交点组成轮廓。如图6 所示，以z 向分层为例，按用户设定的厚度，从起点到终点确定出每个分层面的z 值，只有三角形三个顶点的z 值的最大、最小值满足条件:Zmin＜z ＜Zmax时，才会有交点，利用这个特点，首先找出所有本层符合该条件的三角面片再求交点可以提高效率，利用式(1)求出交点的坐标值［1］。

式中xp，yp，zp(zp=zvalue)为所求交点坐标，z1即上文提到的Zmin，z2为Zmax，x、y 与z 类似。为保证所求交点都是按相邻顺序存储在轮廓对象中，每求一个交点就要寻找与之相邻三角面片。根据STL 数据中的共顶点规则［4］，查找具有相同顶点的面片，并根据找到的面片的3 个顶点的z 值替换Zmin和Zmax，代入式(1)，直至所有符合条件的面片都遍历一遍。有些模型不止一个轮廓，此时求出一个完整轮廓后发现还有面片没有求交，需要继续以上过程。分层过程总结如下:

(1)按指定厚度和范围确定每层的zvalue;

(2)建立一个新轮廓，取一个面片，找出各个坐标最值，利用式(1)求出一个交点;

(3)找相邻面片，重新找到各个坐标最值，利用式(1)求出一个交点，直至相邻面片遍历完毕;

(4)若符合条件的面片遍历完毕，但还有其它面片未求交，转(2);

(5)若所有面片遍历完毕，结束分层。

2.2 轮廓分区复合填充

轮廓填充是快速成型的核心算法之一，其方法有:平行填充、环形填充、光栅填充等。轮廓的分区复合填充是一种结合了前两者的方法，有效地减小了应力造成的零件变形，同时因为避免了环形填充带来的轮廓偏置产生的自相交等问题所以算法简单，易于实现。具体思路是:将所有轮廓划分成许多个单连通区域，在此区域内将所有内外轮廓偏置4～6 次，然后再进行平行填充，为避免频繁跨越内腔，再将填充线分区，如图7 所示。其中粗实线表示内外轮廓，细实线表示填充线，内外轮廓均偏置3 次(第三次偏置只做求交运算以确定平行填充线端点)，然后分成上、中左、中右、下4 个区填充。这就涉及到了内外环的判别及分组算法、轮廓偏置算法以及最后分区之后的路径优化算法。下面是这几个算法的说明。

2.2.1 轮廓分组

在许多个轮廓中划分出单连通区域是分区复合填充的基础，算法步骤如下:

(1)计算每个轮廓被其他轮廓包含的次数;

(2)根据被包含奇数次为内轮廓，偶数次为外轮廓的原理，判别每个轮廓是内轮廓还是外轮廓;

(3)一个轮廓组只有一个外环，所以对于一个外轮廓，如果其被包含次数为N 次，而一个内轮廓的被包含次数为N-1 次，那么这两个轮廓为一组;

(4)按步(3)继续找出本外环下所有内轮廓，成为一个完整的轮廓组。

文献［5］给出了上述算法，但没有给出该算法的基础:轮廓包含关系判断方法。因为轮廓与轮廓之间不会有交点，所以取轮廓上一点判断是否在另一个外轮廓内即可判定轮廓包含关系。利用射线法可以判断一点是否在多边形内，即做射线与多边形轮廓求交，统计交点个数，如果是偶数则在多边形外，奇数则在多边形内。关于顶点法的实现代码很多，效率也有很大差异。本文中用的代码如下:

2.2.2 轮廓偏置及填充线分区

轮廓偏置算法是数控加工领域常用的而又复杂的基本算法，因为涉及到复杂凹多边形以及轮廓偏置以后的自相交去除问题，很多文献提出的算法不适用于一般情况。本文首先用求取偏置法向量的方法得到偏置轮廓，其次根据文献［6］提出的算法去除自相交环。如图8 所示，先约定在y 轴向上的坐标系中，多边形轮廓如果是外环就按逆时针存储，内环相反。是原轮廓内环，是偏置以后的轮廓，向量en是偏置法向量，其正方向按右手定则约定:按逆时针旋转90°与en重合，那么en即为正向。依此法向量的正向，沿轮廓边向量方向行走时，轮廓区域总是在法向量的正向，可知其满足不等式(2)。设直线方程由式(3)给出，则en的方程由(4)给出，并且有式(5)成立。

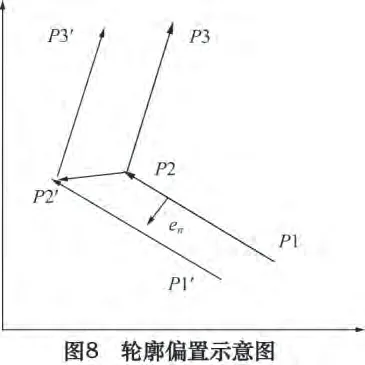
以P1(x1，y1)，P2(x2，y2)代入式(3)，结合式(2)、(4)可以求出a 和b。此时的直线方程由式(6)给出，其中，dist 为偏置距离。同理可求出'的方程，如式(7)。直线'的交点即为P2 的偏置点P2'，其坐标由式(8)给出，其中l1=

对每一个轮廓边由式(8)求出所有偏置线段，只要外环是按逆时针存储，那么必然向内偏置，内环如果是按顺时针存储，必然是向外偏置。但在偏置后不可避免地产生自相交轮廓，此时必须去除无效环。文献［6］给出了一种有效的方法。

得到偏置轮廓后，按填充间距求出均匀分布在外轮廓内的扫描线，然后对所有扫描线段进行分组，如图7 中分为4 组填充，软件中不同的区域填充线显示不同的颜色，以便区分。文献［7］提出了基于交点扫描线与轮廓交点数目的分组方法，总结如下:

(1)求所有扫描线与轮廓交点;

(2)由上往下(或由下往上)依次检测每个扫描线的交点数目，假设第N 条扫描线有m 个交点，第N +1条扫描线也有m 个交点，那么属于同组，第N+2 条扫描线有n(n≠m)个交点，那么重新建立一个组，依次类推。如图7 中由上到下分3 组;

(3)对一组有m(m ＞4)个交点的扫描线，第1、2个交点为一组填充线，第3、4 个为另外一组填充线，直至第m-1 和m 个最后一组填充线。

2.2.3 基于距离判定法的路径优化

填充线分组后要进行路径优化，在上文图7 中，平行填充时分了4 个区，实际加工时必须先确定这4 个区的填充顺序，称为路径优化问题。文献［8］提出了一种基于距离判定的路径优化方法，思路如下:

(1)确定每个填充区域的首末填充线段的4 个端点，如图7 中标号A 到P 共16 个点放入集合NotUsed;

(2)开始填充时先取一个端点，将其放入集合Used，同时从NotUsed 删除;

(3)填充到一组填充线最后一点，取当前所在点(必在NotUsed 中)，求其与NotUsed 集合中剩余所有点的距离，最短者为下一填充区起点;

(4)每走过一个端点就将其放入集合Used，同时从NotUsed 删除;

(5)若NotUsed 集合变成空集时表明所有区域填充完毕，否则转(3)。

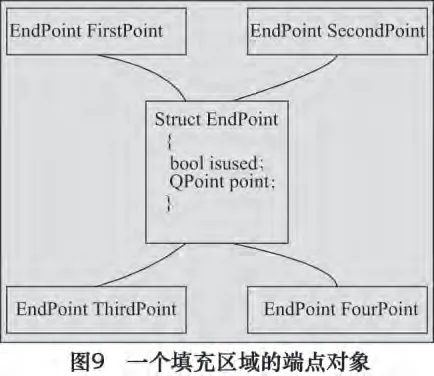
实际在软件中实现时还要解决每个填充区域4 个端点如何连接的问题，如在图7 中，先按A-B -C -D的顺序填充了最上面一个区的4 个点，那么下一个要填充的区的最近点为J，此时要按J -I -K -L 的顺序填充。为解决此问题，给每个区域的4 个端点从左到右，从上到下建立如图9 所示4 个对象。在最极端的情况下，如果某个组只有一条填充线，也就是说只有两个端点无法建立4 个对象。为解决此种情形，预先假设有4 个端点，但其isused 属性预置为真(true)，然后分别求端点，再将isused 属性置为假(false)，这样使得只有两个端点的填充组虽然有4 个对象，但不参与填充。总结起来可分为4 种情况:

(1)若以FirstPoint 为起点，则往下填充，奇数行时调换首末两个端点。

(2)若以SecondPoint 为起点，则往下填充，偶数行时调换首末两个端点。

(3)若以ThirdPoint 为起点，则往上填充，奇数行时调换首末两个端点。

(4)若以FourthPoint 为起点，则往上填充，偶数行时调换首末两个端点。

3 结语

本文所设计的软件读取一个具有1620 个面片的齿轮泵箱体零件的模型，其尺寸为长× 宽× 高:100 mm×110 mm×90 mm，按0.8 mm 的厚度分为113 层，在2G CPU 和2G 内存条件的计算机上用时6 s。填充时轮廓偏置3 次，间距为0.3 mm，并进行路径优化，在同一计算机上用时4 s。执行效率比较高，可以满足快速成型的要求。再分层查看界面，可进行仿真，实际观察加工轨迹，如图10 所示，本层面积为3096.4 mm2，共分24 组填充，路径规划完全符合距离最短原则。

添加支撑体也是快速成型的关键问题。本文取“BOX”型支撑方式，此种支撑算法简单但是材料利用率低下。文献［10 -11］提出了一种基于特征的向下添加支撑的方法，但实现起来比较复杂，文献［12 -13］提出了自动生成支撑的思想。如果按零件的形状，采用不同的填充方式，而非固定的一种，会极大地提高成型质量。采用环形填充叶，为了避免算法过于复杂，可借助已经成熟的第三方的算法库来实现，也不失为一种有效的解决途径。

［1］刘伟军.快速成型技术及应用［M］.北京:机械工业出版社，2005:39 -43.

［2］朱林泉，白培康，朱江淼.快速成型与快速制造技术［M］.北京:国防工业出版社，2003:59 -66.

［3］钱能.C++程序设计教程［M］.北京:清华大学出版社，2004:232-257.

［4］赵吉宾，刘伟军，王越超，等。基于STL 文件的实体分割算法研究［J］.机械科学与技术，2005，24(2):131 -134.

［5］蔡道生，史玉升，黄树槐，等.快速成形技术中轮廓环的分组算法及其应用［J］.华中科技大学学报:自然科学版，2004，32(1):7 -9.

［6］Xiaorui Chen，Sara McMains.Polygon Offsetting by Computing Winding Numbers［C］.//2005 ASME International Design Engineering Technical Conferences ＆amp;Computers and Information in Engineering Conference (IDETC/CIE2005)，vol.1.2005:6009 -6019

［7］史玉升，钟庆，陈学彬，等.选择性激光烧结新型扫描方式的研究及实现［J］.机械工程学报，2002，38(2):35 -39.

［8］李伟.熔丝沉积成形填充路径优化及其软件研究［D］.武汉:华中科技大学，2005.

［9］程艳阶.选择性激光烧结激光扫描路径的研究与开发［D］.武汉:华中科技大学，2004.

［10］洪军，李涤尘，唐一平，等.快速成型中的支撑结构设计策略研究［J］。西安交通大学学报，2000，34(9):58 -61，76.

［11］董未名，严冬明，周登文，等.基于CAD 模型的直接快速成型软件［J］.计算机辅助设计与图形学学报，2004，16(3):360 -367.

［12］史晓楠.CLI 文件正确性检验与支撑设计系统研究［D］.西安:西安科技大学，2006.

［13］纪良波，周天瑞，溍海鹏，等.熔融沉积快速成型软件系统的开发［J］.塑性工程学报，2009，16(3):192 -197.