Study of recursive model for pole-zero cancellation circuit∗
2014-04-24ZHOUJianBin周建斌HONGXu洪旭WANGRenBo王仁波ZHOUWei周伟HUYunChuan胡云川WANXinFeng万新峰andDUXin杜鑫
ZHOU Jian-Bin(周建斌),HONG Xu(洪旭),WANG Ren-Bo(王仁波),ZHOU Wei(周伟),HU Yun-Chuan(胡云川),WAN Xin-Feng(万新峰),and DU Xin(杜鑫)
1College of Nuclear Technology and Automation Engineering, Chengdu University of Technology,Chengdu 610059,China
2Engineering Research Center of Nuclear Technology Application, Ministry of Education,East China institute of Technology,Nanchang 310013,China
Study of recursive model for pole-zero cancellation circuit∗
ZHOU Jian-Bin(周建斌),1,2HONG Xu(洪旭),1,†WANG Ren-Bo(王仁波),2ZHOU Wei(周伟),1,2HU Yun-Chuan(胡云川),1WAN Xin-Feng(万新峰),1and DU Xin(杜鑫)1
1College of Nuclear Technology and Automation Engineering, Chengdu University of Technology,Chengdu 610059,China
2Engineering Research Center of Nuclear Technology Application, Ministry of Education,East China institute of Technology,Nanchang 310013,China
The output of charge sensitive amplif i er(CSA)is a negative exponential signal with long decay time which will result in undershoot after C-R differentiator.Pole-zero cancellation(PZC)circuit is often applied to eliminate undershoot in many radiation detectors.However,it is diff i cult to use a zero created by PZC circuit to cancel a pole in CSA output signal accurately because of the inf l uences of electronic components inherent error and environmental factors.A novel recursive model for PZC circuit is presented based on Kirchhoff’s Current Law(KCL)in this paper.The model is established by numerical differentiation algorithm between the input and the output signal.Some simulation experiments for a negative exponential signal are carried out using Visual Basic for Application(VBA)program and a real x-ray signal is also tested.Simulated results show that the recursive model can reduce the time constant of input signal and eliminate undershoot.
Pole-zero cancellation,Numerical analysis in time domain,Numerical simulations
I.INTRODUCTION
The detector signal needs to be amplif i ed before digitized in radiation detection technique.There are two types of amplif i ers,i.e.,preamplif i er and amplif i er.The preamplif i er is located as close as possible to the detector.The main function of a preamplif i er is to maximize the signal-to-noise ratio and to provide a low impedance source for the amplif i er[1].It also should provide a high impedance load for the detector.The amplif i er is applied to amplify and shape the output signal of preamplif i er.
CSA is extensively used in X-ray f l uorescence analyzer and well logging system as a preamplif i er with the advantages of lownoiseandeff i cientperformanceathighcountingrates.The CSA output is a two-component signal,which consists of a rapidly rising edge and a followed slow trailing edge that decay back to baseline with the long time constant of the CSA, instead of an ideal step signal.CSA output pulses can pile up onthetailsofpreviouspulsesandcausebaselinedrifting,characteristic peak drifting and poor resolution due to high counting rates.In a worse case,the pulse resulting from pile-up pulse may block the amplif i er of next stage.In multi-channel analysis(MCA),PZC technique is used to reduce the width of negative exponential signals[2,3],which can decrease the possibility of pulse pile-up,and keep good energy resolution at high counting rates.A PZC circuit consisting of one capacitor of 24pf and twenty PMOS transistors connected in parallel was designed to reduce the effect of pile-up[4].Pawel Grybos proposedacontinuousCSAfeedbackresetsystemwithanovel architecture for PZC circuit in high rates of input pulses condition[5–7].This system reduced the inf l uence of a DC voltageshift resulting from high rates of input pulses on CSA feedback resistance and the PZC circuit.Seinoet al.used an alternative technique instead of pulsed bias voltage shutdown technique to avoid degrading the energy resolution in high counting rates condition without a PZC circuit[8].However,it is diff i cult to use a zero in the transfer function expressed in Laplace transform to cancel a pole presented in CSA output signal accurately by using PZC circuit because of the inf l uences of electronic components inherent error and environmental factors.A novel recursive model for PZC circuit is presented to eliminate undershoot and reduce the width of CSA output signals in this paper.
II.POLE-ZERO CANCELLATION CIRCUIT
Figure 1 shows the CSA analog circuit,which consists of a feedback capacitance Cf,a feedback resistance Rf and a operational amplif i er.A current signal generated in the detector is integrated on Cf,and Rf is used for discharging Cf to avoid the amplif i er saturation when a series of charge pulses come to the input of the CSA[9].
AsG·Cf≫Ci+Cf,whereGis the amplif i er open loop gain,Ciis the input capacitor of CSA,the CSA input voltage signal can be given by Eq.(1),andQrepresents the total charge collected in the detector and is proportional to the energy of deposited into detector,τfis the time constant withτf=Rf·Cf.
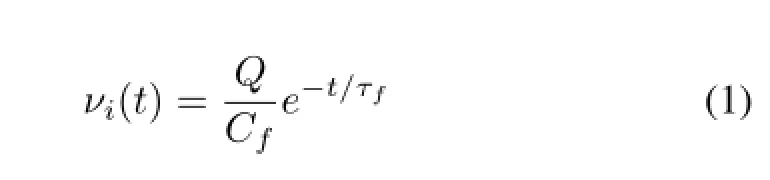
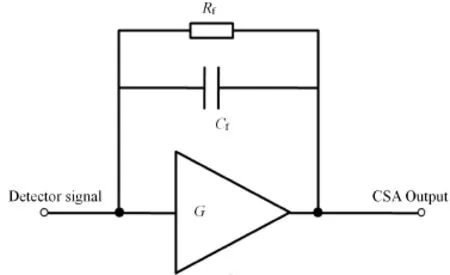
Fig.1.Scheme of CSA.
Rfhas an intrinsic noise(Johnson noise)associated with it.The noise can be minimized by selecting a higherRf.For the applications of extracting detector output signal(small signal)and minimizing the noise,the value ofRfis often chosen in the M Ohm range.So the time constantτfis relatively long[6].The long time constant can induce to long lasting undershoot after the C-R shaper causing overloading in the next amplif i er stage and make the amplif i er working in non-linear region losing the ability of amplif i cation for small signals.It can also cause pulse pile-up deteriorating the energy resolution[10].
PZC circuit can eliminate undershoot which results from long time constant of CSA[11].Fig.2 illustrates a PZC circuit[12].The input signal is def i ned as vi and the output signal as vo.RPZis the variable resistor,which can eliminate the undershoot by adjusting properly.
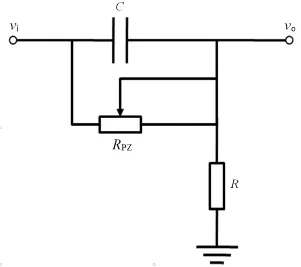
Fig.2.Scheme of PZC circuit.
Eq.(1)can be described as Eq.(2)according to Laplace transform.
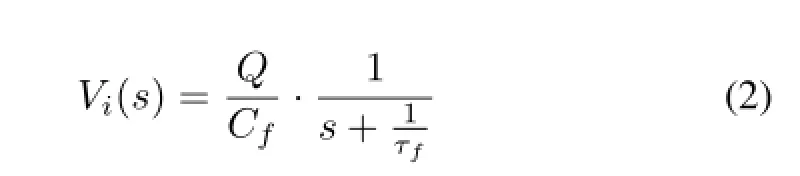
The transfer function of Fig.2 can be represented as
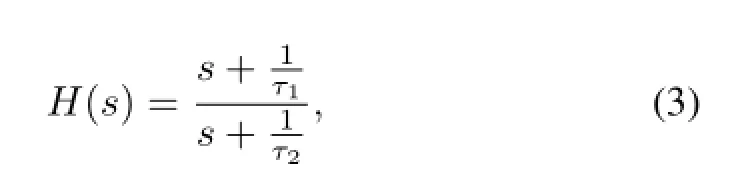
whereτ1=RPZ·C,τ2=(R//RPZ)·C.For the Eq.(2) and(3),the output signal in Fig.2 can be expressed as
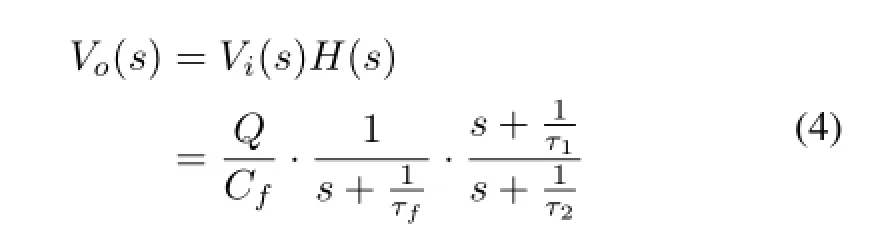
Thecancellationrequirementleadstotheconditionτ1=τf. Eq.(4)can be written as
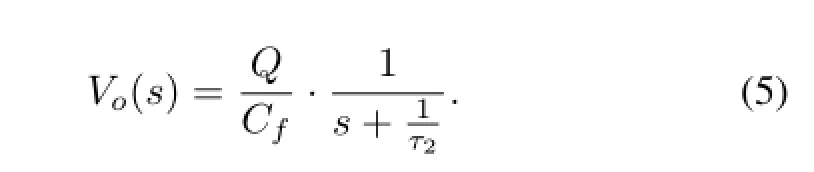
The time domain outputvo(t)can be obtained through the inverse Laplace transform as
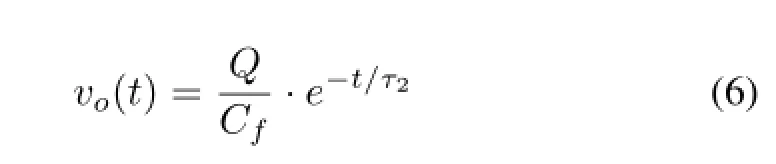
So,the CSA output becomes a negative exponential signal with shorter decay time(time constant isτ2)whenτ1=τf.
III.NUMERICAL ANALYSIS AND SIMULATIONS
Laplace transform makes the signal convenient for analysis.However,it is diff i cult for some complex signals to convert from time domain to Laplace domain and it could lose the time-domain characteristics by using Laplace transform. A novel recursive model for PZC circuit is implemented based on the analysis of digital C-R shaping method[13]and digital Sallen-Key low-pass f i lter[14].
A.Numerical recursive root
According to KCL,which states that the sum of current into a junction equals the sum of current out of the junction,the voltage transmission in Fig.2 can be described by the following equations:
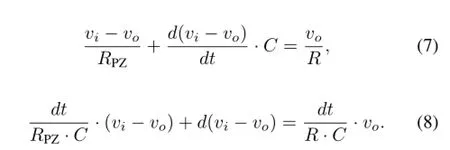
Analog signal can be converted into discrete series with small time interval by using high-speed ADC.A f i rst-order numerical differentiation method is used to solve Eq.(8).Lettingvi=x[n],vo=y[n],dt=Δt,Eq.(8)can be rewritten as
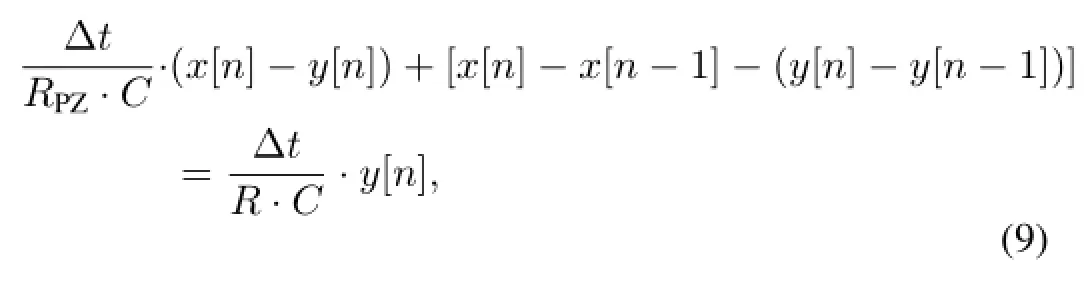
where Δtis the time interval fromx[n−1]tox[n]or the sampling time period of the high-speed ADC,x[n]andy[n] are the input and output data series,respectively.Lettingk1= Δt/(RPZ·C),k2=Δt/(R·C),Eq.(9)can be simplif i ed to
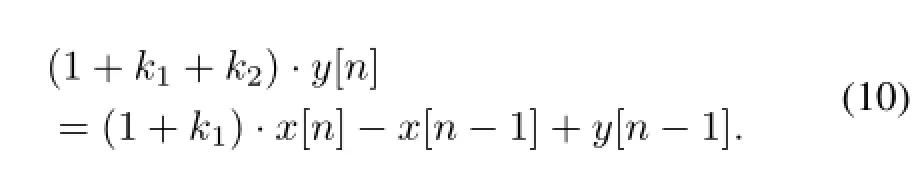
Eq.(10)can be written as Eq.(11)based on mathematical equivalence transformation.
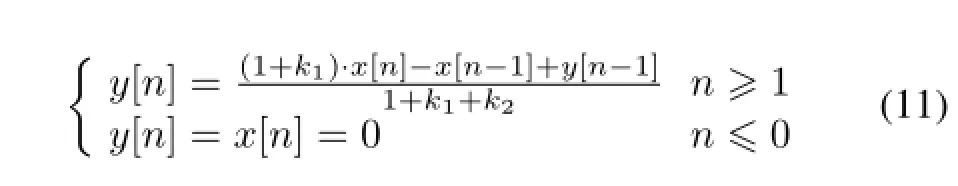
Eq.(11)is the numerical recursive root corresponding to the PZC circuit in Fig.2 and it is also the recursive model for PZC circuit.The recursive PZC model processing of the CSA output signal can be implemented by recursive-calling of Eq.(11).Different type of output signals can be acquired at differentk1andk2,the shaping parameters of the recursive PZC model.
An accumulation depending on a standard negative exponential signal is carried out to verify the model.Def i nevi=A·e−t/τ,where A represents the amplitude of input signal,τis time constant.Takingviinto Eq.(7),a differential equation can be described as
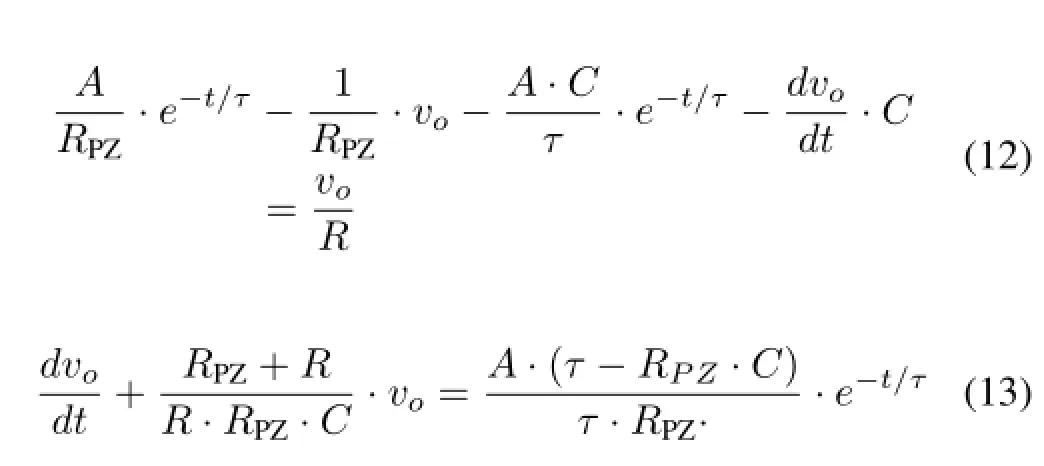
LetRPZ·C=τby adjustingRPZ.Eq.(13)can be written as Eq.(14).
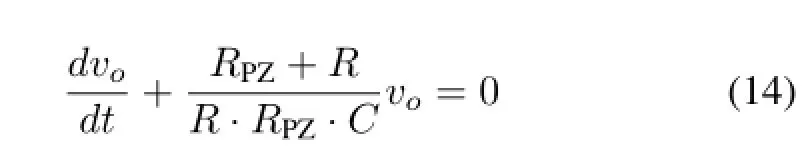
Lettingvo=y,yis def i ned as the output signal of PZC circuit at a certain time,Eq.(14)can be converted into
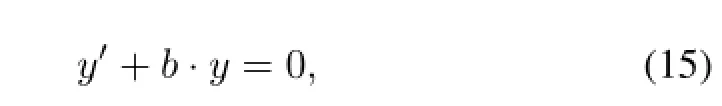
whereb=(RPZ+R)/(R·RPZ·C).Eq.(15)is a f i rst-order linear homogeneous equation,the root of which can be def i ned as

whereCis a constant.The output of PZC circuit in time domain can be obtained according to Eq.(16).

From the equation above,it can draw a conclusion that the output of recursive PZC model is a negative exponential signal without undershoot and the time constant is(R//RPZ)·Cwhile the input is a standard negative exponential signal.This is equivalent to the conclusion drawn from Eq.(6).It is indicated that the model deduced in time domain has the same signal processing function as a real PZC circuit does.In order to test this new model,some computer simulations are carried out and a real x-ray signal test is also performed.
B.Computer simulations
AcomputersimulationplatformisdevelopedwithVBAlanguage.TherecursivePZCmodelanditsinputsignalareimplemented through program code.The simulations include four phases:
1.A standard negative exponential signal simulation.A standard negative exponential signal can be obtained with Eq.(18):

whereArepresents the amplitude of the standard negative exponentialsignal,τis decay constant.Fig.3 shows the standard negative exponential signal withA=2000,τ=200 which ref l ects the time constant is 10µs as Δt=50ns.
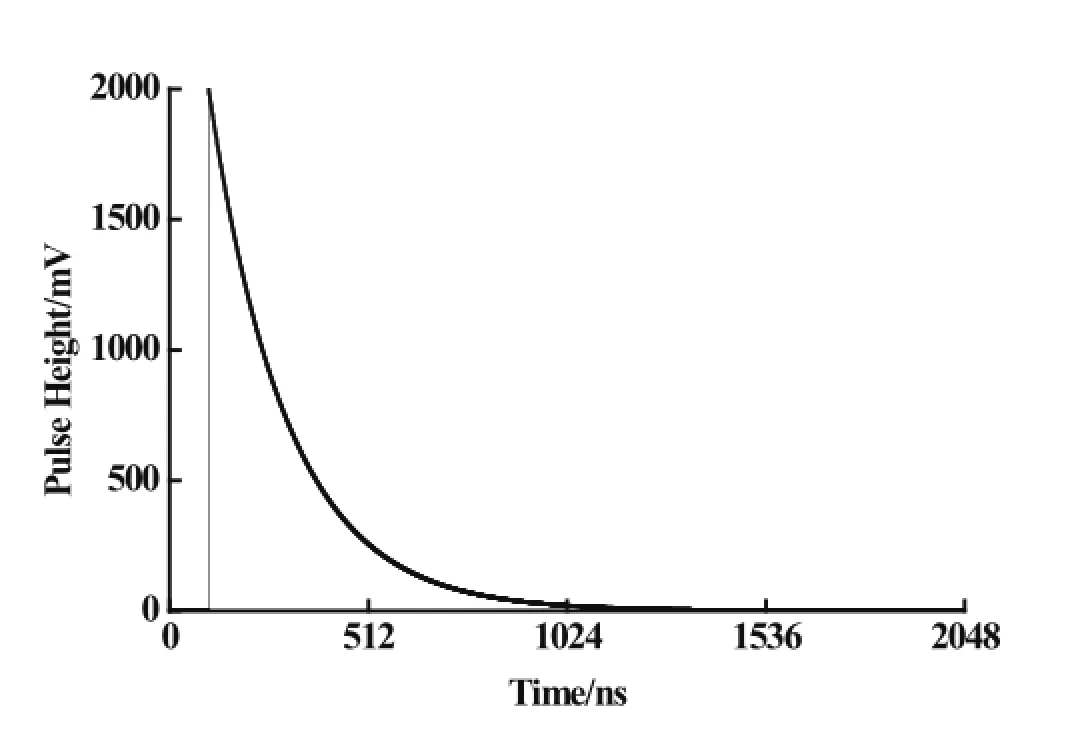
Fig.3.Simulations for a standard negative exponential signal.
2.Digital C-R shaping for a standard negative exponential signal.A C-R shaping circuit is inserted in Fig.4.The numerical recursive root of the C-R shaping circuit can be obtained based on the same analysis method in Section III and its recursive model can be written aswherek=Δt/(R·C).Fig.4 shows the input and output signals,at shaping parameterk=0.01,with Δt= 50ns.The input signal is the same as Fig.3 showing. Simulated results show that the standard negative exponential signal exists undershoot after C-R differentiator.
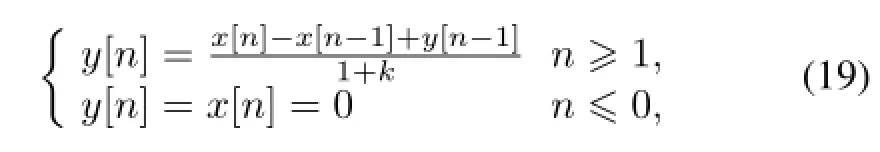
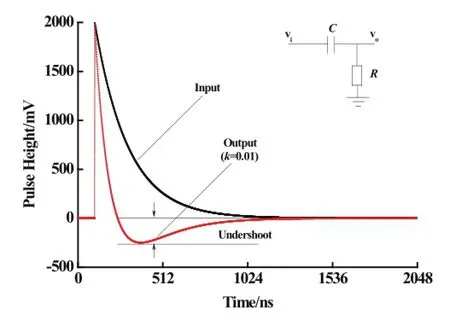
Fig.4.(Color online)Simulations for a standard negative exponential signal with C-R shaping.
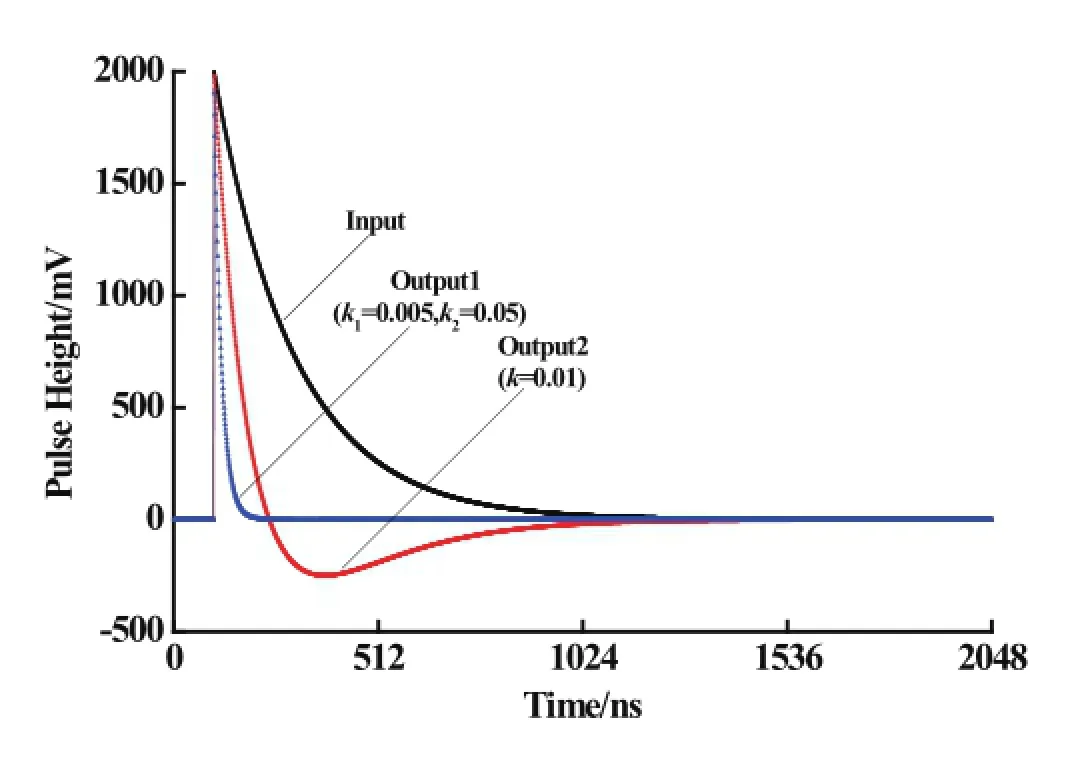
Fig.5.(Color online)Simulations for a standard negative exponential signal with the recursive PZC model.
3.Recursive model processing for negative exponential signal.A standard negative exponential signal the same as Fig.3 showing is used to test the recursive PZC model and an output signal with C-R shaping model presented in Fig.4 is used as a contrast.Fig.5 shows the input and output signals,at shaping parametersk1=0.005,k2=0.05 according to PZC condition.Output 1 looks like the output of real PZC circuit whereRPZ=10kΩ,R=1kΩ,C=1nf and Δt=50ns.The simulated results suggest that the recursive model for PZC circuit can eliminate undershoot,which exhibits in C-R shaping,and reduce the time constant of input signal.
4.Recursive model processing for nuclear signal.A twocomponent exponential signal can be described as
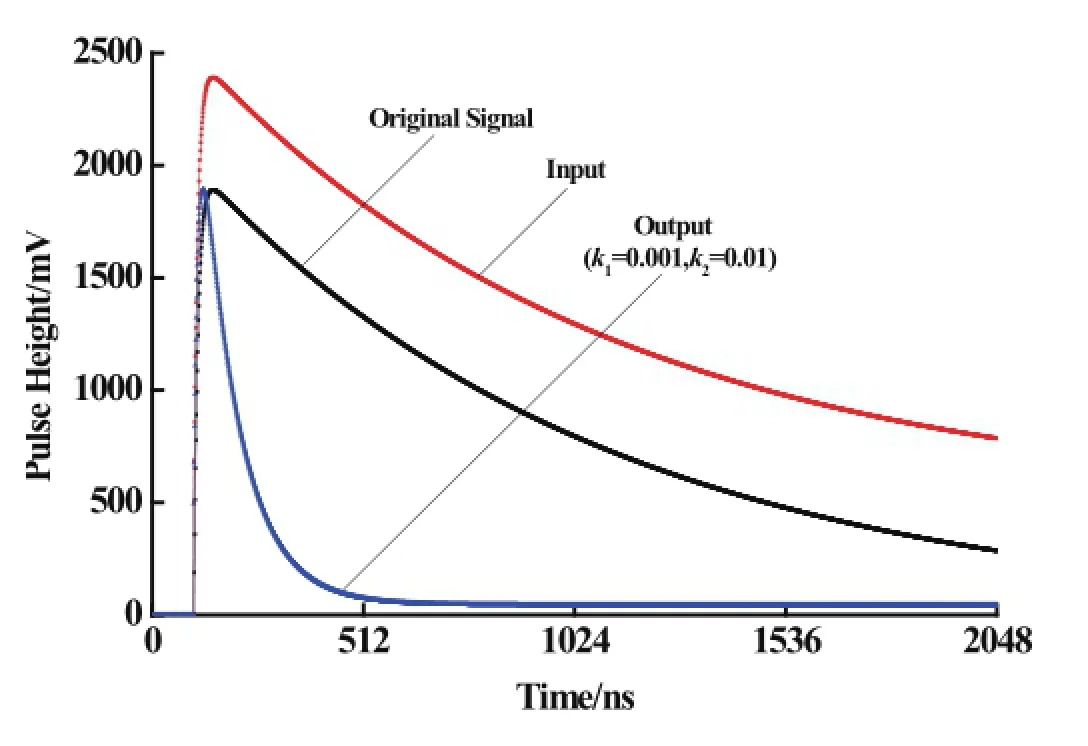
Fig.6.(Color online)Simulations for a two-component exponential signal with the recursive PZC model.
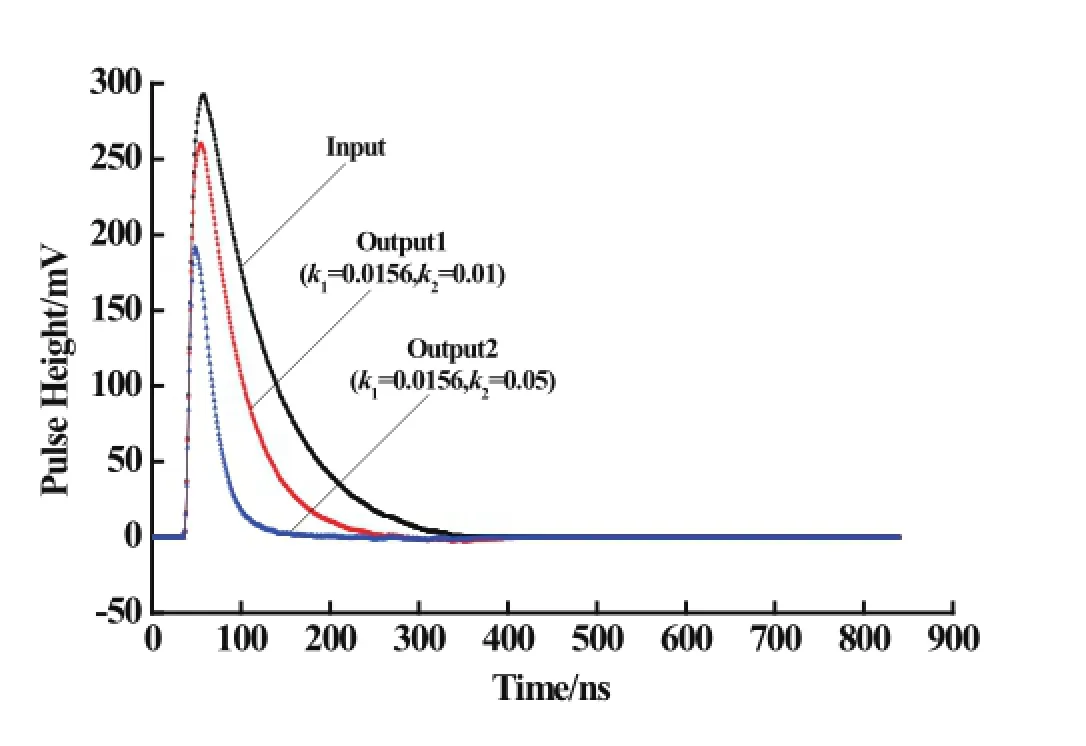
Fig.7.(Color online)Real data with the recursive PZC model.
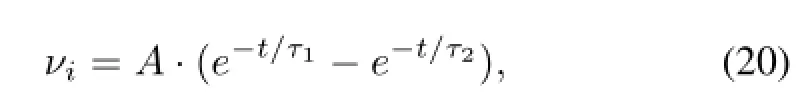
whereArepresents the amplitude of the two-component exponential signal,τ1is the decay constant before CSA, andτ2is the decay constant of CSA.A two-component exponential signal withA=−2000,τ1=10,τ2= 1000,which implies that the time constant of CSA is 50µsasΔt=50ns,issimulated as anoriginalsignal.A baseline is added to the original signal to simulate input signal.k1is set to 0.001 according to the cancellation requirement.
As shown in Fig.6,the difference of amplitude between original signal and output signal is small and the width of original signal is reduced without undershoot.A real x-ray signal test is done to test the recursive model.In this experiment,the input pulse was obtained from a SDD X-ray detector(Amptek).This pulse signal was sampled by a 10-bit ADC at 20MHz sampling rate,after a CSA preamplif i er and a C-R shaping circuit.The digital output of the ADC was transmitted to the PC forimplementation of the recursive model for PZC circuit. The time constant of the input signal is 3.2µs,thus the value ofk1is set to 0.0156.The results of this model for real data at different shaping parameters are given in Fig.7.It can be seen that the width of the real x-ray signal is reduced and the undershoot is eliminated.
IV.CONCLUSION
In this paper,a numerical recursive solution of PZC circuit is obtained through numerical analysis method in time domain and the recursive model of the circuit is also established.The accuracy of the model is verif i ed theoretically on KCL.The recursive model is tested on a computer simulation platform by using a standard negative exponential signal as input.Furthermore,a real x-ray signal is also processed by this recursive model.Simulation and test results show that it is easier to establish a recursive PZC model by using numerical analysis method to overcome the def i ciency of losing the time-domain characteristics in Laplace domain.The recursive PZC model supplies the contents of digital S-K f i lter[13]and enriches the methods of nuclear signal analysis,it can be used in real-time signal processing for preamplif i er signal,as well as for the digital pulse shaping analysis,which is one of the key techniques in digital nuclear instruments.
[1]WangZY,LouBQ,ZhuJJ,etal.PrincipleofNuclearElectronics.Beijing:Atomic Energy Press,1989,34–35(in Chinese).
[2]Xiao W Y,Wei Y X,Ai X Y,et al.Nucl Tech,2005,28:787–790(in Chinese).
[3]Li D C,Yang L,Tian Y,et al.Nucl Electr Detec Tech,2008,28: 563–566(in Chinese).
[4]Grybos P,Idzik M,Swientek K,et al.IEEE Int Symp Circ S, Kos,Greece,May 2006,1997–2000.
[5]Grybos P.2006 IEEE Nuclear Science Symposium,San Diego, United States,October 2006,226–230.
[6]Grybos P,Maj P,Szczygiel R.14thInternational Conference“Mixed Design of Integrated Circuits and Systems”,MIXDES 2007,Ciechocinek,Poland,June 2007,243–246.
[7]Grybos P and Szczygiel R.IEEE Trans Nucl Sci,2008,55:583–590.
[8]Seino T,Takahashi I,Ishitsu T,et al.Nucl Instrum Meth A, 2012,675:133–138.
[9]Liu S X,Zhang Y M,Yin Z J,et al.Nucl Tech,2005,28:783–786(in Chinese).
[10]Molodtsov S L and Gurbich A F.Nucl Instrum Meth B,2009,267:3484–3487.
[11]Gehrke R J and Davidson J R.Appl Radiat Isotopes,2005,62: 479–499.
[12]Wang J J,Fan T M,Qian Y G.Nucl Electr.Beijing:Atomic Energy Press,1983,151–158(in Chinese).
[13]Zhou J B,Zhou W,Lei J R,et al.Nucl Sci Tech,2012,23:150–155.
[14]Zhou J B,Zhou W,Fang F,et al.IEEE 2011 10thInternational Conference on Electronic Measurement and Instruments, Chengdu,China,August 2011,4:163–165.
10.13538/j.1001-8042/nst.25.010403
(Received July 5,2013;accepted in revised form January 15,2014;published online February 20,2014)
∗Supported by National High Technology Research and Development Program of China(863 Program)(No 2012AA061804-03)
†Corresponding author,hongxucdut@163.com
猜你喜欢
杂志排行
Nuclear Science and Techniques的其它文章
- Using activation method to measure neutron spectrum in an irradiation chamber of a research reactor∗
- A neural network to predict reactor core behaviors∗
- Research on GPU-accelerated algorithm in 3D f i nite difference neutron diffusion calculation method∗
- Development of a three dimension multi-physics code for molten salt fast reactor∗
- Performance simulation and structure design of Binode CdZnTe gamma-ray detector
- Effectiveness and failure modes of error correcting code in industrial 65 nm CMOS SRAMs exposed to heavy ions∗
