混合陶瓷滚子导轨副的研究
2014-04-23李宇鹏刘来超罗水新
李宇鹏 刘来超 罗水新
(①燕山大学,河北 秦皇岛 066004;②北京机床研究所,北京 101312)
作为某些精密数控机床的重要功能部件,滚动导轨副的性能会对机床的性能、加工精度产生很大的影响。钢制滚子导轨副工作过程中存在噪声较高、抗振性较弱、对温升敏感、精度保持性较差等不足,工业陶瓷与轴承钢相比具有弹性模量大、硬度高、热膨胀系数小、内阻尼大、耐磨性好等优点。将陶瓷材料用于滚动导轨副不仅可继承金属滚动导轨副的许多优点,而且能带来诸多新优势,也能拓展滚动导轨副的应用范围。因此,对混合陶瓷滚子滚动导轨副的研究,对提高和拓展滚动导轨副的性能,从而提高机床的性能具有重要意义。
本文在初步确定滚子母线为直母线的前提下,针对直母线滚子导轨副存在边缘效应、润滑条件差、精度寿命短等缺点,设计了一种新型陶瓷滚子,并进行了凸度参数优化,在此基础上进行空心结构滚子设计,然后对混合陶瓷滚子导轨副进行动态特性分析,为这种新型滚动轴承的综合性能优化奠定了基础。
1 混合陶瓷滚子导轨结构
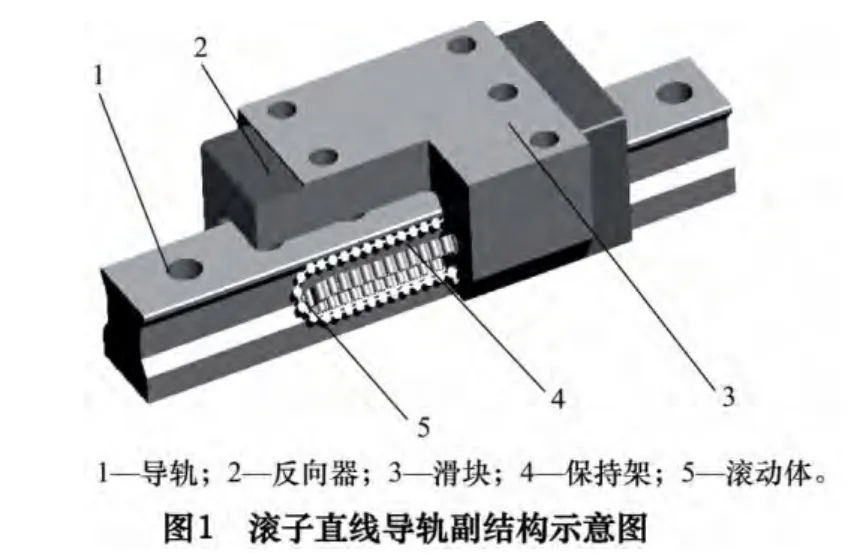
混合陶瓷滚子直线导轨结构如图1 所示,由支承导轨1,反向器2,滑块3,保持架4,陶瓷滚子5 构成,每列滚子数24,导轨副额定载荷300 kN。该导轨副支承导轨总长1 000 mm、宽50 mm,高50 mm,滑块总长100 mm,宽97 mm,高71 mm,滑块在导轨上居中布置。
2 滚子的结构及参数优化
2.1 基于等强度理论的滚子凸度参数优化[1]
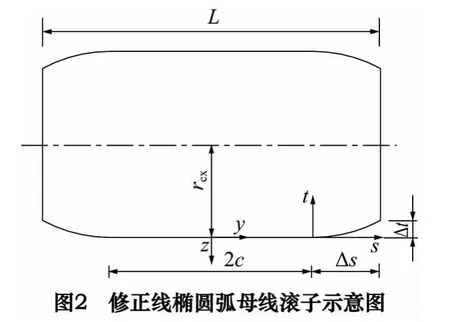
研究表明[2-4],滚子的母线形状对其接触疲劳寿命和接触应力沿滚子长度方向分布的均匀性有着决定性的影响,合理设计滚子的母线可以改善导轨接触区摩擦、磨损的均匀性,有利于形成弹性流体动力润滑,降低导轨工作的振动和噪音,对提高导轨的精度和寿命有关键作用。本课题研究了一种新凸型滚子——修正线椭圆弧母线滚子,如图2 所示。采用T-LHorng[5-6]变形理论和等强度设计理论对滚子的凸度量进行优化[1],优化后的滚子尺寸参数为:L=7.6 mm,rcx=3 mm,Δt=3 μm,Δs=0.6 mm,c=3.2 mm。经一系列计算、分析比较得知,采用该母线滚子的接触刚度、承载力均高于其他母线的滚子,接触应力分布均匀性显著提高,有利于提升导轨的耐磨性。
2.2 凸度滚子空心度参数优化[1]
为提升混合陶瓷滚子导轨的抗振性、冷却及润滑条件、抑制热畸变能力、微动灵敏度等性能,以滚子内径为设计变量,以滚子等效变形量为状态变量,滚子体积为目标函数,在前述确定的凸型及凸度参数条件下,对滚子进行空心度优化设计,其结果如图3~5 所示。
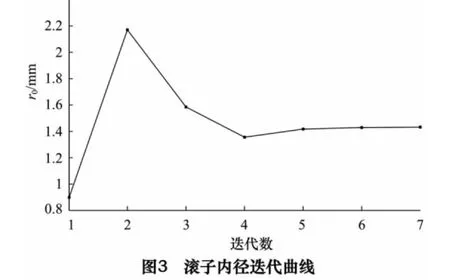
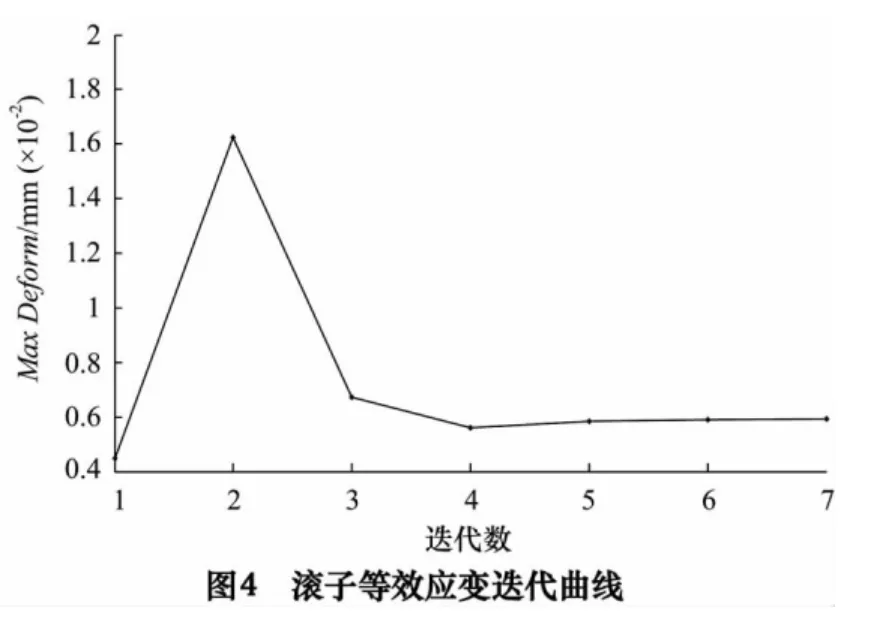
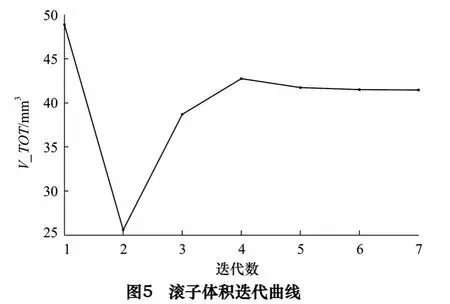
优化后滚子体积由53.715 mm3减至41.471 mm3,滚子质量降低22.8%。滚子空心内的介质改善了导轨的润滑、温升及热畸变等状况,能提升导轨精度保持性。空心滚子的“弹簧性”和空心内介质的综合作用,能提高导轨的吸振及抑制噪声的能力。滚子质量和惯性的减小使导轨的运动响应更灵敏、防爬能力更佳、能耗更低,可提升导轨的精度。空心滚子也可减小其回程区滚道的破坏几率。因此,空心陶瓷滚子导轨副更适用于某些精密或超精密机床。当然,要完善空心滚子导轨副尚有许多工作要做,对空心滚子的制造精度也需进一步探讨。
3 导轨副动态特性分析
为研究混合陶瓷滚子导轨副的动态特性,先要对其进行谐响应分析。谐响应分析采用弹簧-阻尼单元模拟导轨副的结合面,导轨副约束后的有限元模型如图6所示,为避免模型共振时出现响应无穷大情况,谐响应分析之前还需设定弹簧阻尼系数或系统的阻尼比。

3.1 导轨副的阻尼比
混合陶瓷滚子导轨副的阻尼产生源主要涉及滚动摩擦阻尼及结构内摩擦阻尼,通常将模型的阻尼设定为粘滞性阻尼。由于典型结构体系的真实阻尼特性复杂、难确定,一般采用自由振动条件下具有相同衰减率的等效粘滞阻尼比ξ 近似表示实际结构阻尼。依据文献[7],本课题用有限元法研究模型在既定冲击载荷作用下的动态响应来确定模型的阻尼比,对比研究自增韧氮化硅陶瓷空心滚子和Gcr15 金属实心滚子在矩形脉冲作用下冲击响应的振动自由衰减,通过获取对数衰减振动第i 个振幅与第i+n 个振幅之比来获得整体模型的阻尼比。
(1)结构动力学分析
为获得滚子的自由衰减特性曲线,对上述模型施加一矩形脉冲,用脉冲函数表示该冲击载荷为
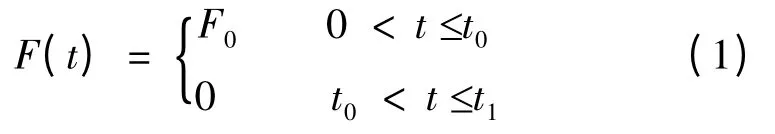
将式(1)表达的外载荷以节点载荷形式均匀施加在滑块上表面,施加的载荷大小F0设为C0,数值为
252 kN,瞬态分析采用完全法。
(2)冲击动力响应特点
取t0=0.05 s,t1=0.1 s。分析该模型的位移自由衰减部分曲线,即模型卸载后的时域响应信号,对滑块对称面最中间节点的位移进行分析。由于在不同滚子结构下导轨的冲击响应特点相似,故只给出自增韧氮化硅陶瓷空心滚子的情况,取导轨和滑块的弹性模量Ex=2.07 ×105MPa,泊松比0.3,滚子弹性模量3.1 ×105MPa,泊松比0.27。图7 为在陶瓷空心滚子条件下滑块上对称面中心点uy位移的时域信号,经过一个绕平衡位置的衰减振动,加载及卸载都将趋于一个稳定值,加载时,uy趋于稳定值-0.015 27mm,卸载时,uy趋于稳定值-7.688 ×10-11mm,其近似为0,这与实际情况相符。
(3)阻尼比ξ 的求取

依据上述分析及混合陶瓷滚子导轨副为低阻尼体系的特点,利用卸载后导轨系统自由衰减的特性,考察任意两个分别在n(2π/ωD)和(n+1)(2π/ωD)时刻出现的相邻正波峰An和An+1,可得相邻波峰值的比为[8]
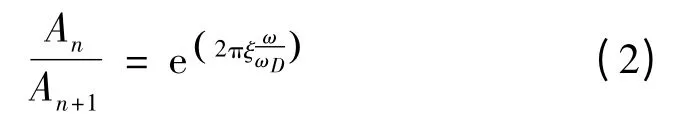
两边取自然对数并代入ωD=ω·sqrt(1 -ξ2),可得对数衰减率δ 为
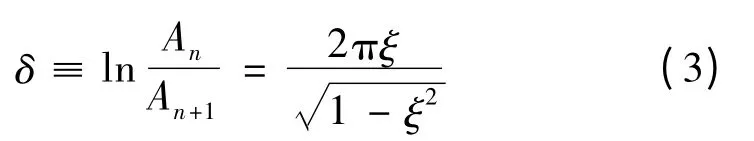
对小阻尼情况,上式可近似为

对低阻尼体系,取相隔m 周的衰减波峰来计算阻尼比,可获得较高精度,即
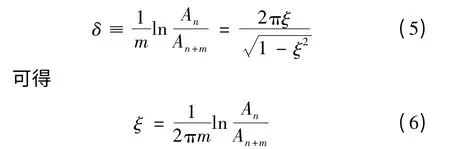
陶瓷滚子与金属滚子条件下,将相隔6 周取的10个幅频值大小代入式(5)分别进行计算,最后可得陶瓷空心滚子条件下滚动直线导轨副的阻尼比ξ=0.038 9,实心金属滚子条件下滚动直线导轨副的阻尼比ξ=0.022 4。
3.2 谐响应分析
求取了阻尼比之后,通过命令DMPRAT 输入模型的阻尼比。根据滚动直线导轨副工作的实际情况,施加载荷条件为:滑块4 个端点上分别施加一个幅值为0.1Cr,即大小为2 520 N,方向为-y 向、相位为零的载荷,同时在滑块一端的两个端点上施加一个大小为1 260 N,方向为z 向的载荷,激振频率范围是200~2 000 Hz,分90 个载荷步,载荷形式为阶跃载荷,使载荷的幅值保持相等。考察滑块上表面中心节点及滑块两侧中间节点的振幅,取值点如图8 所示,空心陶瓷滚子分析时导轨副的切向刚度k1=24.1 N/μm,法向刚度k2=1.6 N/μm,实心金属滚子分析时导轨副的切向刚度k1=2.3 N/μm,法向刚度k2=1.7 N/μm。
(1)陶瓷空心滚子情况
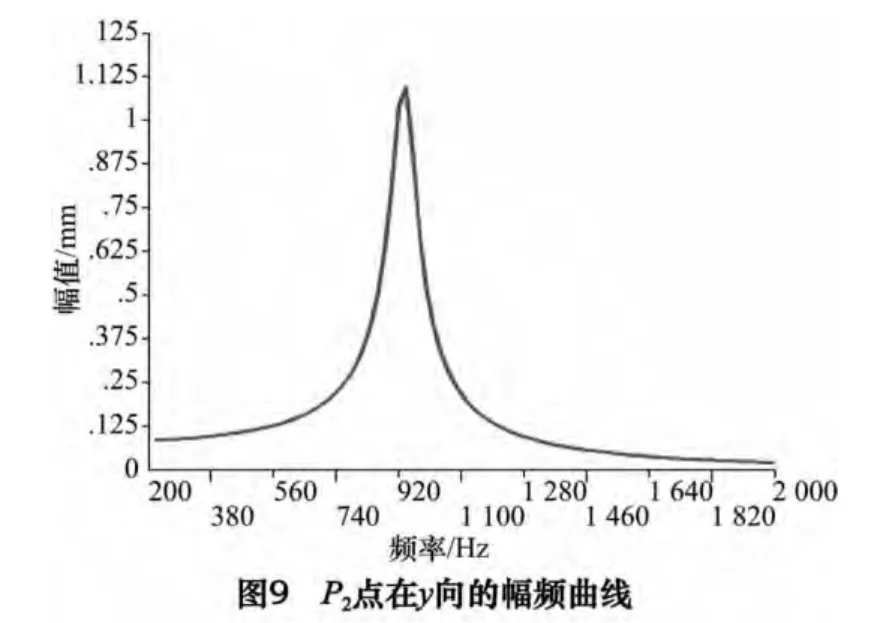
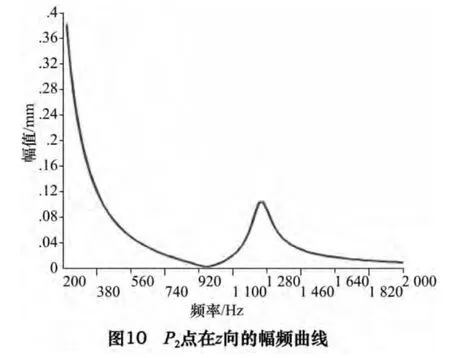
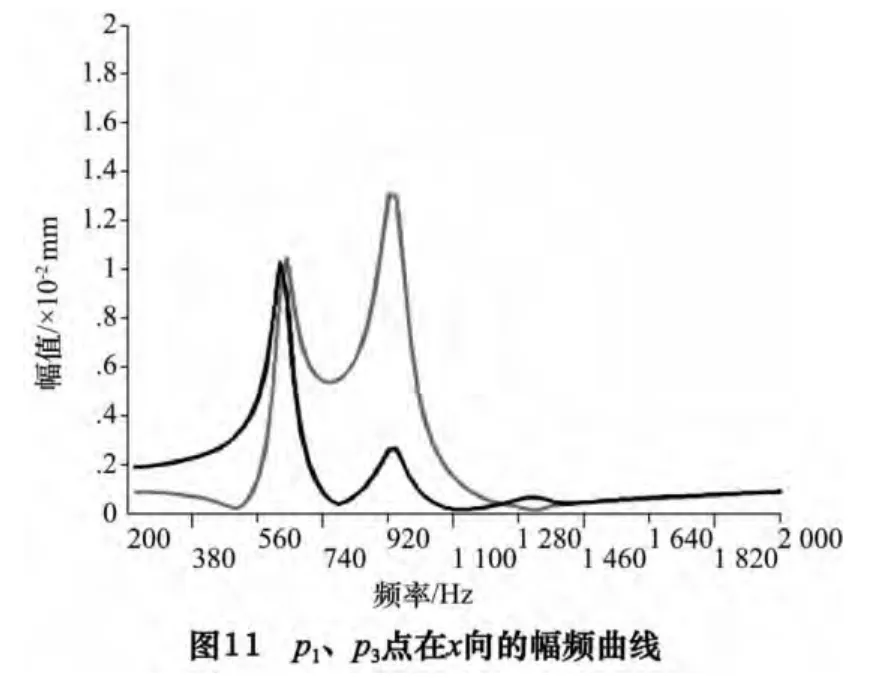
考察p2点y 向及z 向振幅及p1、p3两点的x 向振幅。P2点y 向及z 向的幅频曲线如图9、10 所示,模型在y 向的共振频率发生在940 Hz,幅值大小为1.094 mm,在z 向除去刚体振型外,共振频率发生在1 260 Hz,幅值为0.104 mm,p1、p3在x 向的幅频曲线如图11 所示,p1点在x 向的共振频率发生在640 Hz 及920 Hz,幅值大小分别为0.010 4 mm 及0.013 mm。p3点在x 向的共振频率发生在620 Hz 及940 Hz,幅值大小分别为0.010 3 mm 及0.002 68 mm。
(2)实心金属滚子情况
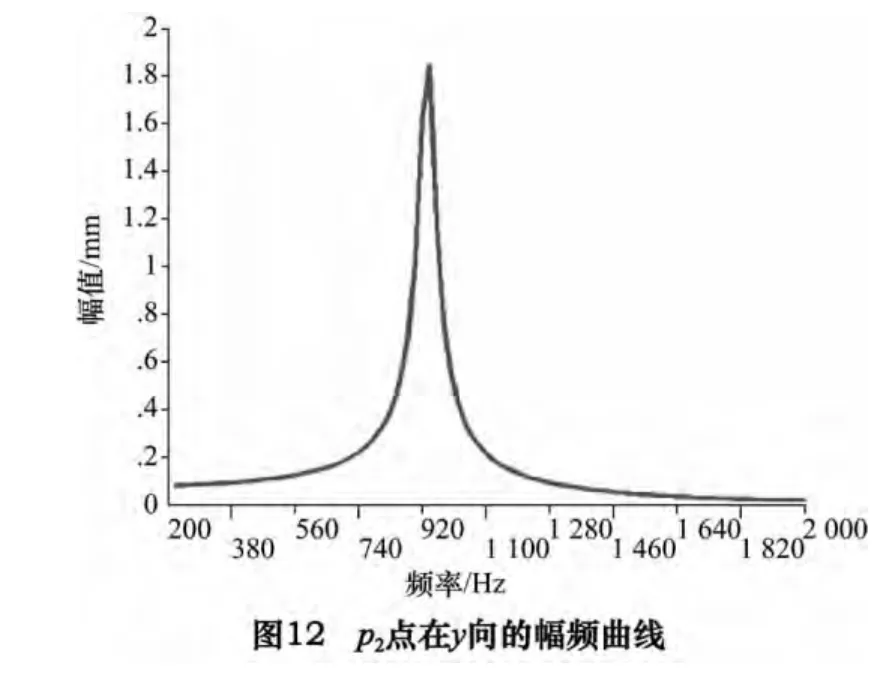
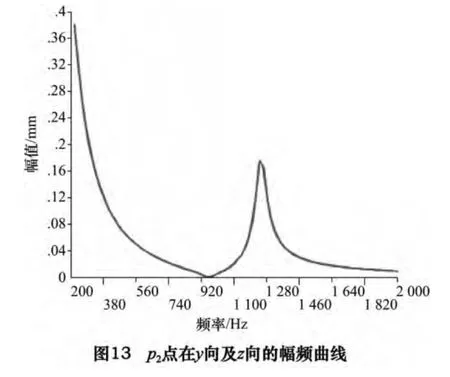
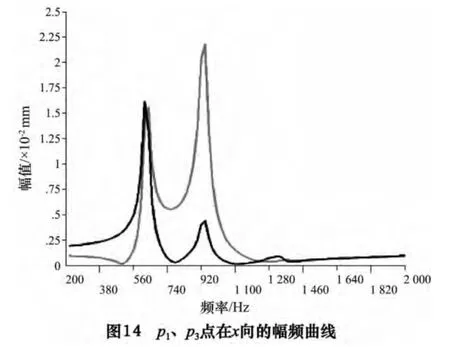
P2点y 向及z 向的幅频曲线如图12、13 所示,由这两图可知,模型在y 向的共振频率发生在940 Hz,幅值大小为1.844 mm,z 向的共振频率发生在1 240 Hz,幅值大小为0.175 mm,p1、p3在x 向的幅频曲线如图14 所示,p1点在x 向的共振频率发生在640 Hz 及940 Hz,幅值大小分别为0.015 5 mm 及0.021 7 mm。p3点在x 向的共振频率发生在620 Hz 及940 Hz,幅值大小分别为0.016 mm 及0.004 28 mm。
(3)结果对比分析
由图9~14 可知,自增韧氮化硅空心凸度滚子导轨副在各个方向的振幅值均小于Gcr15 滚子导轨副。其中y 向的幅值下降率为40.7%,z 向的幅值下降率为40.6%,p1点在x 向的幅值下降率分别为32.9%和40.1%,p3点在x 向的幅值下降率分别为35.6% 和37.4%,在误差允许范围内,可认为幅值下降比率基本相等。这表明混合陶瓷滚子导轨副具有四方向等刚度的特性,具有比金属滚子导轨更好的抗振性。
4 结语
提出研发混合陶瓷滚子导轨副的必要性与可行性,并作了一些基础性前期研究工作:
(1)研究、设计出新型凸度陶瓷滚子,并对凸度参数进行了优化,在此基础上进行了凸度陶瓷滚子空心结构的优化设计。
(2)研究结果表明陶瓷滚子与钢制滚子相比所具有一些优势,空心陶瓷滚子与实心陶瓷滚子相比所具有一些优势。
(3)对新型结构的混合陶瓷滚子导轨副的抗振性进行了理论研究和对比性的验证分析,结果表明混合陶瓷滚子导轨副相对于同规格的金属滚子导轨副抗振性提升约40%。
[1]罗水新.混合陶瓷直线型滚柱导轨副的研究与设计[D].秦皇岛:燕山大学,2013.
[2]马家驹.线接触副凸度设计的研究_凸度设计[C].武汉:第五届全国摩擦学学术会议,1992:175 -179.
[3]徐浩,汤勇,王大力.圆锥滚子轴承凸度设计[J].轴承,2003(9):6-7.
[4]刘彦奎,沈卫,魏延刚.滚动体素线形状对圆柱滚子轴承应力的影响[J].轴承,2007(3):1 -3.
[5]Horng T L,Ju S H.Stiffness of arbitrarily crowned roller compressed between two plate[J].Proceedings of the Institution of Mechanical Engineers Part J-Joumal of Engineering Tribology,2003,217:375-384.
[6]Horng T L,Ju S H.A deformmion formula for circular crowned rollers compressed between two plates[J].Journal of Tribology-Transactions of the ASME,2000,122:405 -411.
[7]李健伟,潘存云,王荣吉,等.实心和空心滚子结构阻尼的动态特性[J].振动与冲击,2009,28(12):43 -46.
[8]R.克拉夫,J.彭津.结构动力学[M].2 版.北京:高等教育出版社,2006.
