高速陶瓷电主轴动力学特性研究*
2014-04-23邱海飞
邱海飞
(西京学院机电技术系,陕西 西安 710123)
高速数控机床是装备制造业的技术基础,电主轴作为高速加工系统的核心部件,对于数控机床的产品质量、切削精度、生产效率及运行稳定性等都有重要影响[1]。随着现代化制造技术朝着高速化、智能化及大功率化方向发展,数控机床对电主轴提出了更高的性能要求。当前市场上标准型机床转速已达30 000~40 000 r/min,日本精工已成功研制出了50 000 r/min的超高速机床用电主轴。为了更好地适应数控加工系统高刚度及快速爬升等特点,一些高性能工程陶瓷材料被越来越多地应用于电主轴的设计与制造。相对于传统材质,陶瓷材料能够有效解决影响电主轴研发水平的关键技术,对于电主轴的技术改造和性能提升具有重要的应用价值。目前,国内洛阳轴研科技股份有限公司、沈阳建筑大学在陶瓷电主轴研究方面取得了一定成果,国外瑞士IBAG 公司、德国GMN 公司、美国Ingersoll 公司及日本FANUC 公司等在新型高速电主轴的研究与探索方面处于领先地位[2]。
随着材料科学和成型工艺的快速发展,陶瓷电主轴的设计与制造将会日益成熟,必将成为未来电主轴发展的主流方向。本文将陶瓷材料Si3N4应用于高速铣削电主轴,在等效力学模型基础上对其动力学特性展开深入研究,并通过参数化设计实现了主轴结构的动力学优化,为陶瓷电主轴的结构改进及高速化设计提供了技术支持。
1 工程陶瓷材料
陶瓷属于无机非金属材料,相对于一般工程材料,陶瓷材料具有许多优异性能。由于质量密度较小,采用工程陶瓷制成的旋转部件可有效减轻结构自重和离心力,有利于转子系统的高速化运行。陶瓷材料具有很高的弹性模量和抗剪切应力,同时具有很低的抗拉伸应力,能够大幅提高零部件的结构刚度、抗疲劳强度及工作寿命;此外,陶瓷材料热膨胀系数小、耐高温、加工尺寸稳定,避免了热处理引起的变形、相变等问题。常见陶瓷材料的性能参数见表1,氮化硅、碳化硅、氧化铝及氧化锆等是目前最常用的工程陶瓷[2]。由于陶瓷材料自身优良的机械物理综合性能,使其在众多工程领域具有广阔的应用和开发前景,目前已被广泛应用于航空航天、机械、电子、军事、化工以及精密制造等领域。
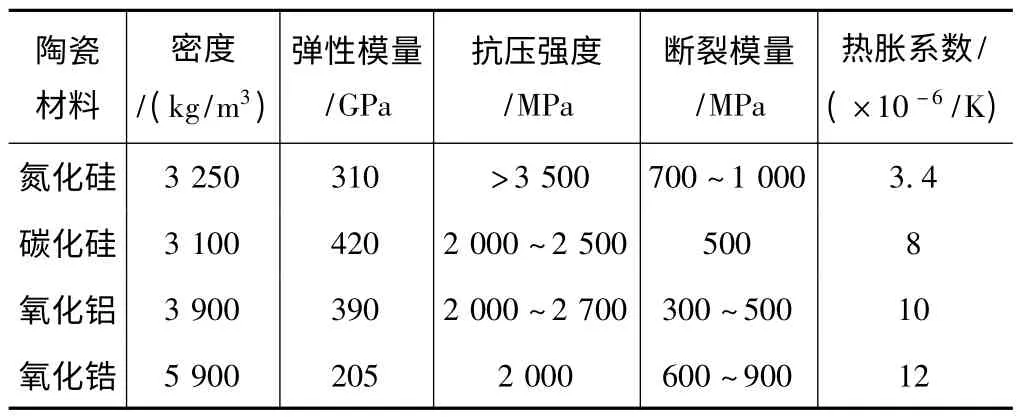
表1 常见陶瓷材料性能参数
2 等效力学模型
作为数控机床的核心部件,电主轴具有质量轻、惯性小、响应快、振动及噪声小等优点。为了保证良好的动力学性能和稳定性,电主轴多被设计为独立单元配置于各类数控机床。高速电主轴属于典型的智能化功能部件,一般由主轴、轴承、动力源、机架4 部分构成[3]。为了便于建模、计算及分析,对某型铣床用电主轴部件进行结构简化,创建其等效力学模型。如图1 所示,将主轴段等效为弹性梁单元,并对其赋予不同截面属性,通过节点将各梁段联接为一体;采用弹簧-阻尼单元模拟轴承支撑,其中,主轴前端装配4 组滚动球轴承1、2、3、4,各轴承间距均为d1=54 mm,主轴后端装配一个圆柱滚子轴承5,轴承4 与轴承5 之间距离d2=223 mm;将主轴上的质量元件等效为集中质量点,分别为前端盖-M1、圆螺母1 -M2、后端盖-M3、带轮-M4、圆螺母2 -M5。
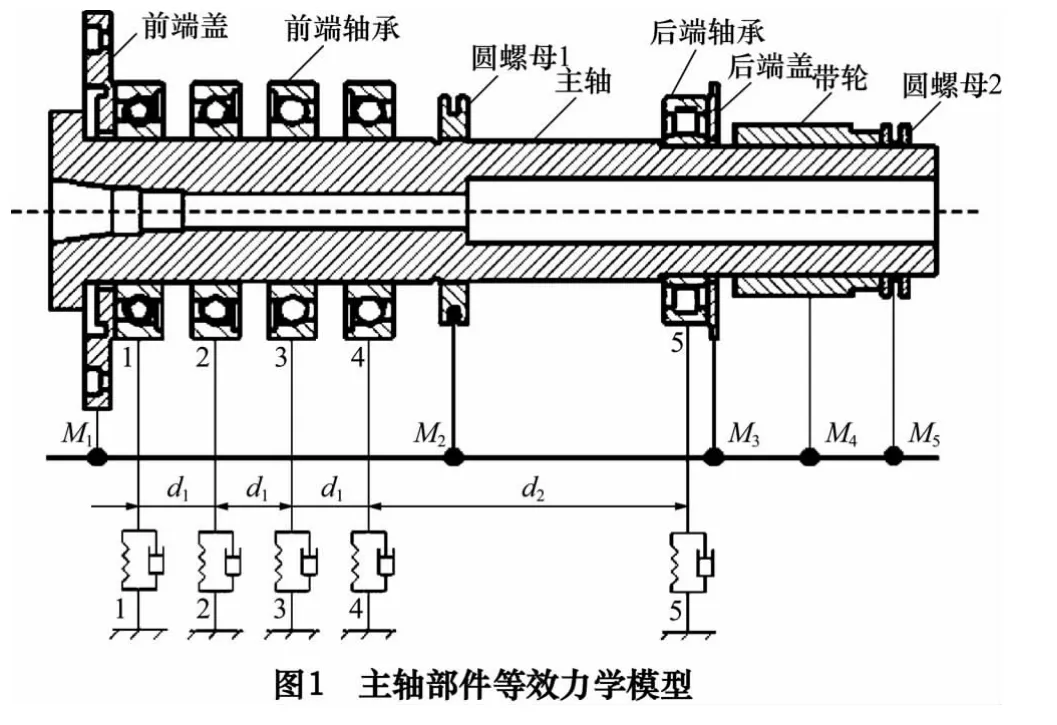
3 动力学建模
3.1 理论依据
电主轴为典型高速旋转部件,由等效力学模型可知,主轴段上装配有5 个集中质量M1、M2、M3、M4、M5,机床工作时这些集中质量随主轴一起高速旋转。根据转子动力学理论,对于包含多个质量元件的转子系统,其横向振动微分方程如式(1)、式(2),其中,M 为对角矩阵,其对角线元素由集中质量m 和直径转动惯量Jd组成;J 为转动惯量矩阵,是以极转动惯量Jp为对角线元素的对角矩阵;K 为刚度矩阵,是以刚度系数k 为元素的对称矩阵;ξ1、ξ2为位移向量;ω 为转子系统角速度[4]。
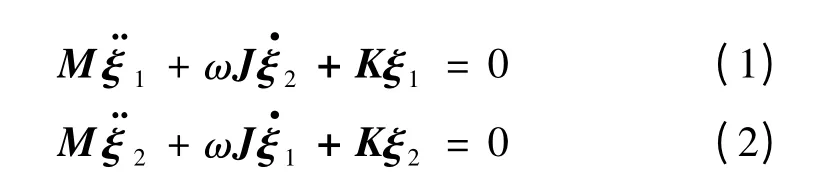
对于集中质量M1、M2、M3、M4、M5,主轴作横向振动时可由4 个方向矢量表征其空间位移,分别为线性位移x、y 和角位移θx、θy,故可通过20 个位移矢量来确定主轴横向振动位移。如式(3)、式(4)所示,ξ1、ξ2均为10 维列向量,则由矩阵与向量乘积关系可知,M、J、K 应为10 阶方阵。
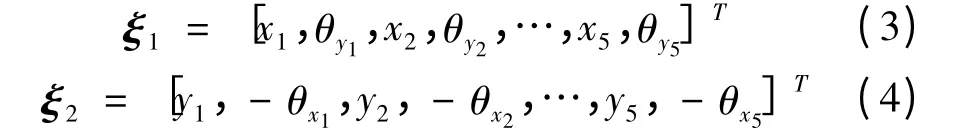
3.2 参数化有限元模型
通过弹簧-阻尼单元COMBIN14 模拟轴承支撑,如图2 所示。COMBIN14 单元不计质量,且不考虑弯曲和轴向载荷,模拟轴承支撑时为纵向弹簧-阻尼结构,每个节点包含x、y、z 这3 个自由度。如图3 所示,一个轴承可由4 个对称分布的COMBIN14 单元模拟,前端轴承刚度K1=272.6 MPa,阻尼Cv1=1 170 N·s/m,后端轴承刚度K2=201.3 MPa,阻尼Cv2=810 N·s/m[5]。陶瓷电主轴参数化有限元模型如图4 所示,根据主轴实际结构设置边界条件,将轴承自由端支撑节点S1、S2、S3、S4完全约束,并限制前端轴承内部支撑节点S1、S2、S3、S4轴向位移,后端轴承为可浮动支撑,故不限制自由度。
4 动态分析
4.1 自振频率与振型
模态分析是结构动力学分析的基础,在此基础上可以进行谐响应分析、瞬态动力学分析及谱分析等。对相同结构的钢制电主轴与陶瓷电主轴进行自由模态分析,计算其低阶自振频率与振型。由表2 可知,Si3N4电主轴的1~5 阶自振频率均高于45 钢电主轴,说明陶瓷材料可以明显改进电主轴的动力学特性,相对于钢制主轴,陶瓷电主轴能够适应更高的工作转速。由图5 可知,陶瓷电主轴的1、2 阶振型表现为前后端的径向摆动,最大形变量分别出现在主轴后端和前端位置;3、4 阶振型主要表现为主轴径向弯曲变形,前端轴承支撑位置附近变形最为明显。如果外部干扰频率或主轴工作频率与某一阶自振频率接近或重合,主轴部件就会按照图5 所示振动模式发生剧烈振动(即共振),严重时甚至造成主轴结构断裂,所以数控机床的工作转速频率应尽量避开主轴系统的自振频率。
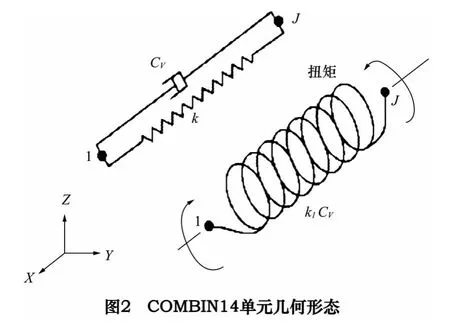
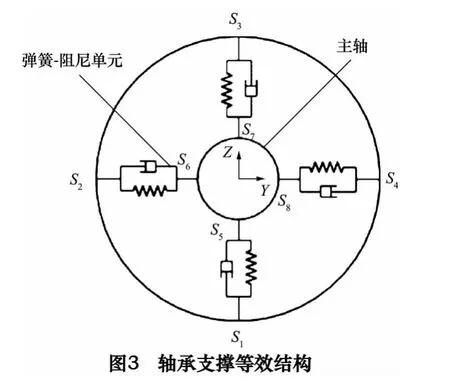
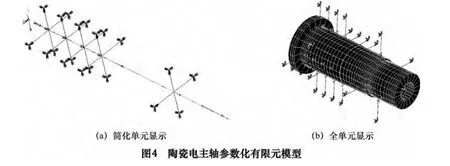
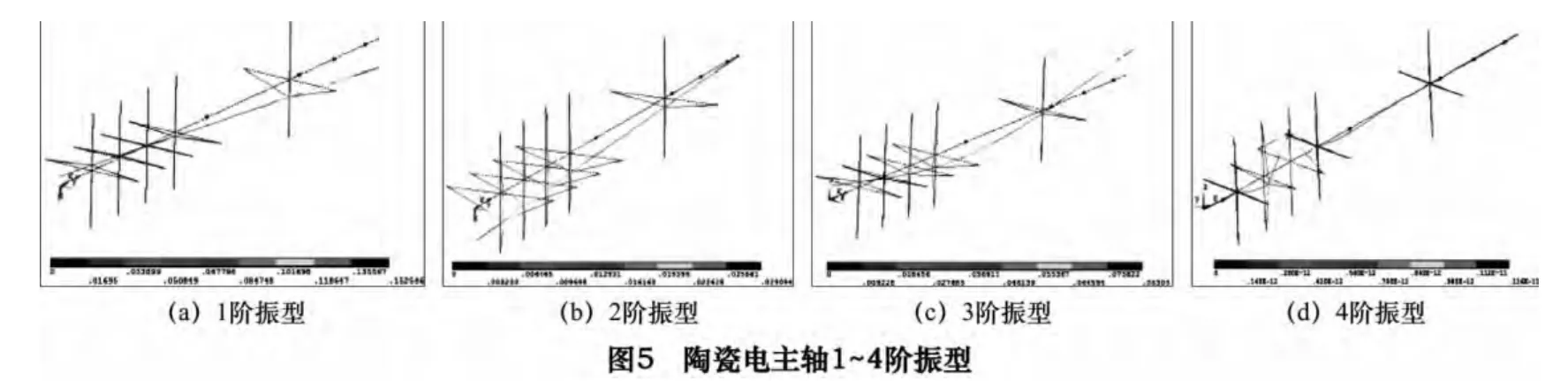
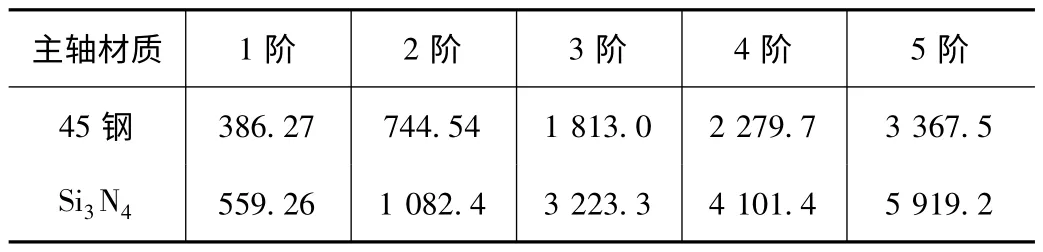
表2 钢制主轴与陶瓷主轴自振频率比较 Hz
4.2 临界转速
数控机床以临界转速工作时,主轴系统进入临界状态,此时主轴部件将会产生剧烈振动,不利于机床稳定运行,而当主轴在临界转速之外一定范围旋转时,主轴将趋于稳定运行。准确计算临界转速是主轴系统动平衡设计的前提,对于工况下数控机床的速度控制与调节具有重要参考价值。考虑陀螺效应,采用ANSYS 的动力缩减技术对陶瓷电主轴进行临界转速分析。静止坐标系中的转子运动微分方程如式(5),其中M 为质量矩阵、C 为阻尼矩阵、CGYR为陀螺矩阵、K 为刚度矩阵、δ为节点位移向量、F 为节点载荷向量。
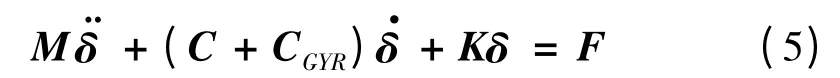
在0~40 000 r/min 范围内分析陶瓷电主轴的临界转速,通过OMAGA 命令对主轴系统施加不同转速,在此基础上对其进行模态分析,计算各阶自振频率及振型。根据振动理论,基频(第1 阶自振频率)是衡量结构动力学特性的重要指标,基频越大,结构的抗振性能就越强。表3 为不同转速下的主轴自振频率,分析可知,随着主轴转速的提高,其1 阶自振频率呈下降趋势,由此可见,高速状态下的主轴动力学特性会逐渐变差。
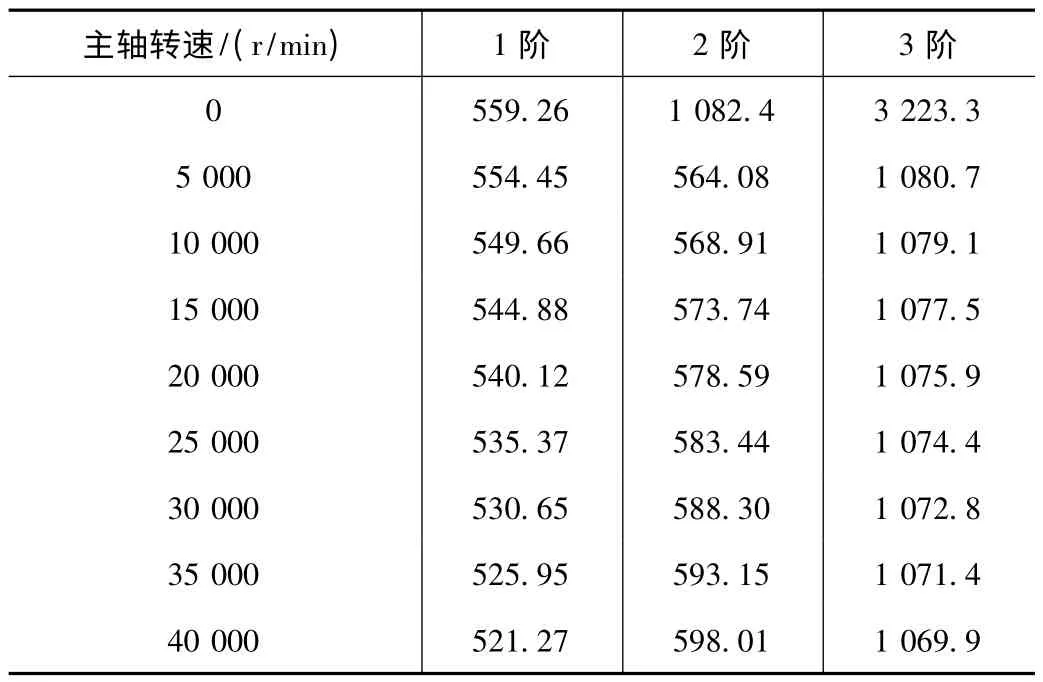
表3 不同转速下的主轴自振频率 Hz
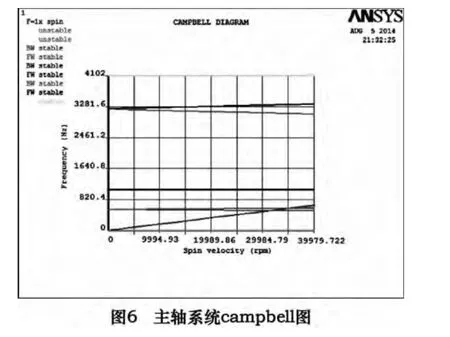
在模态分析基础上获得陶瓷电主轴的campbell图,如图6 所示,其横坐标为主轴转速,纵坐标为主轴系统自振频率[4]。由图6 可知,主轴系统的自振频率线与内部激振力线有两个交点,由此确定陶瓷电主轴在0~40 000 r/min 范围内包含两阶临界转速,分别为31 740 r/min(一阶)和35 627 r/min(二阶),与之对应的主轴系统共振频率为529 Hz 和593.78 Hz。另外,当工作转速达到一阶临界转速时,主轴系统发生反进动共振;当工作转速达到二阶临界转速时,主轴系统发生正进动共振。在一阶临界转速下对陶瓷电主轴进行模态分析,其第1 阶振型和与之对应的轴心轨迹如图7 所示,由图可知,主轴的1 阶振动模式主要表现为前后端的径向摆动变形,最大变形出现在后端位置;轴心轨迹也叫涡动轨迹,为一椭圆形运动轨迹,由轴心轨迹可判断主轴轴心线在某一自振频率下偏离平衡位置的幅度,为准确研判主轴动力学特性提供重要参考。
4.3 谐振响应
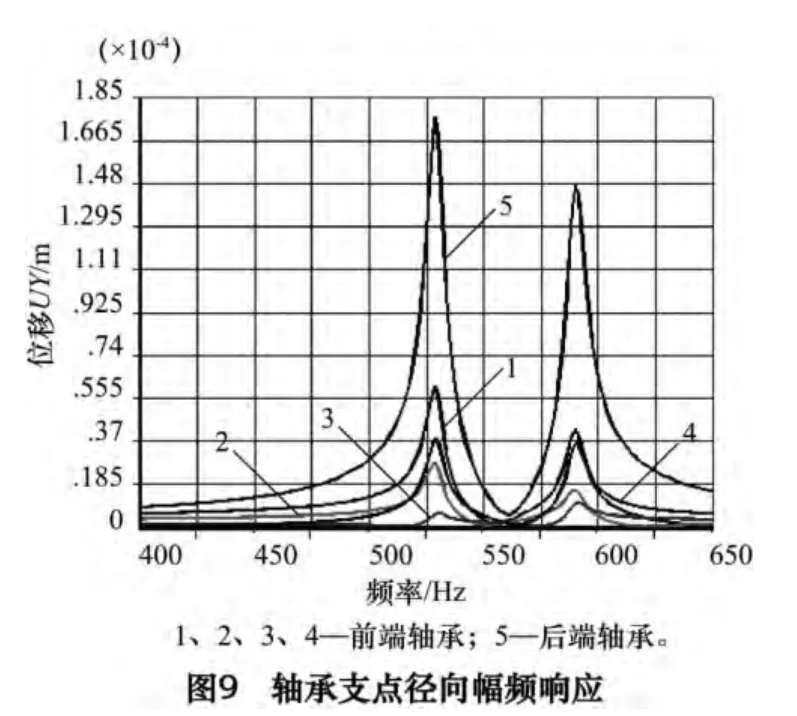
谐响应分析可以有效预测和评估结构的持续动力学特性,能够确定线性结构在已知频率范围内承受正弦(简谐)载荷作用时的稳态响应。根据实际工况,刀具切削工件过程中会对陶瓷电主轴产生周期性激振,当激振力与主轴自振频率接近或重合时就会发生共振,这对于机床的加工精度和稳定运行是极为不利的[5]。假设激振力P(t)随时间t 按照正弦规律变化,其表达式见式(6),其中p 为激振力幅值,N;ω 为强制频率,Hz;φ为相位,rad。将激振力幅值设为3 500 N,施加于主轴前端位置,方向与Y 轴负向一致;根据临界转速对应的共振频率,将强制频率范围定义为400~600 Hz,初始相位近似为0。采用完全法(Full 法)对陶瓷电主轴进行谐响应分析,计算过程划分为150 个子步。
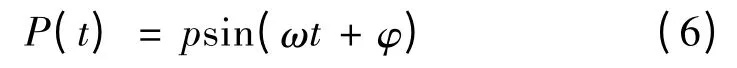
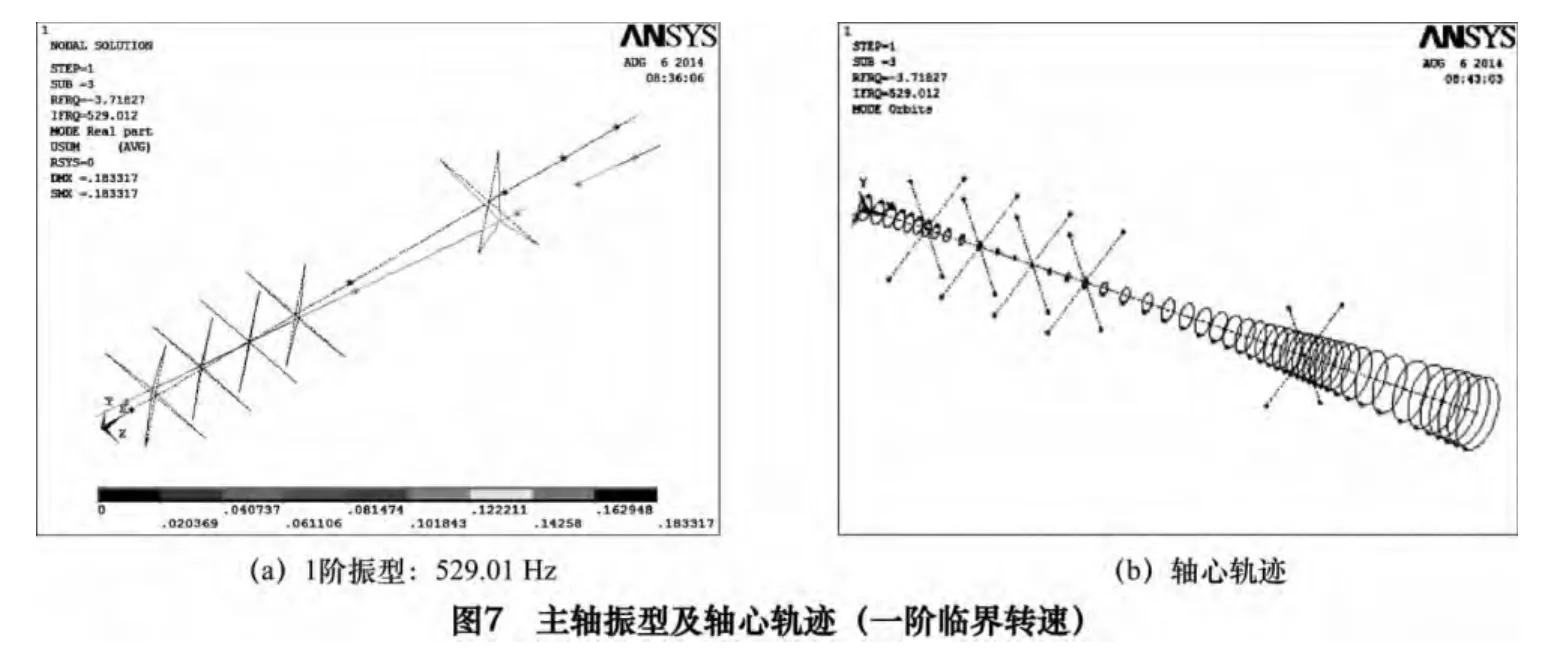
通过扫频计算获得陶瓷电主轴关键位置的位移-频率响应。由图8 可知,主轴前后端径向位移响应曲线存在两个峰值,分别位于528.75 Hz 和590 Hz 频率处,这与主轴系统一、二阶临界转速对应的共振频率基本一致,由此验证了临界转速计算的准确性。另外,在简谐激振载荷P(t)作用下,主轴前后端在共振频率处的径向位移最大,此时主轴动刚度最小、抵抗变形能力最弱。比较前后端位移响应曲线可知,主轴前端径向位移峰值(99.82 μm、71.94 μm)明显小于后端径向位移峰值(295.45 μm、241.62 μm),说明主轴前端动刚度大于后端动刚度,有利于提高切削精度和加工稳定性。
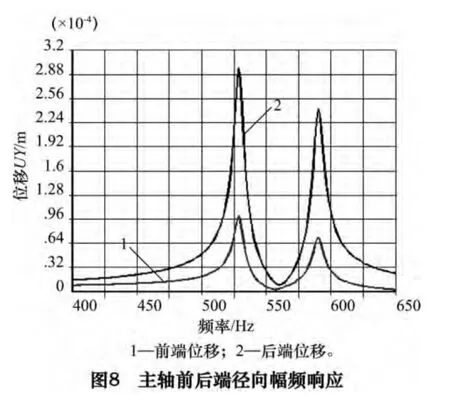
轴承支撑位置的位移-频率响应曲线如图9 所示,其峰值频率点与图8 一致,且后端轴承支撑点5 的位移响应峰值明显大于前端轴承支撑点1、2、3、4,说明主轴前端轴承支撑点具有较大动刚度,能够有效拟制切削过程中的主轴径向变形及振动。由谐响应分析可知,在两个共振频率点529 Hz 与590 Hz 处,陶瓷电主轴会产生较大位移响应,为了保证主轴系统稳定运行和避免共振发生,机床工作转速应尽量避开共振频率及其附近区域。
从国家层面:由于中美两国经济合作时间已近30年,双方合作的领域数目较多,所以中美贸易摩擦在不断加剧的同时,导致涉及的经济领域范围也在不断扩大。同时也对政策和制度等宏观领域造成了不利影响,导致了我国对外贸易的弱势。此次贸易摩擦严重影响了两国之间的经济氛围,双方人民不便在市场中获取价格相对低廉的进口产品,影响民众生活质量。站在整个世界经济的角度来看,美国单方面挑起贸易摩擦不利于世界经济的复苏和发展。
5 动力学优化
以陶瓷电主轴支撑跨距d1、d2为设计变量,采用随机搜索算法对其进行动力学优化设计。该电主轴设计工作转速在30 000~40 000 r/min,由前文计算可知主轴的一阶临界转速C1=31 740 r/min,为了进一步增大主轴稳定工作转速带宽范围,要求尽量提高其一阶临界转速,也就是提高主轴系统一阶共振频率,使其适应更高的工作转速,故以提高一阶临界转速C1为优化目标,建立如式(7)所示的优化目标函数,其中C1是以d1、d2为自变量的函数,C1i为第i 次优化计算得出的临界转速值,f1为陶瓷电主轴一阶共振频率。
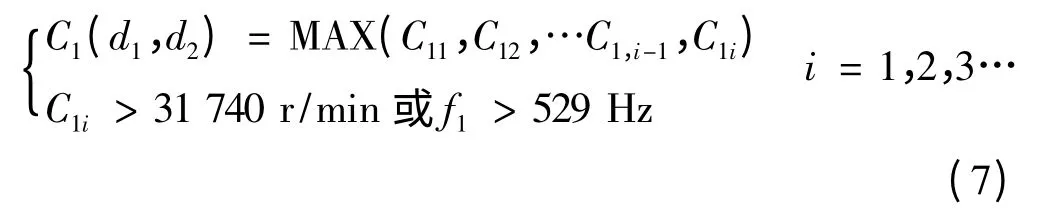
设计变量的随机采样曲线如图10 所示,通过对不同的d1、d2采样值进行组合计算,可以获得相应的临界转速值,根据式(7)可知,计算结果中的最大值即为一阶临界转速最优值。由图11 可知,系统共进行了7 次采样计算,其中第6 次计算结果数值最大,即C16=32 675 r/min 为一阶临界转速的优化值,相对于优化前提高了2.95%,符合优化设计目标。另外,优化结果还使主轴支撑跨距d1、d2发生了变化,如表4 所示,d1、d2分别增大至65.81 mm 和224.28 mm,说明主轴在这一支撑位置具有更好的动力学特性。与此同时,主轴系统的一阶共振频率也由之前的529 Hz 提高至544.58 Hz,有效增强了陶瓷电主轴的抗振性能,有利于主轴系统的高速化发展。

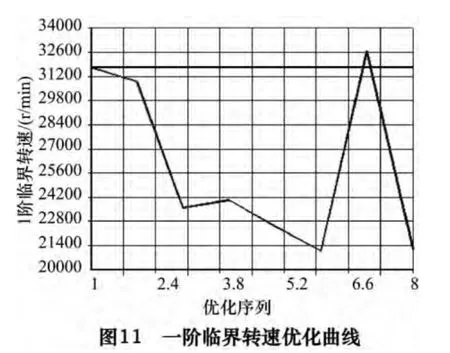
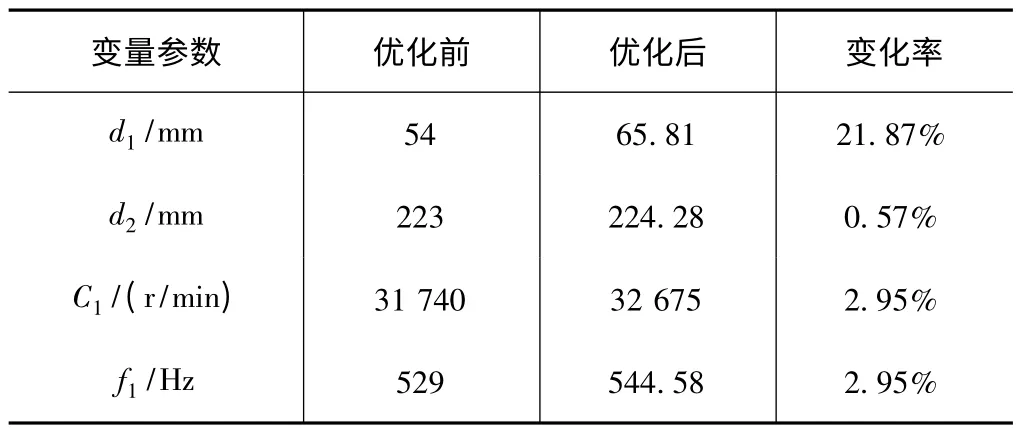
表4 一阶临界转速优化结果数据
6 结语
本文将陶瓷材料Si3N4应用于高速电主轴,以动力学理论为基础,结合参数化建模、有限单元法、动态分析及优化技术等现代设计方法,对其动力学特性展开深入研究,主要得出以下几方面结论:
(1)相对于钢制电主轴,陶瓷材料Si3N4可以显著提高电主轴各阶自振频率,使其抗振性能得到有效增强,可见陶瓷材料对于改进电主轴动力学特性具有重要的应用价值。
(2)在0~40 000 r/min 转速范围内对陶瓷电主轴进行模态分析,由campbell 图确定了该主轴系的一阶临界转速C1=31 740 r/min、二阶临界转速C2=31 740 r/min,为数控机床的工作转速调节与控制提供了重要依据。
(3)通过谐振响应分析获得了陶瓷电主轴的位移-频率响应,计算出了主轴的位移响应峰值,明确了共振频率点及其对主轴薄弱部位的影响。
(4)在参数化建模基础上实现了陶瓷电主轴的一阶临界转速优化,使其比优化前提高了2.95%,增大了主轴系统的安全工作转速范围,为陶瓷电主轴的高速化设计提供了支持。
[1]陈小安,刘俊峰,合烨,等.高速电主轴热态性能及其影响[J].机械工程学报,2013,49(11):135 -142.
[2]刘小文.全陶瓷电主轴主轴精密加工实验研究及动态性能分析[D].沈阳:沈阳建筑大学,2011.
[3]邱海飞.数控机床主轴部件静动态特性优化设计[J].现代制造工程,2013(11):68 -70.
[4]邱海飞,吴松林.DG46 多级泵转子组件动力学建模与分析[J].矿山机械,2013,41(2):60 -163.
[5]张国通.高速陶瓷电主轴设计及动静态性能分析[D].秦皇岛:燕山大学,2011.
