寄生时栅式电动机的感应信号非接触式提取方法*

刘世友 彭东林 付 敏 吴治峄 王淑娴 李 云

(①重庆理工大学机械检测技术与装备教育部工程研究中心，时栅传感器及先进检测技术重庆市重点实验室，重庆 400054;②重庆大学机械传动国家重点实验室，重庆 400044;③湖南五凌电力有限公司，湖南 长沙 410004)

准确、可靠的转子位置及速度检测是实现伺服电动机高性能控制的必要条件［1］。通常检测转子信息的方法有两类:无传感器技术和传统的机械传感器技术。无传感器技术利用电动机本身运行的特性，通过建立数学模型对电动机位置进行估测。但各类型的无传感器技术都依赖于假定电动机本身的参数始终不变，而实际上这些量在电动机运行过程中是变化的，其准确性和精度都不可能达到很高，同时该方法仅适用于某些结构上具备“凸极性”的电动机，且不能在全速度范围实现位置检测，其应用范围很窄［2-3］。

传统的方法多采用光电编码器。该方法精确度很高［4］，但其显著缺点是机械安装工艺困难、一般需改变电动机主轴的尺寸和结构;可靠性较差、易受电动机轴频繁抖动干扰的影响，降低了系统的控制性能;此外，高精度光电编码器价格昂贵、成本高、不易维护［5］。

因此，寻找一种既不破坏电动机自身结构，又能在电动机内部嵌入一种专门的位置传感器，实现全速度范围精密位移检测的方法，是解决电动机位置检测的最佳方向。因时栅结构与电动机有着“孪生”的关系，所以将时栅位移传感器植入到异步电动机的原有结构中，得到一种全新的“寄生时栅式电动机”，从而获取电动机转子位置及速度信息［6-8］。这样有利于解决目前各种用于电动机位置和速度检测方法中存在的精度低、抗干扰能力差、适用性不强、成本高等问题。

文献［6 -7］中实现了将时栅激励信号和电动机驱动信号调制后稳定有效地注入异步电动机当中。如何将转子产生的感应信号提取至时栅控制器成为我们的亟需解决的问题。转子无法通过接线方式来实现信号提取，而电刷引线是解决此类问题的常用方法。由于电刷的磨损，以及产生电火花的影响，其可靠性不高［8-9］。此方法可基本实现信号的输出，但其本身的缺陷使得输出的效果差、实现难度高。

本文以寄生时栅式电动机为研究对象，建立了数学模型，找出了影响信号提取的各种因素，并对两个关键因素进行了仿真。结合分析设计出了非接触式电磁耦合变压器，并通过实验验证。

1 寄生时栅式电动机信号非接触提取工作原理

非接触式信号传输系统原理如图1 所示。调制后的时栅信号和电动机驱动信号加载于异步电动机三相绕组中，电动机内部产生旋转磁场，旋转磁场扫描位于转子处的动测头线圈产生感应信号。经过滤波后，得到反映时栅位置和速度的信号，然后输入到非接触式高频耦合变压器的原边线圈。再将副边线圈电磁耦合信号提取至时栅控制器，经处理后得到电动机转子的位置和速度信息。

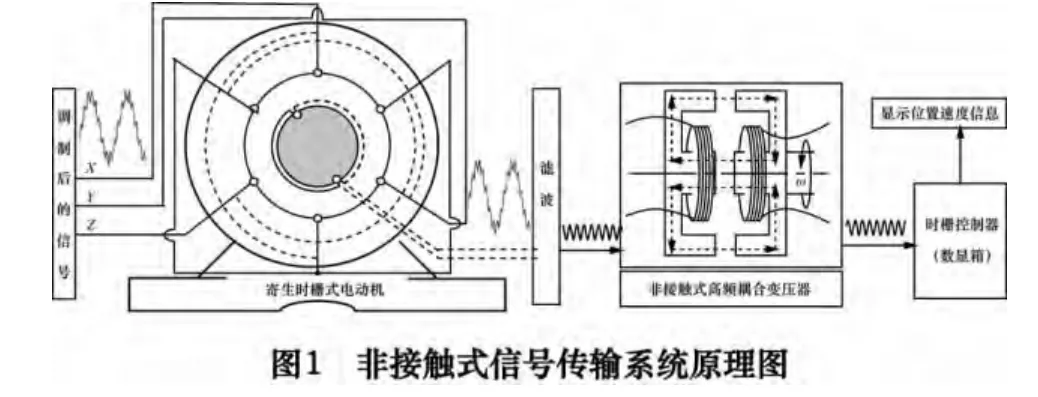
在上述过程中，非接触式高频耦合变压器是实现信号提取的关键，其原理如图2 所示。

在转轴上布置两个并排的线圈，使其轴线一致，一个固定在转轴上随转轴旋转，另一个固连在基座上。若在其中一个线圈中通以交变电流，其产生的交变磁场将通过另一线圈，从而产生交变感应电势，如此便实现了信号非接触式提取。由于线圈为圆形，一个线圈相对另一线圈同轴转动时，穿过副边磁力线不会发生变化，从而其互感不会变化，这样保证了旋转时信号提取不受转速的影响。

2 非接触式高频耦合变压器模型分析

由于非接触式高频耦合变压器原、副边线圈之间有较大气隙存在，使漏磁较大，耦合系数较小，电信号传输能力和效率较低，因此不能按照常规变压器模型对系统进行分析，必须建立合适的模型。本文利用互感模型来分析非接触式高频耦合变压器原、副边线圈之间的耦合能力，这种模型能简单且准确地反映信号的传输关系。

图3 中，ω 为输入信号频率;M 为互感系数;I1、I2分别为原、副边电流;C1、C2分别为原、副边补偿电容;L1、L2分别为原、副边自感系数。

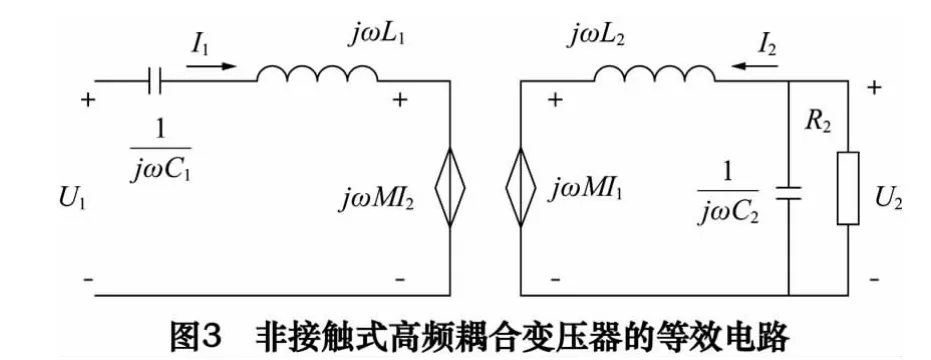
由图3 得输出电压U2为

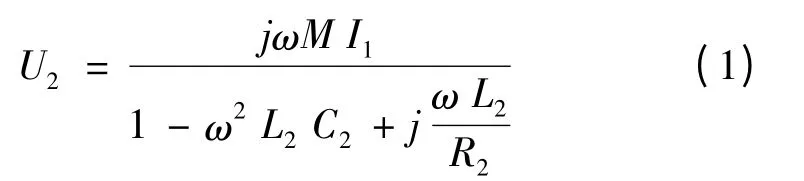
由式(1)可知，增大输出电压U2，需增大副边线圈感应电压jωMI1。通过选择副边侧补偿电容C2，使ω2L2C2=1，减小式(1)分母项模值，从而增大U2，则由式(1)得:

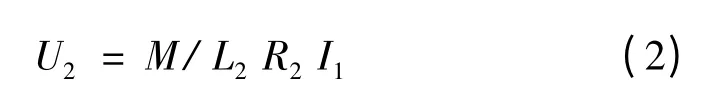
输出功率:

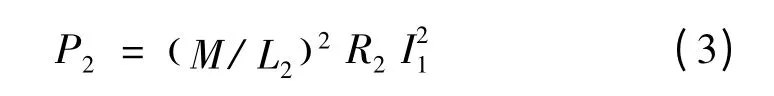
为便于分析，假定非接触式高频耦合变压器原、副边线圈所用的磁芯相同，线圈的匝数及绕制方法相同。用图4 所示等效磁路进行分析。

图4 中，Φm是主磁通;φs是漏磁通;Φ 是初级线圈产生的总磁通;Rs是耦合变压器的漏磁阻;Rg是气隙磁阻;Rc是磁芯本身的磁阻;E 为电路本身的磁动势。通过磁路分析可得耦合系数K 为:

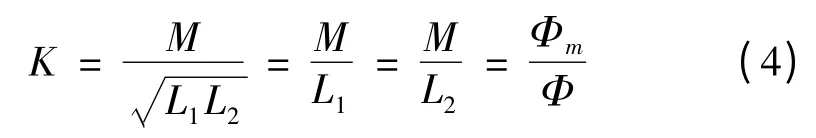
由磁路的KVL 可得:

磁芯确定后其本身的磁阻也随之确定，因此影响互感与原副边自感比值的本质因素为Rs与Rg。减小Rg或增大Rs都能增大耦合系数K。根据磁阻定义，Rg与气隙长度成正比，与气隙磁路面积成反比。由式(5)可以看出，影响耦合系数K 的主要因素包括磁芯的材料(决定其本身磁阻RC)、相对位置以及气隙大小(决定其漏磁阻Rs与气隙磁阻Rg)。结合式(1)、(2)、(3)、(5)得出，提高U2、K、P2途径主要有:减小气隙长度;增大原边线圈输入电流频率、幅值;选择具有较小铁芯损耗、较高的电阻率和饱和磁感应强度的高频导磁铁芯;增大磁路面积。

3 非接触式高频耦合变压器结构设计

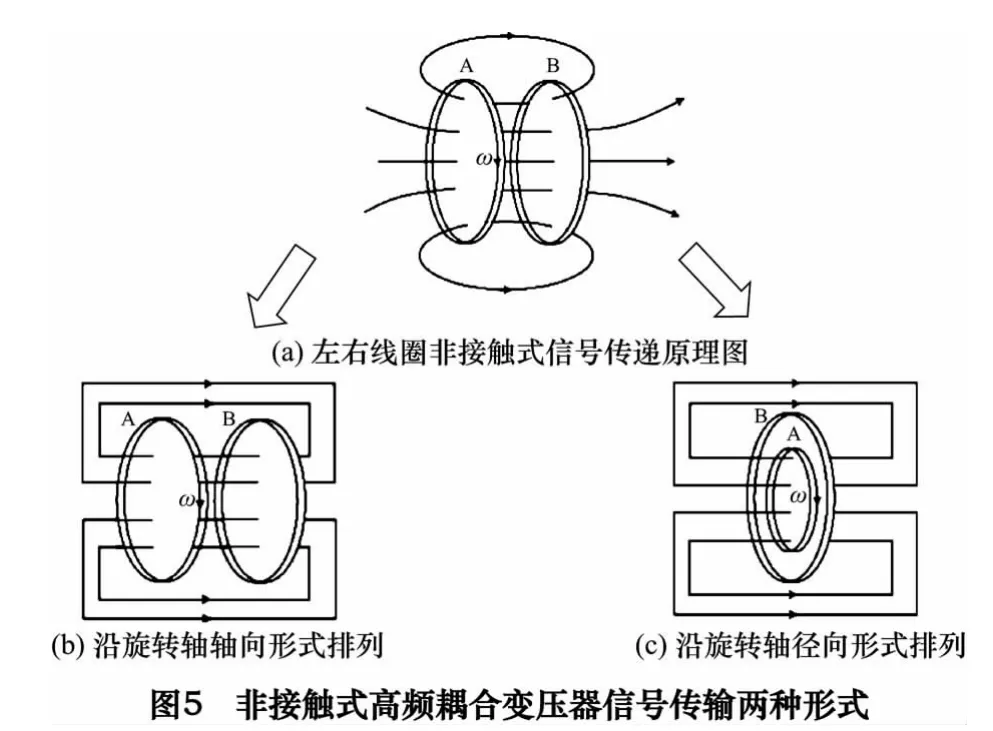
由非接触式高频耦合变压器原理(图5a)可知，只要保持左、右边线圈A、B 的相对位置，就可实现旋转部分与静止部分之间信号的非接触信号提取。根据时栅定、转子之间的信号传递形式可将其原、副边线圈的排列分为沿旋转轴轴向排列和沿旋转轴径向排列，其结构如图5b、5c 所示。

由于原、副边线圈径向排列产生的Rs较大，加工、安装方面也存在一定的困难，因此选择轴向排列。

线圈轴向排列确定后，磁路的走向也就定了下来。依据试验用电动机转子主轴与端盖的尺寸和之前的理论分析，选用了具有较小铁芯损耗、较高电阻率和饱和磁感应强度的高频导磁锰锌铁氧体罐形铁芯(GU72)。

为防止原、副边线圈发生抖动，用非磁性且非导电的塑钢材料制作成线圈支架，可保持线圈形状并且避免线圈与铁芯接触导电。变压器的表面包裹有铜膜可以屏蔽外部电磁干扰。实物结构如图6 所示。

4 仿真分析

由非接触式高频耦合变压器的原理可知:影响其信号传输效果最主要的是输入电流的频率和气隙的大小。因此对这两个参数进行仿真分析。为了分析方便，在仿真时将磁芯设为线性导磁材料，相对磁导率为2 300，电导率为100 s/m，负载固定为20 Ω，不考虑涡流损耗。

4.1 输入电流频率与输出感应信号的关系

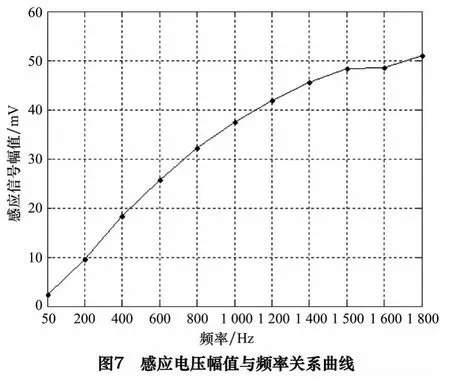
在变压器气隙为0.5 mm，原边电流为0.1 A 时，从图7 中可以看出，随着频率的增加，输出电压的幅值逐渐增加，当频率增至1 500 Hz 继续增加时，幅值增加并不明显。由此可知，1 500 Hz 的频率可大大提高输出电压的幅值。

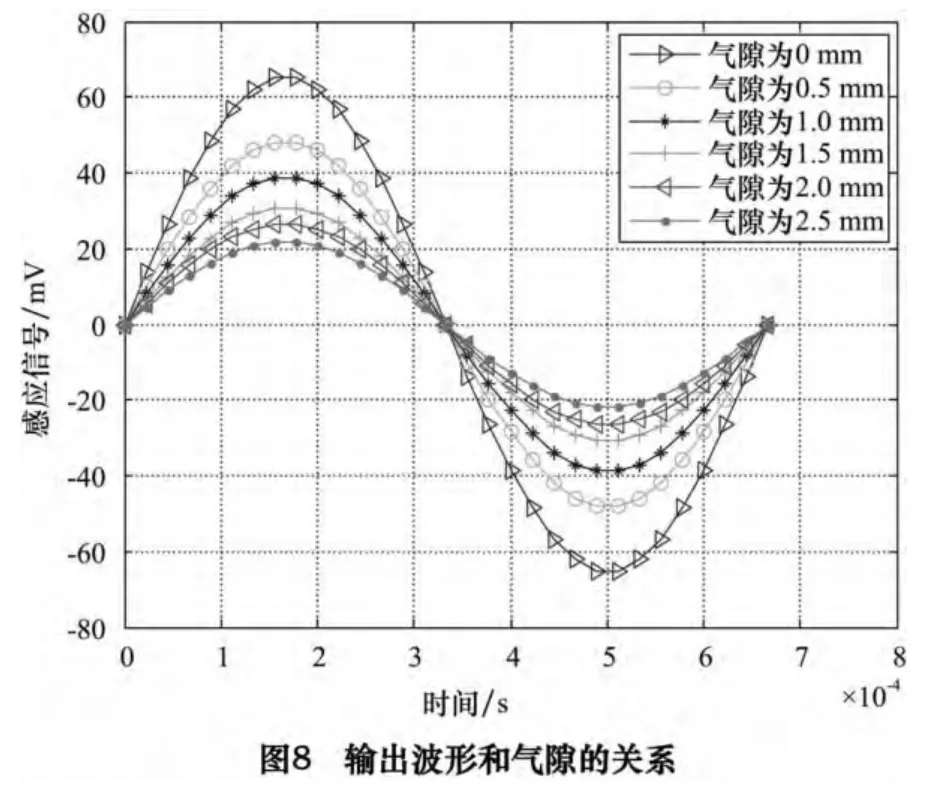
4.2 气隙与输出感应信号的关系

当频率固定为1 500 Hz，对不同气隙进行仿真，得出输出波形和气隙的关系如图8 所示。从图8 中可以看出，气隙在1.5 mm 以内时，随着气隙的增加，输出电压幅值下降快，当气隙增至1.5 mm后，幅值的变化很小。因此在满足实际的生产工艺和定位安装的要求下，减小气隙，可有效提高输出信号的质量。

5 实验

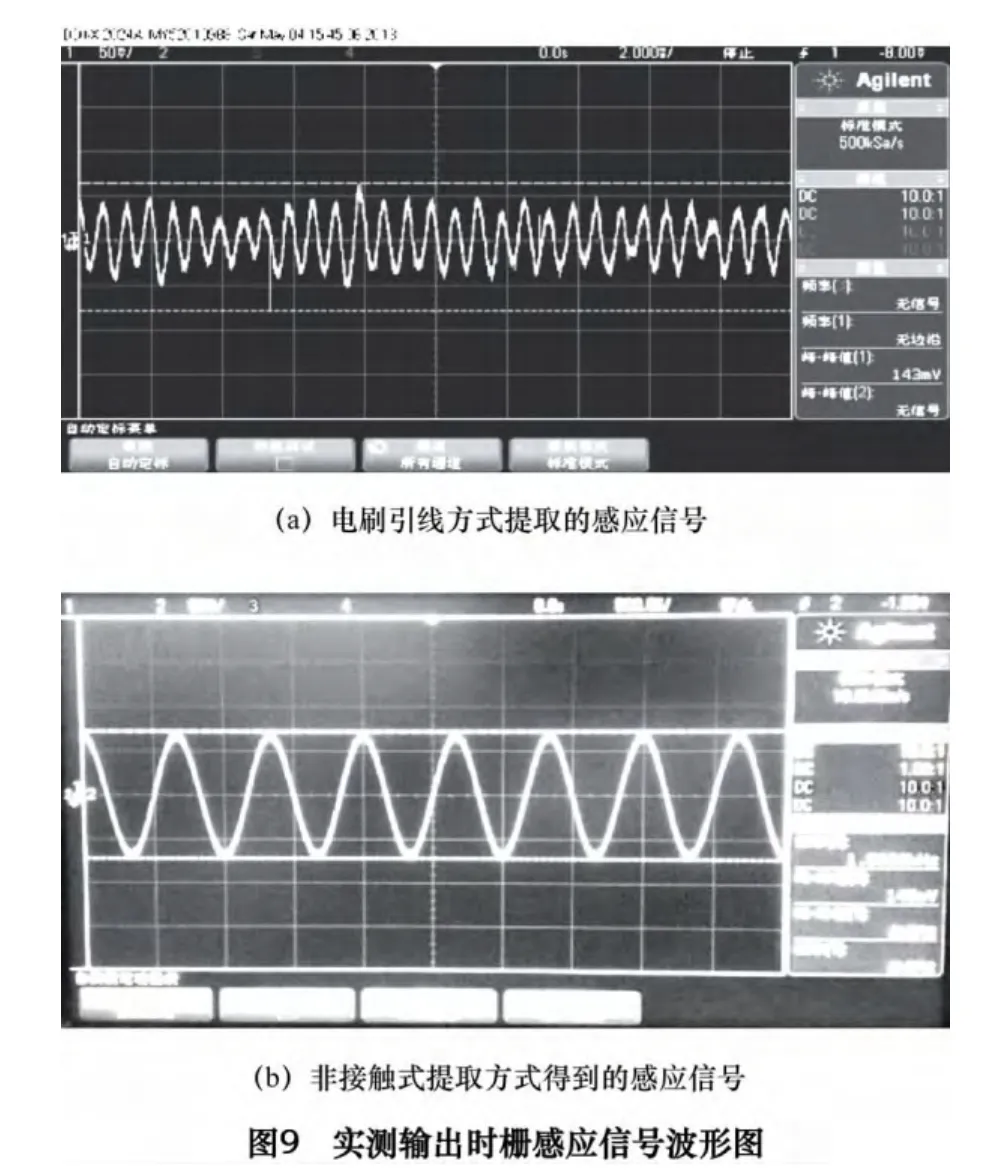
依据仿真分析与实际的生产工艺和定位安装的要求，将时栅激励信号和电动机驱动信号频率分别设为1 500 Hz、50 Hz，非接触式电磁耦合变压器的气隙为0.5 mm，实验结果见图9。

由图9 可以看出，电刷引线方式提取的信号波动明显，非接触式提取方式提取信号的质量明显优于电刷引线方式的。

6 结语

通过所建模型的理论分析，找出了影响寄生时栅式电动机的非接触式高频耦合变压器U2、K、P2的因素，通过仿真，确定了影响提取信号质量的两个关键参数为变压器的气隙和输入信号频率的最优值。

结合上述因素与实验电动机具体情况设计出了非接触式高频耦合变压器。最后通过实验验证了非接触式高频耦合变压器能很好地实现时栅感应信号非接触提取。相比较常规的电刷引线的方法，避免了摩擦接触引起的信号波动、磨损和发热，并且可以依据电动机的尺寸，设计相应的非接触式高频耦合变压器，降低了信号提取的实现难度。

［1］吴忠，吕绪明.基于磁编码器的伺服电机速度及位置观测器设计［J］.中国电机工程学报，2011，31(9):82 -87.

［2］秦峰，贺益康，刘毅.两种高频信号注入法的无传感器运行研究［J］.中国电机工程学报，2005，25(5):116 -121.

［3］刘毅，贺益康，秦峰.基于转子凸极跟踪的无位置传感器永磁同步电机矢量控制研究［J］.中国电机工程学报，2005，25(17):121 -126.

［4］于庆广，刘葵，王冲，等.光电编码器选型及同步电机转速和转子位置测量［J］.电气传动，2006，36(4):17 -19.

［5］王峰，张波，丘东元.交流电机的虚拟光电编码盘测速技术［J］.中国电机工程学报，2005，25(6):99 -103.

［6］彭东林，陶飞亚，付敏，等.时栅激励信号载波注入异步电机方案的设计与实现［J］.自动化仪表，2014，35(6):1 -3.

［7］陶飞亚，彭东林，付敏，等.寄生时栅式电机的载波信号三相不平衡分析与优化设计［J］.电机与控制应用，2014，35(6):88 -90.

［8］Boys J T，Green A W.Inductive power distribution system:US，5293308［P］.March 8，1994.

［9］Eghtesadi M.Inductive power transfer to an electric vehicle-analytical model［A］//IEEE Conference on Vehicular Technology ［C］.1990，40:100 -104.