基于分子生物技术的DNA计算系统*
2014-04-22李燕,钟磊
李 燕,钟 磊
(南京信息工程大学 计算机与软件学院,江苏 南京 210044)
0 引言
NP完全问题是不确定性图灵机在多项式时间内能解决的问题,是国内外算法研究领域的热点和难点。P=?NP问题的研究受到科学家们的高度重视,开辟模拟生物智能的新路已成为人们研究NP问题的新方向。在智能化领域的探索过程中,人们意识到研究智能的最好方式是模仿生物特性向人类自身学习。美国加州工学院物理学家Hopfield采用Hopfiled神经网络模型,对旅行商最优路径问题进行了研究。美国 Michigan大学的 Holland[1]教授,以达尔文的生物进化论和孟德尔的遗传变异理论为基础,提出了遗传算法,在思路上突破了原有最优化方法的框架。这对NP问题的研究起到了极大的促进作用,很多学者纷纷采用这种模拟生物系统的方法解决NP问题,但对于NP完全问题仍然没有有效的通用解决办法。1994年,美国加利福尼亚大学的Adleman[2]教授第一次利用现代分子生物技术,提出了有向哈密尔顿路径问题的DNA(deox-yribonucleic)分子计算方法,并成功地在DNA溶液的试管中进行了实验,这一实验在国际上引起了巨大的反响。科学家认为将DNA分子碱基排列的性质用于尝试数学计算,是跨生命科学与计算科学两大学科的一个崭新的研究领域。从遗传进化、人工神经网络和DNA分子生物技术对智能的模拟过程来看,它们分别对应生物群体、生物神经元和生物分子3个截然不同的层次。由此可以看到,DNA计算的研究不仅是解决复杂类问题的突破口,而且有可能更深刻地揭示智能形成的本质[3-8]。
本文主要介绍DNA分子的结构及计算模型,针对目前初始化过程存在的不足,提出数据初始化模型,给出了DNA分子初始化模型的算法描述;阐述DNA计算系统的设计与实现,该系统成功地模拟生物DNA计算过程,避免了生物实验中的误差。
1 DNA计算模型
1.1 DNA分子的结构
DNA是一种高分子化合物,称为脱氧核糖核酸,是遗传信息存储的媒介,它的分子结构图如图1所示。
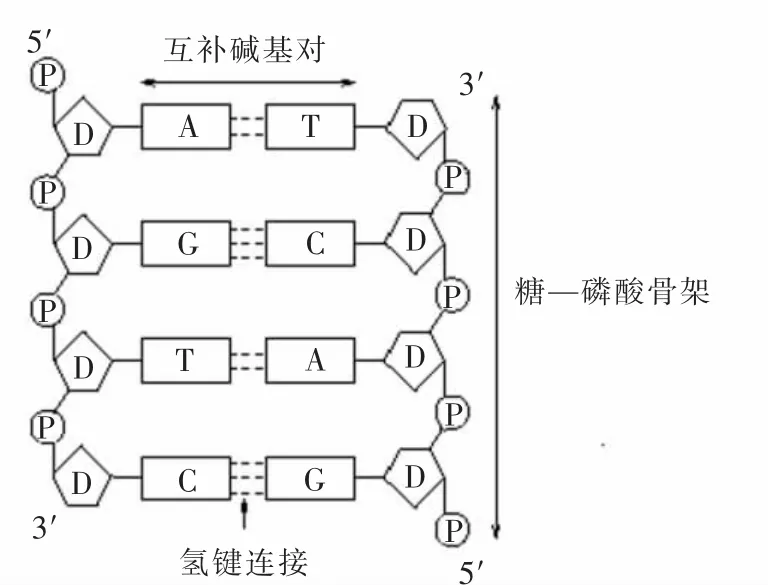
图1 DNA分子结构图Fig.1 Structure of DNA molecules
组成DNA的基本单位是脱氧核苷酸,组成脱氧核苷酸的含氮碱基有4种,它们是腺嘌呤(A)、鸟嘌呤(G)、胞嘧啶(C)和胸腺嘧啶(T)[5]。多个脱氧核苷酸一个连一个,形成脱氧核苷酸链。DNA大分子是由2条头尾方向相反的脱氧核苷酸长链,以右手螺旋的方式盘绕着同一中心轴而形成的。2条链上的碱基通过氢键连接起来,碱基对的连接严格依据碱基互补配对原则,即腺嘌呤(A)通过2个氢键与胸腺嘧啶(T)配对,鸟嘌呤(G)通过3个氢键与胞嘧啶(C)配对。反过来也必定是T与A配对、C与G配对。遗传信息是以A,T,C,G在核苷酸中的排列顺序而体现的,其排列的多样性构成了丰富的遗传信息。
1.2 DNA剪接操作
DNA分子重组包括2个步骤:第1步,2个DNA双链分子在限制性核酸内切酶识别的位置上被分别切割;第2步,在连接酶的作用下重组粘接,形成新的DNA分子。剪接操作是DNA分子重组的数学抽象[9],它只表示分子上链的变换,通过互补关系可推出下链的分子序列。上链的默认方向是5′→3′。形式化描述剪接操作需引入符号:字母表Σ以及Σ上的2个字符串x和y分别表示DNA分子a和DNA分子b,剪接规则r是Σ上形式为α1#β1$α2#β2的字符串,其中,α1,β1,α2,β2∈Σ*,$,# ∉Σ,$ 和#仅作为标记符号。2个表示DNA分子的字符串x=x1α1β1x2与y=y1α2β2y2,按照 剪 接 规 则r=α1#β1$α2#β2,单输出的剪接操作表示为(x1α1|β1x2,y1α2|β2y2)⇒x1α1β2y2。
定义1 剪接计算模型为四联体Ψ= (Σ,T,A,R),其中:
(1)Σ是字母表;
(2)T⊆Σ是终结符号;
(3)A⊆Σ*是开始符号的集合;
(4)R⊆Σ*#Σ*$Σ*#Σ*是规则集合。
定理1 任意一个递归可枚举型语言,都可由相应的剪接计算模型来产生。
证明 设G= (N,T,S,P)为0型文法。构造剪接模型Ψ= (Σ,T,A,R),其中:Σ=N∪T∪{B,B′,S0,E,C,C1,C2}∪ {Eα|α∈N∪T∪{S0}}。符号B,B′作为剪接字符串的最左端标记;符号E,Eα作为剪接字符串的最右端的标记;符号S0用于标记文法G中被模拟推导的字符串开始位置。

规则集R包含以下限制规则:
模拟规则:模拟文法G中产生式u→v∈P。
(1)r= (#uE$C#vE;{B},φ)。
移动规则:将字符串中的u移到右端。
(2)r= (#αE$C#Eα;{B},φ)。
(3)r= (B#$B′α#C;{Eα},φ)。
(4)r= (#Eα$C#E;{B′},φ)。
(5)r= (B′#$B#C;{E},φ)。
终止规则:结束剪接操作。
(6)r= (BS0#$#C′;{E},φ)。
(7)r= (#E$C″#;φ,φ)。
剪接模型的模拟推导从字符串BS0SE开始。如果当前字符串的形式为Bx1S0x2uE,可使用模拟规则(1)来模拟文法G中的产生式规则u→v∈P。否则,通过转换规则(2),(3),(4),(5)将u移动到字符串的右端。转换过程如下。
设u右边的字符串为α,α∈N∪T∪{S0},符号BwαE表示整个字符串,w∈ (N∪T∪ {S0})*。
按照 规 则 (2),(Bw|αE,C|Eα)⇒(BwEα,CαE),Eα保存了被切割掉的内容。这个操作生成了2个新的字符串,由于BwEα包含Eα,符合规则(3)的限制条件,所以字符串BwEα参与下一步的剪接操作。
按 照 规 则 (3), (B|wEα,B′α|C)⇒(BC,B′αwEα),这里的α与规则(2)的α内容相同。新字符串中的B′αwEα符合规则(4)的限制条件。
按照规则(4),(B′αw|Eα,C|E)⇒(B′αwE,CEα)。新字符串中B′αwE符合规则(5)限制条件。
按 照 规 则 (5),(B′|αwE,B|C)⇒(B′C,BαwE),通过转换规则,字符串BwαE转换成了BαwE,此时u移动到了αw的右端,可以使用规则(1)进行剪接操作。
按照规则(1),(Bw|uE,C|vE)⇒(BwvE,CuE)。
模拟规则和转换规则可以根据需要,迭代使用。
按照结束规则进行剪接操作,可得到终结符串。
按照 规 则 (6),(BS0|wE,|C′)⇒(BS0C′,wE),w⊆T*。
按规则(7),(w|E,C″|)⇒(w,C″E),w⊆T*。
通过上述的推导过程可知,凡是文法G能产生的语言,剪接模型都能产生。所有图灵机可计算的问题理论上都可以通过DNA计算来完成。
1.3 DNA计算过程
完整的DNA计算过程包括数据输入、运算以及结果的输出[10-11]。具体步骤如下:
步骤1 通过对问题的分析,设计合理的编码模式,将问题空间的对象映射成DNA分子链,在试管中构建出所有可能解的初始数据,形成初始数据集合。
步骤2 利用DNA分子链的高度并行运算的特点,用可控的分子生物操作完成正确答案的筛选,不同的计算模型,选择的操作过程及技术不同。
步骤3 结果的输出。这一步通过测定来判断是否有解,如果有解则将DNA链进行译码,就是所求问题的解。
以上计算涉及到的分子生物技术有:聚合酶链式反应、凝胶电泳、亲和层析、加热/退火、克隆、磁珠分离、标记、合并、连接、切割、检测等。
1.4 数据初始化模型
DNA计算处于起步阶段,充满机遇和挑战。一些研究人员曾经重复了Adleman的试验,他们按照Adleman的设计方法及步骤严格进行了试验,但没得到计算结果。这说明除了实物试验方面存在的误差外,还有可能是初始化数据不理想,在初始数据随机组合时,没有产生表示实际解的DNA链,那么无论怎样筛选都不会找到问题的解。为解决这一问题,本文提出了数据初始化模型,该模型通过编码控制方式控制数据的初始化。
将表示问题解的DNA链的编码模式设计为v1ek1v2ek2…vnekn的形式。其中,vi表示第i个位置的编码,i∈1,2,…,n。eki表示第i个位置所携带的信息编码。令表示问题的所有信息短链的编码集合为E,第i个位置所携带的信息编码的集合为Ei,Ei⊆E。用符号card(Ei)表示集合Ei中所包含的元素个数。集合Ei中的元素按照1,2,…,card(Ei)的顺序依次排列,每一个位置i只能携带集合Ei中的一个元素eki,k∈1,2,…,card(Ei)。模型中需要用到的分子操作方法有:
(1)集 合 复 制,Copy({T1,T2,…,Tn},T)。并行地将试管T中的DNA分子全部复制,产生n个与T中的内容相同的试管Ti,即产生与集合T内容相同的n个集合Ti。
(2)DNA链右边追加短链,Rappend(T,x)。并行地将试管中所有DNA链的右端连接DNA短链x,Tx:={wx|w∈T}。即将集合T中的所有元素添加一个后缀x。追加前试管T可以为空。
(3)合并,Union(T,{T1,T2,…,Tn})。并行地将n个试管中的DNA溶液合并到试管T中,T:=T1∪T2…∪Tn,即n个集合Ti合并产生了集合T。
(4)析取,Extract(T,x)。并行地析取出试管T中包含有子串x的DNA分子链。
数据初始化模型Initialization(T)的算法描述如下:
begin
fori=1 tondo
begin
Copy({T1,T2,…,Tcard(Ei)},T);
fork=1,2,…,card(Ei)in parallel do
Rappend(Tk,vieki);
Union(T,{T1,T2,…,Tcard(Ei)});
end
end
应用上述数据初始化模型控制数据的初始化过程,保证了初始数据的完整性,不会造成解的丢失,也不会产生与实际解的模式不相同的DNA链。该模型不仅为后续的计算过程奠定了良好的基础,而且减少了计算过程中参与筛选的DNA链的数量,从而减小了计算误差。
2 DNA计算系统
2.1 系统概述
因受现有生物技术限制,活性DNA反应时间较长,材料成本高,在实验室较难完成实际分子计算过程。针对这一现状,开发了仿生DNA计算系统,系统开发工具为Vc++6.0。DNA计算系统应用DNA分子的结构特性和常用分子生物操作过程,以DNA编码串作为信息的载体,以生物操作为算子,采用上述数据初始化模型产生初始数据,模拟DNA分子计算过程。DNA计算系统包括5大模块:
(1)DNA基础知识。介绍DNA分子双螺旋结构、特性。
(2)常用DNA分子操作技术。
(3)DNA计算模型。包括DNA分子的演算过程、DNA自动机、DNA分布式计算以及算法描述。
(4)DNA计算系统仿真。该模块模拟DNA生物操作过程解决计算问题,包括问题的输入、计算过程模拟、结果输出。
(5)开放性问题探讨。应用网络资源广泛进行交流和探讨。
2.2 应用实例
本文以查找6个城市间的哈密尔顿路径问题为例,介绍DNA计算过程。数字0,1,2,3,4,5分别代表6个城市,假设城市1为起点,城市4为终点,如图2所示。
DNA计算系统仿真过程如下。
步骤1 问题输入。分别输入节点数、节点名称、边、起点和终点。节点编码分别由4种碱基A,T,C,G组成的DNA链表示,用户可以手工输入各个节点编码,也可以点击按钮,由系统自动生成编码。本例的节点编码由8位DNA碱基序列构成。点击“城市名称”按钮,可自动生成分别表示6个城市名称的DNA编码。系统模拟生物操作过程执行数据初始化算法组合路经,生成初始数据集合。
步骤2 DNA计算过程。点击“找哈密尔顿路”按钮,模拟生物操作过程,依次比较节点和边的连通序列,按约束规则求解问题,该过程是DNA计算系统仿真模块中最主要环节。仿真模拟界面如图3所示。
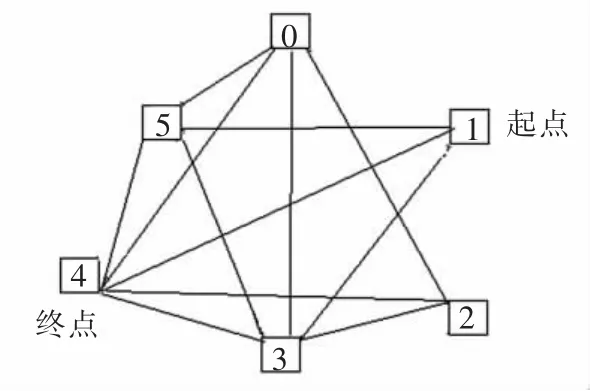
图2 6个城市的哈密尔顿路径问题图Fig.2 Hamilton path problem in 6cities
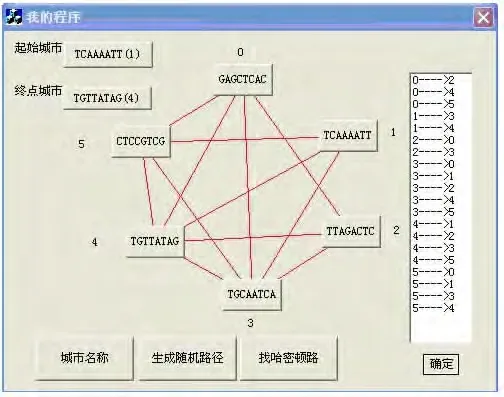
图3 仿真模拟界面Fig.3 Simulation interface
步骤3 输出结果。执行步骤2后,如果找到路径,弹出的对话框给出从起始城市到终点城市的哈密尔顿路径;若没找到路径,对话框提示该问题无解。本例找到的路径编码序列为TCAAAATT—TGCAATCA—TTAGACTA—GAGCTCAC—CTCCGTCG—TGTTATAG,解码译成相应的城市名称,1—3—2—0—5—4就是所求结果(见图4)。
3 小结
作为新生事物的DNA计算方法,引起了科学家们的广泛重视,人们对DNA计算的前景充满希望。DNA计算拓宽了人们对自然计算现象的理解,特别是对计算本质的理解。通过模拟生物DNA分子操作技术抽象出的DNA计算模型,使人们认识到DNA计算也是一种递归计算。就计算本质而言,它同人类有史以来的一切计算都是等价的、一致的。所有图灵机可计算的问题理论上都可以通过DNA计算来完成。但由于是起步阶段,DNA计算还存在着许多亟待解决的问题。仿生DNA计算系统成功地模拟生物DNA计算过程,避免了生物实验误差,节约材料成本,减少活性分子在试管溶液中的反应时间,为DNA计算从原理性的实验向实际应用奠定基础。相信随着科研人员的不懈努力和探索,DNA计算一定会真正应用于工程实践中。

图4 DNA计算结果图Fig.4 DNA computing result
[1] HOLLAND J H.Adaptation in Natural and Artificial System:An Introduction Analysis with Application to Biology,Control and Artificial Intelligence[M].Michigan:the University of Michigan Press,1975.
[2] ADLEMAN L M.Molecular computation of solutions to combinatorial problems[J].Science,1994,266:1021-1024.
[3] LIU Q H.DNA computing on surfaces[J].Nature,2000,403:175-179.
[4] LIM H W,LEE S H,YANG K A,et al.In vitro molecular pattern classification via DNA-based weightedsum operation[J].Biosystems,2010,100:1-7.
[5] DAREHMIRAKI M.A new solution for maximal clique problem based sticker model[J].Biosystems,2009,95:145-149.
[6] SMITH D H,ABOLUION N,MONTEMANNI R,et al.Linear and nonlinear constructions of DNA codes with Hamming distanced and constant GC-content[J].Discrete Mathematics,2011,311:1207-1219.
[7] 周康,同小军,刘文斌,等.最短路问题的闭环DNA算法[J].系统工程与电子技术,2008,30(3):556-560.
[8] MARDINAN R,SEKIYAMA K,FUKUDA T.Approaching mathematical model of the immune network based DNA strand displacement system[J].Biosystems,2013,114(3):245-252.
[9] KARI L.DNA computing:arrival of biological mathematics[J].The Mathematical Intelligence,1997,19(2):9-22.
[10] 周旭,李肯立,乐光学,等.一种最大匹配问题DNA计算算法[J].计算机研究与发展,2011,48(11):2147-2154.
[11] 薛洁,刘希玉.基于DNA计算的层次图聚类算法[J].计算机工程,2012,38(12):188-190.
