分数阶偏微分方程的完全小波配置解法
2014-04-22李新秀
李新秀
(南京邮电大学 理学院,江苏 南京 210046)
0 引言
近几十年,分数阶微积分已经从纯数学理论研究逐渐转到实际应用的研究。与整数阶导数相比,分数阶微分算子是非局域算子,具有历史记忆性,更适合描述具有记忆和遗传效应的物理现象,所以近年来分数阶微分算子不断的被应用到物理和工程中来。关于分数阶导数的详细描述参考[1]。本文中的分数阶导数都是指Caputo意义下的导数:

其中 m≤α<m+1.
分数阶微分方程要方便应用于实践,关键在于分数阶微积分数值计算。 然而,分数阶微积分方程的数值方法及其理论分析是十分困难的课题。分数阶微积分数值计算中涉及的主要问题:其一是需存储整个历史数据,随着时间的增加,信息量不断增加,计算工作量急剧增加;其二是当时间不断增加时,离散误差很难进行控制,从而可能导致计算数据的失真。鉴于此,研究可行有效的分数阶微分方程数值计算方法是十分有意义的。
文献[3]把三次样条小波配置方法成功推广到一元分数阶微分方程的数值求解中。本文的目的是利用完成小波配置方法求解分数阶微分方程的数值求解。
1 分数阶偏微分方程的三次B-样条小波配置方法
本节我们考虑用完全小波配置方法求解分数阶偏微分方程的初边值问题。蔡和王在文献[4]中给出一种自适应的小波配置方法去求解整数阶偏微分方程的初边值问题。他们仅在空间方向即x方向对未知函数进行小波基函数展开,然后在时间方向即t方向利用求解微分方程的时间步进法去求解。由于时间步进法的误差是非均匀分布,误差会随着时间的增加而累积,会产生计算结果的相漂移现象。如果直接用自适应小波配置方法求解分数阶偏微分方程,由于分数阶导数的记忆效应,会导致计算复杂度和计算误差的剧烈增加。
本文中所用的三次样条小波基函数和基函数的分数阶导数的表达式,配置点等,见文献[3].NJ=2JL+3,小波基函数构成的列向量为 ØJ(x)= [ω1(x),…,ωNJ(x )]T.不失一般性,我们考虑带有非齐次源的一维分数阶反常扩散方程:

来近似方程(1)的精确解 u(x,t),其中小波系数 U=(uij)Nt×Nx未知.根据近似公式(2),可得:
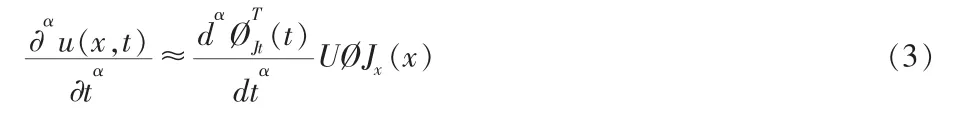

展开系数U可以通过求解广义Sylvester方程(5)-(6)得到,从而方程(1)的近似解可以通过(2)有效的重建。
2 数值例子
本节我们通过两个简单的例子验证这种方法的可行性和有效性。
例1 考虑分数阶偏微分方程

图1分别表示当α=0.1时利用三次样条小波方法求解得到的计算解的绝对误差,这里参数Jx=Jt=3.

图1 例1中解的绝对误差
例2 考虑初边值条件的分数阶偏微分方程

图2表示当α=0.5时利用三次样条小波方法求解得到的计算解的绝对误差,这里参数Jx=Jt=3,图3表示利用文献[2]中的方法得到的计算解的绝对误差。从这些图中我们可以看用小波配置方法得到的计算解的误差要比用有限差分方法得到的结果要小,所以小波配置方法得到的精度高一些。

图2 例2中解的绝对误差
3 结束语
本文我们提出求解分数阶偏微分方程的完全小波配置方法.该方法的主要特点是把分数阶微分方程转化成了一个代数方程。这不仅简化了问题,而且加快了计算速度。数值结果表明该方法是求解分数阶微分方程的一种可行有效的方法。从计算精度上看,如果方程的精确解足够光滑,该方法的结果要比其他方法的好。

图3 文献[2]得到的解的绝对误差
[1]Podlubny I.Fractional differential equations[M].Academic Press,1999.
[2]Gao G,Sun Z,A compact finite difference scheme for the fractional sundiffusion equations[J].Comput.Phys,2011,230:586-95.
[3]Li X,Numerical solution of fractional differential equations using cubic B-spline wavelet collocation method [J].Commun Nonlinear Sci.Numer Simulat,2012,17:3934-3946.
[4]Cai W,Wang JZ,Adaptive multi-resolution collocation methods for initial boundary value problems of nonlinear PDEs[J].SIAM J.Numer.Anal.,1996,33:937-970.
