基于遗传算法的分布式电源选址与定容

2014-04-22汤亚芳

科技视界 2014年24期

薛涛汤亚芳

（贵州大学电气工程学院，贵州贵阳 550025）

0 引言

分布式发电(Distributed Generation，简称DG)是指将发电系统以小规模(发电功率在数千瓦至50MW的小型模块)、分散式的方式布置在用户附近,可独立地输出电能的系统[1]。分布式电源接入配电网，对配电网的节点电压、线路潮流、短路电流、网络可靠性等都会带来影响,其影响程度与分布式电源的位置和容量密切相关。因此，合理的选择分布式电源的位置和容量非常重要[2]。

基于分布式电源对配电网规划的重要影响，本文在分布式电源的位置和容量均不确定的情况下，考虑以配电网网损最小和DG的运行费用最小为目标函数，建立了含分布式电源选址与定容的多目标规划模型[3]，并用遗传算法对分布式电源的位置和容量进行优化，得到分布式电源的优化配置方案。

1 含DG的配电网规划模型

1.1 目标函数

综合考虑分布式电源接入配电网后的网络损耗费用和运行费用，建立归一化数学模型如式（1）所示：

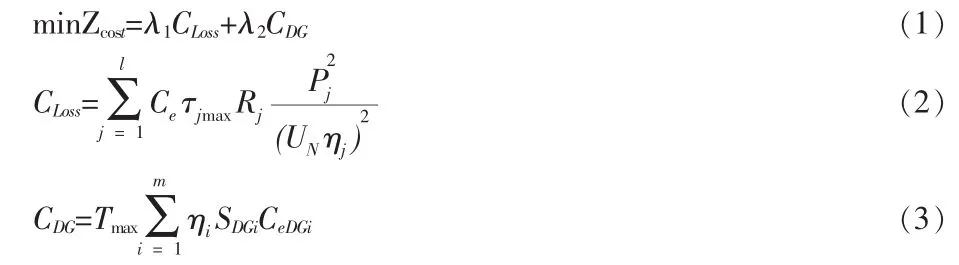
式中：Zcost为总费用，即归一化目标函数；CLoss、CDG分别表示分布式电源接入配电网后的年网络损耗费用、年运行费用，如式（2）、（3）所示，Ce（元/kWh）为单位电价，τjmax为支路j的年最大负荷损耗小时数，Rj为支路j的电阻，Pj为流过支路j的有功功率（kW），UN为线路的额定电压，ηj为线路流过的负荷功率因数，Tmax为分布式电源的最大发电小时数，m为接入配电网的分布式电源的总个数，ηi为分布式电源i的功率因数，SDGi为第i个分布式电源的容量（kVA)，CeDGi为第i个分布式电源的单位电量成本（元/kWh）；λ1、λ2为对应费用的权重系数，0<λ1，λ2<1且 λ1+λ2=1。

1.2 约束条件

（1）节点电压约束条件

Uimin≤Ui≤Uimax

式中，Ui为节点 i的电压；Uimin、Uimax分别为 Ui的上下限。

（2）支路电流不等式约束

Ij≤Ijmax

式中，Ij、Ijmax分别表示第j条支路的电流和允许通过的电流上限。

（3）潮流约束

式中，Pi、Qi分别为节点 i注入的有功和无功功率；Gij、Bij、δij分别为节点 i、j间的电导、电纳和电压相角差；n为系统节点总数；Vi、Vj分别为节点i、j的电压幅值。

2 含DG的配电网潮流计算

接入配电网中的分布式电源所采用的模型，既可以简化成PV节点、也可以是PQ节点，本文将其简化成具有恒定功率因数的PQ节点[4]。由于分布式电源一般靠近负荷中心，所以假设分布式电源的位置在负荷节点上。本文对接入分布式电源的配电网采用前推回代法进行潮流计算[5]，这种潮流计算方法首先假定各节点电压均等于根节点电压，从末端节点开始，由己知的各节点负荷功率、节点电压，向辐射状配电网始端推算各支路的电流以及始端功率。然后由始端向末端推算各节点电压，如此重复以上过程直至迭代收敛为止。

3 分布式电源选址与定容的求解

由于遗传算法具有较好的全局搜索性能、搜索过程不容易陷入局部最优等优点，考虑分布式电源选址定容的特点，本文采用遗传算法求解分布式电源的位置与容量。

3.1 遗传算法

遗传算法[6]是一种模仿生物界自然选择和自然遗传机制的随机搜索算法，它通过某种编码技术，作用于称为染色体的数字串，对由这些串组成的群体的进化过程进行模拟，并通过有组织的、随机的信息交换来重组那些适应性好的串，生成新一代群体。遗传算法以其简单、通用性强、不依赖问题模型等特性，已在函数优化等领域获得广泛应用。

（1）染色体编码

本文对DG的选址定容染色体编码采用实数编码，因此一个允许n个节点安装分布式电源的配电网络，分布式电源的选址定容方案可以用一组变量C={C1，C2，……，Cn}表示，Ci的数值大小表示节点i的分布式电源建设情况，若Ci=0则表示该节点没有安装分布式电源。

（2）遗传操作

遗传算法包括三个基本操作：选择、交叉、变异。通过以适应度函数为依据，对群体进行这三个操作步骤，实现个体之间的信息交换与重组，使群体的适应度不断提高，最终得到全局最优解。本文采用的三种遗传算子如下。

选择算子：选择运算使用比例选择算子来淘汰种群中的劣质个体，保留其中优良个体。选择算子中的选择原理采用比例选择原则，如果假设种群数为M，个体i的适应度为fi，则个体i被选择的概率为：

交叉算子：为了降低优良个体被破坏的可能性，本文在交叉过程中采用动态交叉概率，即设定迭代初期交叉概率值Pc0=0.95，在迭代后期取较小的交叉概率值Pc1=0.45。

变异算子：在变异过程中也采用动态变异概率，设定迭代初期的变异概率值Pm0=0.01，在迭代后期使用较小的变异概率值Pm1=0.001。

（3）算法终止条件

当满足以下两种搜索终止条件的其中一种，则搜索终止：（1）达到最优解连续不变最大代数C；（2）达到遗传操作的终止代数T。

3.2 算法求解流程图

按照上述步骤，设计主函数流程图如图1所示。

图1 主函数流程图

4 算例分析

本文采用IEEE33节点配电系统进行测试，网络结构图如图2所示。假设要在此配电网中建设2个分布式电源，网络中分布式电源待选安装节点编号为2—33，待选单个分布式电源的功率因数取0.9，容量是0.01MVA的整数倍，分布式电源的总装机容量不得超过最大负荷总量的10%，且小于等于所安装节点的负荷量。参数选取如下：种群规模M=30，交叉、变异概率如3.1中所述，年最大负荷利用小时数τj=3000h，单位电价Ce=0.5元/kWh，最优解连续不变最大代数C=5，遗传操作终止代数T=50。

图2 IEEE33节点配电网系统图

取目标函数中的权重系数λ1=0.8，λ2=0.2，遗传操作过程输出的迭代收敛曲线如图3所示（图中红色线表示种群的平均适应度值，黑色线表示最佳适应度值）。

图3 遗传算法迭代曲线

遗传操作后得到的分布式电源位置和容量信息见表1。

表1 DG接入节点

对接入分布式电源与不接入分布式电源的系统费用进行比较，结果见表2。

表2 接入DG与不接入DG费用比较

由以上所得的表1和表2可以看出，含DG的配电网总费用低于不含DG配网的总费用，说明仅考虑DG运行费用和网损费用的情况下，按此方案在这个配电网中接入分布式电源后系统的经济性较好。对接入分布式电源的配电网，网损费用比不接入分布式电源的配电网低，其主要原因是分布式电源接入电网后改善了配电网的潮流分布，从而使系统网损减少。

从图3中的遗传算法迭代曲线可以看出，使用遗传算法对本文目标函数进行优化，种群平均适应度值虽然局部波动比较大，但整体呈下降收敛趋势，表明应用遗传算法对本文目标函数进行优化取得了比较好的效果。