完全二部图Km,n的广播数rn(Km,n)
2014-04-20张晓亮耿显亚刘斌等
张晓亮 耿显亚 刘斌 等
摘要:利用图的顶点之间的距离与多水平标号的最大-最小值原理, 依据顶点排序累积距离最大作为优化多水平距离标号的衡量标准, 证明了完全二部图Km,n的广播数的计算公式rn(Km,n)=m+n。 修正和填补了图的多水平距离标号研究领域的相关问题。另外,图的标号在科学技术和工程领域中有广泛的应用, 同时又是图染色理论的推广, 所以有一定研究价值与应用前景.
关键词:完全二部图; 多水平距离标号; 广播数
中图分类号:O157.5文献标志码:A文章编号:1672-1098(2014)04-0065-03
在无线网络和信号传播途径中, 为了避免不同信号之间的相互干扰而设计不同的广播频率是一项重要的任务。 在信号传播中, 频率相近的信号相互会产生干扰。 这个问题的数学模型可以抽象为图论中点的染色和标号问题, 顶点表示信号发射站, 边表示邻近的信号发射站。 频道设计问题最先由文献[1]提出, 问题的解决先后涉及两水平距离标号, 多水平距离标号。 通常情况下, 两个信号发射站发射的信号之间的干扰程度与两个信号发射站之间的距离有关, 距离越近干扰程度越强。 现假设仅考虑两水平信号干扰, 强调信号干扰与弱调信号干扰。 强干扰发生在非常接近的两个信号发射站, 为了避免干扰, 这两个信号发射站要分两个不同时段发射信号; 弱干扰发生在邻近的信号发射站, 为了避免干扰, 两个信号发射站的信号频道设计不同即可。 作为问题所抽象的数学模型, 利用图论知识构造图G, 图G的顶点代表各自不同的信号发射站, 当两个信号发射站的距离非常接近时, 连接代表它们的顶点作为边。 这样, 不同频道的设计就抽象为图论中道路连接的顶点的标号问题。
广播数就是在不同的信号发射站点设计频道区分标记中的实际用途。 各个站点都标记各自不同的非负整数, 使他们相互之间不受干扰。 广播数的研究就是寻找一种标记方式, 使得在所有可能标记中最大标号最小化。 例如, 研究这种问题的最初模型是两水平标号距离L(2,1), 即寻找
λ(G)=minf max{f(V(G))}, 其中f:V(G)→{0,1,2,…,k}, 满足u,v∈V(G),
|f(u)-f(v)|≥2dist(u,v)=1
1dist(u,v)=2
在经过近十年的研究后, 文献[2]中提出了多水平距离标号模型, 即寻找
rn(G)=minf max{f(V(G))}, 其中f:V(G)→
{0,1,2,…,k},u,v∈V(G),
|f(u)-f(v)|≥diam(G)+1-dist(u,v)
文献[3]给出了在此数学模型下路图Pn和圈图Cn的广播数在n≥3时分别为
rn(Pn)=2k2+2n=2k+1
2k(k-1)+1n=2k
rn(Cn)=n-22φ(n)+1n≡0,2(mod4)
n-12φ(n)n≡1,3(mod4)
其中φ(n)=k+1n=4k+1
k+2n=4k+r,r=0,2,3,在此文中,其定理3关于路图Pn的广播数公式rn(Pn)有小错误,即当n=3时,rn(P3)=3,而非按其公式计算的rn(P3)=4。
本文主要研究完全二部图Km,n的广播数rn(Km,n)。
定理设完全二部图Km,n, 则rn(Km,n)=m+n。
证明根据完全二部图Km,n的特征有, 顶点集合分V(Km,n)=V1∪V2,|V1|=m,|V2|=n,u∈V1,v∈V2,(u,v)∈E(Km,n)。 直径为diam(Km,n)=2, 任意两点间的距离:u,v∈V(Km,n),
dist(u,v)=2u,v∈V1,or,u,v∈V2
1u∈V1,v∈V2,or,u∈V2,v∈V1
距离标号函数f∶V(G)→{0,1,2,…,k}, 满足
|f(u)-f(v)|≥diam(G)+1-dist(u,v)=
3-dist(u,v)=1u,v∈V1,or,u,v∈V2
2u∈V1,v∈V2,or,u∈V2,v∈V1
首先证明rn(Km,n)≥m+n。
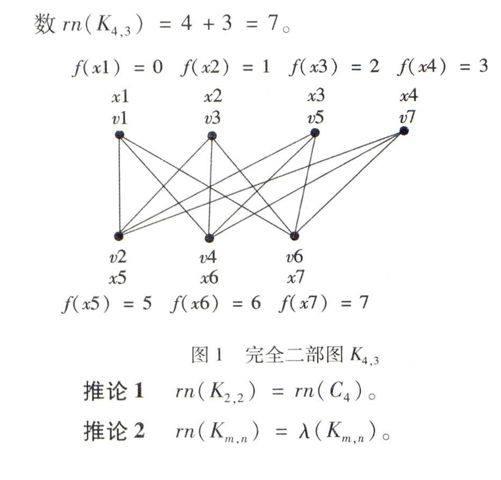
令{x1,x2,…,xm+n}为顶点集合V(Km,n)={v1,v2,…,vm+n}的一个重排,满足条件: f(xi) f(x2)-f(x1)≥3-dist(x2,x1) f(x3)-f(x2)≥3-dist(x3,x2) f(xm+n)-f(xm+n-1)≥3-dist(xm+n,xm+n-1) 以上各式相加得f(xm+n)-f(x1)≥3(m+n-1)-∑m+n-1i=1dist(xi+1,xi),取f(x1)=0即 f(xm+n)≥3(m+n-1)-∑m+n-1i=1dist(xi+1,xi) 另外由dist(u,v)的定义有∑m+n-1i=1dist(xi+1,xi)≤ 2(m-1)+2(n-1)+1=2m+2n-3, 进而f(xm+n)≥ 3(m+n-1)-∑m+n-1i=1dist(xi+1,xi)≥3(m+n-1)-(2m+2n-3)=m+n 所以rn(Km,n)≥m+n。 下面证明rn(Km,n)≤m+n。 令x1,x2,…xm∈V1,xm+1,xm+2,…xm+n∈V2,则有多水平距离标号函数: f(xi+1)=f(xi)+3-dist(xi+1,xi),i=1,2,…,m+n-1 可具体标号如下: f(x1)=0, f(x2)=1, f(x3)=2,…, f(xm)=m-1 f(xm+1)=m+1, f(xm+2)=m+2,…, f(xm+n)=m+n 满足 u,v∈V(G) |f(u)-f(v)|≥diam(G)+1-dist(u,v)=3-dist(u,v) 所以rn(Km,n)≤m+n。 综上所述,rn(Km,n)=m+n。证毕 例如:给出完全二部图K4,3(见图1),其广播数rn(K4,3)=4+3=7。 图1完全二部图K4,3推论1rn(K2,2)=rn(C4)。 推论2rn(Km,n)=λ(Km,n)。 参考文献: [1]W K HALE.Frequency assignment: Theory and applications[J]. Proc. IEEE, 1980 (68):1 497-1 514. [2]DAPHNE DER-FEN LIU, XUDING ZHU.Multilevel Distance Labelings For Paths And Cycles[J]. SIAM J.DISCRETE MATH,2005,19(3):610-621. [3]G CHARTRAND, D ERWIN, P ZHANG.A Graph Labeling Problem Suggested by FM Channel Restrictions[J]. Bull Inst. Combin. Appl, 2005 (43) :43-57. (责任编辑:何学华)