Damage Localization of Marine Risers Using Time Series of Vibration Signals
2014-04-20LIUHaoYANGHezhenandLIUFushun
LIU Hao, YANG Hezhen,, and LIU Fushun
1) State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, P. R. China
2) Department of Ocean Engineering, Ocean University of China, Qingdao 266100, P. R. China
Damage Localization of Marine Risers Using Time Series of Vibration Signals
LIU Hao1), YANG Hezhen1),*, and LIU Fushun2)
1) State Key Laboratory of Ocean Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, P. R. China
2) Department of Ocean Engineering, Ocean University of China, Qingdao 266100, P. R. China
Based on dynamic response signals a damage detection algorithm is developed for marine risers. Damage detection methods based on numerous modal properties have encountered issues in the researches in offshore oil community. For example, significant increase in structure mass due to marine plant/animal growth and changes in modal properties by equipment noise are not the result of damage for riser structures. In an attempt to eliminate the need to determine modal parameters, a data-based method is developed. The implementation of the method requires that vibration data are first standardized to remove the influence of different loading conditions and the autoregressive moving average (ARMA) model is used to fit vibration response signals. In addition, a damage feature factor is introduced based on the autoregressive (AR) parameters. After that, the Euclidean distance between ARMA models is subtracted as a damage indicator for damage detection and localization and a top tensioned riser simulation model with different damage scenarios is analyzed using the proposed method with dynamic acceleration responses of a marine riser as sensor data. Finally, the influence of measured noise is analyzed. According to the damage localization results, the proposed method provides accurate damage locations of risers and is robust to overcome noise effect.
marine risers; structure damage detection; dynamic response; autoregressive moving average model; noise signal
1 Introduction
As oil production industry develops its operation into deep waters, more accurate and reliable damage detection tools for offshore structures are in high demand (Li et al., 2009). One of the most important structural components needed for deep water oil extraction is the slender pipe (riser), which is used to carry oil from the seabed to offshore facilities. Of particular importance is the integrity of the structure since the structural damage of risers may cause total collapse of pipelines or leakage of their internal products, which will have a negative economic and environmental impact (Jacques et al., 2010). Zhang et al. (2012) studied the vibration of marine risers by conducting model tests. Kishawy and Gabbar (2010) provided a review on pipeline integrity and classified the main failures. The marine riser is currently receiving considerable attention in the research community due to its complex dynamic response and the resulting economic impact. Large structural degradation affects the associated structural integrity.
In general, structural damage causes changes in structural stiffness, mass and damping, which alter structural response behavior. Therefore, attempts to monitor the global structural condition and to maintain the structural safety have resulted in the development of the early stage damage identification and the damage-induced collapse prevention. This requires reliable and effective damage identification techniques that offer advantages over taking up the challenges such as those with signal-to-noise ratios, modal identification limitations and modeling errors.
Over the past few decades, miscellaneous vibrationbased methods have been proposed for damage detection and health monitoring in civil, automotive, mechanical and aerospace engineering communities. Two methods are widely used in vibration-based damage detection of structural systems. One is referred to as modal-based, in which the modal parameters are functions of the physical properties of structures. In this regard, Li et al. (2006), Wang and Liu (2010), Yang and Li (2004) gave detailed studies of 3D frame structures, such as offshore platforms. The other method is based on the statistics of measured data and examines the time-histories of the recorded vibration, strain or other data from which information about the changes with the onset of damage can be directly extracted.
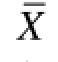
For marine riser structures, time-series based methods offer several advantages over existing modal-based damage methods. First, the time-series based methods utilize response data obtained separately under undamaged and possibly damaged conditions of structures without involving a detailed analytical model of the structures. Second, the modal-based damage detection methods suffer from limitations related to the correct identification of mode shapes. Lastly, modeling errors and modal identification limitations can be avoided in the time-series based approaches.
In this study, a statistical pattern recognition technique is implemented in the riser model and is numerically validated by several damage scenarios. A damage localization index based on coefficients of an ARMA model is proposed. The efficacy is demonstrated using a numerically simulated top tensioned riser (TTR) and the effects of different noise levels are discussed.
2 Theory
2.1 Modeling of Signal Vibration
The mathematical derivation of the model begins with the use of a standardized time series as shown in the following:

Once the initial data are pre-processed, an ARMA(p, q) model with p auto-regressive (AR) terms and q movingaverage (MA) terms is constructed as:

where φk, θkare the kth AR and MA coefficients, respectively, while εij(t) is the residual term.
2.2 Order Determination and Parameter Estimation
Sohn et al. (2003) proposed an AR model using the Yule-Walker method that was later replaced by the Arfit algorithm (Neumaier and Schneider, 2001). This algorithm optimizes the model order selection criteria and computes the model order, popt. A QR factorization of a data matrix is used to evaluate, for a sequence of successive orders, the model order and to compute the parameters of the AR (popt) model that can be represented as follows

Multiplying both sides of Eq. (3) by x(t-k), taking the mean, and defining γ(t)=E[x(t1+t)x(t1)], Eq. (3) can be rewritten as

For k=1, 2, …, p, Eq. (4) becomes

Eq. (5) is called the Yule-Walker formula. The coefficients of (φx1,φx2,…,φxp) can be obtained by matrix inversion.
2.3 Damage Localization Index
In the ARMA model, the first three AR coefficients contain most of the modal frequencies and damping information. After testing several different combinations, it was found that the Euclidean distance of the AR coefficient provides a robust damage localization parameter. Thus the proposed damage sensitivity feature is defined as follows:

where βjis the damage sensitivity feature. The normalized damage index is applied to the damage localization parameter, as shown in Eq. (7) for the purpose of overcoming numerical instability related to small response amplitude.

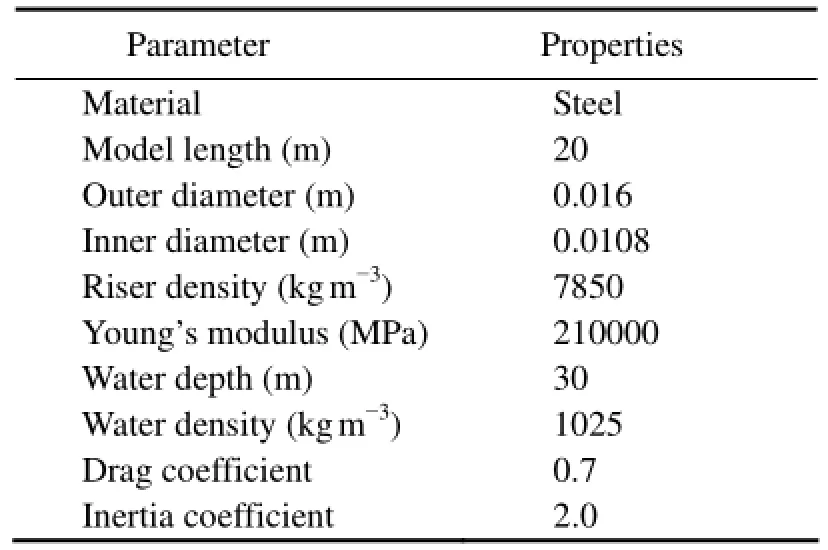
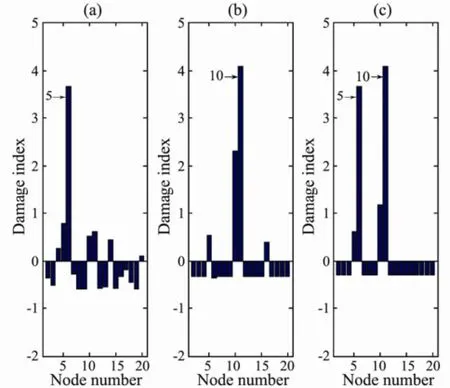
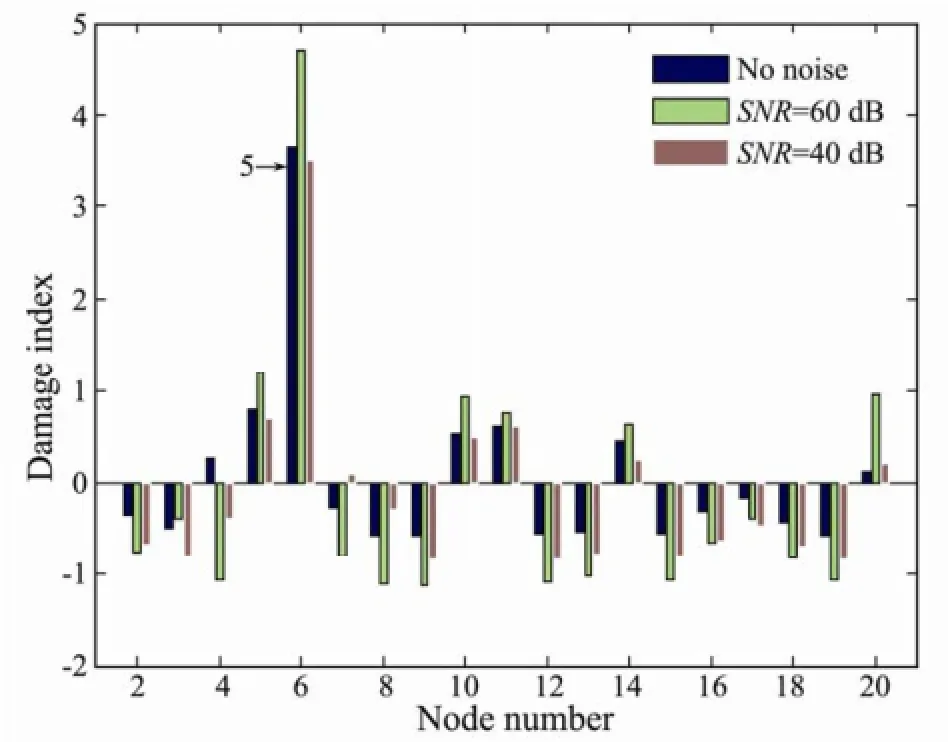
where Zjis the damage localization index and can be used for positioning damage as: i) choose element j as damaged if Zj≥Cr, or ii) choose element j as not damaged if Zj 2.4 Effects of Noise Measurement noise is unavoidable, and will affect the damage detection. The noise intensity can be defined bythe signal-to-noise ratio (SNR), which is often expressed using the logarithmic decibel scale where Ps and Pn are the average powers of signal and noise, respectively. 3.1 Riser Model and Properties Fig.1 shows a sketch of the riser configuration used for this study. The riser was assumed to be a truly vertical one without well offset, idealized as an assembly of 2-node cubic pipe elements using the Euler-Bernoulli beam theory, and discretized to total 20 elements. The element numbers are labeled in order from bottom to top. The properties of the riser model are listed in Table 1. This model is sinusoidally excited along the x-axis with stochastic white-noise at its top end and pinned at its bottom end. The output signal of horizontal acceleration response is obtained from each individual node (a total of 20 nodes except for restrictions). Fig.1 Global TTR model. Table 1 Properties of the riser model 3.2 Damage Scenarios By simplifying the TTR as an Euler-Bernoulli beam in the global model, damages can be simulated by reducing the stiffness of short elements located in sensor regions. Many researchers used this method to simulate damage cases (Liu et al., 2007). In this study, damage scenarios are designed, and three proposed damage cases and the corresponding locations of stiffness-reduced elements are shown in Table 2. Table 2 Damage scenarios 4.1 Time Series Modeling of Measured Data The main steps are as follows: 1) generate and normalize signals at each node position of the healthy TTR structure; 2) obtain and normalize signals from the damaged structures; 3) construct ARMA models for each data channel; 4) calculate damage indexes for each sensor; 5) discuss the effects of measurement noise. Fig.2 shows the vibration signal at node 2 of an undamaged case. It is necessary to perform standardization of all data streams according to Eq. (1), after which the statistical features of all undamaged cases can be readily compared. Fig.3 shows the autocorrelation function (ACF) of the standardized data. The moving average is used to remove the periodic trend of the data. The optimum ARMA model order and its coefficients can be estimated once the initial data pre-processing is completed. Fig.4 shows the shift of the AIC values with the AR prediction model order. It can be seen that the orders 3–5 are appropriate for the analysis. For each data channel, the dataset is divided into two, one is used for the analysis and the other is used for model prediction and validation. The time prediction model is established based on the selected reference signal. Fig.5 shows that the model well reproduces the measured signal. Fig.2 Acceleration time history of an undamaged case. Fig.3 Autocorrelation function of the normalized data. Fig.4 Variation of Akaike information criteria (AIC) with model order. Fig.5 Comparison between measured and predicted signals. 4.2 Damage Localization Results The ARMA model is implemented for all signals. The damage localization index is then used to locate the damage. The simulation results for the damage scenarios are shown in Fig.6. It can be seen from Fig.6 that there is a significant difference between the values in damaged and undamaged regions. For damage scenarios 1 to 3, the stiffness- reduced elements have the indexes greater than one. Especially for scenario 3 two nonadjacent damaged elements correspond to the two peaks in the damage locations. It is shown that the AR coefficients are related to the mechanical system, which indicates a close correlation between stiffness and AR coefficients. In practice, all measurements contain noise, detrimentally affecting the technique. In order to verify the proposed algorithm in actual test environment, it is necessary to consider the effects of noise. Here the signal noise ratios of 60dB and 40dB are added to various test conditions. Damage localization results under measured noise are shown for damage scenarios 1 and 3 in Figs.7 and 8, respectively. From the normalized DI values in Fig.7, it can be concluded that this method is able to locate damages using measurements with noise. Fig.6 Damage localization index. (a) ID1, (b) ID2, (c) ID3. Fig.7 Damage localization index with noise (ID1 with SNR=60 dB, 40 dB). For the damage scenario 3, the DIs accurately locate the damages of elements 5 and 10. Similarly, damage localization results with measurement noise show twocorresponding peaks at the actual damage location (Fig.8). However, as the level of noise increases, the damage indicator becomes weaker. The maximum value of the normalized DI is about 4.09 for no measurement noise, and 3.6 and 2.85 for SNR=60dB and 40dB at Node 11 of Element 10, respectively. The results obtained above from ARMA model parameters demonstrate good performance of this damage detection method. Fig.8 Damage localization index with noise (ID3 with SNR=60 dB, 40 dB). Based on the ARMA model of marine risers, a new structural damage detection scheme is presented. Dynamic response records are collected from the undamaged and reference-state structure. A localization index defined by auto-regression coefficients in the ARMA model is introduced. The efficiency of the proposed framework is demonstrated by the numerical study of a TTR riser. Using the calculated results the effects of the signal-to-noise levels of 60dB and 40dB are discussed. Conclusions are drawn as follows: 1) The vibration response predicted by the ARMA model agrees well with the measurements. 2) The proposed method is effective in the (multiple) damage localization on marine riser structure. 3) The damage localization index is accurate under a small SNR ratio. This research was financially supported by the 973 Project (Grant No. 2011CB013704) and by the National Natural Science Foundation of China (Grant Nos. 51379005, 51009093). Bao, C., Hao, H., and Li, Z. X., 2013. Integrated ARMA model method for damage detection of subsea pipeline system. Engineering Structures, 48: 176-192. Brincker, R., Kirkegaard, P. H., Andersen, P., and Martinez, M., 1995. Damage detection in an offshore structure. In: The 13th International Modal Analysis Conference (IMAC XIII). Spie International Society for Optical, 661-667. De Lautour, O. R., and Omenzetter, P., 2010. Nearest neighbor and learning vector quantization classification for damage detection using time series analysis. Structural Control and Health Monitoring, 17: 614-631. Jacques, R., Clarke, T., Morikawa, S., and Strohaecker, T., 2010. Monitoring the structural integrity of a flexible riser during dynamic loading with a combination of non-destructive testing methods. NDT & E International, 43: 501-506. Kishawy, H. A., and Gabbar, H. A., 2010. Review of pipeline integrity management practices. International Journal of Pressure Vessels and Piping, 87: 373-380. Li, H. J., Yang, H. Z., and Hu, S. J., 2006. Modal strain energy decomposition method for damage localization in 3D frame structures. Journal of Engineering Mechanics, 132: 941-951. Li, H. J., Zhang, M., Wang, J. R., and James, H., 2009. Fundamental modeling issues on benchmark structure for structural health monitoring. Science in China Series E: Technological Sciences, 52: 1999-2008. Liu, F., Li, H. J., Yu, G., Zhang, Y., Wang, W., and Sun, W., 2007. New damage-locating method for bridges subjected to a moving load. Journal of Ocean University of China, 6: 199-204. Lynch, J. P., Sundararajan, A., Law, K. H., Kiremidjian, A. S., and Carryer, E., 2004. Embedding damage detection algorithms in a wireless sensing unit for operational power efficiency. Smart Materials and Structures, 13: 800-809. Nair, K. K., Kiremidjian, A. S., and Law, K. H., 2006. Time series-based damage detection and localization algorithm with application to the ASCE benchmark structure. Journal of Sound and Vibration, 291: 349-368. Neumaier, A., and Schneider, T., 2001. Estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Transactions on Mathematical Software (TOMS), 27: 27-57. Sohn, H., Allen, D. W., Worden, K., and Farrar, C. R., 2003. Statistical damage classification using sequential probability ratio tests. Structural Health Monitoring, 2: 57-74. Sohn, H., and Farrar, C. R., 2001. Damage diagnosis using time series analysis of vibration signals. Smart Materials and Structures, 10: 446-452. Sohn, H., Czarnecki, J. A., and Farrar, C. R., 2000. Structural health monitoring using statistical process control. Journal of Structural Engineering, 126: 1356-1363. Wang, S. Q., and Liu, F. S., 2010. New accuracy indicator to quantify the true and false modes for eigensystem realization algorithm. Structural Engineering and Mechanics, 34: 625-634. Wei, Z., Yam, L. H., and Cheng, L., 2005. NARMAX model representation and its application to damage detection for multi-layer composites. Composite Structures, 68: 109-117. Yang, H. Z., and Li, H. J., 2004. Modal parameter identification of offshore platforms under ambient excitation. High Technology Letters, 10: 80-84. Zhang, Y. B., Guo, H. Y., Liu, X. C., and Li, X. M., 2012. Investigation of a new vortex-induced vibration suppression device in laboratory experiments. Journal of Ocean University of China, 11: 129-136. (Edited by Xie Jun) (Received December 25, 2012; revised May 2, 2013; accepted June 4, 2014) © Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2014 * Corresponding author. E-mail: yanghz@sjtu.edu.cn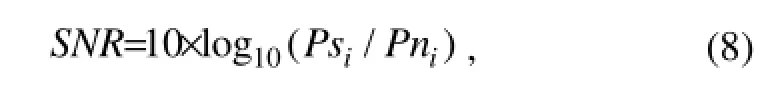
3 Simulation Case Study


4 Results and Discussion





5 Conclusions
Acknowledgements
杂志排行
Journal of Ocean University of China的其它文章
- Sedimentary Evolution of the Holocene Subaqueous Clinoform off the Southern Shandong Peninsula in the Western South Yellow Sea
- Identification of Fucans from Four Species of Sea Cucumber by High Temperature1H NMR
- Experimental Study on the Flow Around Two Tandem Cylinders with Unequal Diameters
- Revision of P-wave Velocity and Thickness of Hydrate Layer in Shenhu Area, South China Sea
- Study on Internal Waves Generated by Tidal Flow over Critical Topography
- Isolation and Characterization of Fucoidans from Five Brown Algae and Evaluation of Their Antioxidant Activity
