Experimental Study on the Flow Around Two Tandem Cylinders with Unequal Diameters

GAO Yangyang, ETIENNE Stephane, WANG Xikun, and TAN Soon Keat

1) Ocean College, Zhejiang University, Hangzhou 310058, P. R. China

2) State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, SOA, Hangzhou 310012, P. R. China

3) Mechanical Engineering Department, Ecole Polytechnique de Montreal, H3C 3A7, Canada

4) Maritime Research Centre and School of Civil and Environmental Engineering, Nanyang Technological University, 6397898, Singapore

Experimental Study on the Flow Around Two Tandem Cylinders with Unequal Diameters

GAO Yangyang1),2),*, ETIENNE Stephane3), WANG Xikun4), and TAN Soon Keat4)

1) Ocean College, Zhejiang University, Hangzhou 310058, P. R. China

2) State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, SOA, Hangzhou 310012, P. R. China

3) Mechanical Engineering Department, Ecole Polytechnique de Montreal, H3C 3A7, Canada

4) Maritime Research Centre and School of Civil and Environmental Engineering, Nanyang Technological University, 6397898, Singapore

In this paper, flow around two circular cylinders in tandem arrangement with unequal diameters has been investigated using the particle image velocimetry technique (PIV) in a water channel. The upstream to downstream diameter ratio was kept constant at d/D=2/3, the centre-to-centre distance was varied from 1.2D to 5D and the Reynolds number was varied from 1200 to 4800. The flow characteristics were analyzed through ensemble-averaged patterns of velocity, vorticity, normalized Reynolds stress contours and streamlines. Based on ensemble-averaged and instantaneous flow fields, different flow patterns, including single-wakeshedding at small spacing ratio, bi-stable flow behavior (alternating behavior of reattachment and vortex shedding) at intermediate spacing ratio and co-shedding pattern at large spacing ratio were observed. The effects of Reynolds number and the centre-to-centre spacing ratio on flow patterns and turbulent characteristics were also investigated. It was found that the diameter ratio appears to have a certain effect on the flow patterns at intermediate spacing ratios, where the reattachment of shear layer depends on the lateral width of the wake flow in the lee of the upstream cylinder. Extensive discussion on the distributions of Reynolds stress and turbulent kinetic energy was presented.

tandem cylinders with unequal diameters; PIV; flow patterns; Reynolds stress distribution

1 Introduction

It is well known that two circular cylinders in tandem configurations are prevalent in engineering applications, such as offshore platforms, tube bundles in heat exchangers, bridge piers and chimney stacks. Most of the investigations of the tandem configurations refer to two cylinders of equal diameter based on Zdravkovich (1987)’s classification (for example, Mittal et al., 1997; Lin et al., 2002; Alam et al., 2003; Xu and Zhou, 2004; Carmo and Meneghini, 2006). Three regimes have been identified based on the behavior of the spacing ratio L/D (L is the distance between centers of the cylinders and D is the cylinder diameter): i) a single bluff body and the shear layers separated from the front cylinder do not reattach onto the surface of the second cylinder; ii) the shear layers separated from the front cylinder reattach onto the surface of the second cylinder and vortex shedding occurs only in the wake of the second cylinder; iii) vortex- shedding occurs both in the gap between the cylinders and behind the second cylinder.

Two main experimental approaches have been reported for measurements of flow around two tandem cylinders with equal diameter. The first approach is focused on vortex shedding frequencies, dynamic pressure and lift and drag coefficients using hot-wire and load cell measurement techniques (Ljungkrona et al., 1991; Ljungkrona and Sunden, 1993; Xu and Zhou, 2004). Ljungkrona et al. (1991) investigated the effect of the free-stream turbulence intensity on the critical spacing ratio by examining the pressure fluctuations on the surfaces of two tandem cylinders of equal diameter, and reported the spacing ratio at which the shear layers separated from the upstream cylinder no longer reattach onto the surface of the downstream cylinder (instead, Karman vortex shedding occurs at the gap between two cylinders). Zhou and Yiu (2006) investigated the flow structure, momentum and heat transport in the wake of two tandem cylinders using a three-wire probe, in conjunction with a cross-wire. They found that in the reattachment regime, two different flow structures were observed depending on whether the shear layers from the upstream cylinder reattach on the down-stream or upstream side of the downstream cylinder.

The second approach is focused on the flow patterns to understand the flow dynamics using flow visualization and the particle image velocimetry technique (Ljungkrona and Sunden, 1993; Sumner et al., 1999, 2000; Lin et al., 2002). Ljungkrona and Sunden (1993) studied the effect of Reynolds number on the dimensionless cylinder spacing. Lin et al. (2002) investigated the instantaneous and averaged flow structures over two tandem cylinders using the particle image velocimetry technique (PIV). They obtained some qualitative results on different flow patterns varying with spacing ratios. The experimental and numerical investigations on the flow around two infinite circular cylinders of equal diameters arranged in different configurations are reviewed by Sumner (2010). For two tandem cylinders, the classification of flow patterns, Reynolds number effects, measurements of fluid forces and vortex shedding frequencies and other parameters have been summarized.

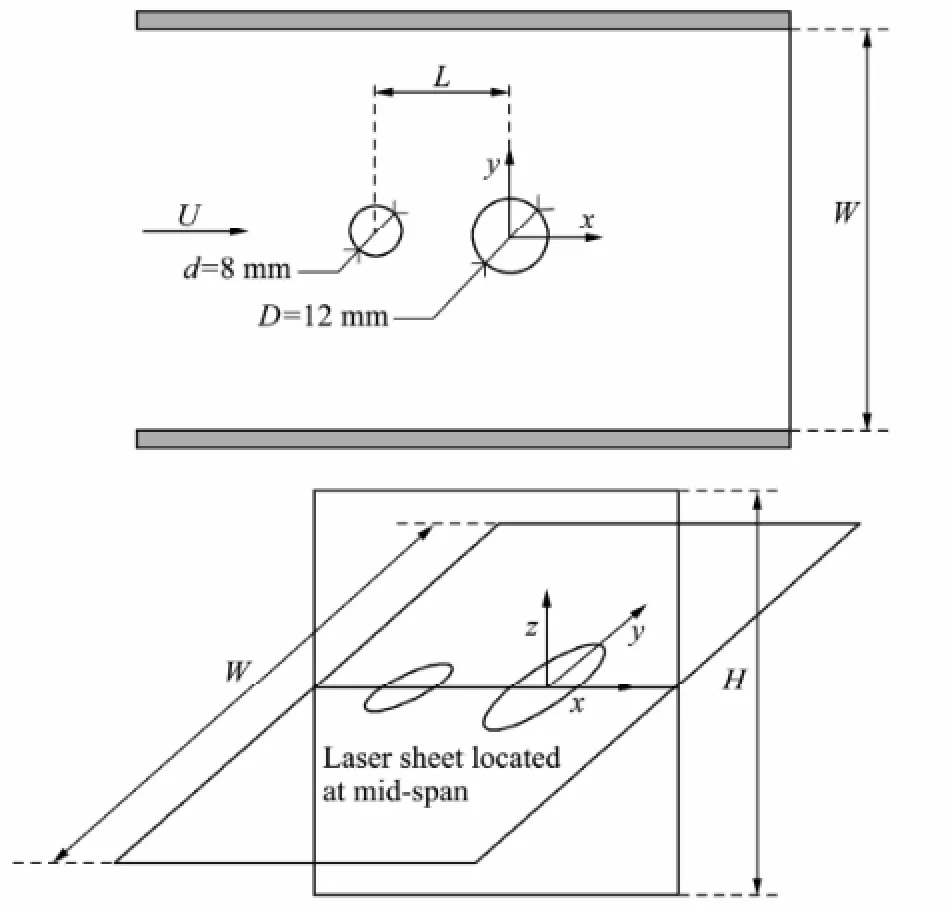
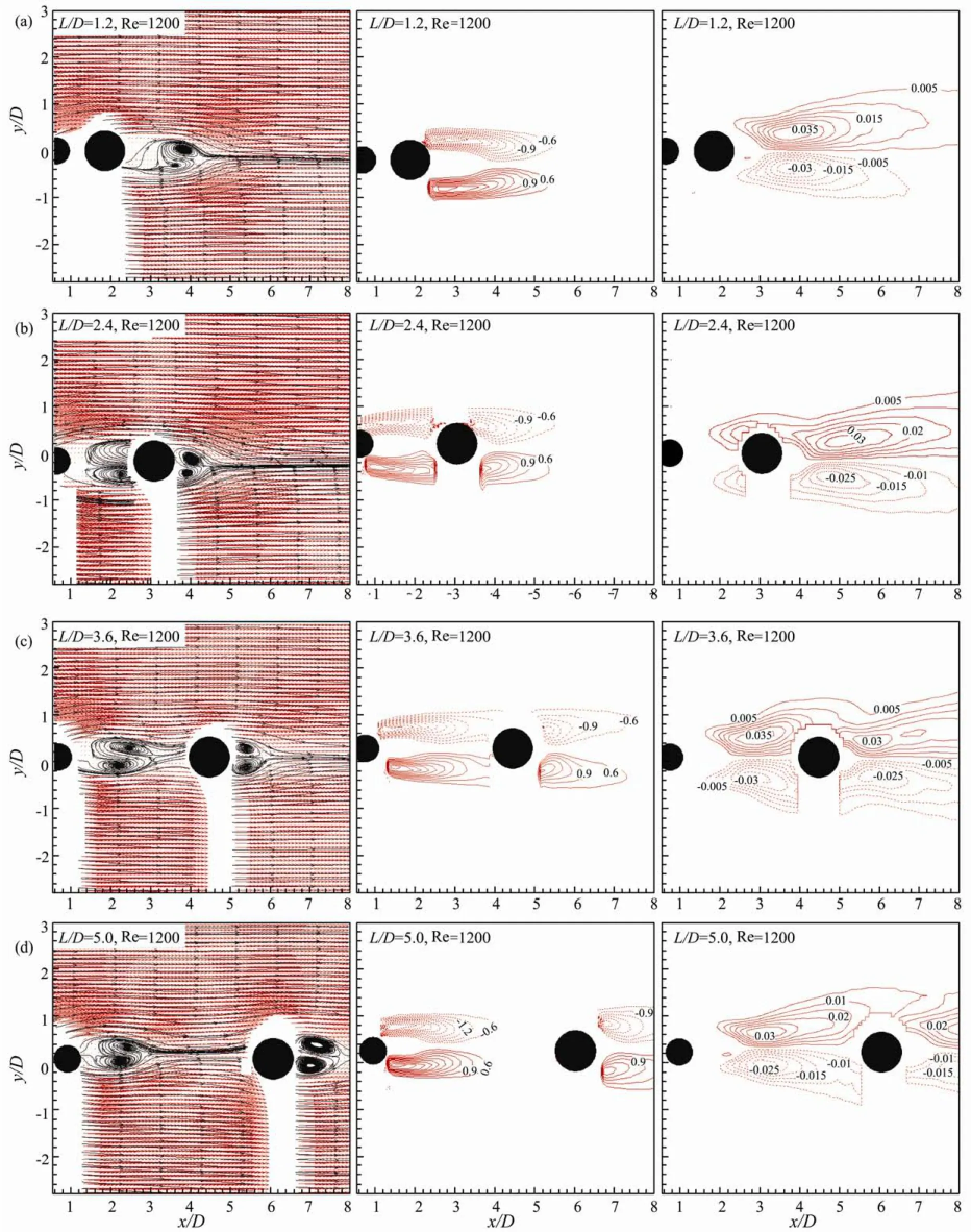
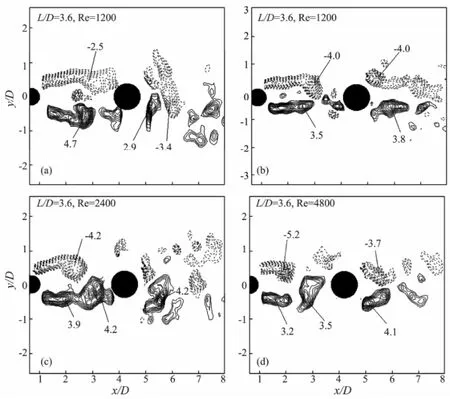
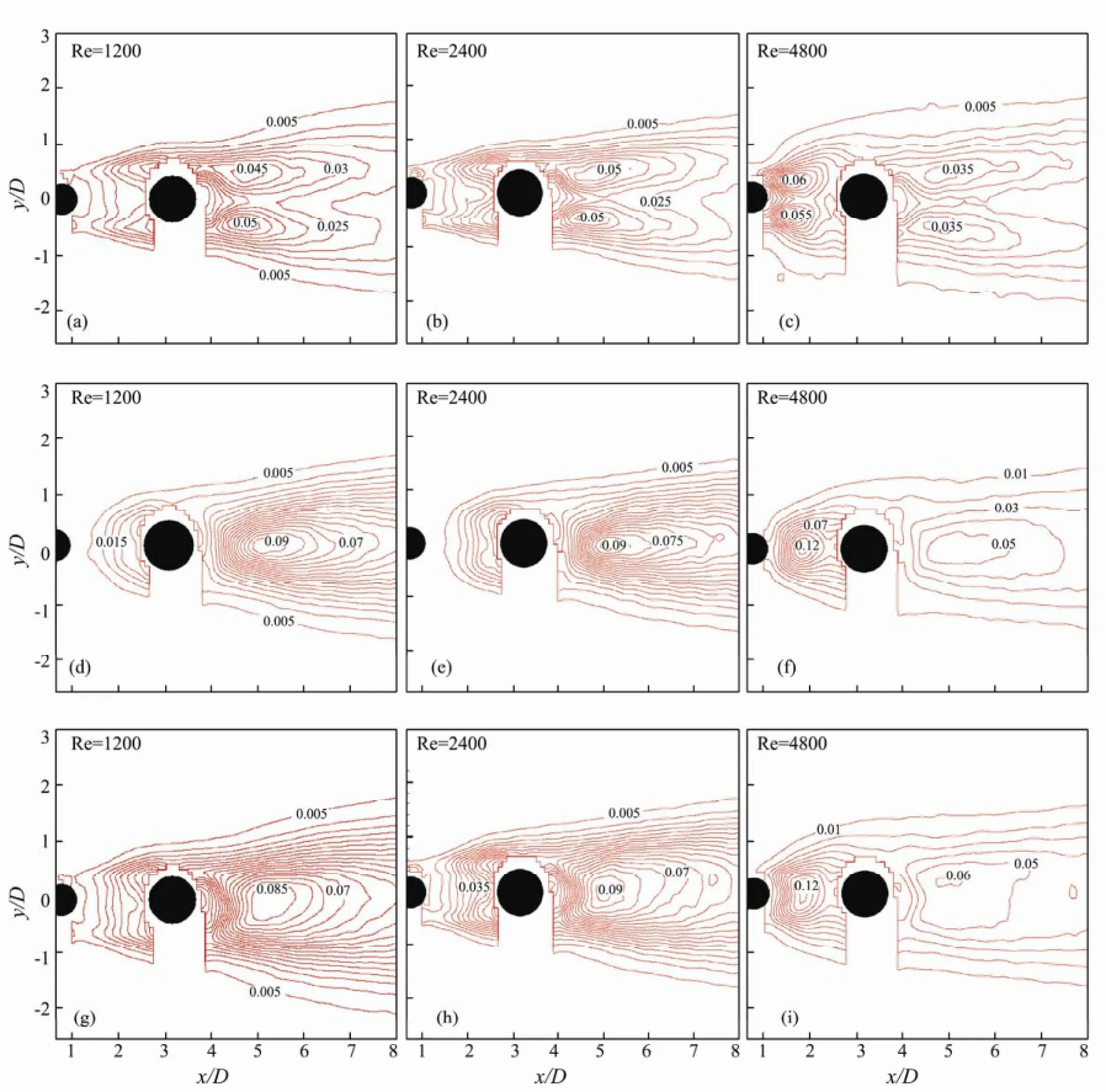
Numerical simulations of the flow around two tandem circular cylinders with equal diameter have been investigated by several authors. Meneghini et al. (2001) investigated the flow around two circular cylinders in tandem and side-by-side arrangements at Re=100 and 200 using a 2D finite-element method (FEM). They obtained flow configuration regimes as defined by Zdravkovich (1977) in the range of experimental results. Jester and Kallinderis (2003) also studied the flow around two circular cylinders in various arrangements using the 2D FEM and found that hysteretic effects exist for 2

As mentioned above, bundled cylinders are widely used at offshore platform, bridge piers and tube bundles in heat exchangers, to name a few engineering applications. Depending on the spacing ratio L/D, bundled cylinders with equal diameter have been found to act as a single bluff body in the flow or experience different states of vortex shedding between and behind these cylinders. Only a handful of studies have been reported on the flow characteristics behind two circular cylinders with unequal diameters in tandem arrangement. Considering the case when bundled cylinders are with unequal diameters, such as piggyback pipeline commonly found in the offshore oil and gas industry, what will happen to them if they are arranged with different spacing ratios? What kind of flow behaviors will appear around the bundled cylinders? These questions are still unanswered fully today.

Igarashi (1982) reported experiments of flow around two cylinders arranged in tandem with the larger diameter cylinder located upstream. Igarashi’s results indicated three regimes with co-shedding occurring for spacing ratios higher than a critical spacing (between 2 and 2.5), which is lower than in the equal diameter cylinder cases. While with a smaller diameter cylinder located upstream, Gao et al. (2011) found that depending on the initial perturbations, the occurring range for bi-stable phenomenon increases with the diameter ratio of downstream to upstream cylinder. To investigate the effect of a small cylinder on the forces on a large downstream cylinder, Alam and Zhou (2008) investigated the variation of flow structures, Strouhal number, time-averaged and fluctuating forces on the downstream cylinder with decreasing of d/D (where D is the downstream cylinder diameter and d is the upstream cylinder diameter) in the co-shedding regime. Moreover, a number of reported studies considered the effects of placing a small (control) circular cylinder behind a large (main) cylinder in tandem configuration. It was shown that either the vortex shedding from the main cylinder (Strykowski and Sreenivasan, 1990; Mittal and Raghuvanshi, 2001) or its lift (Dalton et al., 2001) could be suppressed with appropriate placement of the control cylinder. Furthermore, Zhao et al. (2005, 2007) found that the relative position of the small cylinder has a significant effect on both vortex shedding and hydrodynamic forces with the main cylinder.

In this study, the flow behavior behind two circular cylinders of different diameters arranged in tandem was investigated using the PIV system, for which the larger diameter cylinder is located downstream. The flow characteristics were analyzed through ensemble-averaged and instantaneous flow fields, and Reynolds stress distributions for center-to-center spacing ratios in the range of 1.2 to 5.0.

2 Experiment Set-Up

The experiments were conducted in a 6 m long, re- circulating open water channel at the Maritime Research Centre, Nanyang Technological University. The test section was a rectangular cross-section of 0.3 m×0.4 m (W×H). A schematic sketch of the experimental system is shown in Fig.1, where L is the center-to-center distance and the coordinates x, y and z denote the streamwise, transverse, and spanwise directions, respectively.

Two steel cylinders with 12mm and 8mm diameters were mounted vertically in the y-z plane (x=0), perpendicular to the oncoming flow in the x direction. The aspects ratios of the two cylinders are 16.7 and 25, respectively for the large and small cylinders. To make sure that the cylinders were aligned in tandem and parallel to one another, the two cylinders were fixed and supported at the top end through precisely machined top plate with a carefully aligned 12 mm and 8 mm pair of openings in the longitudinal axis, through which the cylinders were inserted. The cylinders protruded through the top plate and were secured such that they were normal to the plate. The plate was positioned horizontally in the channel and lev-eled with the aid of a spirit level. To ensure that it was horizontal, the laser sheet was first aligned horizontally against the surface of still water in the channel and then lowered vertically with the traversing unit to the desired elevation and plane of measurement. The settling chamber upstream of the contraction was fitted with perforated plates and honeycomb-screen to ensure uniformity of the flow into the test section.

Fig.1 A schematic sketch of the experimental system .

Measurements were conducted using a PIV system (Lavision model). Based on a compromise between the requirements of recording a large field of view and resolving detailed flow structures, the viewing area was chosen to be about 125 mm×95 mm. A Quantel System double cavity Nd: YAG laser (power ～120 mJ per pulse, duration ～5 ns) was used to illuminate the flow field. The particle images were recorded using a 12-bit charge- coupled device (CCD) camera, which has a resolution of 1600×1200 pixels and a frame rate of 15 Hz.

The LaVision Davis software was used to process the raw particle images and determine the flow vector fields. Velocity vectors were determined using the FFT (Fast-Fourier-Transform) method based on cross correlation algorithm with the standard Gaussian sub-pixel fit structured as an iterative multi-grid method. The processing procedure included two passes, starting with a grid size of 64×64 pixels, stepping down to 32×32 pixels overlapping by 50%. A set of 7500 vectors was obtained in the viewing area. For each case, a set of 1050 frames of the instantaneous flow fields was acquired (i.e., 70 s recordings). Details of the PIV measurement system and the accuracy of velocity measurement are described in Gao et al. (2013).

The free-stream velocity was obtained as the mean velocity in this experiment, with values of U0=0.1, 0.2, 0.4 m s-1. The corresponding Reynolds numbers Re=U0D/υ were 1200, 2400, 4800 (where D is the larger cylinder diameter, U0is the free-stream velocity and υ is the kinematic viscosity).

3 Results and Discussion

Flow patterns behind the two tandem cylinders with unequal diameters can be deduced from the velocity flow fields, streamlines topologies, vorticity contours and normalized Reynolds stress contours, as captured by the PIV technique.

3.1 Ensemble-Averaged Wake Characteristics

As shown in Fig.2, the Reynolds shear stress contours for L/D=1.2 are asymmetric about the longitudinal axis in the lee of downstream cylinder, where the peak value of the positive Reynolds stress contours is distinctly larger than its negative counterpart. Vortex street is only observed behind the downstream cylinder; the two cylinders appear to behave as a single bluff body.

At L/D=2.4, two recirculation zones enclosed by the shear layers can be observed behind both cylinders, with two incomplete elliptical-shape vortices in the lee of the upstream smaller cylinder and two smaller but complete ellipses of streamlines in the lee of the downstream and larger cylinder. Evidently the presence of the larger cylinder has constrained the streamwise growth of recirculation region in the lee of smaller upstream cylinder. Furthermore, it can be seen from the vorticity contours that two shear layers are formed in the wake of the upstream cylinder merged into the vortex shed from the downstream cylinder. Normalized Reynolds shear stress at this L/D shows that the main flow contours are located in the lee of the larger downstream cylinder. Similar to that for L/D=1.2, the peak value of positive Reynolds shear stress is larger than that of the negative counterpart.

With a larger spacing ratio L/D=3.6, two ellipticalshape vortices can be observed in the lee of the upstream cylinder and two smaller ones in the lee of the downstream and larger cylinder. Reattachment of the shear layers emanating from the upstream cylinder to that from the downstream cylinder is also observed in this case. The normalized Reynolds stress contours maxima are displaced to a more upstream location of the larger downstream cylinder.

At larger L/D =5.0, two elliptical-shape vortices are formed in the lee of the upstream cylinder and two smaller ones formed behind the downstream cylinder. In this regime, two complete vortex streets are generated from both cylinders, which appear to be independent ofeach other. These results are in accordance with Zdravkovich’s regime identification (Zdravkovich, 1977, 1987).

Fig.2 Ensemble-averaged velocity vector, streamline, vorticity contours ω*=ωzD/U0and normalized Reynolds shear stress fields for the two tandem cylinders with different diameters in the steady cross-flow (from left to right). For Re=1200 (a) L/D=1.2; (b) L/D=2.4; (c) L/D=3.6; (d) L/D=5.0 (from up to down). Solid and dashed lines represent respectively positive and negative. Incremental value of vorticity is 0.3; Reynolds shear stresscontour interval is 0.005.

Fig.3 Lateral distribution of the ensemble-averaged streamwise velocity and root mean square velocity at different locations behind the larger cylinder for different spacing ratios at Re=1200.

3.2 Instantaneous Wake Characteristics

Instantaneous vorticity contours behind two circular cylinders of different diameters in tandem are shown in Figs.4, 5, 6 and 7, for L/D=1.2, 2.4, 3.6 and 5.0 respectively. In these figures, solid lines represent positive values and dashed lines represent negative values. Incremental value of vorticity contour ω*=ωzD/U0is equal to 0.3 and the maximum positive and negative values are marked in these figures, in which the spanwise vorticity ωzis calculated using the least squares extrapolation scheme, as ωz=∂v/∂x-∂u/∂y.

It can be seen from Fig.4 for L/D=1.2 that the cylinder pair behaves like a single bluff body and vortex shedding is observed behind the larger cylinder at different Reynolds numbers. However, no instantaneous wake characteristics from the smaller cylinder are observed in the gap between the cylinders due to the shadow cast.

For L/D=2.4, there is sufficient clearance for vortices to be formed (see Fig.5). Note that, for flow over equaldiameter circular cylinders in tandem configuration, bistable flow phenomena have been observed and reported (Igarashi, 1982, 1984; Strykowski and Sreenivasan, 1990; Dalton et al., 2001; Xu and Zhou, 2004; Alam and Zhou, 2008). From Figs.5(a) and (b), for the same Reynolds number Re=1200, bi-stable flow patterns are observed at the same L/D. The shear layers reattach onto the surface of the larger cylinder as shown in Fig.5(a) or split and generate small-scale vortices behind the upstream cylinder as shown in Fig.5(b).

Different from the case of equal diameters, the lateral width of the wake flow in the lee of the upstream cylinder exerts a certain influence on the flow patterns. Since the smaller cylinder is located upstream, the lateral width of the wake in the gap between two cylinders must be larger than the diameter of the downstream cylinder to ensure the occurrence of reattachment, that is, the shear layers separated from the upstream cylinder will reattach ontothe surface of the larger cylinder. Otherwise, the shear layers generated from the upstream cylinder will alternately impinge on the surface of the downstream cylinder, and then cascade into smaller vortices.

Fig.4 Instantaneous vorticity contours for the case of L/D=1.2.

Fig.5 Instantaneous vorticity contours for the case of L/D=2.4.

As shown in Fig.6, for L/D=3.6, because of the disturbance of vortices shed from the upstream cylinder, irregular shear layers are formed behind the downstream cylinder. On the other hand, the downstream cylinder also has an effect on the vortices shed from the upstream cylinder, consistent with the conclusion obtained by Bearman and Wadcock (1973) and Xu and Zhou (2004), which stated that ‘the presence of the downstream cylinder affects the vortices shed from the upstream cylinder, which subsequently feeds back and influences the instabilities of the shear layers around the upstream cylinder’. Similar to the case of equal diameter cylinders, alternating reattachment occurs, as shown in Fig.6(a). Coshedding in the lee of the two cylinders can be seen in Fig.6(b), which indicates that the flow is bi-stable at the same Reynolds number Re=1200.

As shown in Fig.6(c), when Re=2400, the convected shear layers generated by the upstream cylinder seem similar to those at Re=1200, reattach on the downstream cylinder alternately. Conversely, at Re=4800, there are definite vortices with opposite-sign in the gap between cylinders; both cylinders shed vortices in Fig.6(d). Because of the disturbance of vortices shed from the upstream cylinder, the shear layers behind the downstream cylinder gradually become irregular. They begin to swirl and distort themselves. The downstream cylinder also affects the vortices shed from the upstream cylinder, which subsequently feeds back and influences the instabilities of the shear layers around the upstream cylinder (Bearman and Wadcock, 1973).

From the three PIV snapshots as shown in Fig.7, for L/D=5.0, vortices are generated and shed from both cylinders. The vortices shed from the smaller cylinder deform as they impinge on the larger cylinder and do not appear to influence the vortex shedding in the lee of the downstream cylinder.

Fig.6 Instantaneous vorticity contours for the case of L/D=3.6.

Fig.7 Instantaneous vorticity contours for the case of L/D=5.0.

3.3 Reynolds Stress Profiles

Above all, it can be concluded that from the view of the distributions of Reynolds stress contours and turbulent kinetic energy, different flow characteristics can be observed when varying L/D at the rear of the cylinder-pair. This provides another evidence of the flow behaviors.

Fig.8 Contours of Reynolds normal stress(b, e, h, k) and turbulent kinetic energy(c, f, i, l) for the tandem cylinders at different L/D with Re=1200.

Fig.9 Contours of Reynolds normal stressesand turbulent kinetic energy(g, h, i) for the tandem cylinders at L/D=2.4 with different Reynolds numbers.

4 Conclusions

Flow patterns behind two circular cylinders of unequal diameters in tandem arrangement were investigated using PIV technique. The conclusions include the following:

1) Three flow-pattern regimes including a single bluff body, alternating behavior of reattachment and vortex shedding and independent vortex shedding behavior at various spacing ratios have been identified. Different from the case of equal diameter, the diameter ratio presents certain influence on the flow patterns at intermediate spacing ratios L/D=2.4 and L/D=3.6, where the occurrence of shear layers reattachment depends on the lateral width of the wake flow in the lee of the upstream cylinder.

2) With the increasing of spacing ratio, different scales of Reynolds stress contours from the upstream smaller cylinder, including the case of increasing Reynolds numbers can be observed. This observation provides another evidence of the various flow patterns observed when varying L/D at the rear of the cylinder-pair.

Acknowledgements

The research was supported by the Zhejiang Provincial Natural Science Foundation of China under Grant No. LY14E090009, State Key Laboratory of Satellite Ocean Environment Dynamics (Second Institute of Oceanography, SOA), State Key Laboratory of Fluid Power Transmission and Control (GZKF-201310), State Key Laboratory of Ocean Engineering, China. The National Research Foundation of Singapore (NRF-CRP5-2009-01), Maritime Research Centre and Nanyang Environment and Water Research Institute, Nanyang Technological University, Singapore, is acknowledged.

Alam, M. M., and Zhou, Y., 2008. Strouhal numbers, forces and flow structures around two tandem cylinders of different di-ameters. Journal of Fluids and Structures, 24: 505-526.

Alam, M., Moriya, M., Takai, K., and Sakamoto, H., 2003. Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number. Journal of Wind Engineering and Industrial Aerodynamics, 91: 139-154.

Bearman, P. W., and Wadcock, A. J., 1973. The interaction between a pair of circular cylinder normal to a stream. Journal of Fluid Mechanics, 61: 499-511.

Carmo, B. S., Meneghini, J. R., and Sherwin, S. J., 2010a. Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing. Physics of Fluids, 22, 054101.

Carmo, B. S., Meneghini, J. R., and Sherwin, S. J., 2010b. Secondary instabilities in the flow around two circular cylinders in tandem. Journal of Fluid Mechanics, 644: 395-431.

Carmo, B., and Meneghini, J., 2006. Numerical investigation of the flow around two circular cylinders in tandem. Journal of Fluids and Structures, 22: 979-988.

Dalton, C., Xu, Y., and Owen, J. C., 2001. The suppression of lift on a circular cylinder due to vortex shedding at moderate Reynolds numbers. Journal of Fluids and Structures, 15: 617-628.

Gao, Y. Y., Etienne, S., Yu, D. Y., Wang, X. K., and Tan, S. K., 2011. Bi-stable flow around tandem cylinders of different diameters at low Reynolds number. Fluid Dynamics Research, 43 (5), 055506, DOI: 10.1088/0169-5983/43/5/055506.

Gao, Y. Y., Wang, X. K., Tan, D. S., and Tan, S. K., 2013. Particle image velocimetry technique measurements of the near wake behind a cylinder-pair of unequal diameters. Fluid Dynamics Research, 45, 045504, DOI: 10.1088/0169-5983/45/4/ 045504.

Igarashi, T., 1982. Characteristics of a flow around two circular cylinders of different diameters arranged in tandem, 1st report. Bulletin of the Japan Society of Mechanical Engineers, 201: 349-357.

Igarashi, T., 1984. Characteristics of the flow around two circular cylinders arranged in tandem, 2nd report. Bulletin of the Japan Society of Mechanical Engineers, 233: 2380-2387.

Jester, W., and Kallinderis, Y., 2003. Numerical study of incompressible flow about fixed cylinder pairs. Journal of Fluids and Structures, 17: 557-567.

Kitagawa, T., and Ohta, H., 2008. Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number. Journal of Fluids and Structures, 24: 680-699.

Lin, J. C., Yang, Y., and Rockwell, D., 2002. Flow past two cylinders in tandem: Instantaneous and averaged flow structure. Journal of Fluids and Structures, 16 (8): 1059-1071.

Ljungkrona, L., and Sunden, B., 1993. Flow visualization and surface pressure measurement on two tubes in an inline arrangement. Experimental Thermal and Fluid Science, 6: 15-27.

Ljungkrona, L., Norberg, C., and Sunden, B., 1991. Free-stream turbulence and tube spacing effects on surface effects on surface pressure fluctuations for two tubes in an in-line arrangement. Journal of Fluids and Structures, 5: 701-727.

Meneghini, J. R., Saltara, F., Siqueira, C. L. R., and Ferrarijr, J. A., 2001. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. Journal of Fluids and Structures, 15: 327-350.

Mittal, S., and Raghuvanshi, A., 2001. Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. International Journal for Numerical Methods in Fluids, 35: 421-447.

Mittal, S., Kumar, V., and Reghuvanshi, A., 1997. Unsteady incompressible flows past two cylinders in tandem and staggered arrangement. International Journal for Numerical Methods in Fluids, 25: 1315-1344.

Strykowski, B. J., and Sreenivasan, K. R., 1990. On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. Journal of Fluid Mechanics, 218: 71-107.

Sumner, D., 2010. Two circular cylinders in cross-flow: A review. Journal of Fluids and Structures, 26: 849-899.

Sumner, D., Price, S. J., and Paidoussis, M. P., 1999. Tandem cylinders in impulsively started flow. Journal of Fluids and Structures, 13: 955-965.

Sumner, D., Price, S. J., and Paidoussis, M. P., 2000. Flow pat tern identification for two staggered circulation cylinders in cross-flow. Journal of Fluid Mechanics, 411: 263-303.

Xu, G., and Zhou, Y., 2004. Strouhal numbers in the wake of two inline cylinders. Experiments in Fluids, 37: 248-256.

Zdravkovich, M. M., 1977. Review of flow interference between two circular cylinders in various arrangement. Journal of Fluid Engineering, 99: 618-633.

Zdravkovich, M. M., 1987. The effect of interference between circular cylinders in cross flow. Journal of Fluids and Structures, 1: 239-261.

Zhao, M., Cheng, L., Teng, B., and Dong, G., 2007. Hydrodynamic forces on dual cylinders of different diameters in steady currents. Journal of Fluids and Structures, 23: 59-83.

Zhao, M., Cheng, L., Teng, B., and Liang, D. F., 2005. Numerical simulation of viscous flow past two circular cylinders of different diameters. Applied Ocean Research, 27: 39-55.

Zhou, Y., and Yiu, M. W., 2006. Flow structure, momentum and heat transport in a two-tandem-cylinder wake. Journal of Fluid Mechanics, 548: 17-48.

(Edited by Xie Jun)

(Received April 23, 2013; revised June 8, 2013; accepted January 20, 2014)

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2014

* Corresponding author. Tel: 0086-571-88208891

E-mail: yygao@zju.edu.cn