某直列四缸柴油机曲轴模态分析
2014-04-19董小瑞潘翠丽
刘 波 董小瑞 潘翠丽
(中北大学)
0 引言
曲轴作为发动机的主要旋转零部件,它通过连杆把活塞上下的往复运动转变为旋转运动。然而,因曲轴受力情况复杂,在工作中承受旋转质量的离心力、周期性变化的气体压力和往复惯性力的共同作用,这一方面将使曲轴承受弯曲和扭转载荷,并且如若长期处于这种环境,容易造成曲轴的动应力集中,从而产生疲劳裂纹导致曲轴断裂失效〔1〕,另一方面,周期性变化的气体压力也可能造成发动机的标定转速内发生强烈的共振,动应力急剧增加,从而导致曲轴过早出现扭转疲劳和弯曲疲劳而破坏〔2〕。
针对上述问题,仅静力学计算并不能完全满足设计要求,并且曲轴的动力学性能对于发动机的可靠性以及使用寿命都有着决定性的影响。因此,有必要对曲轴进行动力学分析。而模态分析是动力学分析的基础内容,其结构和系统的振动特性决定了结构和系统对于其他各自动力载荷的响应情况,并且固有频率和固有振型是由结构的几何形状、材料特性以及约束形式决定的,采用不同的约束对分析结果产生很大的影响,边界条件不同,模态参数也不同〔3〕。
因此,为了更符合实际情况,本文基于ANSYS有限元软件对曲轴进行无约束和有约束模态分析并进行对比,从而获得曲轴前10阶固有频率以及振型,为曲轴的优化设计和技术改进提供重要的参考依据。
1 曲轴有限元模型的建立
1.1 曲轴三维模型建立及有限元划分
本文用Pro/E软件建立曲轴三维模型如下图1所示。

图1 曲轴三维模型
由于导入曲面数据时存在缝隙、重叠、错位缺陷,以及软件之间接口技术的问题等,导入后的模型有可能会产生一些无法预知的缺陷,影响网格划分的质量,严重时可能还会导致网格无法划分〔4〕。因此,考虑到ANSA软件有限元网格划分和几何清理的快捷性和方便性,本文先利用ANSA软件对曲轴油孔处、某些无关紧要的微小特征处进行必要的几何清理 (但仍考虑),使之获得较好的网格,然后选用SOLID185单元对其进行四面体网格划分如下图2所示。单元数为1693089个,节点数为328956个

图2 曲轴有限元模型
1.2 曲轴材料的主要特性参数

表1 曲轴材料特性参数
2 模态分析的有限元基础
根据振动理论及其有限元理论,具有有限个自由度弹性系统的振动微分方程为:

式中,[M]、[C]、[K]分别为结构的总质量矩阵、结
构总阻尼矩阵、结构总刚度矩阵;
度向量和位移向量;
{ F (t)}为结构的激振力向量。
将曲轴离散为有限个三维实体单元,分别求出每个单元的刚度矩阵为:

式中,[D]—弹性矩阵;
[Bi]、[Bj]— 应力、应变关系矩阵。
每个单元的质量矩阵为:
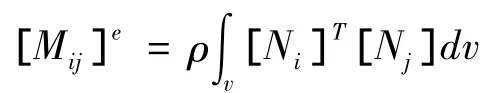
式中,[Ni]、[Nj]— 形函数矩阵;
ρ—单元质量密度。
形成单元的单元刚度矩阵和质量矩阵后,按照单元节点自由度和总体节点自由度的一一对应关系,将其构成结构的总体刚度矩阵[K]和总体质量矩阵[M]。如果节点上有附加质量块,则将它叠加到总体质量矩阵对应的节点自由度位置上,根据边界条件对总体刚度矩阵[K]和总体质量矩阵[M]进行降阶,即可得到给定边界条件下的总体刚度矩阵[K]和总体质量矩阵[M]。在模态分析中,没有激振力的作用,故取 { F (t )} = {0},得到系统自由振动方程。再求解结构自由振动固有频率和振型,因结构阻尼较小,对结构固有频率和振型影响甚微,可忽略不计,由此可以得到结构无阻尼自由振动的运动微分方程:
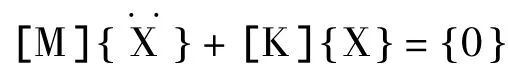
所对应的特征方程是:

式中:ω是系统的固有频率。
系统自由振动特性 (固有频率和振型)的求解问题就是求矩阵特征值和特征向量{}X的问题〔5〕。
3 曲轴的模态分析
有限元模态分析法中分块的兰索斯法 (Block Lanczos)采用稀疏矩阵求解器,精度与子空间迭代法一样好,且省时间,对病态矩阵反应较好,但对内存要求较高,适合大自由度提取多阶模态的情况〔6〕。因此,本文采用ANSYS模态分析中的Block Lanczos法分别对曲轴进行了有约束和无约束模态有限元分析,并且在分析过程中,所需计算精度根据所谓的P方法 (即在不增加单元数目的情况下,通过提高单元形状函数及位移函数的阶次来提高计算精度)来达到〔7〕。
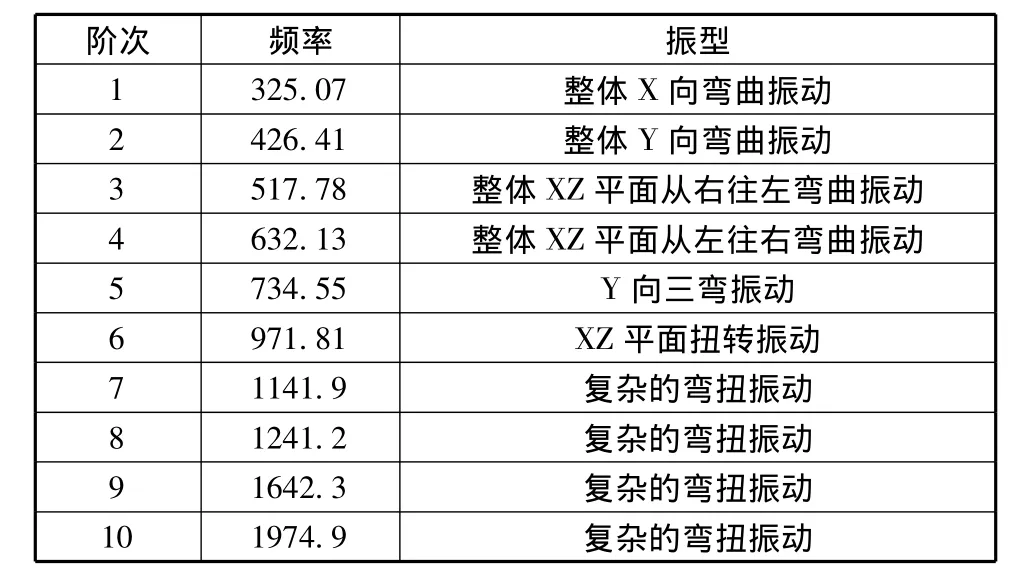
表2 前10阶无约束模态的固有频率和最大变形量
3.1 无约束模态分析
对于自由模态,因具有6阶刚体模态,因此,模态分析求解的曲轴前6阶固有频率为0或者近似为0,第七阶为真正意义上的第一阶固有频率。利用ANSYS软件求得的前10阶无约束模态振型频率和模态振型图见表2和图3~图12所示。

图3 第1阶模态振型

图4 第2阶模态振型

图5 第3阶模态振型

图6 第4阶模态振型

图7 第5阶模态振型

图8 第6阶模态振型

图9 第7阶模态振型

图10 第8阶模态振型

图12 第10阶模态振型
3.2 有约束模态分析
在实际中,曲轴受到主轴承和纵向止推轴承约束,主轴颈与滑动轴承之间存在间隙,依靠两者之间的压力油膜进行润滑。由于载荷作用,主轴颈在上、下轴瓦之间会发生弯曲产生相应的变形,而纵向止推轴承则可以有效地防止曲轴发生轴向窜动,从而保证连杆活塞组正常工作〔8〕。因此本文针对曲轴两端两个主轴颈的表面径向对称约束,同时施加轴向 (X方向)位移约束进行曲轴整体模态分析,求得10阶有约束模态振型频率和模态振型图见表3和图13~图22所示。
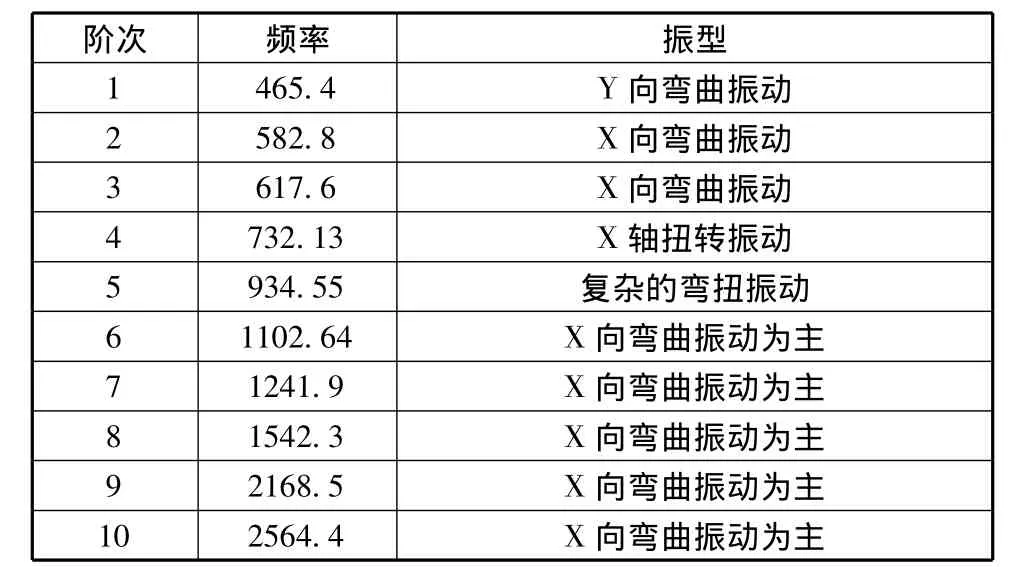
表3 前10阶有约束模态的固有频率和最大变形量

图13 第1阶模态振型

图14 第2阶模态振型

图15 第3阶模态振型

图16 第4阶模态振型

图17 第5阶模态振型

图18 第6阶模态振型

图19 第7阶模态振型
由表2和图3-图12可知,无约束曲轴的模态分析则既包含了简单的弯曲振动或扭转振动,也包含复杂的弯扭振动;由表3和图13-图22可知有约束的曲轴模态分析振型主要是弯曲振动;由图23可知,有约束模态和无约束模态在各模态阶数所对应的频率有所不同,前者比后者频率大,充分说明固有频率和固有振型与约束形式有关。
4 结论
在ANSYS中进行模态分析,可以比较详细地了解系统固有频率,对生产设计时考虑系统的频率有一定的参考意义;
探求了有约束模态分析和无约束模态分析的区别,得出前者在各阶模态的频率比后者大;
有约束的曲轴模态分析振型主要是弯曲振动,而无约束曲轴的模态分析则既包含了简单的弯曲振动或扭转振动,也包含复杂的弯扭振动,从而为曲轴的优化设计和技术改进提供了重要的参考依据。

图20 第8阶模态振型

图21 第9阶模态振型

图22 第10阶模态振型
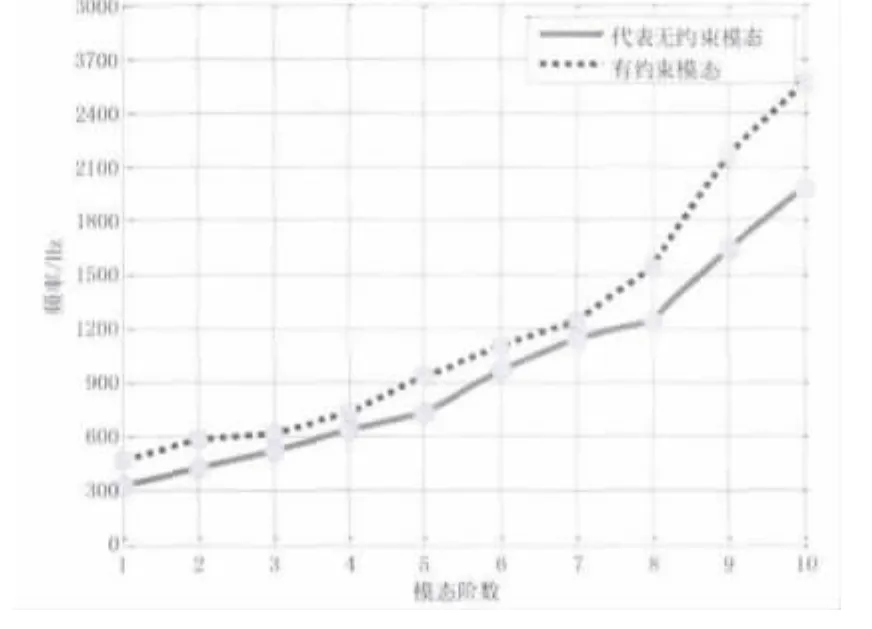
图23 无约束模态和有约束模态频率对比
〔1〕宋晓玲.基于有限元技术曲轴的动力学性能研究〔J〕.制造业自动化,2012,34(2):56-59.
〔2〕孙连科,唐斌,薛冬新,宋希庚.6110柴油机曲轴的三维有限元分析〔J〕.车用发动机,2007(2):81-84.
〔3〕迟志伟,宋希庚,薛冬新等.基于ANSYS的6110柴油机曲轴有限元分析〔J〕.小型内燃机与摩托车,2009,38(3):1-4.
〔4〕史建祥,苏铁熊.柴油机曲轴疲劳寿命预测方法研究〔D〕,山西:中北大学,2013.
〔5〕罗伯特.D.库克,戴维.S.马尔库斯,迈克尔.E.普利沙等.有限元分析的概念与应用〔M〕.西安交通大学出版社,2007.
〔6〕周海超,左言言,鲍林晓.四缸柴油机曲轴的自由模态分析〔J〕.噪声与振动控制,2010(6):63-66.
〔7〕张江林,张建亭.四缸直列柴油机缸体模态分析〔J〕.煤矿机械,2005(8):50-51.
〔8〕蔡进军,吴应军,占泽晟.基于CATIA和ANSYS的六缸曲轴有限元模态分析〔J〕.汽车工程师,2011(1):29-31.
