Predicting Effective Elastic Moduli and Strength of Ternary Blends with Core–Shell Structure by Second–Order Two–Scale Method

Y.T.Wu,J.Z.Cui,Y.F.Nieand Y.Zhang

1 Introduction

Polymer blending has been widely applied to the design of high–performance and functional materials in science and engineering because of its lower cost than synthesizing new polymers[Malik,HallandGenzer(2013);Liebscher,Blais,Potschke and Heinrich(2013);Cohen,Zonder,Ophir,Kenig,McCarthy,Barry and Mead(2013);Yu,Zhou and Zhou(2010);Yin,Zhao,Yang,Pan and Yang(2006)].Apart from the dependence on the properties of component materials,effective properties of polymer blends depend greatly on the microscopic morphology.Common morphology of binary blends are the sea–island morphology,the co–continuous morphology and the salami morphology.For ternary blends,two phases may disperse separately in a continuous matrix phase,or form core–shell particles that disperse in the matrix phase.Due to their high performance,a lot of work has focused on the preparation of ternary blends filled with core–shell structures;examples are HDPE/PS/PMMA[Reignier and Favis(2000)],PA6/PB–g–MA/LDPE[Ke,Shi,Yin,Li and Mai(2008)]and PMMA/PP/PS[Valera,Morita and Demarquette(2006)].In their works,Yin et al.[Yin,Li,Zhou,Gong,Yang and Xie(2013);Zhou,Wang,Dou,Li,Yin and Yang(2013);Dou,Wang,Zhou,Li,Gong,Yin and Yang(2013);Li,Yin,Zhou,Gong,Yang,Xie and Chen(2012)]have prepared PA6/EPDM–g–MA/HDPE ternary blend with core–shell structures(core:HDPE,shell:EPDM–g–MA in PA6 matrix)by controlling some thermodynamic factors and kinetic factors(see Fig.1).The effect of core–shell structure–filled morphology on the rheological behavior,crystallization behavior and mechanical behavior were discussed.The notched impact strength is considerably improved in the ternary blend with core–shell structures.That is,the notched Izod impact strength of the ternary blend is 4–5 times higher than that of PA6/EPDM–g–MA binary blend and 9–10 times higher than that of pure PA6.

Figure 1:SEM photo(a)and TEM photo(b)of PA6/EPDM–g–MA/HDPE(70/15/15 wt%)ternary blend with core–shell structures[Li,Yin,Zhou,Gong,Yang,Xie and Chen(2012)].

Studying the relationship between the mechanical properties and the microscopic morphology of heterogeneous materials is the key to design and optimize high–performance and functional materials.Compared to experiment,numerical simu-lation and theoretical prediction are always economic ways to study the effect of morphology on the effective properties of heterogeneous materials.Homogenization has been widely used to predict the effective properties of heterogeneous materials[Bishay and Atluri(2012);Dong and Atluri(2012);Dong,Gamal and Atluri(2013);Ma,Temizer and Wriggers(2011);Zohdi and Wriggers(2005);Kanit,Forest,Galliet,Mounoury and Jeulin(2003)].Three categories of homogenization methods are commonly used,namely effective medium methods(e.g.,self–consistent method and Mori–Tanaka method),upper and lower bounding methods(e.g.,Voigt–Reuss bounds and Hashin–Shtrikman bounds)and numerical methods(e.g.,finite element method and boundary element method).Macroscopic behavior of heterogeneous materials can be captured effectively by homogenization.On the other hand,multiscale methods have attracted the attention of many researchers.Among them,the two–scale asymptotic homogenization method possesses rigorous mathematical theory,and has been applied to the prediction of effective properties such as thermal properties,elastic properties,elastic–plastic properties and viscoelastic properties for heterogeneous materials[Yu,Cui and Han(2009);Han,Cui and Yu(2010);Yang and Cui(2013);Yi,Park and Youn(1998);Ghosh,Lee and Moorthy(1996)].

The effective thermal conductivity of polymer nanocomposites was predicted by homogenization in[Shin,Yang,Chang,Yu and Cho(2013)].To account for the thermal resistance at the interface and the immobilized interphase,a four–phase equivalent continuum model was introduced.Kaiser et al.[Kaiser and Stommel(2012)]predicted the strength of short fiber reinforced polymers by embedding strength criteria in a homogenization method.The effective elastic–plastic properties of a polymer blend comprising elastic rubber spheres in an elastic–plastic glassy polymer matrix was estimated by a finite element–based homogenization method in[Khdir,Kanit,Zairi and Nait-Abdelaziz(2013)].It was found that the effective properties of the binary blend can be accurately determined by a sufficient number of small microstructures.Song et al.[Song and Youn(2006)]investigated the effective elastic properties of carbon nanotube–filled nanocomposites by thefirst–order two–scale asymptotic homogenization method.The method was validated by comparing the predicted effective elasticity tensor with analytical and experimental results.Considering that the first–order asymptotic homogenization method provides microscopic fields inε–cell area with very low accuracy,Han et al.[Han,Cui and Yu(2008)]developed higher–order asymptotic homogenization method.The second–order two–scale expressions for the microscopic stress and strain fields were developed.The stiffness and strength of several core–shell particle–filled polymer composites were predicted by the method.So far,there are a limited number of studies available in the literature that adopt numerical meth-ods to investigate the effective properties of ternary polymer blends with core–shell structures.

The main task of this paper is to predict effective elastic properties and strength of PA6/EPDM–g–MA/HDPE ternary blend by the second–order two–scale method.To study the relationship between mechanical properties and morphology of the ternary blend,the effect of shell thickness on the effective elastic moduli and tensile yield strength is investigated.In actual microscopic morphology of PA6/EPDM–g–MA/HDPE ternary blend,there are some isolated EPDM–g–MA particles and HDPE particles in PA6 matrix besides EPDM–g–MA/HDPE core–shell structures.Random microstructures in three–dimensional space that closely resemble the actual ternary blend’s morphology are generated by computer.Since the yield strength prediction of heterogeneous materials depends greatly on the yield criterion used,selecting an appropriate yield criterion is very important in the second–order two–scale method.For this purpose,the unified strength theory is introduced.To validate the method,the effective elastic moduli and tensile yield strength predicted are compared with experimental and analytical results.

The remainder of this paper is outlined as follows.A brief introduction of the second–order two–scale method and the limit analysis problem for tensile yield strength is presented in section 2.The geometry modeling and mesh generation of PA6/EPDM–g–MA/HDPE ternary blend are explained in section 3.Numerical results of the effective elastic moduli and strength for the ternary blend are shown in section 4.It includes validation of the method,selection of yield criterion and investigation of the effect of shell thickness on the effective properties of the ternary blend.Some conclusions are drawn in the last section.

2 Description of the numerical method

2.1 Second–order two–scale method

The second–order two–scale method has been developed by Cui et al.in[Han,Cui and Yu(2008);Li(2004)].As shown in Fig.1,PA6/EPDM–g–MA/HDPE ternary blends are random heterogeneous materials at the microscale.Compared to the characteristic length of the macroscopic structure,the characteristic length of the microscopic heterogeneities is sufficiently small,i.e.,Lmicro?Lmacro;see Fig.2.It is assumed that there are two scales in the heterogeneous materials.The microscopic morphology of the heterogeneous materials is assumed to be consistently random.That is,the probability model of the particles in the matrix is the same everywhere in the structure.

Let us consider the elastic problem in the structureoccupied by random heterogeneous materials

Figure 2:Schematic diagram of random heterogeneous materials at the macroscale and microscale.

The displacement¯uand tractionare described on the boundaryandrespectively.nis the outward unit normal vector andfis the body force.The fourth–order stiffness tensoraεchanges rapidly asxvaries at the macroscale.A parameterε?1,which means the ratio of the characteristic length of the oscillation and the characteristic length of the region Ω,is then introduced to describe the multiscale feature.Parameterωdenotes a realization of the random heterogeneous materials.σεis the Cauchy stress tensor,eεis the strain tensor,anduεis the displacement.In the second–order two–scale method,the displacement of the elastic problem(Eq.1)has a formal asymptotic expansion of the form

whereωsis a realization of the random heterogeneous materials in the unit cellQs,andξis the local coordinate.α1,α2=1,...,d.Einstein summation convention on repeated indices is used here.Due to

when substituting Eq.2 into Eq.1 and equating coefficients of the same powers ofε,it is found that,u0is the solution of the homogenized problem

Note thatu0is a macroscopic function which does not obviously depend onξandω.In contrast,Nα1(ξ,ωs)andNα1α2(ξ,ωs)ared–order matrix–valued functions defined inQs,which depend onξandω.These functions satisfy the following boundary value problems respectively

Eq.5 is solved numerically first by finite element method.Afteris obtained,effective stiffness tensorin Eq.6 is computed by the formula

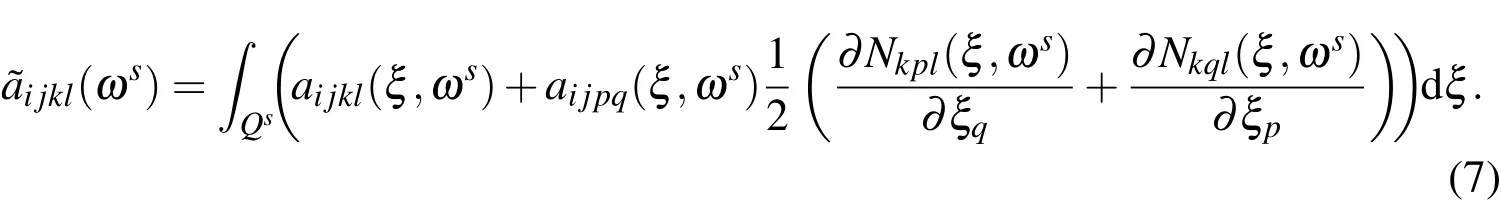
Then we can solve Eq.6 by finite element method to obtainApparentlyin Eq.7 is a random variable dependent on the realizationωs.The deterministic effective stiffness tensorin the homogenized problem(Eq.4)is determined as the mathematical expectation of.Letbe indepen-dent and identically distributed random variables,Kolmogorov’s strong law of large numbers indicates that

is calculated as an approximation of the effective stiffness tensor¯.The accuracy of the approximationdepends on the sample sizeN.

In fact,a¯ depends on the size ofε–cell.Under zero displacement boundary condition,it was found that¯ converges to the true effective stiffness tensor with the first–order accuracy as theε–cell size goes to infinity.Compared to the homogenization and multiscale methods,more accurate effective elastic properties have been obtained by Richardson extrapolation technique with reduced amount of computations[Wu,Nie and Yang(2014)].That is,the extrapolation result

With accurate effective elastic coefficients,Eq.4 is solved to get the homogenized solutionu0(x).Finally,we could compute the second–order two–scale solution from Eq.2.

2.2 Strength prediction

To predict the tensile yield strength for random heterogeneous materials,the following limit analysis problem is considered

Find Σt=max Σ,such that

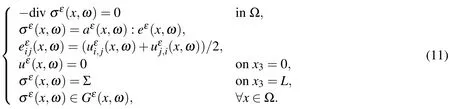
The shape of the structure Ω is a column with rectangular cross section.Assuming the axis of the column is parallel to thex3–axis,the macroscopic traction Σ is loaded on the surface atx3=LwhereLis the length of the column,and the surface atx3=0 is fixed.Gεis the material strength domain at pointxwhich is defined as

whereis the yield function defined by certain yield criteria.The tensile yield strength Σtof the heterogeneous materials is dominated by the tensile yield strength of component materials and is determined by solving this problem.

The second–order two–scale method approximates the multiscale solutionuεof Eq.11 by the second–order two–scale solution.That is,

Find Σt=max Σ,such that

To predict the tensile yield strength Σt,the homogenized problem is solved at the macroscale and it is required that the second–order two–scale stress fieldσε2is not outside the strength domainGε.

Taking into consideration the randomness of the heterogeneous materials,the tensile yield strength is defined as

based on Kolmogorov’s strong law of large numbers.In the equation,Σt,i(i=1,2,...)are independent and identically distributed random variables.

3 Morphology and mesh of the ternary blend

In PA6/EPDM–g–MA/HDPE ternary blend,the core–shell particles are uniformly distributed in the matrix and these particles can be considered as spheres[Dou,Wang,Zhou,Li,Gong,Yin and Yang(2013)].To predict the mechanical properties of the ternary blend by the second–order two–scale method,the microscopic morphology in the unit cell should be generated first.However,it is difficult to use CAD software to generate the morphology of random heterogeneous materials,because the number of particles in the unit cell is large and a lot of random unit cells need to be generated.Furthermore,it is difficult to generate the morphology based on the digital images of actual random heterogeneous materials in three–dimensional space.Yu et al.[Yu,Cui and Han(2008)]proposed an effective computer generation method to construct the morphology of unit cells filled with randomly distributed particles.The morphology of the unit cell is described by the probability distribution which reflects the randomness of particles.Since all of the size,position and orientation of every particle are random variables,and the shape of particles can be sphere,ellipsoid and polyhedron,complex morphology of actual random heterogeneous materials can be simulated by the method.In addition,for the purpose of solving Eq.5 and Eq.6 by the finite element method,a fast mesh generation method was developed by Han et al.[Han,Cui and Yu(2008)]for the randomly distributed ellipsoid–filled unit cell.High–quality mesh can be generated by handling the sliver elements and smoothing the mesh further.The core–shell structures have also been constructed and the mesh has been generated for the shells.

Tetrahedron elements are more adaptable for complex geometry of structures in three–dimensional space.The tetrahedron elements are generated for both matrix and particles in the unit cell comprising some randomly distributed particles.To generate the core–shell structures,the internal surface and external surface of an ellipsoid are assumed to be concentric ellipsoidal surfaces.Firstly,the tetrahedron elements inside an ellipsoid are shrunk around the centroid at the same rate which is calculated by the volume fractions of the shell and core,and then the internal and external surfaces of the shell are obtained.Next the corresponding nodes on the internal and external surfaces are connected to construct triangular prism elements.Finally refined triangular prism elements are generated by partitioning the triangular prisms along their length.

Apart from EPDM–g–MA/HDPE core–shell particles,there are some pure EPDM–g–MA particles and pure HDPE particles in actual PA6/EPDM–g–MA/HDPE ternary blend.When the weight ratio of three component materials is fixed,the ratio of pure particles is correlated to the thickness of shells in the core–shell particles which has great effect on the mechanical properties of the ternary blend.Pure particles were not considered in the polymer composites filled with core–shell structures in[Han,Cui and Yu(2008)].In this paper,more realistic morphology of polymer blends composed of both pure particles and core–shell particles is generated.To this end,we first input some data such as the volume fractions of three component materials,the volume fractions of pure EPDM–g–MA and HDPE particles,and the thickness of shells into the algorithm.Then we generate the morphology of the unit cell filled with particles and partition tetrahedron elements for the matrix and particles.The volume fraction of particles is the sum of the volume fractions of EPDM–g–MA and HDPE.Next the particles are divided into three types,that is,EPDM–g–MA/HDPE core–shell particles,pure EPDM–g–MA particles and pure HDPE particles.Considering that the pure particles are randomly distributed in the unit cell,a particle is selected randomly and marked as pure HDPE particle.The volume fraction of the particle is computed and compared to the given volume fraction of pure HDPE particles.If the volume fraction of the particle does not reach the one we set,the procedure is repeated by selecting another particle randomly from the remainder particles and adding up the volume fraction of pure HDPE particles,until the given volume fraction of pure HDPE particles can be reached.Similar procedure is then implemented to select and mark pure EPDM–g–MA particles.The remainder particles will be the core–shell particles.Based on the given thickness of shells,the tetrahedron elements in the particles are shrunk and triangular prism elements are then generated to construct the shell structures.Fig.3 presents unit cells filled with pure particles,with core–shell particles,and with both pure particles and core–shell particles.In the figure,uniformly distributed spherical particles with the same size are generated,because it is difficult to identify the probability distribution of particle’s size by experiment.We mention that more complex morphology comprising ellipsoids with different sizes and orientations can be obtained by the algorithm.In addition,the thickness of shells can also be determined randomly.

Figure 3:Unit cells with pure particles(a),with core–shell particles(b),and with both pure particles and core–shell particles(c).

4 Numerical results

4.1 Validation of the second–order two–scale method

In computations,there are more than 100 particles in every random unit cell,so that the statistical characteristic of the particles can be well reflected and the unit cell can be used to simulate the random morphology of actual heterogeneous materials.The second–order two–scale method is validated by comparing effective elastic properties predicted with the results of Mori–Tanaka method and Hashin–Shtrikman upper and lower bounds.Since those two methods are widely used for two–phase heterogeneous materials,the effective elastic properties of PA6/EPDM–g–MA binary blend computed by the three methods are compared.

The mechanical properties of component materials for simulations are listed in Tab.1.The data is provided by the State Key Laboratory of Polymer Materials Engineering at Sichuan University.As reported in Tab.2,for PA6/EPDM–g–MA binary blend with two different weight ratios[Li,Yin,Zhou,Gong,Yang,Xie and Chen(2012)],the Young’s modulus computed by the second–order two–scale method is outside the Hashin–Shtrikman bounds,while Mori–Tanaka method predicts the effective Young’s modulus inside the Hashin–Shtrikman bounds.On the contrary,the second–order two–scale method provides effective shear modulus that lies in the Hashin–Shtrikman bounds,while Mori–Tanaka method gives the effective shear modulus outside the Hashin–Shtrikman bounds.When integrating Richardson extrapolation technique into the second–order two–scale method,both effective Young’s modulus and effective shear modulus lie in the Hashin–Shtrikman bounds.In addition,there is a big difference of results between the second–order two–scale method and Mori–Tanaka method,while there is a small difference of results between the second–order two–scale method and Hashin–Shtrikman upper bounds.

Table 1: Mechanical properties of component materials in PA6/EPDM–g–MA/HDPE ternary blend.

In fact,Mori–Tanaka method is more suitable for random heterogeneous materials with simple morphology and small volume fraction of reinforcement material.For random heterogeneous materials with a high contrast of component properties,the Hashin–Shtrikman upper and lower bounds are very broad.In contrast,the second–order two–scale method is more effective to predict effective mechanical properties of random heterogeneous materials.Furthermore,microscopic stress and strain fields can be analyzed by the method to predict the strength of random heterogeneous materials.Of course,biggerε–cells are required to obtain more accurate effective properties by using the method directly.In this case,Richardsonextrapolation can be embedded in the method to efficiently provide more accurate results as well as to reduce the amount of computations.

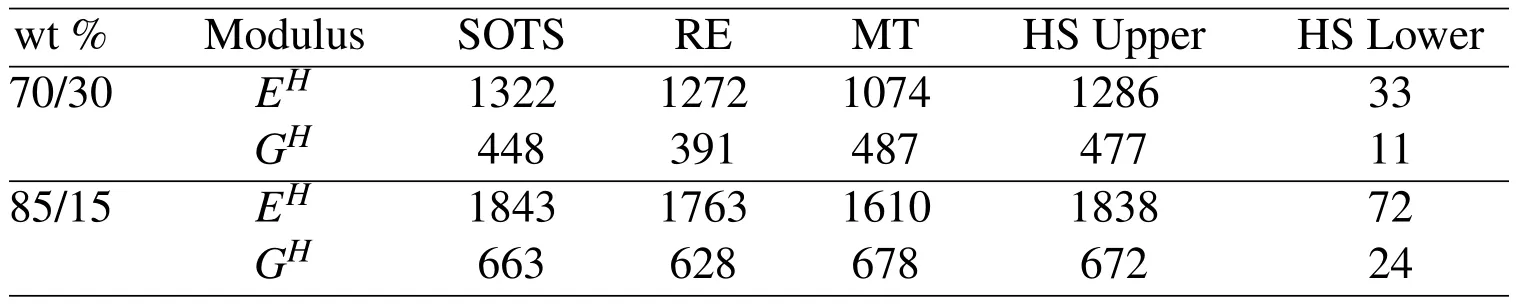
Table 2:Comparison of effective elastic moduli for PA6/EPDM–g–MA binary blend predicted by the second–order two–scale(SOTS)method,Richardson extrapolation(RE),Mori–Tanaka(MT)method and Hashin–Shtrikman(HS)bounds(MPa).

4.2 Effective properties of the ternary blend(70/15/15 wt%)

4.2.1Effect of sample size on the accuracy of simulated results

It is mentioned in section 2 that the sample average is used to estimate the mathematical expectation for both effective stiffness and strength of random heterogeneous materials.The size of sample has an effect on the accuracy of effective stiffness and strength properties.Larger sample size leads to more accurate approximations,but it increases the amount of computations.To choose a suitable sample size,samples with different sizes are used to compute the effective elastic moduli and tensile yield strength of PA6/EPDM–g–MA/HDPE ternary blend.These results are presented in Fig.4.Since the sample average is a random variable,6 samples are generated for every sample size.The mechanical properties of three component materials are listed in Tab.1.

As presented in Fig.4,the simulated effective Young’s modulus lies in the 1%relative error margin of the average(blue solid circles)of these results computed from 6 samples for every sample size,while the simulated tensile yield strength lies in the 1%relative error margin(red dashed line)only when the sample size is as large as 50.In addition,both effective Young’s modulus and tensile yield strength are more dispersive with smaller sample size;see the standard deviation of Young’s modulus as the blue line.On the contrary,increasing sample size leads to centralized data.

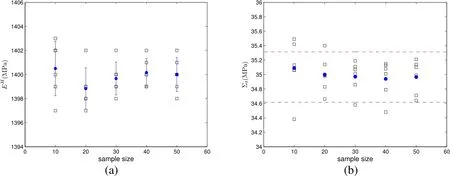
Figure 4:Variation of effective Young’s modulus(a)and tensile yield strength(b)with increasing sample size.

4.2.2Selection of yield criterion

Many strength criteria have been developed in the past century.Several commonly used yield criteria for materials with identical yield strength in tension and compression are the maximum principal stress theory,the maximum principal strain theory,the maximum shear stress theory,the von Mises theory and the twin–shear theory.Each strength theory is suitable for only a certain kind of material.For example,the maximum shear stress theory,the von Mises theory and the twin–shear theory are more suitable for those materials satisfyingτy=0.5σy,τy=0.577σyandτy=0.667σyrespectively,whereτyis the shear yield strength andσyis the tensile yield strength[Yu and Li(2012)].For materials with unequal tensile and compressive yield strength,other strength theories like the Mohr–Coulomb theory and the general twin–shear theory have also been developed.

In[Han,Cui and Yu(2008)],the von Mises theory was adopted to predict strength of composite materials.In order to select a suitable yield criterion in predicting tensile yield strength of PA6/EPDM–g–MA/HDPE ternary blend,effect of different yield criteria on the accuracy of tensile yield strength of the ternary blend is investigated in this paper.For the convenience of testing different yield criteria,the unified strength theory[Yu and Li(2012)]is embedded in the second–order two–scale method.The unified strength theory contains a series of well–known yield criteria,and a lot of new yield criteria can also be derived.

The model of the unified strength theory is expressed as

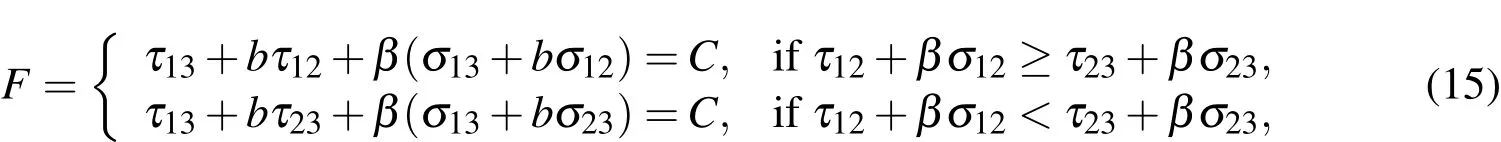
whereτ13,τ12andτ23are three principal shear stresses andτ13is the maximum principal shear stress.σ13,σ12andσ23are the corresponding normal stresses acting on the sections whereτ13,τ12andτ23act.Parameterbcan be used to select different yield criteria.βandCare determined by the formulas

whereσtdenotes the tensile yield strength andσcthe compressive yield strength.When substitutingβandCinto Eq.15,another expression of the unified strength theory reads as

whereσ1,σ2andσ3are the three principal stresses.

Table 3:Typical cases of the unified strength theory.They are the maximum shear stress theory(MSST),approximate von Mises theory(VMT),twin–shear theory(TST),Mohr–Coulomb theory(MCT),general twin–shear theory(GTST),maximum principle stress theory(MPSeT)and maximum principle strain theory(MPSaT).

Table 4:Tensile yield strength Σtof the ternary blend(MPa).

Tab.3 reports some typical yield criteria which can be deduced or approximated by the unified strength theory with different parametersαandb.The unified strength theory is implemented in the second–order two–scale method to investigate the effect of yield criteria on the accuracy of yield strength of random heterogeneous materials.In Tab.4,some simulated tensile yield strengths of PA6/EPDM–g–MA/HDPE ternary blend by different yield criteria are listed.The tensile and compressive yield strength are assumed to be identical for every component material.The tensile yield strength predicted by the second–order two–scale method combined with yield criterion is smaller than the experimental result.And the twin–shear theory predicts the closest result to the experimental one.In the following computations,the twin–shear theory is selected as a suitable strength theory for predicting tensile yield strength of PA6/EPDM–g–MA/HDPE ternary blend.

4.2.3Comparison of simulated and experimental results

The effective elastic moduli and tensile yield strength of PA6/EPDM–g–MA/HDPE ternary blend are presented in Tab.5.The second–order two–scale method predicts effective Young’s modulus and tensile yield strength very close to experimental results.It indicates that the method is effective to predict the mechanical properties of the ternary blend.The simulated effective shear modulus is also listed in Tab.5 for completeness,although it was not measured by experiment.Since the elastic moduli of the constituent materials have a high contrast(see Tab.1),largerε–cells should be generated to get more accurate effective elastic moduli when the second–order two–scale method is used directly.However,this can easily exceed the capability of computers.Richardson extrapolation technique is adopted here to obtain high–precision effective elastic moduli with reduced amount of computer memory and CPU time.

Table 5:Effective elastic moduli and tensile yield strength of the ternary blend.

4.3 Effect of shell thickness on the mechanical properties

4.3.1Varying weight ratio of pure particles

In actual PA6/EPDM–g–MA/HDPE ternary blend,there are three types of particles,namely,EPDM–g–MA/HDPE core–shell particles,pure EPDM–g–MA particles and pure HDPE particles.Since the thickness of shells affects the mechanical properties of the ternary blend,it is valuable to investigate their relationship.With fixed weight ratio of component materials,the thickness of shells can be adjusted by changing the weight ratio of pure particles.For simplicity,it is assumed that only the pure HDPE particles exist in computations,and pure EPDM–g–MA particles are not considered.

Fig.5 presents the variation of shell thickness,effective Young’s modulus,effective shear modulus and tensile yield strength as increasing the weight ratio of pure HDPE particles.The weight ratio is defined as the ratio of pure HDPE particle’s weight to the total HDPE’s weight.The weight ratio of PA6,EPDM–g–MA and HDPE is fixed(70/15/15 wt%).As more HDPE form pure particles,the shell thickness ratio in the core–shell particles is increased.Then both effective elastic moduli and tensile yield strength are increased.When the weight ratio of pure particles is as small as 5 wt%,there is a little effect on the effective elastic moduli and tensile yield strength.

Figure 5:Variation of the shell thickness(a),effective Young’s modulus(b),effective shear modulus(c)and tensile yield strength(d)with different weight ratio of pure HDPE particles.

4.3.2Varying weight ratio of component materials

As shown in the above subsubsection,the shell thickness has a great effect on the mechanical properties of PA6/EPDM–g–MA/HDPE ternary blend.In this subsubsection,we consider the effect of shell thickness further.Only the core–shell particles are generated in the unit cell,and the volume fraction of particles is fixed as 35%.

Figure 6:Variation of the weight ratio of component materials(a),effective Young’s modulus(b),effective shear modulus(c)and tensile yield strength(d)with different shell thickness.

The weight ratios of component materials corresponding to different shell thicknesses are shown in Fig.6.With increasing shell thickness,the effective Young’s modulus,effective shear modulus and tensile yield strength of the ternary blend are also presented in the figure.When increasing the shell thickness,both effective Young’s modulus and effective shear modulus are decreased.It is because the volume fraction of EPDM–g–MA with smaller elastic moduli is increased,while the volume fraction of HDPE with larger elastic moduli is decreased.Meanwhile,the tensile yield strength of the ternary blend is reduced.When the thickness of shells is small,the effective elastic moduli and tensile yield strength decrease apparently as the shell thickness increases.However,the effect of shell thickness is reduced when the shell thickness is large.

5 Conclusions

The second–order two–scale method is used to predict mechanical properties of PA6/EPDM–g–MA/HDPE ternary blend with core–shell structures.Some details in the method’s simulations are discussed.The tensile yield strength predicted with different yield criteria is a little smaller than the experimental result and the twin–shear theory provides the closest result to the experimental one.The method can effectively predict the effective elastic moduli and tensile yield strength of the ternary blend.

The relationship between shell thickness and mechanical properties of the ternary blend is investigated.With fixed weight ratio of component materials,increasing the content of pure HDPE particles leads to the increase of effective elastic moduli and tensile yield strength.However,the effect is little when only a few pure HDPE particles exist.With fixed volume fraction of particles,increasing the thickness of shells leads to the decrease of effective elastic moduli and tensile yield strength.However the effect is reduced when the shell thickness is large.

Acknowledgement:The support of National Basic Research Program of China(973 program 2012CB025904)is gratefully acknowledged.Furthermore,the authors world like to thank Bo Yin for helpful discussions about polymer blends and providing experimental data.

Bishay,P.;Atluri,S.(2012):High–performance 3d hybrid/mixed,and simple 3d voronoi cell finite elements,for macro– µ–mechanical modeling of solids,without using multi–field variational principles.Cmes–Computer Modeling in Engineering&Sciences,vol.84,no.1,pp.41–97.

Cohen,E.;Zonder,L.;Ophir,A.;Kenig,S.;McCarthy,S.;Barry,C.;Mead,J.(2013): Hierarchical structures composed of confined carbon nanotubes in cocontinuous ternary polymer blends.Macromolecules,vol.46,no.5,pp.1851–1859.

Dong,L.;Atluri,S.(2012): T–trefftz voronoi cell finite elements with elastic/rigid inclusions or voids for micromechanical analysis of composite and porous materials.Cmes–Computer Modeling in Engineering&Sciences,vol.83,no.2,pp.183–219.

Dong,L.;Gamal,S.;Atluri,S.(2013): Stochastic macro material properties,through direct stochastic modeling of heterogeneous microstructures with randomness of constituent properties and topologies,by using trefftz computational grains(tcg).Cmc–Computers Materials&Continua,vol.37,no.1,pp.1–21.

Dou,R.;Wang,W.;Zhou,Y.;Li,L.;Gong,L.;Yin,B.;Yang,M.(2013):Effect of core–shell morphology evolution on the rheology,crystallization,and mechanical properties of pa6/epdm–g–ma/hdpe ternary blend.Journal of Applied Polymer Science,vol.129,no.1,pp.253–262.

Ghosh,S.;Lee,K.;Moorthy,S.(1996): Two scale analysis of heterogeneous elastic–plastic materials with asymptotic homogenization and voronoi cell finite element model.Computer Methods in Applied Mechanics and Engineering,vol.132,no.1–2,pp.63–116.

Han,F.;Cui,J.;Yu,Y.(2008):The statistical two–order and two–scale method for predicting the mechanics parameters of core–shell particle–filled polymer composites.Interaction and Multiscale Mechanics,vol.1,no.2,pp.231–250.

Han,F.;Cui,J.;Yu,Y.(2010): The statistical second–order two–scale method for mechanical properties of statistically inhomogeneous materials.International Journal for Numerical Methods in Engineering,vol.84,no.8,pp.972–988.

Kaiser,J.;Stommel,M.(2012):Micromechanical modeling and strength prediction of short fiber reinforced polymers.Journal of Polymer Engineering,vol.32,no.1,pp.43–52.

Kanit,T.;Forest,S.;Galliet,I.;Mounoury,V.;Jeulin,D.(2003): Determination of the size of the representative volume element for random composites:Statistical and numerical approach.International Journal of Solids and Structures,vol.40,no.13–14,pp.3647–3679.

Ke,Z.;Shi,D.;Yin,J.;Li,R.;Mai,Y.(2008): Facile method of preparing supertough polyamide 6 with low rubber content.Macromolecules,vol.41,no.20,pp.7264–7267.

Khdir,Y.;Kanit,T.;Zairi,F.;Nait-Abdelaziz,M.(2013): Computational homogenization of elastic–plastic composites.International Journal of Solids and Structures,vol.50,no.18,pp.2829–2835.

Li,L.;Yin,B.;Zhou,Y.;Gong,L.;Yang,M.;Xie,B.;Chen,C.(2012):Characterization of pa6/epdm–g–ma/hdpe ternary blends:The role of core–shell structure.Polymer,vol.53,no.14,pp.3043–3051.

Li,Y.(2004):Multi–scale algorithm predicting mechanical/heat parameters of the composite materials with random grain distribution of periodicity.PhD thesis,Chinese Academy of Science,2004.

Liebscher,M.;Blais,M.;Potschke,P.;Heinrich,G.(2013): A morphological study on the dispersion and selective localization behavior of graphene nanoplatelets in immiscible polymer blends of pc and san.Polymer,vol.54,no.21,pp.5875–5882.

Ma,J.;Temizer,I.;Wriggers,P.(2011): Random homogenization analysis in linear elasticity based on analytical bounds and estimates.International Journal of Solids and Structures,vol.48,no.2,pp.280–291.

Malik,R.;Hall,C.;Genzer,J.(2013):Effect of protein–like copolymers composition on the phase separation dynamics of a polymer blend:A monte carlo simulation.Macromolecules,vol.46,no.10,pp.4207–4214.

Reignier,J.;Favis,B.(2000): Control of the subinclusion microstructure in hdpe/ps/pmma ternary blends.Macromolecules,vol.33,no.19,pp.6998–7008.

Shao,J.(2010):Mathematical statistics.Springer.

Shin,H.;Yang,S.;Chang,S.;Yu,S.;Cho,M.(2013):Multiscale homogenization modeling for thermal transport properties of polymer nanocomposites with kapitza thermal resistance.Polymer,vol.54,no.5,pp.1543–1554.

Song,Y.;Youn,J.(2006): Modeling of effective elastic properties for polymer based carbon nanotube composites.Polymer,vol.47,no.5,pp.1741–1748.

Valera,T.;Morita,A.;Demarquette,N.(2006): Study of morphologies of pmma/pp/ps ternary blends.Macromolecules,vol.39,no.7,pp.2663–2675.

Wu,Y.;Nie,Y.;Yang,Z.(2014):Prediction of effective properties for random heterogeneous materials with extrapolation.Archive of Applied Mechanics,vol.84,no.2,pp.247–261.

Yang,Z.;Cui,J.(2013):The statistical second–order two–scale analysis for dynamic thermo–mechanical performances of the composite structure with consistent random distribution of particles.Computational Materials Science,vol.69,pp.359–373.

Yi,Y.;Park,S.;Youn,S.(1998): Asymptotic homogenization of viscoelastic composites with periodic microstructures.International Journal of Solids and Structures,vol.35,no.17,pp.2039–2055.

Yin,B.;Li,L.;Zhou,Y.;Gong,L.;Yang,M.;Xie,B.(2013):Largely improved impact toughness of pa6/epdm–g–ma/hdpe ternary blends:The role of core–shell particles formed in melt processing on preventing micro–crack propagation.Polymer,vol.54,no.7,pp.1938–1947.

Yin,B.;Zhao,Y.;Yang,W.;Pan,M.;Yang,M.(2006):Polycarbonate/liquid crystalline polymer blend:Crystallization of polycarbonate.Polymer,vol.47,no.25,pp.8237–8240.

Yu,M.;Li,J.(2012):Computational plasticity:With emphasis on the application of the unified strength theory.Springer.

Yu,W.;Zhou,W.;Zhou,C.(2010): Linear viscoelasticity of polymer blends with co–continuous morphology.Polymer,vol.51,no.9,pp.2091–2098.

Yu,Y.;Cui,J.;Han,F.(2008): An effective computer generation method for the composites with random distribution of large numbers of heterogeneous grains.Composites Science and Technology,vol.68,no.12,pp.2543–2550.

Yu,Y.;Cui,J.;Han,F.(2009):The statistical second–order two–scale analysis method for heat conduction performances of the composite structure with inconsistent random distribution.Computational Materials Science,vol.46,no.1,pp.151–161.

Zhou,Y.;Wang,W.;Dou,R.;Li,L.;Yin,B.;Yang,M.(2013): Effect of epdm–g–mah on the morphology and properties of pa6/epdm/hdpe ternary blends.Polymer Engineering and Science,vol.53,no.9,pp.1845–1855.

Zohdi,T.;Wriggers,P.(2005):An introduction to computational micromechanics.Lecture notes in applied and computational mechanics.Springer–Verlag Berlin Heidelberg.