An Artificial Boundary Method for Burgers’Equation in the Unbounded Domain

Quan Zheng,Lei Fanand Xuezheng Li

1　Introduction

Burgers’equation is an important and basic parabolic PDE in fluid mechanics[Burgers(1948)].It is a model equation of numerous nonlinear problems in aerodynamics,traffic dynamics and so on.It can be used as a simplified form of Navier-Stokes equations in fluid dynamics.Burgers’equation was first given by H.Bateman(1915),then J.M.Burgers introduced the equation to simulate turbulence problems.When an analytic solution is not available,or the analytic one is not suitable to be used,a numerical method is necessary.Since Burgers’equation possesses complexity and universality of applications,its numerical solution is crucial in theory and practice.Burgers’equation can be converted to heat equation by Hopf-Cole transformation.Even for Burgers’equation with homogeneous Dirichlet boundary condition,the topic of the stability and the convergence is still valuable[Kadalbajoo and Awasthi(2006);Liao(2008)].

In fact,many numerical approaches have been applied to solve evolution equations which include Burgers’equation.They are listed as finite difference method, finite element method, finite volume method,collocation method,spectral element method,etc.Recently,a Local Radial Basis Function Meshless Method is applied for solution of the Burgers’equation with different initial and boundary conditions of various complexities[Hosseini and Hashemi(2011)].Moreover,a Meshless Local Petrov-Galerkin Mixed Collocation Method is developed to solve the Cauchy inverse problems of heat transfer[Zhang,He,Dong,Li,Alotaibi and Atluri(2014)],and a Radial Basis Function Collocation Method is constructed for solving ill-posed time domain inverse problems in systems of nonlinear ODEs[Elgohary,Dong,Junkins and Atluri(2014)].Although tremendous efforts have been devoted to solve the so-called direct problems and inverse problems,the finite difference method among them is early and fundamental in applications and can be combined with other methods[Dhawan,Kapoor,Kumar and Rawat(2012)].The combination scheme of the finite difference method with the discretization of artificial integral boundary conditions,as an important algorithm for solving the PDEs on unbounded domain,needs to be elaborately established and theoretically analyzed.

As well-known,several kinds of problems in the areas of heat transfer, fluid dynamics and other applications are on unbounded domains and are solved numerically by using artificial boundary conditions[Feng(1983);Givoli(1992);Yu(2002);Liu and Yu(2008);Yu and Huang(2008);Zheng,Wang and Li(2011)].The arti ficial boundary methods were obtained for various problems of heat equation on unbounded domains and the feasibility and effectiveness of the methods were shown by the numerical examples[Han and Huang(2002A);Han and Huang(2002B)].Moreover,for the heat equation in a semi-unbounded domain[−1,∞)×[0,∞),Sun and Wu(2004) firstly proved that the finite difference scheme with an artificial boundary condition is uniquely solvable,unconditionally stable and convergent with the order 2 in space and the order 3/2 in time under an energy norm.Wu and Zhang(2011)also obtained the high-order artificial boundary conditions for the heat equation in unbounded domains,but only proved that the reduced initialboundary-value problems were stable.

Furthermore,Han,Wu and Xu(2006)started to consider the nonlinear Burgers’equation in the unbounded domain as follows:

In this paper,we consider the problem(1)-(3)withF≡0 and convert it into an initial value problem of heat equation by using Hopf-Cole transformation in the following.Let

where the sufficiently smooth given function φ(x)has compact support supp{φ(x)}⊂[xl,xr].

In section 2, we derive artificial boundary conditions for the problem (4)-(6). In section 3,we construct a finite difference scheme for solving the problem on bounded computational domain with the artificial boundary conditions.Then a new solution of Burgers’equation is obtained and the difficulty for solving the nonlinear problem is avoided.In section 4,we prove that the finite difference scheme is uniquely solvable,unconditionally stable and convergent with the order 2 in space and 3/2 in time.In section 5,a numerical example con firms the stability and convergence of the finite difference method.

2　The problem with artificial boundary conditions

Let us consider firstly the restriction ofufor the problem(4)-(6)on[xr,+∞)×[0,T] as follows:

We can get the solutionu(x,t)by givenu(xr,t):

Returning to the variable λ we getand taking the limitx→+xrwe obtain a relation betweenut(xr,t)andux(xr,t):ux(xr,t)=

Similarly,we can obtain the artificial boundary condition onx=xl.

So,we reduce the problem(4)-(6)to a problem in the bounded computational domain:

3　The derivation of the difference scheme

In order to derive the finite difference method,the bounded computational domain is divided into anM×Nuniform mesh.Leth=(xr−xl)/M,xi=xl+ihfor 0≤i≤M,τ=T/N,tn=nτ for 0≤n≤N,be the numerical solution ofu(x,t)at(xi,tn).Introduce the notations:

Lemma 1(see[Han and Wu(2012)])Suppose f(t)∈C2[0,tn],then

By introducing a new variablev=∂∂uxto reduce the order of heat equation,the problem(7)-(10)is equivalent to the problem of first-order differential equations:

De fine the grid functions:

Using Lemma 1,it follows from(15)that

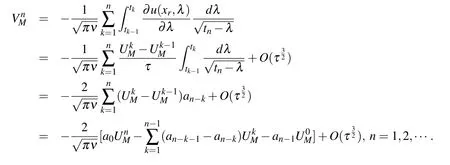
Therefore,we have

and similarly,

Using Taylor expansion,we have

where

andcis a constant.

Thus,we construct a difference scheme for(11)-(15)in the following:

Theorem 1The difference scheme(16)-(20)is equivalent to the following(21)-(25):

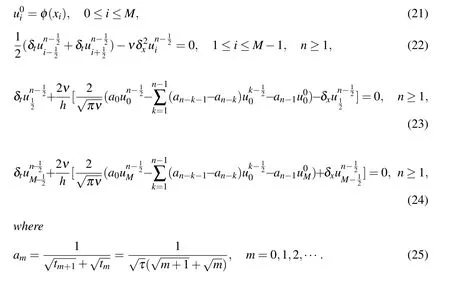
ProofMultiplying(16)byand using(17)we obtain

From(26)and(27)forifrom 1 toM−1 we obtain

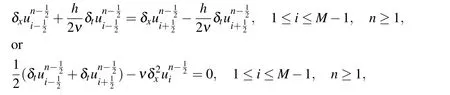
which is(22).

Wheni=0,from(19)and(27),we know that

Dividing byh/2 on the both sides we obtain(23).

Similarly,wheni=M,from(20)and(26),we know that

Dividing byh/2 on the both sides we obtain(24).

The difference scheme(21)-(24)can be sorted as the following:

4　Analysis of the difference scheme

Lemma 2For any F={F1,F2,F3,···},we have

where amis defined in(25).

Proof

Lemma 3Suppose{uni}be the solution of

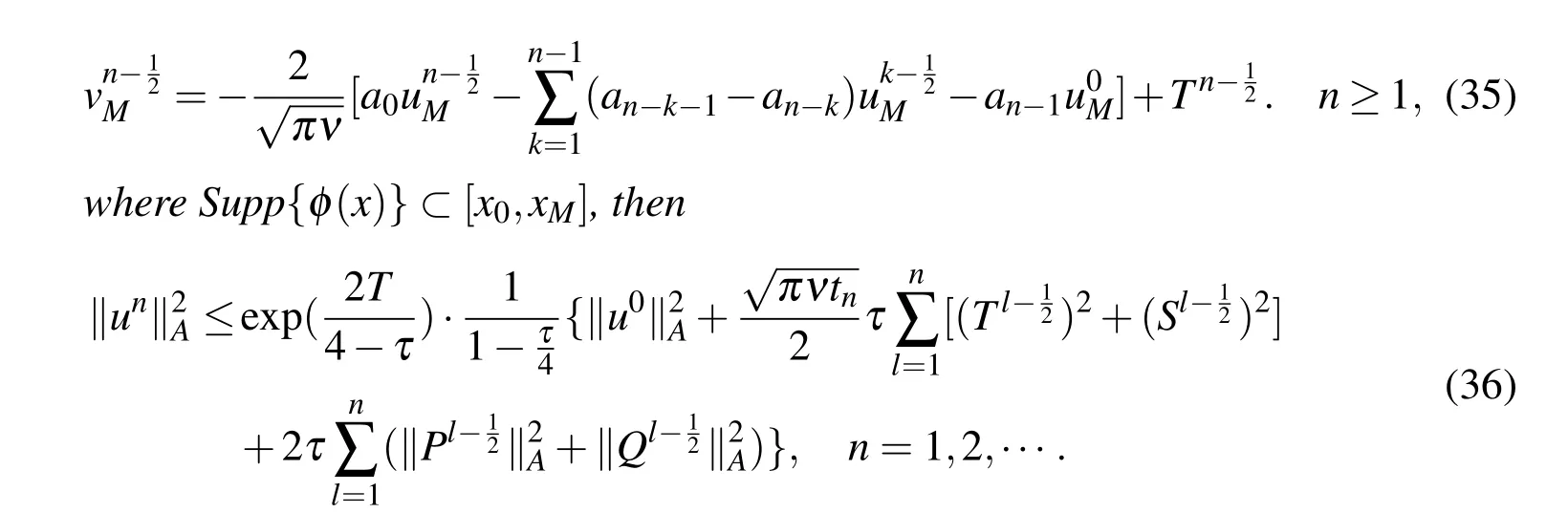
ProofMultiplying(31)byand multiplying(32)by,then adding the results,we have

Multiplying the above inequality by τhand summing up forifrom 1 toM,we obtain

Summing up forlfrom 1 ton,we have

Substituting(34)and(35)into the above inequality,and using Lemma 2,we have

Using Gronwall’s lemma,

Theorem 2The difference scheme(21)-(25)is uniquely solvable.

ProofFrom Theorem 1,it suffices to prove that the difference scheme(16)-(20)is uniquely solvable.When initial value is homogeneous,using Lemma 3,we have kunk2A=0,n=1,2,···.

Theorem 3Let{uni|0≤i≤M,n≥1}be the solution of(21)-(25),then

ProofFrom Theorem 2.2,it suf fices to prove that(39)holds for the difference scheme(16)-(20).Therefore,(39)follows directly from Lemma 3.2.

Theorem 4Suppose that the problem(4)-(6)has solution u(x,t)∈C4,3x,t(R×[0,T]).Let{uni}be the solution of(21)-(25),and let˜uni=Uni−uni,then

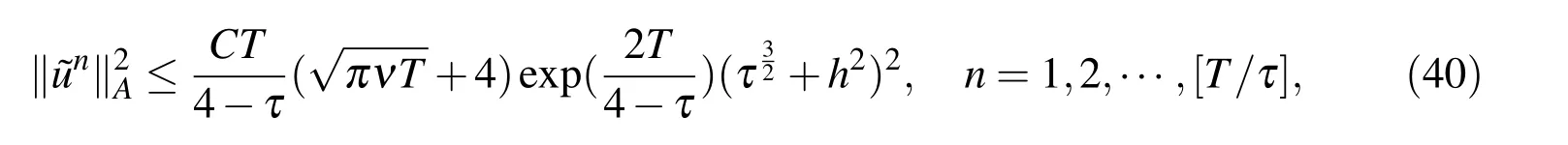
where C is a constant independent ofτand h.

ProofWe obtain the error equations:

Theorem 4 shows that the convergence order of(21)-(24)is 2 in space and 3/2 in time for the problem(7)-(10)of the heat equation with artificial boundary conditions.Finally,the numerical solution of Burgers’equation is obtained by using central difference w.r.t.xas the following:

which keeps the corresponding unique solvability,unconditional stability and convergence in space and in time.

By the way,the arti ficial integral boundary method in[Sun and Wu(2009)]is suitable for the inhomogenous Burgers’equation.For the homogenous problem(4)-(6),it gives

which deduces a discrete boundary condition different from(23),and finally the numerical solution of Burgers’equation is derived from

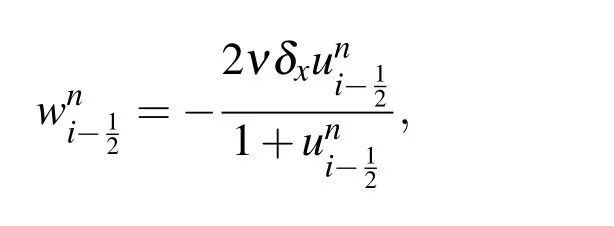
which is slightly different from(41).

5　Numerical examples

We test the stability and accuracy of the proposed method by solving Burgers’equation with an initial conditionThe support offis approximately compact since|f(x)|is small enough outside the computational domain[xl,xr]=[−5,5].The exact solution is

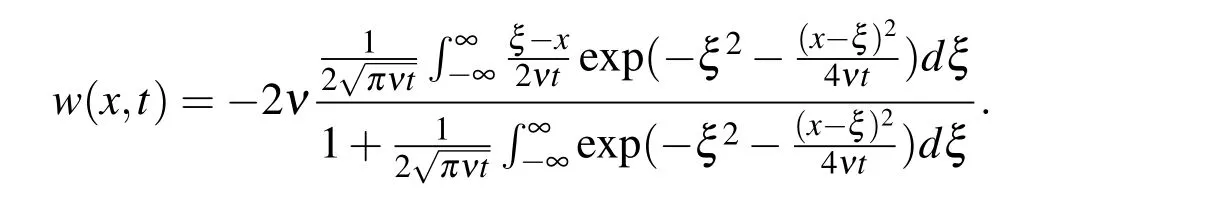
The error of numerical solutions and the convergence order w.r.t τ are shown in table 1.The error of numerical solutions and the convergence order w.r.thare shown in table 2.

10 5000 3.4349e-04—5.0342e-04—　56 3.6538e-03—5.3702e-03—20 5000 8.6462e-05 1.9901 1.2597e-04 1.9987 95 1.2531e-03 1.5439 1.8421e-03 1.5436 40 5000 3.6936e-05 1.2270 3.2692e-05 1.9461 159 4.4110e-04 1.5063 6.4865e-04 1.5058 80 5000 3.1874e-05 0.2126 1.2036e-05 1.4416 267 1.5473e-04 1.5114 2.2819e-04 1.5072 N M L∞-error order L2-error order M L∞-error order L2-error order Table 1:Convergence w.r.t.τ of examples for ν=0.5,T=1,h=0.002 and h=τ3/4.

25 200 1.5826e-02—2.3957e-02—　3 1.7558e-02—2.8237e-02—50 200 4.1785e-03 1.9212 6.2111e-03 1.9475 9 4.5211e-03 1.9574 6.7089e-03 2.0734 100 200 1.0618e-03 1.9765 1.5793e-03 1.9756 22 1.1260e-03 2.0055 1.6559e-03 2.0185 200 200 2.6775e-04 1.9876 3.9703e-04 1.9920 54 2.7728e-04 2.0218 4.0895e-04 2.0176 M N L∞-error order L2-error order N L∞-error order L2-error order Table 2:Convergence w.r.t.h of examples for ν=0.5,T=1,τ=0.005 and τ=h4/3.

6　Concluding Remarks

In this study,motivated by works of Han,Wu,Sun and their co-authors,an artificial boundary method for Burgers’equation in the unbounded domain is presented by(21),(28)-(30)and(41)succinctly.The inequality in Lemma 2 is slightly stronger than that in[Wu and Sun(2004)]and[Han and Wu(2012)].Lemma 3 is proved by using Gron wall’s lemma,a similar Lemma 4 in[Wu and Sun(2004)]for heat equation on the semi-in finite domain,i.e.Lemma 3.2.4 in[Han and Wu(2012)],was incorrectly proved by not using Gronwall’s lemma,and could be modified and proved by the way of Lemma 3.Finally,the suggested method is clearly proved and verified to be uniquely solvable,unconditionally stable and convergent with the order 2 in space and the order 3/2 in time under an energy norm to solve Burgers’equation in the unbounded domain.

Acknowledgement:The research is supported in part by Natural Science Foundation of Beijing(No.1122014)and in part by National Natural Science Foundation of China(11471019).

The authors thank the anonymous reviewers for the valuable comments and suggestions to the paper.

Bateman,H.(1915):Some recent researches in motion of fluids.Mon.Weather Rev.,vol.43,no.4,pp.163-170.

Burgers,J.M.(1948):A mathematical model illustrating the theory of turbulence.Adv.Appl.Mech.,vol.1,no.2,pp.171-199.

Dhawan,S.;Kapoor,S.;Kumar,S.;Rawat,S.(2012):Contemporary review of techniques for the solution of nonlinear Burgers equation.J.Comput.Sci.,vol.3,no.5,pp.405-419.

Elgohary,T.A.;Dong,L.;Junkins,J.L.;Atluri,S.N.(2014):Time Domain Inverse Problems in Nonlinear Systems Using Collocation&Radial Basis Functions.CMES:Comput.Model.Eng.Sci.,vol.100,no.1,pp.59-84.

Enquist,B.;Majda,A.(1977):Absorbing boundary conditions for numerical simulation of waves.Math.Comput.,vol.31,no.139,pp.629-651.

Feng,K.(1983):Finite element method and natural boundary reduction.Proc.of Inter.Cong.Math.,Warszawa,pp.1439-1453.

Givoli,D.(1992):Numerical Methods for Problem in In finite Domains.Amsterdam:Elsevier.

Han,H.-D.;Huang,Z.-Y.(2002A):A class of arti ficial boundary conditions for heat equation in unbounded domains.Comput.Math.Appl.,vol.43,no.6-7,pp.889-900.

Han,H.-D.;Huang,Z.-Y.(2002B):Exact and approximating boundary conditions for the parabolic problems on unbounded domains.Comput.Math.Appl.,vol.44,no.5-6,pp.655-666.

Han,H.-D.;Wu,X.-N.(2012):Artificial Boundary Method.Beijing:Tsinghua University Press/Springer Press.

Han,H.-D.;Wu,X.-N.;Xu,Z.-L.(2006):Artificial boundary method for Burgers’equation using nonlinear boundary conditions.J.Comput.Math.,vol.24,no.3,pp.295-304.

Hosseini,B.;Hashemi,R.(2011):Solution of Burgers equation using a Local-RBF Meshless Method.Inter.J.Comput.Meth.Eng.Sci.&Mech.,Vol.12,no.1,pp.44-58.

Kadalbajoo,M.K.;Awasthi,A.(2006):A numerical method based on Crank-Nicolson scheme for Burgers’equation.Appl.Math.Comput.,vol.182,no.2,pp.1430-1442.

Liao,W.-Y.(2008):An implicit fourth-order compact finite difference scheme for one-dimensional Burgers’equation.Appl.Math.Comput.,vol.206,no.2,pp.755-764.

Liu,D.-J.;Yu,D.-H.(2008):The coupling method of natural boundary element and mixed finite element for stationary Navier-Stokes.CMES:Comput.Model.Eng.Sci.,vol.37,no.3,pp.305-329.

Sun,Z.-Z.;Wu,X.-N.(2009):A difference scheme for Burgers equation in an unbounded domain.Appl.Math.Comput.,vol.209,no.2,pp.285-304.

Wu,X.-N.;Sun,Z.-Z.(2004):Convergence of differences cheme for heat equation in unbounded domains using artificial boundary conditions.Appl.Numer.Math.,vol.50,no.2,pp.261-277.

Wu,X.-N.;Zhang,J.-W.(2011):High-order local absorbing boundary conditions for heat equation in unbounded domains.J.Comput.Math.,vol.29,no.1,pp.74-90.

Yu,D.-H.(2002):Natural Boundary Integral Method and Its Applications.Beijing/Dordrecht/New York/London:Kluwer Academic Publisher/Science Press.

Yu,D.-H.;Huang,H.-Y.(2008):The artificial boundary method for a nonlinear interface problem on unbounded domain.CMES:Comput.Model.Eng.Sci.,vol.35,no.3,pp.227-252.

Zhang,T.;He,Y.;Dong,L.;Li,S.;Alotaibi,A.;Atluri,S.N.(2014):Meshless Local Petrov-Galerkin Mixed Collocation Method for solving Cauchy inverse problems of steady-state heat transfer.CMES:Comput.Model.Eng.Sci.,vol.97,no.6,pp.509-533.

Zheng,Q.;Wang,J.;Li,J.-Y.(2011):The coupling method with the natural boundary reduction on an ellipse for exterior anisotropic problems.CMES:Comput.Model.Eng.Sci.,vol.72,no.2,pp.103-113.