Computational Methods in Engineering:A Variety of Primal&Mixed Methods,with Global&Local Interpolations,for Well-Posed or Ill-Posed BCs

1　Introduction

Most problems in engineering&applied mathematics are characterized by ordinary or partial differential equations.The development of various computational methods for the solution of these ODEs&PDEs has attracted the attention of engineers,physicists and mathematicians for several decades.Being derived from the symmetric Galerkin weak-form with primitive variables such as displacements or temperature,the primal finite element method(FEM)has emerged as one of the most popular methods of computational mechanics,heat transfer,etc.,see[Zienkiew icz and Morice(1971);Atluri(2005)].This may be due to its simplicity and established convergence of the energy norm.However,disadvantages of primal FEM are also well-known,such as difficulty to satisfy higher-order continuity requirements(especially in plates and shells),locking phenomena in problems which involve constraints,inefficiency in solving problems with stress singularities&in finite boundaries,difficulty in solving large deformation problems which involve severe mesh-distortion,and difficulty in solving ill-posed inverse problems,etc.,see[Dong and Atluri(2011)].For example,it is difficult to use the primal formulation of thin-plates(4thorder PDE)to develop primal FEM,which requiresC1continuous element-based trial functions.It is easier to develop FEM,based on the mixed schemes which treat rotations as independent variables,and reduce the continuity requirement by one order[Lee and Pian(1978);Cai,Paik,and Atluri(2010)].When dealing with fluids, finite element methods often result in the notorious"checker-board pattern"for the computed pressures.The Finite volume methods with element-based or meshless trial functions are much more advantageous in computational fluid dynamics as compared to primal or mixed finite elements[Spalding(1972);Patankar(1980);Avila,Han,and Atluri(2011)].For problems which involve stress singularity such as fracture mechanics, and for problems which involve in finite boundaries such as acoustics and electro-magnetics,it is natural to use boundary element methods instead of primal or mixed FEM[Han and Atluri(2002),Dong and Atluri(2013a),Dong and Atluri(2013b),Qian,Han,and Atluri(2013)].For problems which involve large deformation,impact,and penetration,Meshless Local Petrov Galerkin Method(MLPG)has demonstrated significant advantages as compared to mesh-based FEM[Han,Rajendran,and Atluri(2005);Han,Liu,Rajendran,and Atluri(2006)].For ill-posed inverse problems,because FEM cannot accommodate lower-order and higher-order BCs at the same part of the boundary,iterative guessing and optimization has to be resorted to when using FEM to solve ill-posed problems with Cauchy type of BCs.It is more natural to use the collocation method,based on a mixed meshless interpolation to enforce the governing differential equations,as well as lower&higher-order BCs[Zhang,Dong,Alotaibi,and Atluri(2013);Zhang,He,Dong,Li,Alotaibi,and Atluri(2014)].

Each of the above-mentioned computational methods has its own advantages and disadvantages,for the solution of various well-posed and ill-posed engineering problems.However,these methods are all essentially branches of the same tree.As shown in Fig.1.0.1,these computational methods are all based on the idea of weighted residuals,but with different primal or mixed formulations,with different global or local,symmetric or unsymmetric weak forms,different global or local trial functions,as well as different global or local test functions.

Figure 1.0.1:Various computational methods:many branches of the same tree

In this paper,which is primarily of an expository nature,we illustrate various methods for the solution of the 4thorder ODE(y′′′′+y-f=0).In section 2,by directly using the weighted residual integral for the 4thorder ODE,withyas the primitive variable,primal collocation and finite volume method(FVM)are firstly developed and demonstrated,by using the Dirac Delta or the Heaviside function as test functions.Because a 4thorder differentiation of the trial function is involved,C3continuous trial functions are necessary for primal collocation and FVM.C3continuous global trial functions are easy to implement for this 1D problem,but an unsymmetric,fully-populated,ill-conditioned coefficient matrix is to be solved.C3continuous element-based trial functions are too complex to be useful(especially in higher-dimensions).Moreover,it is easy to constructC3continuous local meshless trial functions(such as Moving Least Squares),which leads to the primal MLPG collocation and FVM.However,because of the complexity and the inaccuracy of higher-order derivatives of MLS interpolations,the solutions of MLPG primal collocation and FVM are not satisfactory.Integrations by parts of the weighted residual lead to the primal symmetric weak-form,which reduces the required order of continuity for trial functions,by increasing the requirements on test functions.The global symmetric weak-form leads to the Finite Element Method,with element based interpolation as trial functions.The local symmetric weak-form leads to the MLPG method,with weight functions of MLS as test functions.It is also pointed out that FEM is not suitable for solving ill-posed problems,in that the global symmetric weak-form does not accommodate both lower-order and higher-order BCs to be specified at the same part of boundary.Further integrations by parts of the weighted-residual lead to the unsymmetric weak-form,which can be used to develop global and local boundary integral equations.Global boundary integral equations lead to various types of boundary elements.And local integral equations can be used to develop the MLPG LBIE method.In section 3,the first kind of mixed method is considered,by considering both displacementyand its second derivativey′′as independent variables.On the other hand,if the trial functions are constructed in a way so that they satisfy the governing differential equations a-priori(using Trefftz basis functions or fudamental solutions),directly collocation of the BCs lead to the Trefftz method and the Method of Fundamental Solutions.Similarly,in section 4,the second kind of mixed method is demonstrated,by consideringy，y′，y′′，y′′′as independent variables.The mixed schemes do not involve higher-order differentiations of each variable,so that the required order of continuity for trial functions is reduced,and the algorithmic formulations are simplified.One can use very simple,C0/C1element-based or meshless trial functions,and use Dirac Delta or Heaviside Functions as test functions,to develop simple schemes of mixed element-based/MLPG,collocation or finite volume method,in which the solutions of the primitive variable as well as the mixed variables are obtained simultaneously.M ixed collocation and finite volume methods can also be used to solve Cauchy type of inverse problems without using iterative optimization.This is advantageous because both well-posed and ill-posed BCs can be treated equivalently using the same computational method.In section 5,we complete this study by making some discussions on the advantages&disadvantages of various primal&mixed formulations,global&local,symmetric&unsymmetric weak forms,and global&local interpolations,as well as making some comments on extending all the current computational methods to solve two-&three-dimensional partial differential equations.

2　Problem definition and various primal methods

2.1　The governing ODE with well&ill-posed BCs

After non-dimensionalization,the problem of a beam on elastic foundation can be described by the following 4thorder ODE,as shown in[Atluri(2005)]:

in whichyis the normalized vertical displacement(deflection),andfis the normalized distributed load,and Ω={x|0＜x＜1}is the domain of interest.The boundary conditions are:

whereS,S′,S′′,andS′′′denote the boundary points wherey(displacement),y′(rotation),y′′(moment),andy′′′(shear)are prescribed,respectively.

For the well-posed problem,the prescriptions ofandare mutually disjoint,i.e.

with∂Ω being the boundary pointsx=0，1.Well-posed problems are physically consistent with the solid-body(beam),because when the deflectionyis prescribed,y′′′becomes the shear force reaction to be solved for,and when the rotationy′is prescribed,y′′becomes the moment reaction to be solved for.

Otherwise,if Eq.(2.1.6)does not hold,an ill-posed problemis to be considered.For example,can be all prescribed atx=0,as one may be measuring displacement,rotation,shear and moment all at part of the boundary,and the problem then is to determine the deformation in the other part of the boundary as well as in the whole domain.Ill-posed problems have important engineering applications such as in structural health monitoring,system control,and medical imaging.

In this study,the following well-posed problemis considered for demonstration:

with the analytical solution:

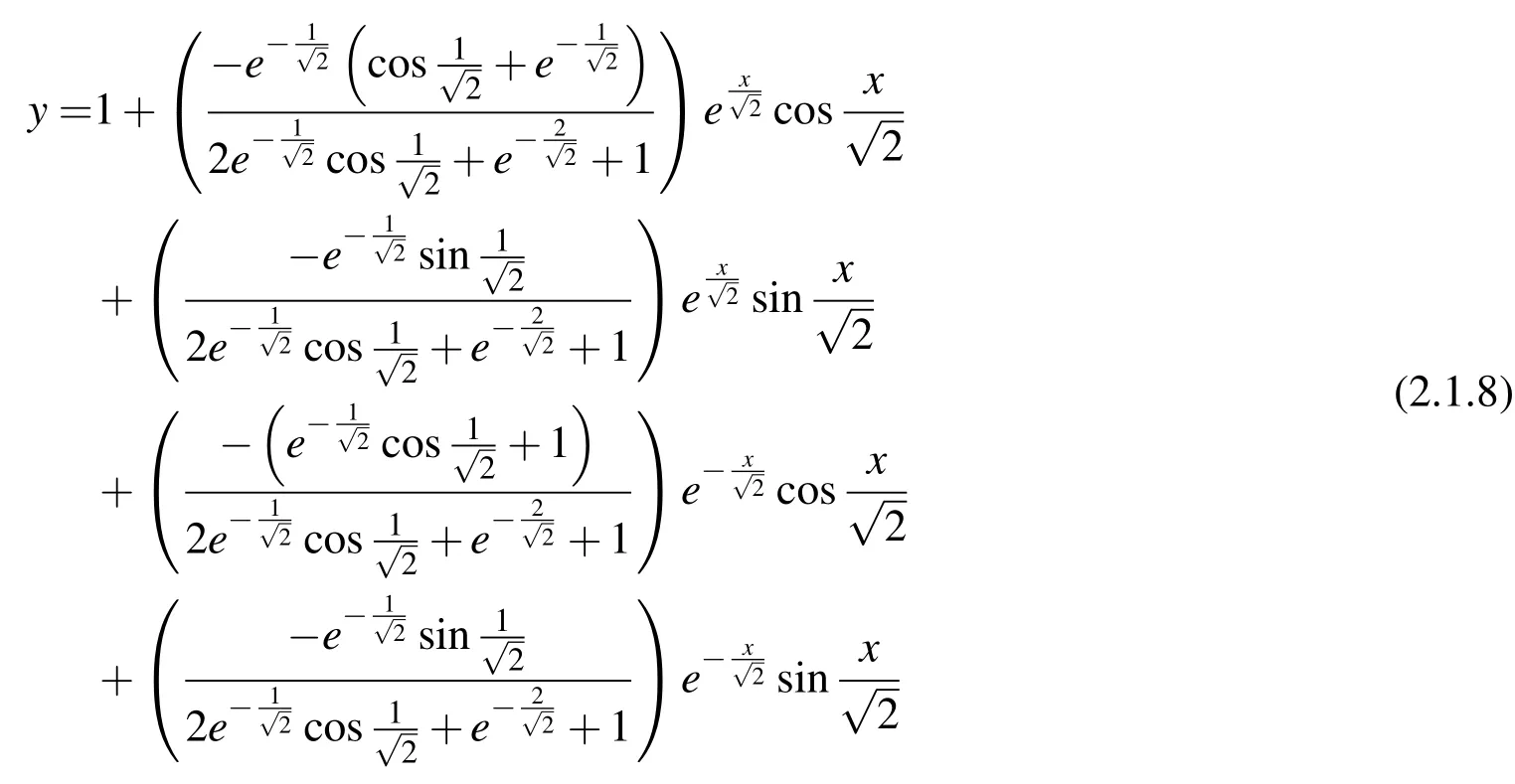
And for illustration,the following ill-posed problemis considered:

with the analytical solution:

2.2　Global weighted-redisudal unsymmetric weak-form-1,globaltrial functions,primal collocation& finite volume methods

2.2.1Global unsymmetric weak-form-1

Considering a trial functionu,the residual error in the differential equation(2.1.1)is:

With a test functionv,the global weighted residual weak-form of the primal formulation can be be written as:

The primal weak form Eq.(2.2.2)involves the fourth-order derivative of the trial function,whereas no differentiation of the test function is involved.Therefore,in order to ensure RΩ(u′′′′+u-f)dxhas a finite value,it is required that the trial functionushould has continuous third order derivative,i.e.ushould beC3functions.VariousC3continuous global trial functions are considered:such as harmonics,polynomials and global RBFs.While local element-basedC3trial functions are too complex to be useful,local meshless interpolations ofu,such as moving least squares,can easily achieve higher-order continuity.On the other hand,the test functionvis not necessarily to be continuous.Dirac Delta function and Heaviside function can be used as test functions,leading to primal collocation and finite volume methods.Detailed discussions of the variety of selected trial and test functions,as well as the computational results for each case are given as follows.

2.2.2Global trial functions,primal collocation method

It is simple to satisfy theC3continuity of trial functions by using global trial functions.In this study,the following global trial functions are explored:

Harmonics:

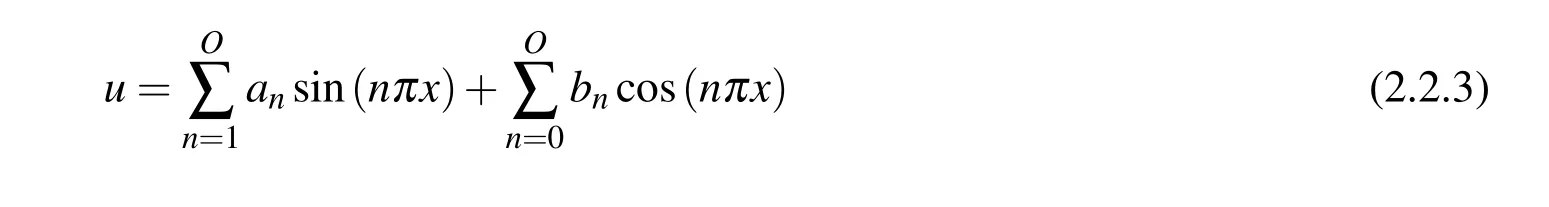
Polynomial:

Radial Basis Function(Gaussian):

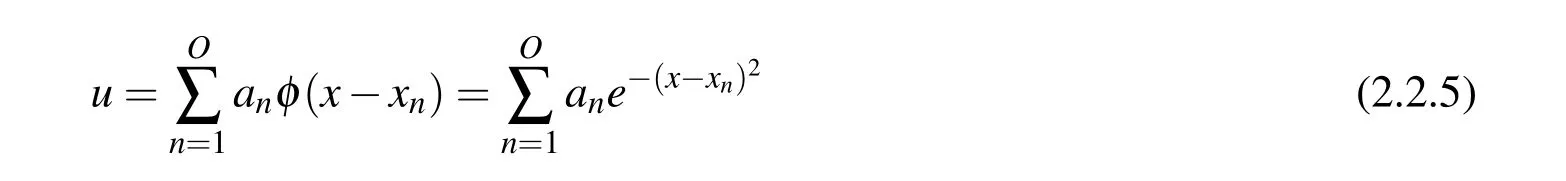
It should be noted that,there are many types of global RBFs that satisfy the requirement ofC3continuity.Discussion of the advantages and disadvantages of each type of RBF is beyond the scope of this study.One may refer to[Chen,Fu,and Chen(2013)]for a comprehensive review of various Radial Basis Functions.Gaussian function is used at here for demonstration.

No matter which kind of global interpolation is used,we can always write the trial function as:

where the columns of Φ represent each of the independent basis functions,and the vectorαcontains undetermined coefficients.

With trial functions being de fined,the simplest method is to use a Dirac Delta function as the test function,i.e.for a group of pre-selected points along the beam:xI，I=1，2，...，N.Substituting the trial and test functions into Eq.(2.2.2),this lead to the enforcement of the 4thoder ODE at each point(the so-called point collocation method):

Similarly,the boundary conditions can be enforced also by collocation:

If the number of equations obtained by Eqs.(2.2.7)and(2.2.8)is equal to or larger than the number undetermined coefficients,then the vector of coefficientsαcan be determined by the method of least squares.It should be noted that,if the global RBFs are used as the trial function of the solution,the collocation points can be either the same as or different from RBF center(source)points.

Firstly we use the primal collocation method with global interpolations to solve this well-posed problem given in Eq.(2.1.7).The analytical solutions ofy(displacement),y′(rotation),y′′(moment)are given in Fig.2.2.1.Harmonics,polynomials and global RBFs are used as trial functions.For each case,O=15 in Eqs.(2.2.3)-(2.2.5)are used.The same number of collocation points are used as the number of undetermined coefficients,which are uniformly distributed along the beam,for the collocation of the 4thorder ODE.Additional 4 equations are obtained by collocation of the boundary conditions.The computational errors are given in Figs.(2.2.2)-(2.2.4),with the following definition of errors:

In a similar fashion,we use the primal collocation method with global interpolations to solve this ill-posed problem given in Eq.(2.1.9).The analytical solutions ofy(displacement),y′(rotation),y′′(moment)are given in Fig.2.2.6.The same global trial functions and collocation pointed are adopted.The computational errors are given in Figs.2.2.5-2.2.8.

It can be seen that the current simple scheme of primal collocation method can deal with both well-posed and ill-posed BCs quite easily.However,there are several disadvantages of the global trial functions such as Harmonics,Polynomials,and RBFs.

Incompleteness:For this simple one-dimensional problem,it is easy to conclude that all the admissible trial solutions can be expressed in terms of Fourier series,Power series,or global RBFs.However,for high-dimensional problems,which involve multiply-connected domains or even cracks,it is obviously incomplete to use Fourier series or Power series as trial solutions.This will lead to large computational errors of the numerical solutions.On the other hand,global RBFs,and element-based local interpolations,as well as meshless local interpolations such as Moving Least Squares and local RBFs,are more complete compared to Harmonics and Polynomials.

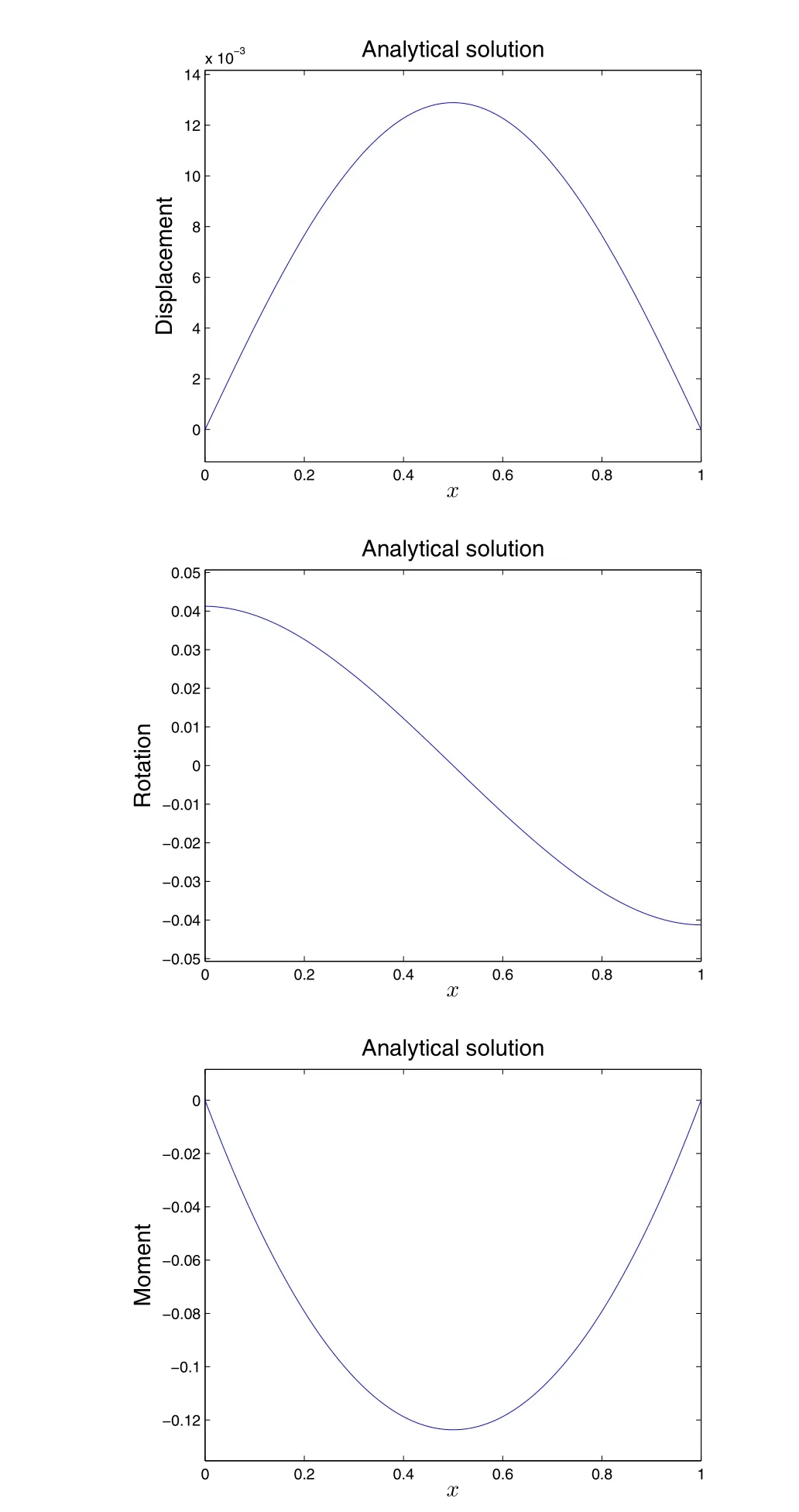
Figure 2.2.1:Analytical solution of the well-posed problem given in Eq.(2.1.7)

Figure 2.2.2:Solution of the well-posed problem given in Eq.(2.1.7),by the primal collocation method,with Harmonics as trial functions.O=15 is used in Eq.(2.2.3).31 points are uniformly distributed within 0≤x≤1 for the collocation of the 4th order ODE.

Figure 2.2.3:Solution of the well-posed problem given in Eq.(2.1.7),by the primal collocation method,with polynomials as trial functions.O=15 is used in Eq.(2.2.4).16 points are uniformly distributed within 0≤x≤1 for the collocation of the 4th order ODE.

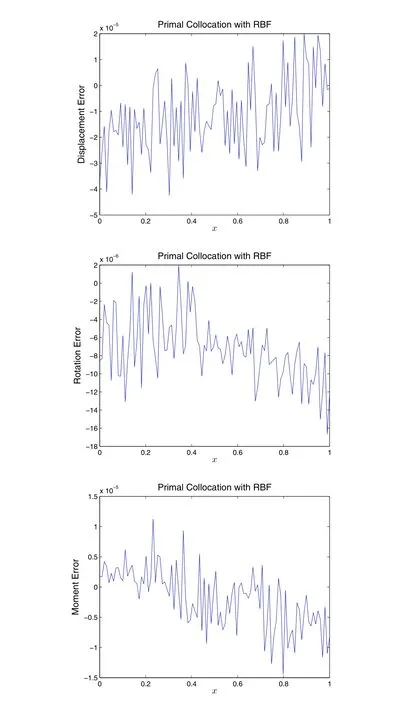
Figure 2.2.4:Solution of the well-posed problem given in Eq.(2.1.7),by the primal collocation method,with global RBFs as trial functions.O=15 is used in Eq.(2.2.5).15 points are uniformly distributed within 0≤x≤1 for the collocation of the 4th order ODE.

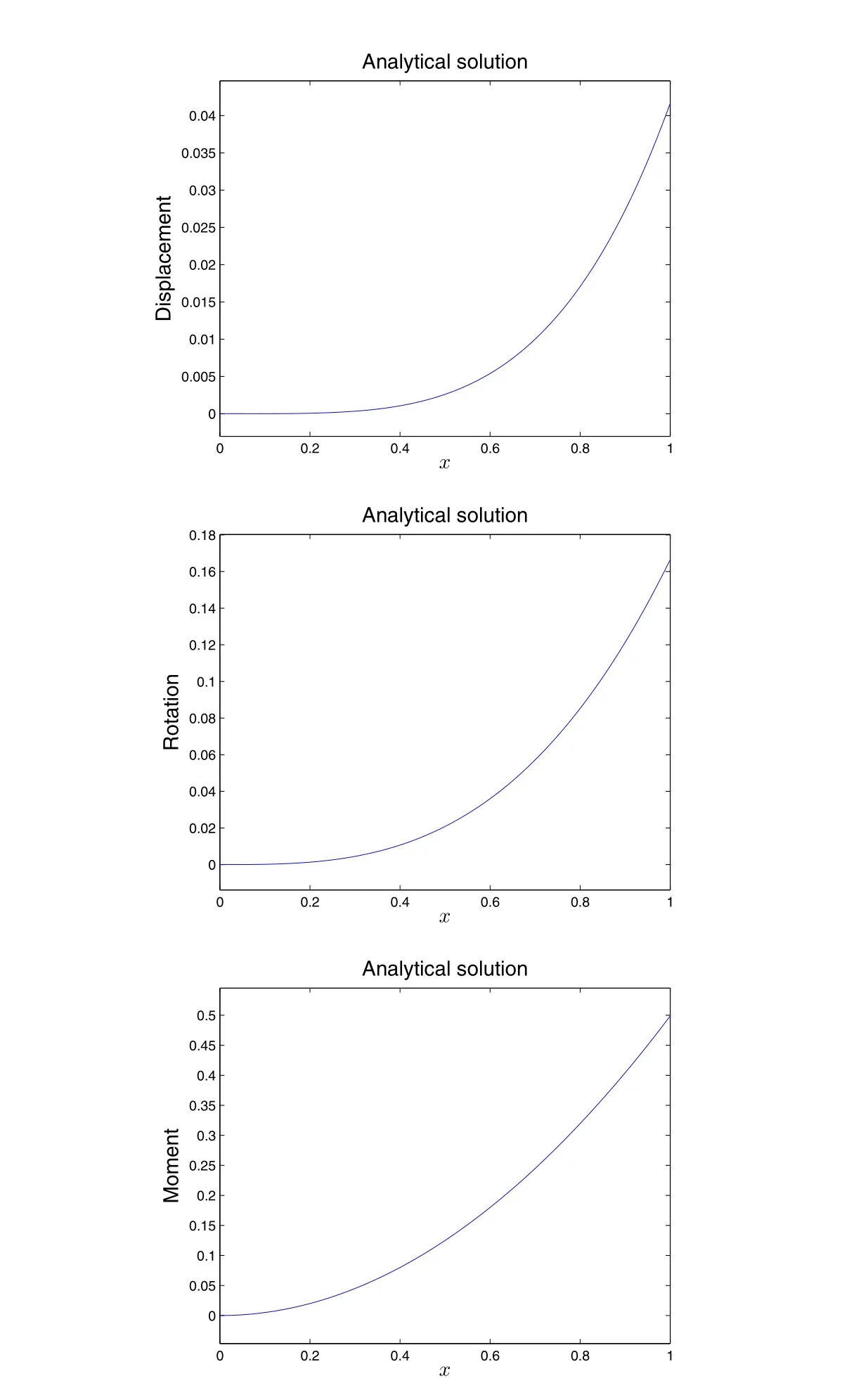
Figure 2.2.5:Analytical solution of the ill-posed problem given in Eq.(2.1.9)

Figure 2.2.6:Solution of the ill-posed problem given in Eq.(2.1.9),by the primal collocation method,with Harmonics as trial functions.O=15 is used in Eq.(2.2.3).31 points are uniformly distributed within 0≤x≤1 for the collocation of the 4th order ODE.

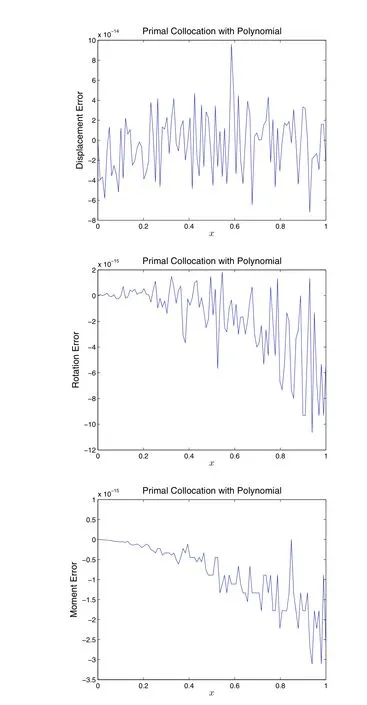
Figure 2.2.7:Solution of the ill-posed problem given in Eq.(2.1.9),by the primal collocation method,with polynomials as trial functions.O=15 is used in Eq.(2.2.4).16 points are uniformly distributed within 0≤x≤1 for the collocation of the 4th order ODE.

Figure 2.2.8:Solution of the ill-posed problem given in Eq.(2.1.9),by the primal collocation method,with global RBFs as trial functions.O=15 is used in Eq.(2.2.5).15 points are uniformly distributed within 0≤x≤1 for the collocation of the 4th order ODE.

Dense Coefficient Matrix:Global interpolations imply that the value of the trial function at each point depends on all the undetermined coefficients.It is thus easy to see that the obtained coefficient matrix by Collocation(or any other method),with Global trial functions should be fully-populated.This is disadvantageous for the storage and solution of the system of equations.

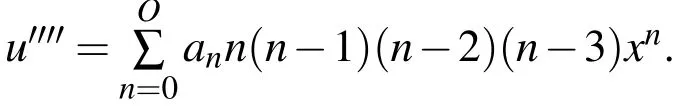
Table 2.2.1:Condition numbers for the coefficient matrices of primal collocation methods,with global Harmonics,Polynomial,RBFs as trial functions.O=15 is used in Eqs.(2.2.3)-(2.2.5)

2.2.3Global trial functions,primal finite volume method

For the weighted-residual weak form Eq.(2.2.2),instead of using Dirac Delta function as the test function,another simple choice is to use the Heaviside function as the test function.This leads to the subdomain method or the finite volume method(FVM).We firstly de fineNsubdomains of the beam: ΩI，I=1，2，...，N,whereΩI⊂Ω.It should be noted that,there is a variety of methods for the definition of subdomains ΩI,which can be either overlapping or non-overlapping.In this study,we simply divide the beamintoNsegments byN+1 points,x0=0，x1，...，xN=1.So that we haveWe denote the boundary of the subdomain as∂ΩI.By considering various boundary conditions,we further denote various parts of the local boundary as:

The Heaviside function for theIthsubdomain(or hat function)is de fined as:

Substituting Eq.(2.2.9)into the weighted-residual weak-form Eq.(2.2.2),we have:

In this way,we are actually enforcing that the average residual of the 4thorder ODE should vanish in each subdomain.By using,and implementing the boundary condition at,the following finite volume weak-formis obtained:

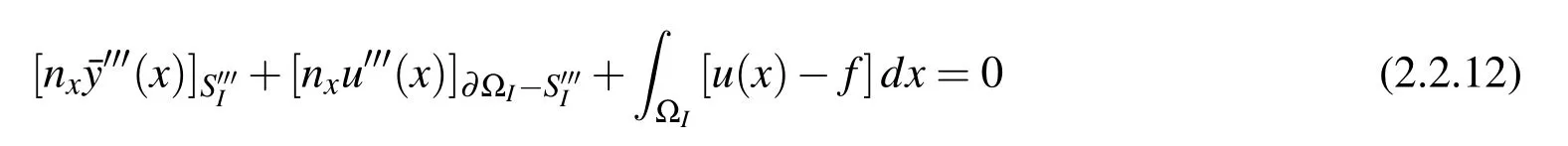
By considering the global trial functions as de fined in Eqs.(2.2.3)-(2.2.6),the finite volume equations for this 4thorder ODE are obtained:

Moreover,the rest of the boundary conditions can be enforced by collocation:

It should be noted that we started from the unsymmetric weak-form Eq.(2.2.2),which involves the 4thorder derivatives of the trial functionu.But the final algorithmic formulations for the primal FVM,asgiven in Eqs.(2.2.13)-(2.2.14),involve only up to the3rdderivatives of the trial function.This,however,doesnot mean that we can reduce the continuity requirement.The trial functions have to be selected fromC3continuous functions for the current primal finite volume method.

We use the primal finite volume method with global interpolations to solve well posed&ill-posed problem given in Eq.(2.1.7)and Eq.(2.1.9).The same global trial functions of Harmonics,Polynomials and RBFs are adopted.The beamis divided into evenly distributedMsubdomains,whereMis equal to the number of undetermined coefficients.It is found that the accuracies of solutions are similar to those primal collocation methods given in section 2.2.2.In order to avoid repetition,only the computational results for global RBF primal FVM are given in Fig.(2.2.9)-(2.2.10).

It can be seen that the simple scheme of the primal FVM can also deal with with both well-posed and ill-posed BCs quite easily.However,the 3 obvious disadvantages of using global trial functions,as discussed in the previous section for primal collocation method,are still the main obstacles that are preventing the applications of these global methods.For this reason,methods with local interpolations are more favorable.

Element-based interpolations,and node-based meshless interpolations are the two most important kinds of local interpolations.For this one-dimensional problem,it is not impossible to developC3elements.Similar to theC1Hermite interpolations,one can develop a two-node interpolation,with 4 DOFsu，u′，u′′，u′′′at each node.However,this type of local interpolation is too complex to be useful.Moreover,generalization of this type of interpolation to arbitrarily-shaped 2D and 3D elements is almost impossible.Therefore,instead of using element-based interpolations,we use meshless interpolations in this study for primal collocation and FVM,which can easily satisfy the requirement ofC3continuity of trial functions.

2.3　Local weighted-residual unsymmetric weak-form-1, meshless local trial functions,MLPG primal collocation& finite volume methods

2.3.1Local unsymmetric weak-form-1

The Meshless Local Petrov Galerkin(MLPG)method is a truly meshless method,without using element-based interpolations,and without involving background elements/cells to evaluate domain integrals[Atluri and Zhu(1998)].The fundamental difference between MLPG, finite elements as well as other Galerkin meshless methods(such as EFG)is that,MLPG is based on local Petrov-Galerkin weak-forms instead of the global symmetric Galerkin weak-form.A variety of primal MLPG methods is available,with various local symmetric&unsymmetric weak-forms,leading to MLPG collocation, finite volume,Galerkin,LBIE,etc,see[Zhu,Zhang,and Atluri(1998a,b);Atluri and Zhu(1998);Atluri,Kim,and Cho(1999);Atluri,Sladek,Sladek,and Zhu(2000);Sladek,Sladek,and Atluri(2000);Sladek,S-ladek,and Zhang(2003);Atluri and Shen(2002a,b);Atluri,Han,and Shen(2003);Atluri(2004)].Systematic treatments of various primal MLPG methods can be found in the monographs[Atluri and Shen(2002a);Atluri(2004)].Several mixed implementations of MLPG approached was also developed in[Atluri,Han,and Rajendran(2004);Atluri,Liu,and Han(2006a,b);Avila,Han,and Atluri(2011)].A detailed review of applications of MLPG for various problems in engineering and applied sciences can also be found in[Sladek,Stanak,Han,Sladek,and Atluri(2013)].

Figure 2.2.9:Solution of the well-posed problem given in Eq.(2.1.7),by the primal finite volume method,with global RBFs as trial functions.O=15 is used in Eq.(2.2.5).The beamis uniformly divided into 15 subdomains to enforce FVM equations of the 4th order ODE.

Figure 2.2.10:Solution of the ill-posed problem given in Eq.(2.1.9),by the primal finite volume method,with global RBFs as trial functions.O=15 is used in Eq.(2.2.5).The beamis uniformly divided into 15 subdomains to enforce FVM equations of the 4th order ODE.

The trial functions of general meshless methods are constructed based on a scatter of nodes:xI，I=1，2，...，N,each of which are associated with a fictitious nodal unknown.Unlike the traditional FEM and various Global Galerkin meshless methods such as EFG[Belytschko and Lu(1994)],for this 4thorder ODE,the weak-form can be obtained by considering a local subdomain ΩIfor each nodexI,and write the weigh-residual integral over this subdomain:

There is a variety of ways of defining the local subdomain ΩI,among which the most convenient and popular one is to consider a local interval centered at nodexI,with a fixed radiuslI,i.e.In this way,the local subdomains ΩIare either over-lapping or non-over-lapping,depending on the prede fined subdomain radiuslI.Similar to what was done for the primal FVM,we denote the boundary of the subdomain as∂ΩI.By considering various boundary conditions,we further denote various parts of the local boundary as:

Integrating Eq.(2.3.1)by parts several times,a variety of different local symmetric and unsymmetric weak-forms can be obtained.Only some of the most useful ones are given in the section 2.3,2.5,2.7,while detailed discussions of each weak-form can be found in[Atluri and Shen(2005,2002b)].

2.3.2Meshless local trial functions

In general,meshless methods use a local interpolation/approximation,to represent the trial function,using the values(or the fictitious values)of the unknown variable at some random ly located nodes.Various meshless interpolations are available in[Atluri and Shen(2002a);Atluri(2004)],such as Moving Least Squares(MLS),compactly-supported Radial Basis Functions(cs-RBF),Shepherd Functions,Partitions of Unity,etc.Detailed discussions of various meshless interpolations are beyond the scope of this study.Only MLS is implemented and demonstrated at here.

The MLS method starts by expressing the variableu(x)as polynomials:

whereis the monomial basis complete to the ordern.In this study,the third-order interpolation is used.a(x)is a vector containing the coefficients of each monomial basis,which can be determined by minimizing the following weighted least square objective function,de fined as:

where,xI，I=1，2，...，N,is a group of discrete nodes,andˆuIis the fictitious nodal value atxI,w I(x)is the preselected weight function.Various weight functions can be found in[Atluri and Shen(2002a);Atluri(2004)].In general,the weight function should be a local function,i.e.it should be non-zero only within a certain support range of nodexI.The weight function should also be positive and continuous up to a certain order.For this case,C3continuity is required.A 7thorder spline weight function is used here:where,rIstands for the radius of the support range for nodexI,anddIstands for the distance betweenxandxI.

From Eq.(2.3.4),the basis function of the MLS can be obtained:

where,matricesA(x)andB(x)are de fined by:

Φ(x)is named as the MLS basis function.It should be noticed that,are named as fictitious nodal values because the MLS interpolation generally does not pass through these values at each scattered node,i.e.

The differentiations of the MLS basis functions,however,are quite complex,by exploring the following relations:

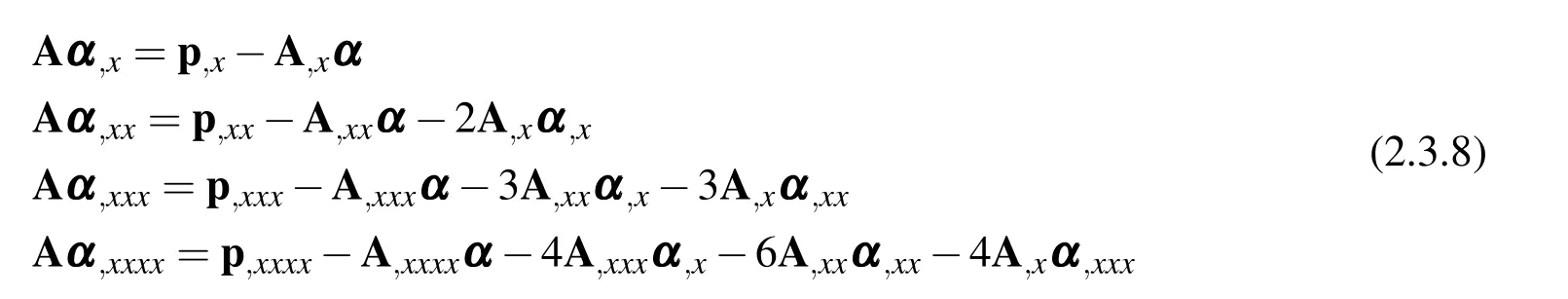
And the derivatives up to the fourth-order are obtained by:

2.3.3MLPG primal collocation method

In a fashion similar to the primal collocation with global interpolations,the MLPG primal collocation can be developed,with Moving Least Squares as trial functions.For example,by usingv=δ(x-xI)as the test function,the local weak-form Eq.(2.3.1)leads to the MLPG primal collocation method:

And the boundary conditions are also enforced by collocation:

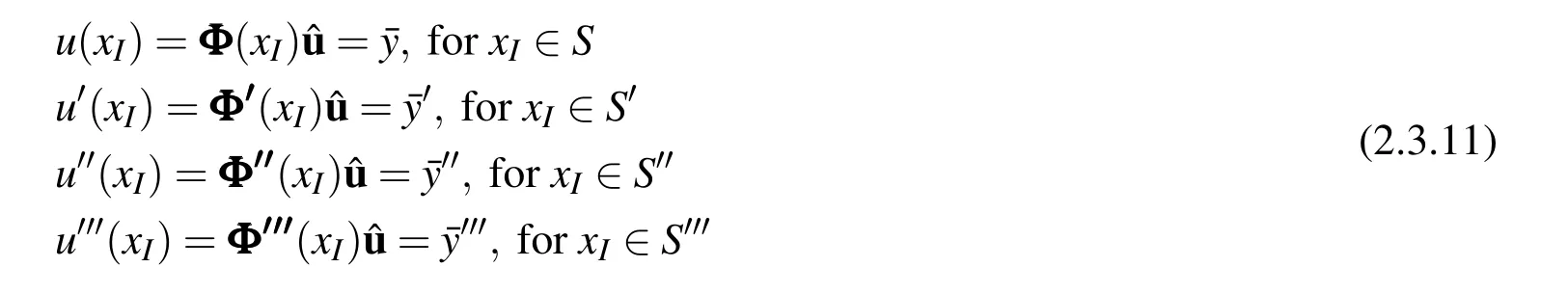
It can be seen that the algorithmic formulation of the current MLPG method is the same as those primal collocation method given in section 2.2.The only difference is that MLS trial functions are used instead of global interpolations.However,through several numerical experiments,it is found that the MLPG primal collocation method with MLS trial functions cannot obtain a meaningful solution for such a 4thorder ODE.For example,we use 15 uniformly distributed nodes in the beam to construct the MLS basis functions,and enforce the 4thorder ODE by collocation at at each node.3.5his used as the radius of support range(rI)of each node,withbeing the nodal distance.Very large computational error for displacement,rotation,and moment are obtained for such a MLPG primal collocation method,as given in Fig.2.3.1.

This is mainly due to the complexity of high-order derivatives of MLS basis functions.To clarify this,with 15 uniformly distributed nodes,we compare the basis functions of MLS to global RBF.In Fig.2.3.2 and Fig.2.3.3,the basis function of the 8thnode(x8=0.5)for both MLS and RBF,as well as their derivatives up to the 4thorder,are given.It can be seen that,although MLS has the favorable feature of locality,its higher-order derivatives are too complex.Therefore,in MLS-based methods,one should avoid using higher-order derivatives of the basis functions.This can be done either through integrations by parts,or using the mixed approaches,as shown later in this study.

2.3.4MLPG primal finite volume method

The MLPG primal finite volume method can be developed,by usingv=1 as the test function for the local unsymmetric weak-form Eq.(2.3.1).Actually,this will lead to exactly the same finite-volume equations as compared to the global finite volume method,i.e.Eq.(2.2.12).The only difference is that MLS basis functions are used instead of global trial functions.Thus,we directly write down the final equations for the MLPG primal finite volume method:

The rest of the boundary conditions can be implemented by collocation:

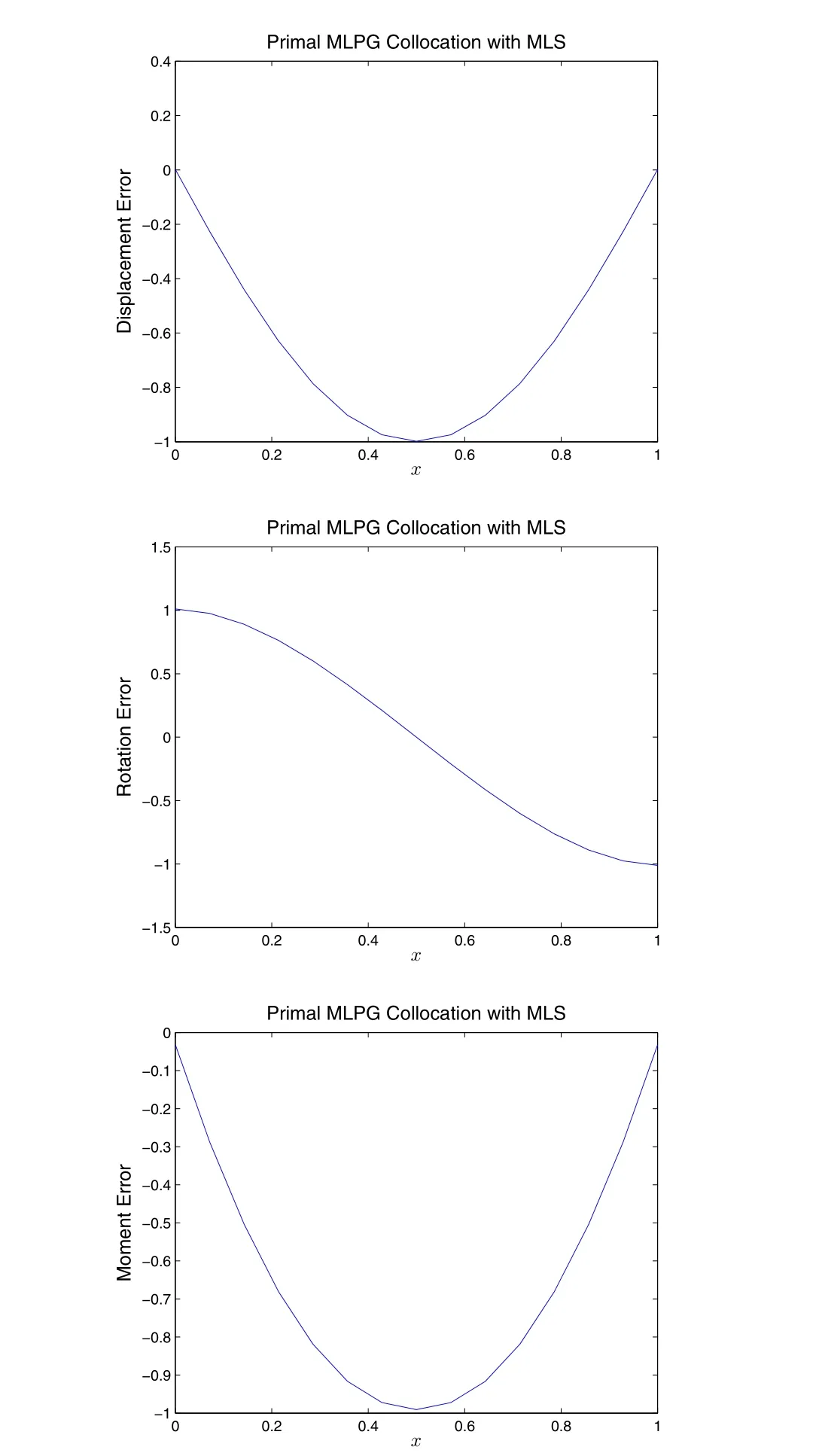
Figure2.3.1:Solution of the well-posed problem given in Eq.(2.1.7),by the MLPG primal collocation method,with MLS as trial functions.15 uniformly distributed nodes are used to construct the MLS basis functions.rI=3.5h are de fined as the radius of the support range associated with each node xI.

Figure 2.3.2:The global RBF function,and its derivatives up to the 4th order

Figure 2.3.3:The local MLS function,and its derivatives up to the 4th order

Figure2.3.4:Solution of the well-posed problem given in Eq.(2.1.7),by the MLPG primal finite volume method,with MLS as trial functions.15 uniformly distributed nodes are used to construct the MLS basis functions. are de fined as the radius of the support range and subdomain associated with each node

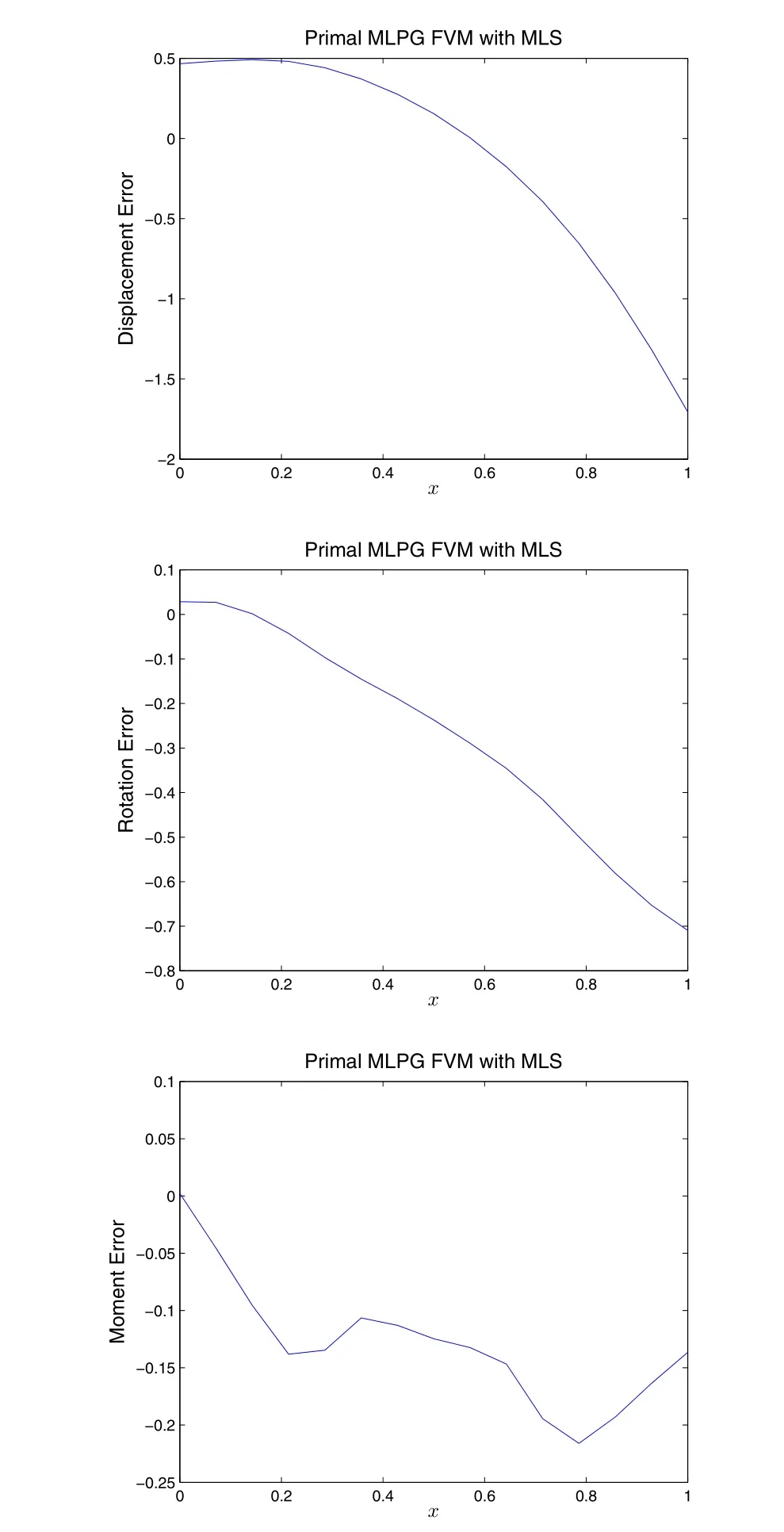
Figure 2.3.5:Solution of the ill-posed problem given in Eq.(2.1.9),by the MLPG primal finite volume method,with MLS as trial functions.15 uniformly distributed nodes are used to construct the MLS basis functions.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node

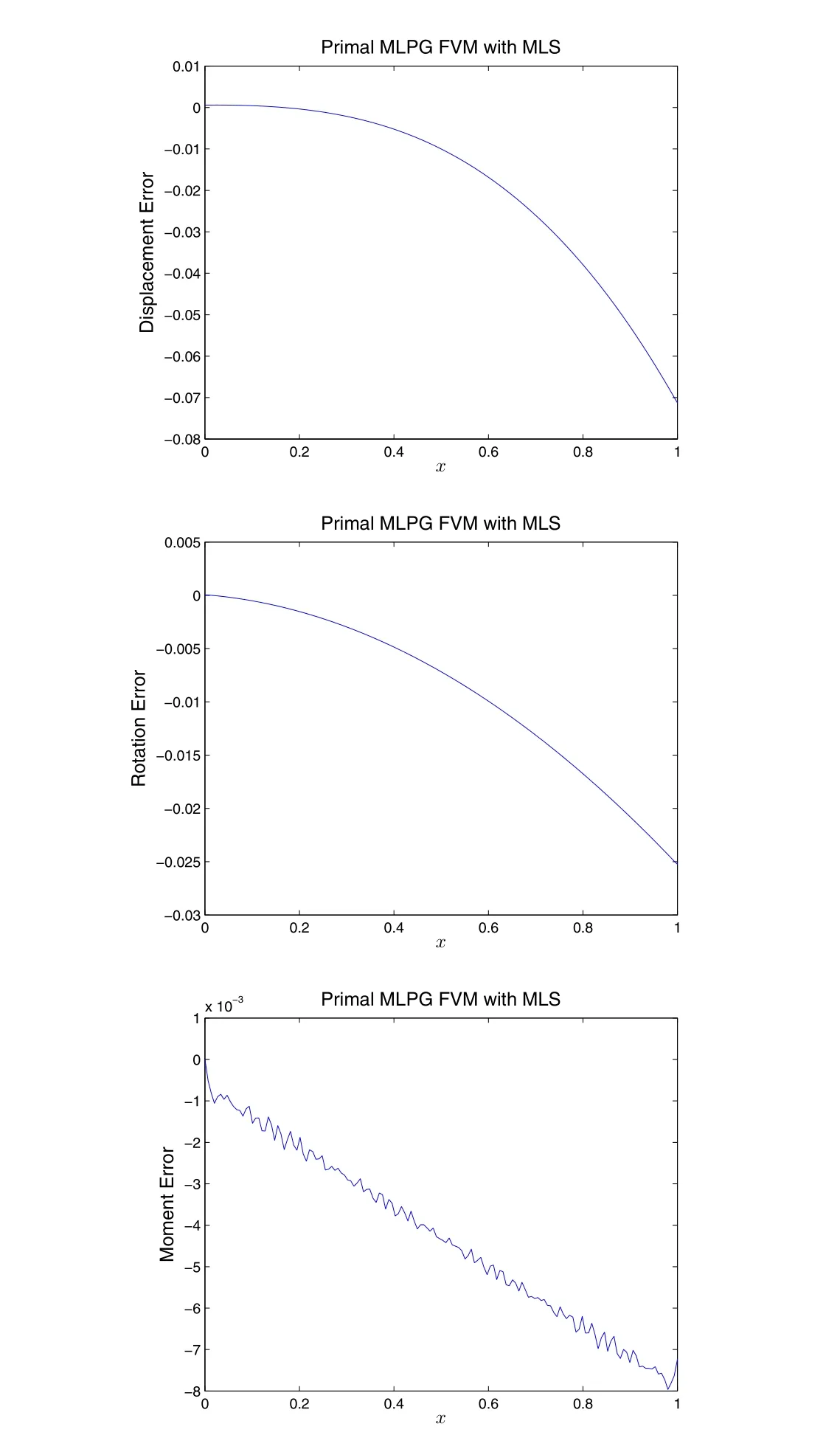
Figure 2.3.6:Solution of the ill-posed problem given in Eq.(2.1.9),by the MLPG primal finite volume method,with MLS as trial functions.150 uniformly distributed nodes are used to construct the MLS basis functions.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node xI.

We use the MLPG primal FVM with MLS to solve well-posed&ill-posed problems given in Eq.(2.1.7)and Eq.(2.1.9).15 uniformly distributed nodes are used to construct the MLSbasis functions.3.5his used as the radius of support range(rI)of each node,withbeing the nodal distance.The radius of the subdomain(lI)is also de fined as 3.5h.As shown in Fig.2.3.4,for the well-posed problem,the MLPG primal FVM can obtain reasonable solution for the well-posed problem,although the accuracy is not highly satisfactory.Comparing this to the failure of MLPG primal collocation method,one can see that this is because the collocation scheme involves the evaluating of the 4thorder derivative of Φ(x)at each collocation point,while the FVM scheme only involves evaluating the 3rdorder derivative of Φ(x)at the local boundary of each subdomain.Therefore,in the development of MLPG methods,one should avoid evaluating higher-order derivatives of Φ(x)as much as possible.From Fig.2.3.5,one can see that the MLPG primal FVM performs worse in solving the ill-posed problem.This is expected because solutions of ill-posed problem are generally unstable,and highly-sensitive to various errors of caused by prescribed boundary conditions,given material parameters,as well as inaccurate computational schemes.The accuracy of the solution can be improved by increasing the number of nodes,as shown in Fig.2.3.5.However,a more efficient&accurate computational scheme is preferred,with mixed formulations instead of primal ones.This will be demonstrated in section 3 and 4.

2.4　Global symmetric weak-form,primal finite element method

2.4.1Global symmetric weak-form

Integrating Eq.(2.2.2)by parts tw ice yields the following global symmetric weak form,

It can be seen in Eq.(2.4.1),higher-order BCsu′′，u′′′are naturally embedded in the symmetric weak-form.Therefore,we can satisfy the higher-order BCs atS′′，S′′′with the symmetric weak-form,and satisfy the lower-order BCs atS，S′a-priori.For the well-posed problems,we have.Therefore,we can prescribe that the test functionsv，v′should vanish atS，S′,in order to simplify the symmetric weak-form.In this way,we satisfy the following conditions a-priori:

And the symmetric weak form becomes:

withnx=-1 atx=0 andnx=1 atx=1.

For this symmetric weak form,both the trial and test function are required to beC1continuous.It is still possible to use global trial functions in terms of Harmonics,Polynomials and RBFs,leading to the global Galerkin method,such as[Dai,Paik,and Atluri(2011)].However,as discussed before,using global trial functions leads to a dense,ill-conditioned system of equations.It is more favorable to have local trial functions instead of global ones.In the next subsection,we use element based trial functions(Hermite Interpolation),and develop the primal Finite Element Method.

2.4.2Hermite interpolation, finite element method

In order to satisfy the requirement ofC1continuity,element-based Hermite interpolations can be used as trial functions.We divide the domain of interest intoNnonoverlapping sub-domains,withN+1 nodesIn this way,each subdomain ΩIcan be de fined asFor finite element method,such non-overlapping subdomains are named as elements.The trial function and test functions are interpolated using the same element-based basis functions:

And finite element equations are obtained by substituting Eq.(2.4.4)into the symmetric weak form Eq.(2.4.3):

which can be rewritten as:

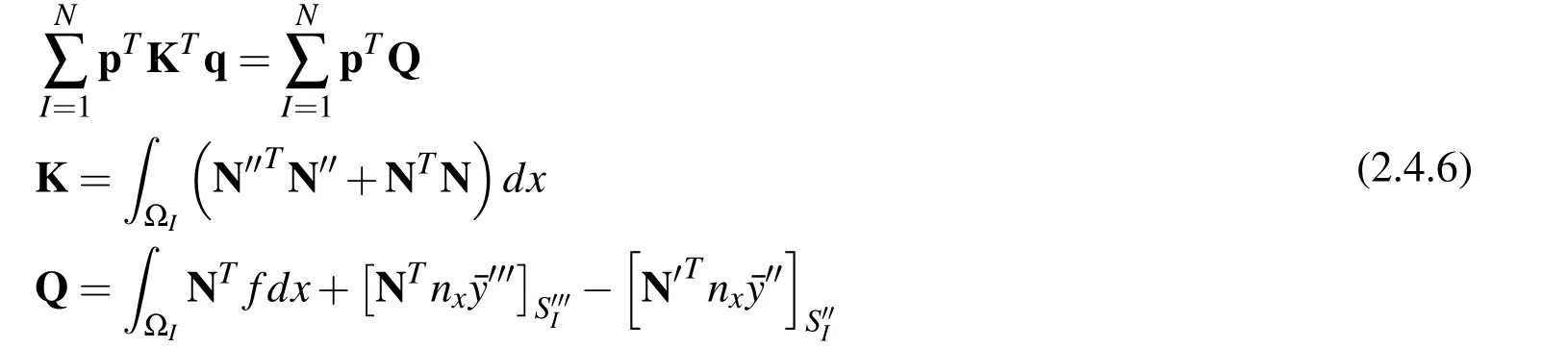
where

This will lead to the global FEM equation by considering the arbitrariness ofp:

andQgare the generalized global stiffness matrix and force vector,obtained by the assembly of their local counterparts for each element.Andqgis the vector of nodal unknowns to be solved.

As an example,this 4thorder ODE is solved using 15 even-sized primal finite elements.As shown in Fig.2.4.1,computational results agree with with analytical solutions.Onecanalso find out that the system of equations aresymmetric,banded,sparse,positive-de finite,and well-conditioned.

However,one should be aware that,althoughC1elements are simple for this one dimensional problem,they are too difficult for generally-shaped,two-and three dimensional problems.Therefore,for higher-order higher-dimensional problems,such as the fourth-order PDE of the Kirchoff plate,it is difficult to use the primal formulation to develop Finite Elements.

Another disadvantage of finite element method is that,it can not directly deal with ill-posed BCs.This is because that the symmetric weak-form cannot accommodate higher-order and lower-order BCs at the same part of the boundary.As shown in Eqs.(2.4.1)-(2.4.3),at a boundary pointx=0 or 1,the test functionvis set to be 0 ifuis prescribed,therefore the high-order BC ofu′′′cannot be prescribed at the same boundary point.Similarly,u′andu′′cannot be prescribed at the same boundary point.

2.5　Local symmetric weak-form,MLPG method

2.5.1Local symmetric weak-form

For the MLPG method,a local subdomain ΩIis associated with each of the scattered nodes:xI，I=1，2，...，N.Similar to the global weak-form Eq.(2.4.1),the same equation can be written for each subdomain:

As shown in Eq.(2.2.9),various parts of the local subdomain can be denoted asAnd for well-posed problems,we haveThus,by substituting in the higher-order boundary conditions in Eq.(2.5.1),the following local symmetric weak-form can be obtained:

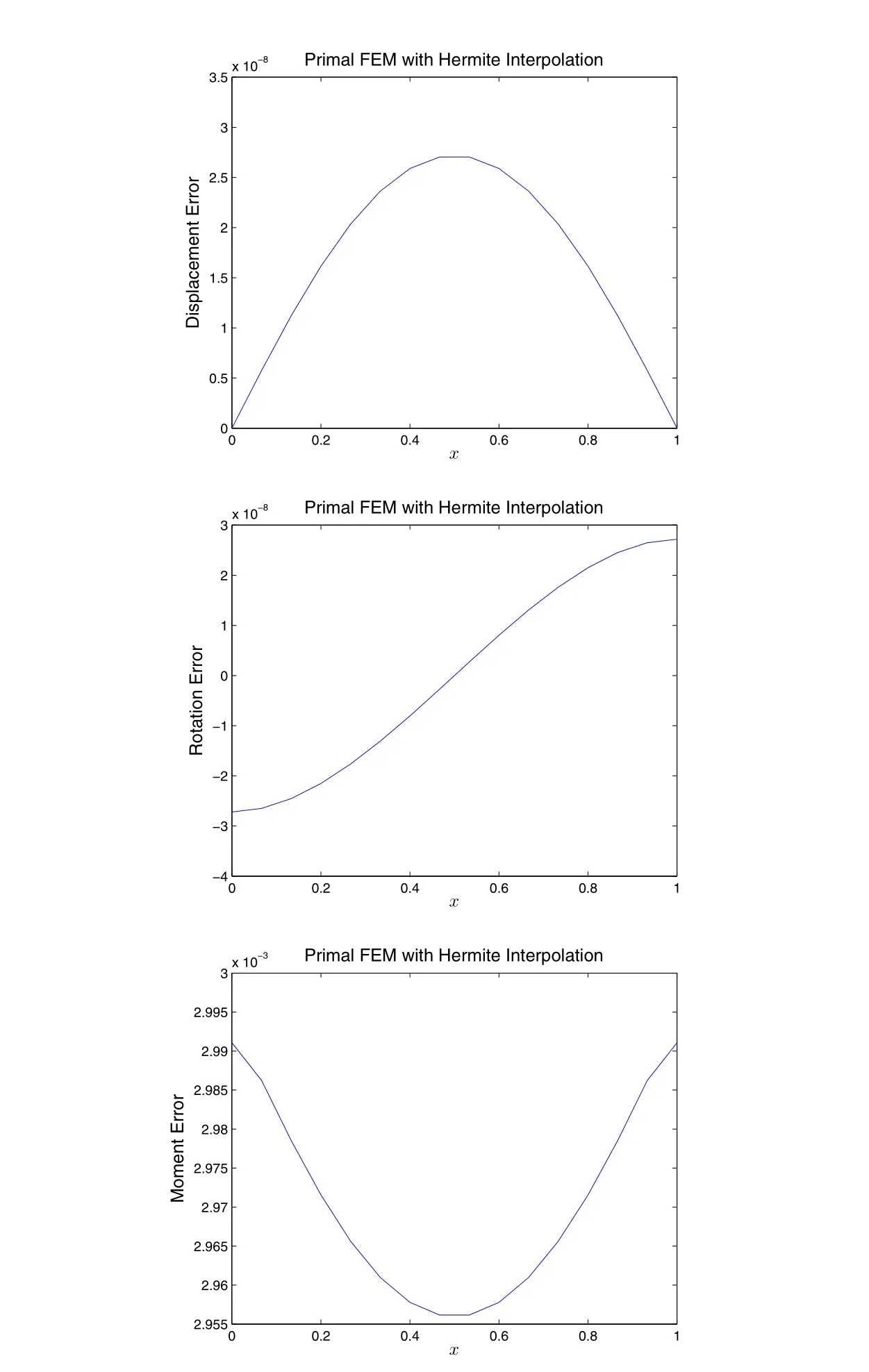
Figure 2.4.1:Solution of the well-posed problem given in Eq.(2.1.7),by the primal finiteelement method,withelement-based Hermite interpolations astrial functions.15 even-sized elements are used for the discretization of the beam.

In order to further simplify the weak-form, and avoid evaluating higher-order derivatives of MLS basis functions as much as possible, we can select special test function such thatvandv′should vanish atLI.In this way,Eq.(2.5.2)becomes:

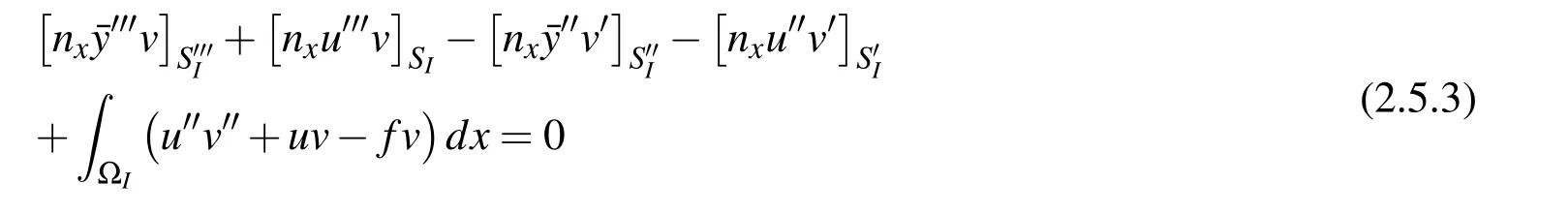
2.5.2MLS weight-function as the test function,MLPG primal method

In this section,we develop MLPG method for this 4thorder ODE,based on the symmetric weak-form Eq.(2.5.3).As discussed in last section,the test function should be selected so thatvandv′vanish atLI.As shown in section 2.3.2,the weight-function for MLS is such a function.Suppose the radius of the local subdomain islI,we can use the following 7thorder spline function as the test function:

wheredIis the distance betweenxand nodexI.

By using MLS as the trial functions,the following equations of MLPG can be obtained:

And the lower-order BCs are enforced by simple collocation:

We use the current MLPG method to solve the well-posed problem given in Eq.(2.1.7).15 uniformly distributed nodes are used to construct the MLS basis functions.3.5his used as the radius of support range(rI)of each node,withbeing the nodal distance.The radius of the subdomain(lI)is also de fined as 3.5h.As shown in Fig.2.5.1,for the well-posed problem,the current MLPG method is much more accurate than the MLPG primal collocation and finite volume method.This is because,by using the symmetrical weak-form,only the 2ndorder derivatives ofuinside the beam,and up to the 3rdorder derivatives ofuat the global boundary are involved.However,the current MLPG method,with symmetric weak-form are unsuitable for solving ill-posed problems.The mixed MLPG methods are more favorable for solving ill-posed problems,which will be demonstrated in section 3 and 4.

Figure2.5.1:Solution of the well-posed problem given in Eq.(2.1.7),by theMLPG method using symmetric local weak form,with MLS as trial functions,and MLS weight function as test functions.15 uniformly distributed nodes are used to construct the MLS basis functions.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node xI.

2.6　Global unsymmetric weak-form-2,boundary integral equations,boundary element methods

2.6.1Global Unsymmetric weak-form-2,and non-singular BIE for u

Integrating Eq.(2.4.1)by parts for another two times yields the following unsymmetric weak form,

In this weak form,no derivatives of the trial function appear in the domain integral,so there is no continuity requirement for the trial functionu.One the other hand,the test functionvshould beC3continuous.If we choose the test function as the fundamental solution of an in finite beam on an elastic foundation,i.e.v′′′′+v=δ(x-η),withηbeing the source point,then Eq.(2.6.1)is reduced to the boundary integral equation:

with

It should be noted that,in Eq.(2.6.2),all of′，′′，′′′，′′′′represent differentiations with respect tox.

For this 4thorder ODE,The fundamental solution can be easily found by Mathematica:

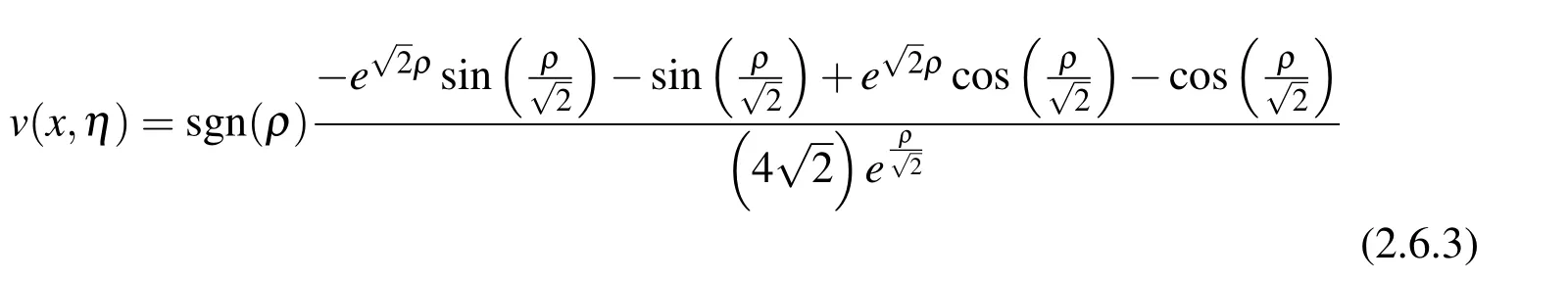
whereρ=x-η.It can also be seen from Fig.(2.6.1)thatv(x，η)has non-singular derivatives up to the 3rdorder.Thus,all the domain and boundary integrals in Eq.(2.6.2)are non-singular.We refer to Eq.(2.6.2)as the non-singular boundary integral equation(BIE)foru.

Figure 2.6.1:Fundamental solution for this 4th order ODE,to be used by BEM,as de fined by Eq.(2.6.3),with the source point located at η=0.5

2.6.2Non-singular BIEs for u′，u′′,&u′′′

If we directly differentiate Eq.eq2.6.2 with respect toη,we can obtain the boundary integral equation for.However,this will involve the 4thorder derivative of the fundamental solutionv,which is singular at the source point.In another way,following the work of[Okada,Rajiyah,and Atluri(1988);Okada,Rajiyah,and Atluri(1989);Han and Atluri(2003);Dong and Atluri(2012c,2013c)],we usev′(x，η)as the test function.Consider the equationand integrate the first term by parts 3 times,integrate the second term by parts once,we obtain the non-singular BIE foru′:

Similarly,consider the equation,integrate the first term by parts tw ice,and integrate the second term by parts tw ice,we obtain the nonsingular BIE foru′′:

2.6.3Boundary element method and dual boundary element method

In Eqs.(2.6.4)-(2.6.6),trial functions only appear in the boundary of the integral equations.This thus will lead to the so-called boundary element method.For this one-dimensional problem,we do not even need elements since the boundary of the beam consists of only two points.There are 4 unknowns for each point ofx=0，1,asu，u′，u′′,andu′′′.No matter it is well-posed or ill-posed problem,there will be 4 boundary conditions.So one simply needs to use two of BIEs foru，u′，u′′,andu′′′at each boundary point.This will make 8 equations for 8 unknowns.

However,the selection of BIEs has some degrees of arbitrariness.If BIEs for lower-order BCs are to be used(u，u′),it leads to the traditional boundary element method.And if BIEs for higher-order BCs are to be used(u′′，u′′′),it leads to the dual boundary element method.Both of these two kinds of BEMs are used to solve the well-posed as well as the ill-posed problems.In Fig.(2.6.2)-(2.6.5),it is shown that both of these two methods can obtain highly accurate solutions.

2.7　Local unsymmetric weak-form-2, local boundary integral equation,MLPGLBIE method

2.7.1Local unsymmetric weak-form-2,non-singular local BIE for u

As discussed before,for the MLPG method,a local subdomain ΩIis associated with each of the scattered nodes:xI，I=1，2，...，N.Similar to the global unsym-metric weak-form-2,the same equation can be written for each subdomain:

Figure 2.6.2:Solution of the well-posed problem given in Eq.(2.1.7),by BEM.

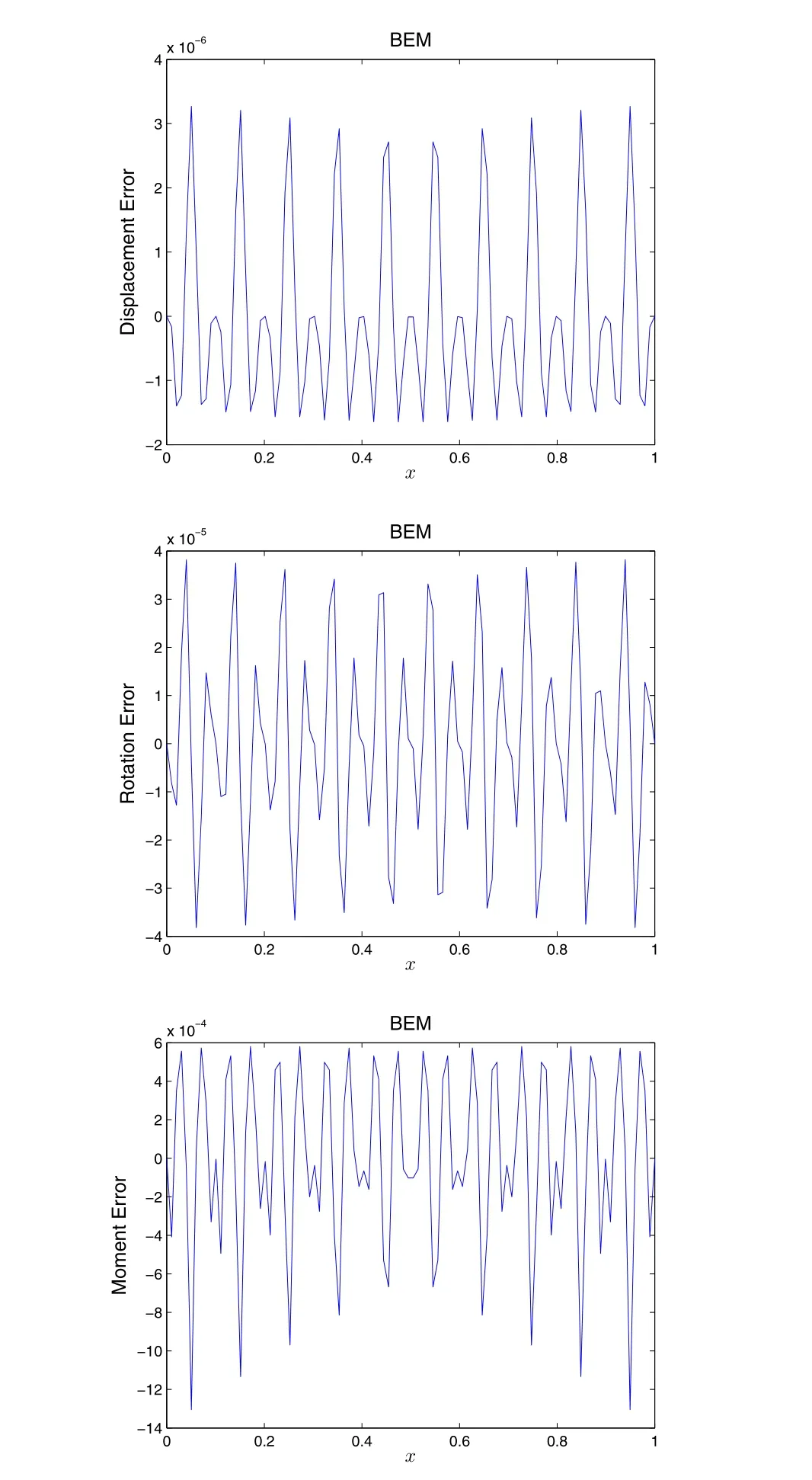
Figure 2.6.3:Solution of the ill-posed problem given in Eq.(2.1.9),by BEM.

Figure 2.6.4:Solution of the well-posed problem given in Eq.(2.1.7),by dual BEM.

Figure 2.6.5:Solution of the ill-posed problem given in Eq.(2.1.9),by dual BEM.

If we choose the fundamental solution of an in finite beam on an elastic foundation as the test function,a local BIE similar to Eq.(2.6.2)can be obtained.However,as discussed before,for MLPG methods,one should avoid evaluating higher-order derivatives ofuas much as possible.Therefore,we select the fundamental solution of an simply-supported beam on an elastic foundation as the test function,i.e.:

Such a test function can be found as:

whereandlIis radius for subdomain ΩI.It can also be seen from Fig.(2.7.1)thatv(x，xI)has non-singular derivatives up to the 3rdorder.With such as test function,vandv′vanish atLI,and Eq.(2.7.1)is reduced to:

Figure 2.7.1:Fundamental solution for the MLPG-LBIE method,as de fined by Eq.(2.7.4),with the source point located at xI=0.5,and the radius of subdomain to be lI=3.5/14.

where

Eq.(2.7.4)can obvious accommodate any BCs foru，u′，u′′，u′′′.Similar to previous MLPG methods,various parts of the local subdomain can be denoted asAnd for well-posed problem,we haveThe following local BIE can be obtained by substituting BCs in to Eq.(2.7.3):

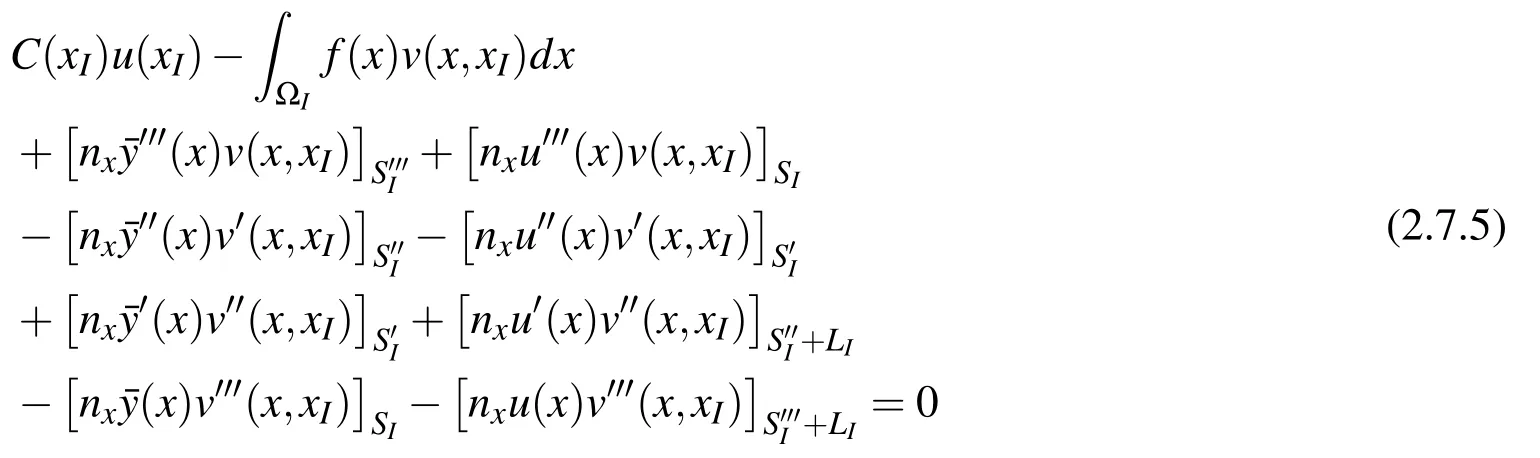
It can be seen that all the integrals in Eq.(2.7.4)is non-singular,and evaluations ofu′′andu′′′are avoided inside the beam.This equation can be used to develop MLPG-LBIE method,as demonstrated in the next section.

2.7.2MLPG-LBIE method

By using MLS as the trial functions,Eq.(2.7.4)leads to the following formulation of the MLPG-LBIE method:

We use the current MLPG-LBIE method to solve the well-posed problem given in Eq.(2.1.7).15 uniformly distributed nodes are used to construct the MLS basis functions.3.5his used as the radius of support range(rI)of each node,withbeing the nodal distance.The radius of the subdomain(lI)is also de fined as 3.5h.As shown in Fig.2.7.2,for the well-posed problem,accurate solution is obtained by the current MLPG-LBIE method.Comparing Fig.2.7.2 to Fig.2.5.1,it can be seen that the accuracy of the MLPG-LBIE method is similar to the MLPG method by using the symmetric local weak-form.However,by using the current MLPGLBIE method,the burden of domain integral is greatly reduced.

Theoretically speaking,thecurrently MLPG-LBIE method canalsobe re-formulated with Eq.(2.7.4)to directly obtain the solution of the ill-posed problem.However,through several numerical experiments,it is found that the accuracy of MLPGLBIE method in solving ill-posed problems is similar to the MLPG primal Finite Volume Method,which are not highly-satisfactory.It is more favorable to use the mixed MLPG schemes to solve the ill-posed problem,as demonstrated in the following two sections.

Figure 2.7.2:Solution of the well-posed problem given in Eq.(2.1.7),by the MLPG-LBIE method,with MLS as trial functions,and MLS weight function as test functions.15 uniformly distributed nodes are used to construct the MLS basis functions.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node xI.

2.8　Trefftz method and method offundamental solutions

2.8.1General solutions of the differential equation,Trefftz method

All the methods presented in the previous sections are based on the concept of weighted-residual weak-forms.Various global and local trial functions are made to satisfy the governing differential equation in a weak-sense through various symmetric and unsymmetric weak-forms.However,for many important engineering problems,general solutions can be found for the governing ODEs/PDEs.If we use the general solutions of the governing differential equation as the trial functions,i.e.satisfying the differential equation exactly,then only boundary conditions need to be enforced,without using any of the previous weak-forms of the differential equation.This lead to the Trefftz method,as firstly introduced by[Trefftz(1926)].Trefftz methods have been applied to solve various engineering problems[Zieli´nski and Herrera(1987);Kita and Kamiya(1995)],with significant advantages for in finite domain acoustics/electromagnetic[Pluymers,Van Hal,Vandepitte,and Desmet(2007);Cheung,Jin,and Zienkiew icz(1991)],micromechanics of materials[Dong and Atluri(2012e,a,b);Bishay and Atluri(2014)],inverse problems[Dong and Atluri(2012d);Liu(2008);Yeih,Liu,Kuo,and Atluri(2010)].

For linear ODE/PDE,the solution is the linear combination of two parts:

withuhbeing the homogeneous part andupbeing the particular solution.

For this simple 4thorder ODE,it is obvious that the homogeneous solution can be generally expressed as:

And for a constant load,the particular solution can be easily found as.

With the trial function given in Eq.(2.8.1)-(2.8.3),the four unknown coefficients can be determined by enforcing the set of 4 BCs,no matter it is a well-posed or ill-posed problem.In this study,the current Trefftz method is used to solve the well-posed as well as the ill-posed problems.In Fig.(2.8.1)-(2.8.2),it is shown that highly accurate solutions are obtained.

The main disadvantage of Trefftz method is that,general solutions are only available for simple linear problems.It is difficult to find complete trial functions which exactly satisfy nonlinear differential equations.Even for linear problems of multiphysics such as piezoelectricity,the general solutions become very complex,see[Bishay and Atluri(2014)].Moreover,Trefftz method,as a type of global method,also leads to dense and ill-conditioned coefficient matrices,which necessiate special treatments such as the scaling method proposed by[Liu(2008)].

2.8.2Method offundamental solutions

Instead of using general solutions as trial functions,the Method of Fundamental Solutions(MFS)expresses the trial function(the homogeneous part)as a linear combination offundamental solutions:

where the fundamental solution was given in section 2.6.1:

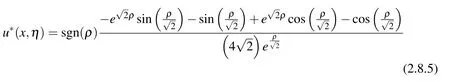
withρ=x-η.And in order to make sure the governing differential equation is exactly satisfied forx∈Ω,the source points should be placed outside of the beam.Comparing Eq.(2.8.5)to Eq.(2.8.2),one can readily see that,if we select 4 source pointsη1，η2，η3，η4,which are placed outside the beam,the two expressions for the Trefftz method and the MFS are entirely equivalent.The relations between MFS and Trefftz trial functions for higher-dimensional problems of Laplace equation,Biharmonic equation and linear elasticity were also discussed in[Chen,Wu,Lee,and Chen(2007);Dong and Atluri(2012d);Yeih,Liu,Kuo,and Atluri(2010)].In this study,we place the four source points at,and solve both the well-posed and ill-posed problems using MFS.As clearly shown in Fig.(2.8.3)-(2.8.4),highly accurate solutions are obtained for both well-posed and ill-posed BCs.

Figure2.8.1:Solution of the well-posed problem given in Eq.(2.1.7),by the Trefftz method.

Figure 2.8.2:Solution of the ill-posed problem given in Eq.(2.1.9),by the Trefftz method

Figure 2.8.3:Solution of the well-posed problem given in Eq.(2.1.7),by the method offundamental solutions.

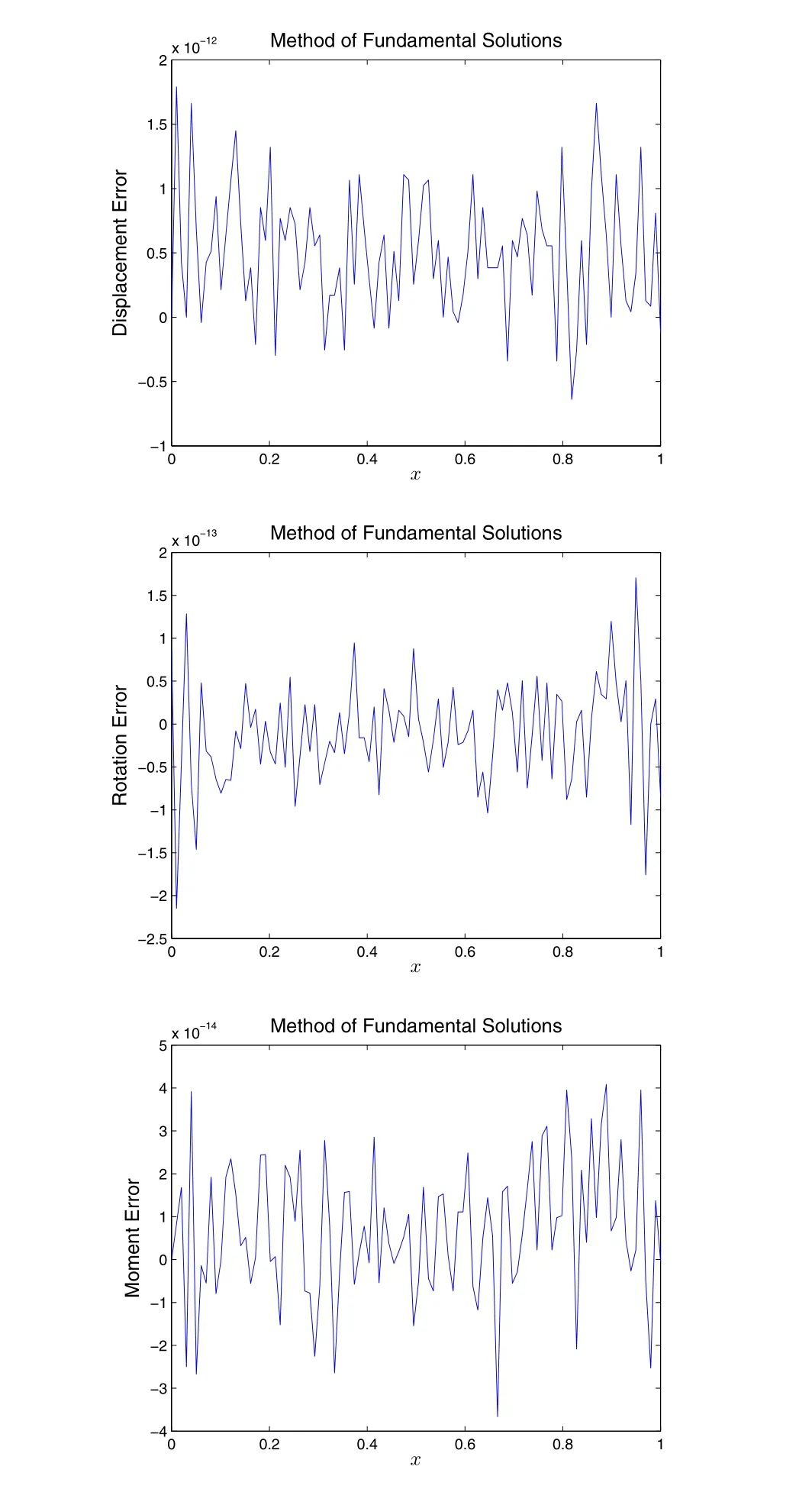
Figure 2.8.4:Solution of the ill-posed problem given in Eq.(2.1.9),by the method offundamental solutions

3　The first kind of mixed methods

3.1　Mixed-1 formulation and the corresponding weak-form

For this 4thorder ODE,there are at least two approaches to develop the mixed formulations.In this section,the first kind of mixed methods are demonstrated.In this method,uas well as its second-order derivativemare treated independently as mixed variables.The 4thorder ODE Eq.(2.1.1)is rewritten as a system of two 2ndorder ODEs:

Or equivalently,we can write down its matrix-vector form:

Considering the vector test functionV,the weighted residual weak-form of Eq.(3.1.2)can be obtained:

Comparing Eq.(3.1.2)to Eq.(2.2.2),it is found that by using the mixed formulation,the required continuity of the trial function is reduced fromC3toC1,while the requirement on the test function remains the same.Thus,the current mixed formulation allows us to useC1element-based interpolations[Hermite interpolation of Eq.(2.4.4)],or meshless local interpolations[MLS of Eq.(2.3.3)-(2.3.9)],to develop mixed collocation or finite volume method.As shown in section 2.2 and section 2.3,for collocation and FVM,using global or local weak-forms does not make any difference.Therefore,we use the global weak-form Eq.(3.1.3)through out this section.

3.2　Hermite interpolation,mixed-1 collocation and finite volume methods

Similar to what was done for FEM,we divide the domain of interest intoNnonoverlapping sub-domains,with.And the sameHermite interpolation can be used to independently interpolateuandm:

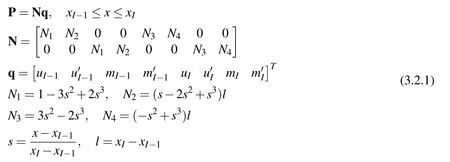
With this formulation,we have 4 unkownsat each node,which add up to 4(N+1)unknowns in all.Therefore,with the set of two second-order ODEs,we need at least 2 collocation points or 2 FVM subdomains in each element.Combined with 4 additional equations for boundary conditions,we will have 4(N+1)equations for 4(N+1)unkowns.

Therefore,we can collocate at the following 2 points within each element:

leading to the following collocation equations:

Similarly,we can divide each element into 2 FVM subdomains:

leading to the following FVM equations:

And boundary conditioned can also be enforced by collocation,in a similar fashion to that of primal methods:

In Fig(3.2.1)-(3.2.4),the mixed-1 collocation and FVM method based on Hermite interpolation,are used to solve the well-posed and ill-posed problems.It can be clearly seem that excellent accuracy was obtained for both the well-posed and ill posed problems.

3.3　MLPG mixed-1 collocation and finite volume methods

Instead of using Hermite interpolations,one can use meshless local interpolations,such as the Moving Least Squares,to approximate bothuandmindependently.With scattered nodes:xI，I=1，2，...，N,the trial functions foruandmcan be expressed in terms of fictitious nodal values,with the same MLS basis functions:

which is equivalent to:

Thus,for each node,there are 2 unknownsandWith the set of two secondorder ODEs,one can simply collocate at each note,leading to the following collocation equations:

Alternatively,one can de fine a local subdomain associated with each node:ΩI={x|xI-lI≤x≤xI+lI，x∈Ω},and use Heaviside function as the test function,to develop MLPG mixed FVM:

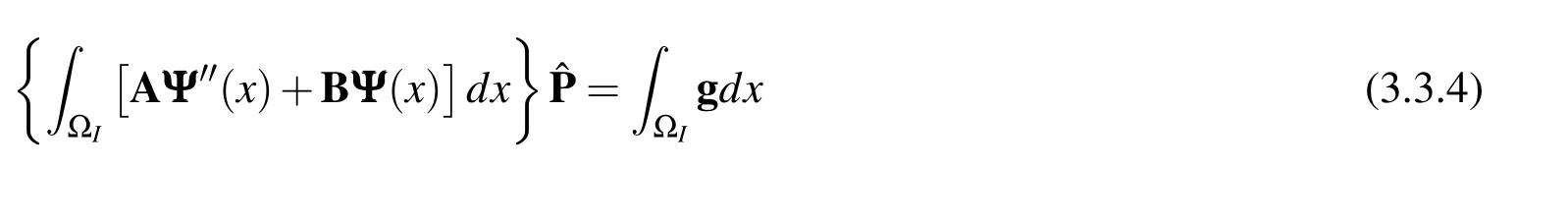
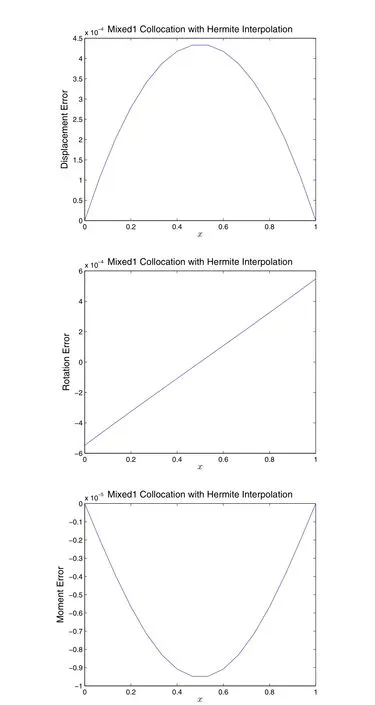
Figure 3.2.1:Solution of the well-posed problem given in Eq.(2.1.7),by mixed-1 collocation method,with element-based Hermite interpolations.15 C1 elements are used.

Figure 3.2.2:Solution of the ill-posed problem given in Eq.(2.1.9),by mixed-1 collocation method,with element-based Hermite interpolations.15 C1 elements are used.Two collocation points are used in each element.

Figure 3.2.3:Solution of the well-posed problem given in Eq.(2.1.7),by mixed-1 finite volume method,with element-based Hermite interpolations.15 C1 elements are used.Each element is divided into 2 FVM subdomains.

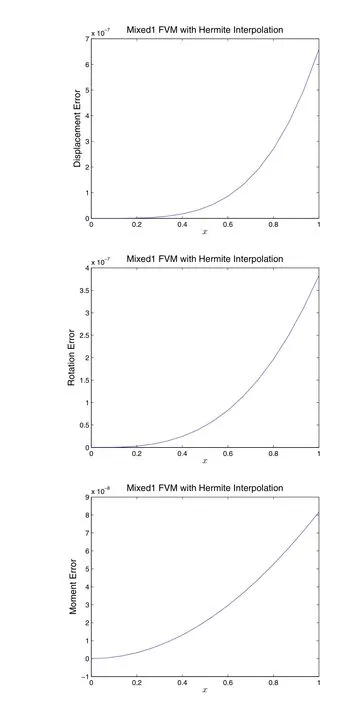
Figure 3.2.4:Solution of the ill-posed problem given in Eq.(2.1.9),by the mixed-1 finite volume method,with element-based Hermite interpolations.15 C1 elements are used.Each element is divided into 2 FVM subdomains.

And boundary conditioned can be enforced by collocation:

In Figs.(3.3.1)-(3.3.4),the current MLPG mixed collocation and FVM are used to solve the well-posed and ill-posed problems.Comparing Figs.(3.3.1)-(3.3.4)to Fig.(2.3.1)and Fig.(2.3.4),it is clearly shown that,with node-based meshless local interpolations as trial functions,mixed collocation and FVM are much better than primal ones.This is due to the complexity of higher-order derivatives of MLS basis functions,as shown in Fig(2.3.3).It can also been seen that,among the current two methods,the MLPG mixed-1 FVM is more accurate than the MLPG mixed-1 collocation method.

4　The second kind of mixed methods

4.1　Mixed-2 formulation and the corresponding weak-form

In the first kind of mixed methods,second-order derivatives of ofuandmare still necessary.This thus requires the usage ofC1elements or MLS interpolations.As discussed before,C1element for higher-dimensional problems are too difficult.Higher-order differentiations of MLS basis functions also significantly increase the computational burden and reduce the accuracy of solution.In the second kind of mixed methods,we treat displacementu,rotationθ,momentm,shearqall as independent variables.The 4thorder ODE is therefore rewritten as:

Or equivalently,we can write down its matrix-vector form:

Figure 3.3.1:Solution of the well-posed problem given in Eq.(2.1.7),by MLPG mixed-1 collocation method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h is de fined as the radius of the support range associated with each node xI.

Figure 3.3.2:Solution of the ill-posed problem given in Eq.(2.1.9),by MLPG mixed-1 collocation method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h is de fined as the radius of the support range associated with each node xI.

Figure 3.3.3:Solution of the well-posed problem given in Eq.(2.1.7),by MLPG mixed-1 finite volume method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node

Figure 3.3.4:Solution of the ill-posed problem given in Eq.(2.1.9),by the MLPG mixed-1 finite volume method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node

Considering the vector test functionW,the weighted residual weak-form of Eq.(4.1.2)can be obtained:

4.2　Linear interpolation,mixed-2 collocation and finite volume method

By rewriting one fourth-order ODE as a system offour first-order ODEs,the required continuity of the trial function is further reduced toC0.This allow us to use simpleC0elements(linear interpolation)to independently interpolateu，θ，m，q.We divide the domain of interest intoNnon-overlapping sub-domains,withN+1 nodesx0=0，x1，x2，...，xN=1.And the trial function can be expressed as:

With this formulation,we have 4 unkowns(uI，θI，mI，qI)at each node,which add up to 4(N+1)unknowns in all.Therefore,with the set of 4 first-order ODEs,we need only 1 equation for each element.Combined with 4 additional equations for boundary conditions,we will have 4(N+1)equations for 4(N+1)unkowns.

Therefore,we can collocate at the following mid-point within each element,leading to the following collocation equations:

Alternatively,we can use Heaviside function in each element as the test function,leading to the following FVM equations:

with ΩIde fined as{x|xI-1≤x≤xI}.

Boundary conditioned can be enforced by collocation:

In Fig(4.2.1)-(4.2.4),the mixed-2 collocation and FVM method based on linear interpolations,are used to solve the well-posed and ill-posed problems.It can be clearly seen that excellent accuracy is obtained for both the well-posed and ill posed problems.

4.3　MLPG mixed-2 collocation and finite volume methods

Alternatively,mesh less local interpolations(MLS)can be used to construct the trial functions ofu，θ，m，qindependently:

which is equivalent to:

Thus,for each node,there are 4 unknownsW ith the set of 4 first-order ODEs,one can simply collocate at each note,leading to the following collocation equations:

Alternatively,one can de fine a local subdomain associated with each node:ΩI={x|xI-lI≤x≤xI+lI，x∈Ω},and use Heaviside function as the test function,to develop MLPG mixed FVM:

Figure 4.2.1:Solution of the well-posed problem given in Eq.(2.1.7),by mixed-2 collocation method,with element-based linear interpolations.15 C0 elements are used.One collocation point is used in each element.

Figure 4.2.2:Solution of the ill-posed problem given in Eq.(2.1.9),by mixed-2 collocation method,with element-based linear interpolations.15 C0 elements are used.One collocation point is used in each element.

Figure 4.2.3:Solution of the well-posed problem given in Eq.(2.1.7),by mixed-2 finite volume method,with element-based linear interpolations.15C0 elements are used.One collocation point is used in each element.

Figure 4.2.4:Solution of the ill-posed problem given in Eq.(2.1.9),by the mixed-2 finite volume method,with element-based linear interpolations.15C0 elements are used.One collocation point is used in each element.

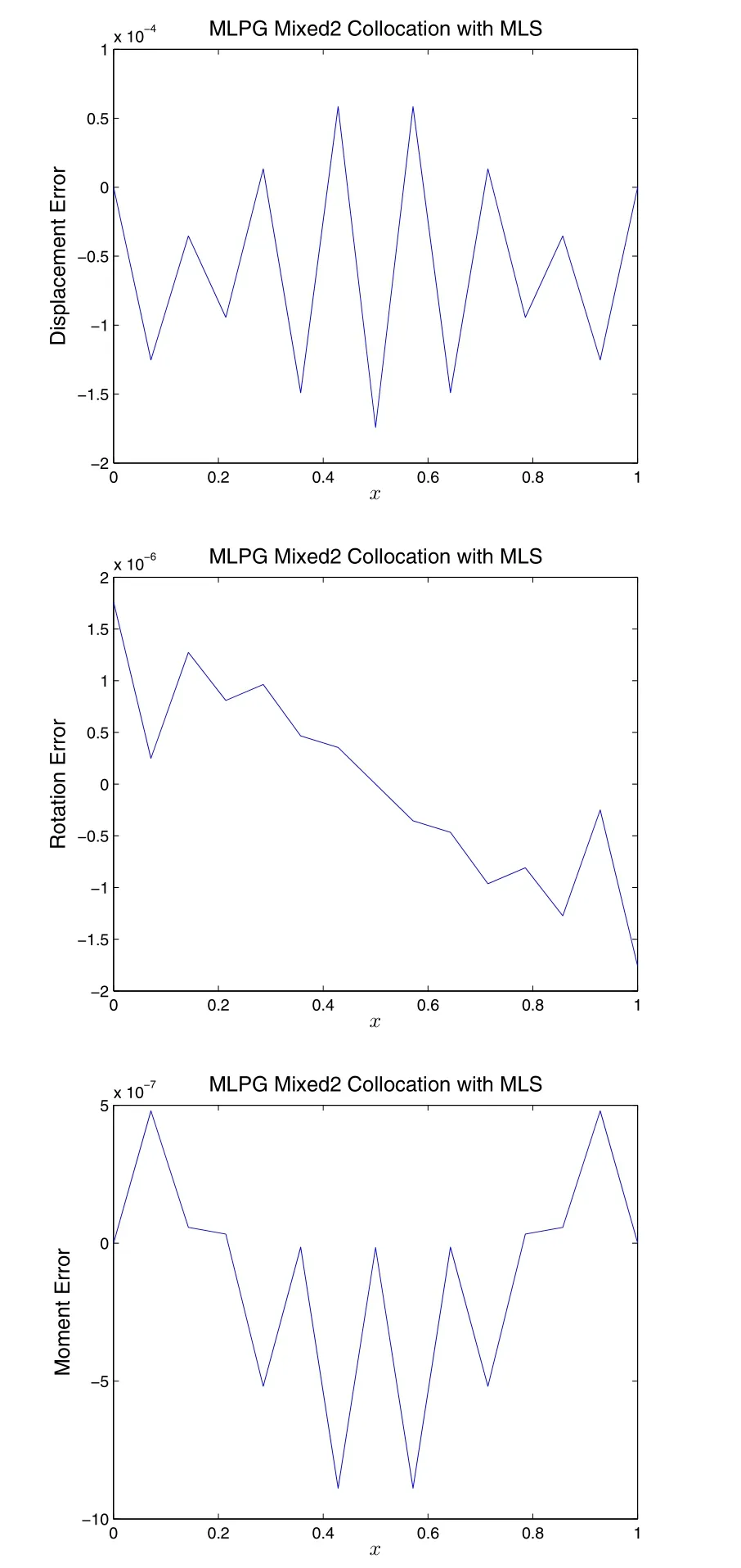
Figure 4.3.1:Solution of the well-posed problem given in Eq.(2.1.7),by MLPG mixed-2 collocation method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h is de fined as the radius of the support range associated with each node xI.

Figure 4.3.2:Solution of the ill-posed problem given in Eq.(2.1.9),by MLPG mixed-2 collocation method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h is de fined as the radius of the support range associated with each node xI.

Figure 4.3.3:Solution of the well-posed problem given in Eq.(2.1.7),by MLPG mixed-2 finite volume method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node

Figure 4.3.4:Solution of the ill-posed problem given in Eq.(2.1.9),by the MLPG mixed-2 finite volume method,with Moving Least Squares.15 uniformly distributed nodes are used to construct the MLS basis function.rI=3.5h and l=3.5h are de fined as the radius of the support range and subdomain associated with each node

And boundary conditioned can be enforced by collocation:

In Fig(4.3.1)-(4.3.4),the MLPG mixed-2 collocation and FVM methods based on MLS,is used to solve the well-posed and ill-posed problems.It can be clearly seen that,the accuracy of the current MLPG mixed-2 methods are the best among all the various MLPG methods,for both well-posed and ill-posed problems.This is due to the fact that only the first-order derivative is involved throughout the formulation.

5　Conclusion

A variety of computational methods is developed to solve a 4thorder ordinary differential equation(beam on an elastic foundation).These computational methods differ from each other,mainly due to:various primal or mixed formulations,various global or local,symmetric or unsymmetric weak-forms,various global or local interpolations of trial functions,and various test functions such Dirac delta,Heaviside,fundamental solution as well as other functions are employed.The objective of this study is not to find the best computational method,because each of them has its advantages&disadvantages.The objective of this study is to demonstrate that all the computational methods are essentially branches of the same tree.

However.some fundamental concepts of computational methods are given here:

1.Weak-forms can be written either globally or on a local subdomain.

2.Integrations by parts for the weak-forms can be used to reduce the continuity requirement of trial functions,with the price of increasing the continuity requirement of test functions.

3.Mixed formulations reduce the order of differentiation for each mixed variable,and thus reduce the requirement on the continuity of trial functions.However,mixed formulations do not increase the continuity requirement of test functions.

4.Global interpolations lead to fully-populated,ill-conditioned coefficient matrices,which increase the burden and difficulty of solving the system of algebra equations.

5.Element-based interpolations can hardly achieve high-order continuity,especially for high-dimensional problems.For those higher-order high-dimensional problems,it is natural to use mixed formulations.

6.Node-based meshless local interpolations can easily achieve higher-order continuity.But its higher-order derivatives are too complex to be useful.Thus,using mixed formulations greatly increase the accuracy of meshless methods.

7.Finite elements are unsuitable for solving inverse problems.This is because the symmetric weak-form cannot accommodate with ill-posed BCs.

8.Boundary elements reduce the trial solutions by one-dimension.However,its formulation is somehow more complex.

Acknowledgement:This work was funded by the Deanship of Scientific Research(DSR),King Abdulaziz University,under grant number(3-130-25-HiCi).The authors,therefore,acknow ledge the technical and financial support of KAU.This research is also supported in part by the Mechanics Section,Vehicle Technology Division,of the US Army Research Labs,under a collaborative research agreement with UCI.

Atluri,S.(2004):The meshless method(MLPG)for domain&BIE discretizations.Tech Science Press.

Atluri,S.(2005):Methods of computer modeling in engineering&the sciences.Tech Science Press.

Atluri,S.;Dong,L.(2015):Introduction to Computational Methods in Engineering.Tech Science Press.(to appear).

Atluri,S.N.;Han,Z.D.;Rajendran,A.M.(2004):A new implementation of the meshless finite volume method,through the mlpg"mixed"approach.CMES:Computer Modeling in Engineering&Sciences,vol.6,no.6,pp.491–514.

Atluri,S.N.;Han,Z.D.;Shen,S.P.(2003):Meshless local petrov-galerkin(m lpg)approaches for solving the weakly-singular traction&displacement boundary integral equations.CMES:Computer Modeling in Engineering&Sciences,vol.4,no.5,pp.507–518.

Atluri,S.N.;K im,H.G.;Cho,J.Y.(1999):A critical assessment of the truly meshless local petrov-galerkin(m lpg),and local boundary integral equation(lbie)methods.Computational mechanics,vol.24,pp.348–372.

Atluri,S.N.;Liu,H.T.;Han,Z.D.(2006):Meshless local petrov-galerkin(m lpg)mixed collocation method for elasticity problems.CMC:Computers,Materials&Continua,vol.14,no.3,pp.141–152.

Atluri,S.N.;Liu,H.T.;Han,Z.D.(2006):Meshless local petrov-galerkin(m lpg)mixed finite difference method for solid mechanics.CMES:Computer Modeling in Engineering&Sciences,vol.15,no.1,pp.1–16.

Atluri,S.N.;Shen,S.P.(2002):The meshless local Petrov-Galerkin(MLPG)method.Tech Science Press.

Atluri,S.N.;Shen,S.P.(2002):The meshless local petrov-galerkin(m lpg)method:a simple&less-costly alternative to the finite element and boundary element methods.CMES:Computer Modeling in Engineering&Sciences,vol.3,no.1,pp.11–51.

Atluri,S.N.;Shen,S.P.(2005):Simulation of a 4thorder ode:illustration of various primal&mixed mlpg methods.CMES:Computer Modeling in Engineering&Sciences,vol.7,no.3,pp.241–268.

Atluri,S.N.;Sladek,J.;Sladek,V.;Zhu,T.(2000):The local boundary integral equation(lbie)and it’s meshless implementation for linear elasticity.Computational mechanics,vol.25,pp.180–198.

Atluri,S.N.;Zhu,T.(1998):A new meshless local petrov-galerkin(mlpg)approach in computational mechanics.Computational mechanics,vol.22,pp.117–127.

Avila,R.;Han,Z.;Atluri,S.N.(2011):A novel mlpg- finite-volume mixed method for analyzing stokesian flows&study of a new vortex mixing flow.CMES:Computer Modeling in Engineering&Sciences,vol.71,no.4,pp.363–396.

Belytschko,T.;Lu,Y.Y.and Gu,L.(1994):Element-free galerkin methods.International journal for numerical methods in engineering,vol.37,pp.229–256.

Bishay,P.L.;Atluri,S.N.(2014):Trefftz-lekhnitskii grains(tlgs)for efficient direct numerical simulation(dns)of the micro/meso mechanics of porous piezoelectric materials.Computational Materials Science,vol.83,pp.235–249.

Cai,Y.C.;Paik,J.K.;Atluri,S.N.(2010):A triangular plate element with drilling degrees offreedom,for large rotation analyses of built-up plate/shell structures,based on the reissner variational principle and thevon karman nonlinear theory in theco-rotational reference frame.CMES:Computer Modeling in Engineering&Sciences,vol.61,no.3,pp.273–312.

Chen,J.T.;Wu,C.S.;Lee,Y.T.;Chen,K.H.(2007):On the equivalence of the trefftz method and method offundamental solutions for laplace and biharmonic equations.Computers&Mathematics with Applications,vol.53,pp.851–879.

Chen,W.;Fu,Z.;Chen,C.S.(2013):Recent Advances on Radial Basis Function Collocation Methods.Springer Berlin.

Cheung,Y.K.;Jin,W.G.;Zienkiew icz,O.C.(1991):Solution of helmholtz equation by trefftz method.International Journal for Numerical Methods in Engineering,vol.32,pp.63–78.

Dai,H.H.;Paik,J.K.;Atluri,S.N.(2011):The global nonlinear galerkin method for the analysis of elastic large deflections of plates under combined loads:A scalar homotopy method for the direct solution of nonlinear algebraic equations.CMC:Computers Materials and Continua,vol.23,no.69-99.

Dong,L.;Atluri,S.N.(2011):A simple procedure to develop efficient&stable hybrid/mixed elements,and voronoi cell finite elements for macro-µmechanics.CMC:Computers Materials&Continua,vol.24,no.1,pp.61–141.

Dong,L.;Atluri,S.N.(2012):Development of 3d t-trefftz voronoi cell finite elements with/without spherical voids&/or elastic/rigid inclusions for micromechanical modeling of heterogeneous materials.CMC:Computers Materials&Continua,vol.29,no.2,pp.169–211.

Dong,L.;Atluri,S.N.(2012):Development of 3d trefftz voronoi cells with ellipsoidal voids&/or elastic/rigid inclusions for micromechanical modeling of heterogeneous materials.CMC:Computers Materials&Continua,vol.30,no.1,pp.39–81.

Dong,L.;Atluri,S.N.(2012):Sgbem(using non-hyper-singular traction bie),and super elements,for non-collinear fatigue-grow th analyses of cracks in stiffened panels with composite-patch repairs.CMES:Computer Modeling in Engineering&Sciences,vol.89,no.5,pp.415–456.

Dong,L.;Atluri,S.N.(2012):A simple multi-source-point trefftz method for solving direct/inverse shm problems of plane elasticity in arbitrary multiply connected domains.CMES:Computer Modeling in Engineering&Sciences,vol.85,no.1,pp.1–43.

Dong,L.;Atluri,S.N.(2012):T-trefftz voronoi cell finite elements with elastic/rigid inclusions or voids for micromechanical analysis of composite and porous materials.CMES:Computer Modeling in Engineering&Sciences,vol.83,no.2,pp.183–219.

Dong,L.;Atluri,S.N.(2013):Fracture&fatigue analyses:Sgbem-fem or xfem?part 2:2d structures.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.2,pp.91–146.

Dong,L.;Atluri,S.N.(2013):Fracture&fatigue analyses:Sgbem-fem or xfem?part 2:3d solids.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.5,pp.379–413.

Dong,L.;Atluri,S.N.(2013):Sgbem voronoi cells(svcs),with embedded arbitrary-shaped inclusions,voids,and/or cracks,for micromechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua,vol.33,no.2,pp.111–154.

Han,Z.D.;Atluri,S.N.(2002):Sgbem(for cracked local subdomain)-fem(for uncracked global structure)alternating method for analyzing 3d surface cracks and their fatigue-grow th.CMES:Computer Modeling in Engineering&Sciences,vol.3,no.6,pp.699–716.

Han,Z.D.;Atluri,S.N.(2003):On simple formulations of weakly-singular traction&displacement bie,and their solutions through petrov-galerkin approaches.CMES:Computer Modeling in Engineering&Sciences,vol.4,no.1,pp.5–20.

Han,Z.D.;Liu,H.T.;Rajendran,A.M.;Atluri,S.N.(2006):The applications of meshless local petrov-galerkin(m lpg)approaches in high-speed impact,penetration and perforation problems.CMC:Computers Materials&Continua,vol.4,no.2,pp.119–128.

Han,Z.D.;Rajendran,A.M.;Atluri,S.N.(2005):Meshless local petrovgalerkin(m lpg)approaches for solving nonlinear problems with large deformations and rotations.CMES:Computer Modeling in Engineering&Sciences,vol.10,no.1,pp.1–12.

Kita,E.;Kamiya,N.(1995):Trefftz method:an overview.Advances in Engineering Software,vol.24,pp.3–12.

Lee,S.W.;Pian,T.H.H.(1978):Improvement of plate and shell finite elements by mixed formulations.AIAA journal,vol.16,pp.29–34.

Liu,C.S.(2008):A modified collocation trefftz method for the inverse cauchy problem of laplace equation.Engineering Analysis with Boundary Elements,vol.32,pp.778–785.

Okada,H.;Rajiyah,H.;Atluri,S.N.(1988):A novel displacement gradient boundary element method for elastic stress analysis with high accuracy.Journal of applied mechanics,vol.55,pp.786–794.

Okada,H.;Rajiyah,H.;Atluri,S.N.(1989):Non-hyper-singular integral representations for velocity(displacement)gradients in elastic/plastic solids(small or finite deformations).Computational mechanics,vol.4,pp.165–175.

Patankar,S.(1980):Numerical heat transfer and fluid flow.CRC Press.

Pluymers,B.;Van Hal,B.;Vandepitte,D.;Desmet,W.(2007):Trefftz-based methods for time-harmonic acoustics.Archives of Computational Methods in Engineeringa,vol.14,pp.343–381.

Qian,Z.Y.;Han,Z.D.;Atluri,S.N.(2013):A fast regularized boundary integral method for practical acoustic problems.CMES:Computer Modeling in Engineering&Sciences,vol.91,no.6,pp.463–484.

Sladek,J.;Sladek,V.;Atluri,S.N.(2000):Local boundary integral equation(lbie)method for solving problems of elasticity with nonhomogeneous material properties.Computational mechanics,vol.24,pp.456–462.

Sladek,J.;Sladek,V.;Zhang,C.(2003):Transient heat conduction analysis in functionally graded materials by the meshless local boundary integral equation method.Computational Materials Science,vol.28,pp.494–504.

Sladek,J.;Stanak,P.;Han,Z.D.;Sladek,V.;Atluri,S.N.(2013):Applications of the mlpg method in engineering&sciences:A review.CMES:Computer Modeling in Engineering&Sciences,vol.92,no.5,pp.423–475.

Spalding,D.B.(1972):A novel finite difference formulation for differential expressions involving both first and second derivatives.AIAA journal,vol.4,pp.551–559.

Trefftz,E.(1926):Ein gegenstück zum ritzschen verfahren.Proceedings of the second International Congress in Applied Mechanics,Zurich,pp.131–137.

Yeih,W.;Liu,C.S.;Kuo,C.L.;Atluri,S.N.(2010):On solving the direct/inverse cauchy problems of laplace equation in a multiply connected domain,using the generalized multiple-source-point boundary-collocation trefftz method&characteristic lengths.CMC:Computers,Materials&Continua,vol.17,no.3,pp.275–302.

Zhang,T.;Dong,L.;A lotaibi,A.;Atluri,S.N.(2013):Application of the mlpg mixed collocation method for solving inverse problems of linear isotropic/anisotropic elasticity with simply/multiply-connected domains.CMES:Computer Modeling in Engineering&Sciences,vol.94,no.1,pp.1–28.

Zhang,T.;He,Y.;Dong,L.;Li,S.;Alotaibi,A.;Atluri,S.N.(2014):Meshless local petrov-galerkin mixed collocation method for solving cauchy inverse problems of steady-state heat transfer.CMES:Computer Modeling in Engineering&Sciences,vol.97,no.6,pp.509–553.

Zhu,T.;Zhang,J.D.;Atluri,S.N.(1998):A local boundary integral equation(lbie)method in computational mechanics,and a meshless discretization approach.Computational mechanics,vol.21,pp.221–235.

Zhu,T.;Zhang,J.D.;Atluri,S.N.(1998):A meshless local boundary integral equation(lbie)method for solving nonlinear problems.Computational mechanics,vol.22,pp.174–186.

Zieli´nski,A.P.;Herrera,I.(1987):Trefftz method: fitting boundary conditions.International Journal for Numerical Methods in Engineering,vol.24,pp.871–891.

Zienkiew icz,O.C.;M orice,P.B.(1971):The finite element method in engineering science.London:M cGraw-hill.